1. Introduction
Turbocharging and boosting are key technologies in the continued drive for improved internal combustion engine efficiency with reduced emissions [
1]. For more than a decade, engine boosting has seen widespread adoption by passenger and heavy goods vehicle powertrains in order to increase the specific power and enable the downsizing megatrend [
2]. However, many challenges still remain, as the regulation requirements become stricter, and the demand for low-carbon powertrains increases [
3]. Currently, the growing expectations of vehicle performance, including an excellent transient response with high boost levels, have converged within the demand for increased downsizing and higher levels of EGR. For boosting machinery, the rated power and torque for downsized units are conventionally regained via fixed-geometry turbocharging [
4]. However, the transient behavior of such systems is limited by the usual requirement of a large size turbocharger, especially if a high-end torque is pursued [
5,
6]. VGT technology (see
Figure 1), which is designed to vary the effective aspect ratio of the turbocharger under different engine operating conditions [
7], can significantly improve an engine’s transient response and fuel economy compared with a fixed-geometry turbocharger [
8].
Due to the nonlinear characteristics of the VGT system and the fact that EGR and VGT systems are strongly interactive, the boost control of the VGT is recognized as a major challenge for diesel engines [
9]. Currently, the fixed-parameter gain-schedule PID control is used in the automotive industry for VGT boost control owing to its simplicity, robustness, and effectiveness [
10], but the control performance is sensitive to the state of the control loop, and is difficult to be satisfactory when the loop alters [
11,
12]. One of the feasible approaches to solve this problem is by proposing adaptive hybrid PID controllers. For example, in [
13], the fuzzy technique was combined with a PI controller, and a better control performance was demonstrated. In addition, Sant and Rajagopal proposed a hybrid control system that includes a steady-state PI controller and a transient fuzzy controller [
14]. However, both these approaches adopt offline-tuning rules, which are sensitive to system uncertainty. Another direction to improve the behavior of a PID controller is to replace it with a brand-new control structure. For example, an online self-learning deep deterministic policy gradient (DDPG) algorithm was employed for the boost control of a VGT-equipped engine. Although the proposed strategy can develop good transient control behavior by direct interaction with its environment, it takes much time for the algorithm to learn from no experience, and it is hardly possible to train the algorithm directly on a real plant due to its random exploration when a control strategy has to be learned from scratch [
15].
Reinforcement learning (RL), being as one of three machine learning paradigms, along with supervised learning and unsupervised learning, is the field of machine learning focusing on how control actions are selected in the environment in an optimal manner by trial and error [
16,
17]. The theory of reinforcement learning, inspired by the psychology of behaviorism, focuses on online learning and tries to maintain a balance between exploration and exploitation [
18]. Different from supervised learning and unsupervised learning, reinforcement learning does not require any pre-given data, but obtains learning information and updates model parameters by receiving rewards (feedback) from the environment for actions [
19,
20,
21]. Deep reinforcement learning (DRL), which excels at solving a wide variety of Atari and board games, is an area of machine learning that combines the deep learning approach and reinforcement learning (RL) [
22,
23]. The deep Q-network (DQN) strategy adopted on AlphaGo [
24] and AlphaGo Zero [
25] formed the first computer program that defeated human experts at the game of Go. It effectively solves the problem of instability and divergence caused by the use of neural network nonlinear value approximators through experience replay and fixed Q-Target, which greatly improves the applicability of reinforcement learning. Recently, Wang et al. [
26] updated DQN by proposing an architecture that consists of dueling networks. Their dueling networks replace the state-action value by two separate estimators: one for state-value function, and the other for state-dependent advantage function. This is particularly beneficial if a control action does not have any influence on the environment in any situation. By doing so, their RL agent proved superior to the latest technologies in the Atari 2600 domain. However, the aforementioned model-free DRL algorithms typically require a very large number of random exploration before achieving a good control performance; thus, it is hardly possible to apply the algorithm directly on a real plant, and have to rely heavily on a simulation environment, especially when a control strategy has to be learned from scratch. In contrast, the traditional PID method can control a process from its beginning to its end, and deliver a complete function solution without needing to procure anything from a third party (i.e., the concept of end-to-end); therefore, it can be easily implemented on real controllers without relying on simulation models. Based on the discussion above and that there exists no simulation model at many times for the training of a pure DRL strategy, it is interesting to combine a traditional PID controller and an intelligent DRL strategy together in order to realize an end-to-end control using the latest DRL achievement in a real environment.
In the following paper, a hybrid end-to-end control strategy combining an intelligent dueling deep Q-network and traditional PID for the transient boost control of a diesel engine with a variable geometry turbocharger and cooled EGR will be proposed. The remaining of this article is structured as follows: In
Section 2, the hybrid control framework is proposed to realize an optimal boost control of a VGT-equipped engine. In
Section 3, a comparison between the proposed end-to-end hybrid algorithm, a classical model-free DRL algorithm, and a fine-tuned PID controller are conducted and discussed.
Section 4 concludes the article.
2. Hybrid Control Framework
In this section, firstly, the mean value model of the research engine is introduced. After that, the implementation mechanism of the dueling DQN and the corresponding testing platform are described. Finally, the proposed adaptive hybrid control strategy combining intelligent DQN and traditional PID is elaborated.
2.1. Engine Model Analysis
In this article, the boost control strategy is implemented on a six-cylinder, three-liter VGT-equipped diesel engine, which can be seen in
Figure 2. A detailed engine model has been converted to a mean value model in order to reduce the run time without sacrificing transient accuracy [
27] (see Ref. [
15] for detailed explanation). Note that the mean value GT-Suite model (see
Figure 3) serves as a “real” engine environment in this study, so as to show the results between the end-to-end and non-end-to-end model-free approaches, but the proposed method can be transferred to a real plant easily. In order to provide a comparison, the model is initially controlled by a fine-tuned PID controller.
2.2. Dueling Deep Q-Network Architecture
Reinforcement learning is a computational approach to learning whereby an agent tries to maximize the total amount of reward it receives when interacting with environment (see
Figure 4) [
28,
29]. For every state
, the agents always try to maximize the expected discounted return by choosing an action
. The discounted return is defined as
, where
is a discount factor and
stands for the reward that is observed by the agent after an action is exerted on the environment.
For an agent behaving according to a policy π, the state-action function and the state function are defined as follows:
and:
The value function described above is a high-dimensional object. For approximation, a deep Q-network
with parameter
can be used, and the following loss function sequence is optimized at iteration
:
In order to solve the problem of instability and divergence caused by the use of nonlinear value approximators, the classical DQN algorithm adopted the strategy of experience replay and fixed Q-target, which are considered as two key factors in its great success on Alpha Go. The following shows the algorithm pseudo-code of the proposed DQN algorithm for the boost control problem in this study.
| DQN Algorithm: |
| Initialize replay memory to capacity |
| Initialize action-value function with random weights |
| Initialize target action-value function with weights |
| For episode = 1, M do |
| Initialize sequence |
| For t= l, T do |
| With probability s select a random action |
| otherwise select |
| Execute action in emulator and observe reward and image |
| Set |
| Store transition in |
| Sample random minibatch of transitions from D |
| Set |
| Perform a gradient descent step on with respect to the |
| network parameters |
| Every steps reset |
| End For |
| End For |
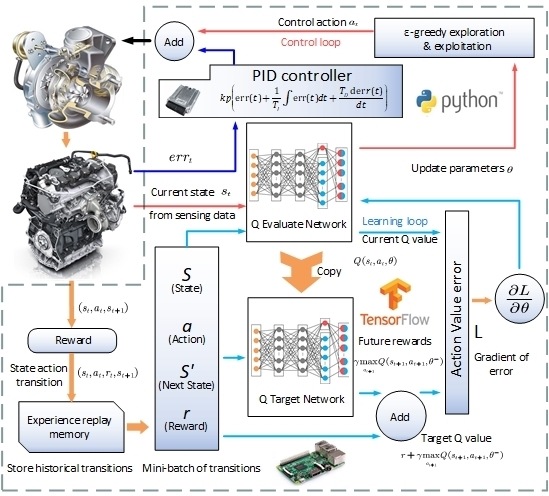
The updated dueling DQN algorithm implementation and the corresponding testing platform are illustrated in
Figure 5. Unlike the classical DQN, which only produces a single output Q function, the dueling DQN use two streams of fully connected layers to provide the estimate of the state and the advantage functions before combining them to generate output Q functions. By separating the state value function from the Q function, the updated dueling DQN is capable of solving control problems whose estimate of the state values is of great importance, while for many circumstances, the choice of actions does not have any influence on the environment. The vane position controlled by a membrane vacuum actuator is selected for the control action, and the four quantities of engine speed, actual boost pressure, target boost pressure, and current vane position are used to group the four-dimensional state space. For the choice of immediate reward (
), the function of the error between the target boost and the current boost (
) plus the action change rate (
is defined, and the specific formula is as follows:
The dueling Q-network illustration and the parameters of the proposed dueling DQN can be seen from
Figure 6 and
Table 1. In this study, the input layer of the dueling Q-network has five states, and there are two hidden layers each having 80 neurons, respectively. Before acquiring the Q function at the output layer, two streams that independently estimate the state functions and the advantages functions are constructed. It should be noted here that the hyper parameters are only using standard values without fine tuning. Although in theory the control performance could be further improved, this is out of the scope of this research, as the objective of this paper is only to introduce another intelligent control frame to track the boost pressure for a VGT-equipped diesel engine. The training dataset is composed of 50 data episodes, and each episode represents the data for the first 1098s of the FTP-72 trips.
2.3. Adaptive Hybrid Control System Combining Intelligent Dueling DQN and Traditional PID
Most of the control processes in the industry adopt the PID controller currently due to its simple structure and robust performance under complex conditions. However, the fixed-parameter structure makes it degraded when the control loop alters. Meanwhile, the DRL algorithm can self-learn a good control behavior by direct interaction with the environment. Therefore, it is interesting to establish a hybrid algorithm that combines the intelligent DRL (for example, the aforementioned dueling DQN) algorithm and a traditional PID controller, in order to take advantage of DRL’s self-learning capability to tune a PID performance online. Unlike the practice proposed by some literatures [
16,
30], which uses the reinforcement learning approach to adjust the gains of PID controllers, in this paper, a simpler but more powerful method will be introduced by adding a dueling DQN algorithm directly after a fine-tuned PID controller, as can be seen in
Figure 7. There are two special modifications that need to be considered here. First, the action range of the dueling DQN is limited, and for paper simplicity, this will be elaborated later. Second, another state—i.e., the PID action output—will be imported to the aforementioned dueling DQN algorithm. This is a practice to allow the dueling DQN strategy to learn the system behavior controlled by an existing PID controller.
This approach will intuitively enable a reasonable learning curve, as the proposed dueling DQN only needs to adjust an already fine-tuned PID output. However, the most innovative aspect of this practice is allowing the training process of the DRL algorithm to be performed directly for a real plant. It is known that ‘conventional’ DRL algorithms require a large number of random explorations especially at the beginning of the training and this, for most real plants, is not allowed, as poor action behaviors could cause damage to or even destroy the plants. Thus, for most RL study, a large part of the training (especially for the beginning) can only be carried out in a simulation environment. Depending on the fidelity of the simulation model, the control strategy obtained from the simulation may need to continue learning with the real environment. Although this method combines the simulation training and the experimental continuing training together in order to fully utilize the computational resources offline and refine the algorithm in the experimental environment online, a simulation model with relatively high fidelity is required. Thus, this approach is not ‘model-free’ in the strict sense. By combining both an intelligent dueling DQN and a traditional PID, this hybrid control approach, innovatively allowing the training process of the DRL algorithm that previously could only be carried out in the simulation environment, can now be performed directly on a real plant. This is realized by giving the control strategy some ‘guided experience’ before learning through making use of an existing fine-tuned PID controller and then allowing DRL control actions to autonomously learn the interaction with the real environment in order to further improve the control performance, based on a relatively good benchmark. With the help of the PID controller offering a good baseline, the combined control action will oscillate decently, even at the beginning of training, without violating real plant safety limit and not affecting the exploration performance of the algorithm. This approach, to the best of the authors’ knowledge, will be the first attempt that is able to apply the DRL directly on a real plant, which in a sense achieves the real ‘model-free’ control.
3. Results and Discussion
The presented hybrid end-to-end control strategy is validated in this section. In order to mimic real-world driving behavior, the target boost pressure of the engine under a US FTP-72 (Federal Test Procedure 72) driving cycle was selected as the control objective, and the first 80% of this dataset is used to train the learning algorithm with the remaining for testing analysis. A comparative analysis of the tracking performance between a benchmark PID controller, a classical model-free DRL algorithm, and the dueling DQN + PID algorithm is performed to verify the advantage of the proposed method. First, the control performance with a fine-tuned gain-schedule PID controller is shown. Second, the learning curve of a classic model-free DRL algorithm and the proposed algorithm is discussed, and the boost tracking performance at the very first training episode for both algorithms is compared. Finally, the control performance of the proposed algorithm is demonstrated to achieve a high level of control performance, generality, and adaptiveness when compared with the aforementioned PID benchmark. For the whole section, one of the commonly used control performance measures—i.e., IAE—is adopted to compare each control algorithm.
The fine-tuned PID control behavior can be seen in
Figure 8. The control parameters in this PID controller are tuned by the classic Ziegler–Nichols method, which takes a lot of effort; however, its performance can be recognized as a good control benchmark. It should be noted that the emphasis in this research is to propose a practical learning structure that allows the control strategy to learn the interactions with a real transient environment directly (without relying on a simulation model) and finally form a good control behavior. Thus, a conclusion of which algorithm is better than the other cannot be drawn (especially when the driving cycle is known), as it is believed that the control behavior largely depends on the efforts of tuning.
The learning curve that shows the cumulated rewards of each episode for the hybrid algorithm, the DDPG algorithm, and the benchmark PID controller can be seen from
Figure 9. The trajectory of the DDPG algorithm (which has been published in [
15]) illustrates a classical learning process from scratch using model-free DRL algorithms. It is shown that from the beginning of the training that the accumulated rewards for the DDPG agent per episode are extremely low, indicating poor control behavior, and after approximately 40 episodes, the accumulated rewards can be converged slowly to a higher value than that of the benchmark fine-tuned PID controller, indicating a preferable control performance. However, this approach cannot be directly applied on a real plant due to the possible plant damage resulting from its random and not wise control action when the agent has limited experience, especially at the beginning of the training. However, the proposed hybrid algorithm is distinct from the DDPG learning curve by offering the control strategy a good action baseline, making it practicable to train the algorithm directly on a real plant.
To make it clearer, the control behaviors of the DDPG and the hybrid algorithm at the very first training episode are shown in
Figure 10. It is shown that the boost pressure of the DDPG algorithm is far away from the target, and due to its random control action (so as to realize extensive exploration), the boost pressure easily exceeds the safety margin. This may be forgiven in the simulation environment, but will most likely damage a real plant in one attempt, not to mention that this kind of model-free DRL algorithm requires a very large number of random actions to achieve good performance. However, for the proposed hybrid algorithm, the boost tracking performance at the very first episode is acceptable, and the boost pressure is well below the safety margin. This is because (1) the action range of the dueling DQN is limited; and (2) the PID acts as a compensator to modify the incorrect action implemented by the dueling DQN at the very first episode. Note that only after approximately five episodes, the hybrid algorithm has already been converged, and the accumulated rewards are basically the same as those achieved by the DDPG algorithm requiring nearly 50 episodes, indicating a superior computational efficiency.
Figure 11 shows the control behavior of the proposed hybrid algorithm, and when it is compared with
Figure 8, it can be seen that the control behavior based on the proposed hybrid algorithm outperforms that of the PID controller, with the IAE for each being 40.12 and 31.83, respectively.
In order to show the generalization ability of the proposed hybrid algorithm, as indicated in
Figure 12, the control behavior comparison between the fine-tuned PID and the proposed hybrid algorithm using testing dataset is conducted. Compared with the results of the fine-tuned PID controller (the parameters of the PID controller were initially optimized for the whole period of the FTP-72 driving cycle), the average control behavior based on the proposed algorithm performs marginally better, as indicated by the IAE of the PID being 9.84 and that of the proposed algorithm being 8.89. However, the actual boost pressure of the proposed algorithm suffers a high-frequency oscillation compared with the PID benchmark. In order to test its adaptivity, a continuous learning is implemented using a long driving cycle containing this specific driving cycle. After a short time, as shown in
Figure 13, the agent is able to follow the target boost better, and the oscillation is almost eliminated, showing the superior adaptiveness of this hybrid algorithm.
Furthermore, by adding another redundant control module, this hybrid method can also improve the system’s reliability. This redundancy, unlike most of the other literature, is achieved by enabling DRL algorithms to adapt themselves to the behavior of the system under different PID outputs while trying to maximize the cumulative rewards. This will not only help improve the control behavior when the PID controller behaves decently, but also provide a satisfactory control correction when the PID controller functions abnormally or a total failure occurs. For example, under minor PID issues, the dueling DQN is able to adjust the control parameters autonomously by direct interaction with the environment (thus, a well-behaved controller can be re-developed).
Figure 14 simulates this phenomenon by adding a random noise to the PID controller. It is shown that the hybrid algorithm behaves decently well, while the benchmarking PID controller suffers pressure oscillation. For bigger problems, this hybrid architecture can also output a relatively good control behavior, which will help keep the power within the reasonable ranges for the control case of boosted internal combustion engines. This is done by introducing a simple switch in the hybrid controller. To be more specific, when a PID controller failure occurs, a constant value of 0.5 in our study rather than 1 (which is the current industrial practice to protect the engine) is sent to the dueling DQN controller, as can be seen in
Figure 7. Without requiring re-learning with the environment (see
Figure 15), a good control behavior can still be realized, and it’s much better than that of the PID benchmark, whose pressure is well below the target, indicating a lack of power.