A Dual-Vector Modulated Model Predictive Control Method for Voltage Source Inverters with a New Duty Cycle Calculation Method

Abstract

Recently, model predictive control (MPC) methods have been widely used to achieve the control of two-level voltage source inverters due to their superiorities. However, only one of the eight basic voltage vectors is applied in every control cycle in the conventional MPC system, resulting in large current ripples and distortions. To address this issue, a dual-vector modulated MPC method is presented, where two voltage vectors are selected and utilized to control the voltage source inverter in every control cycle. The duty cycle of each voltage vector is figured out according to the hypothesis that it is inversely proportional to the square root of its corresponding cost function value, which is the first contribution of this paper. The effectiveness of this assumption is verified for the first time by a detailed theoretical analysis shown in this paper based on the geometrical relationship of the voltage vectors, which is another contribution of this paper. Moreover, further theoretical analysis shows that the proposed dual-vector modulated MPC method can also be extended to control other types of inverters, such as three-phase four-switch inverters. Detailed experimental results validate the effectiveness of the presented strategy.

1. Introduction

Due to the advantages of two-level voltage source inverters, they have received more and more attention in the field of renewable energy generation systems, including photovoltaic systems and energy storage systems, among others. Recently, the control methods of two-level voltage source inverters have been widely studied to achieve smooth and flexible energy conversion [1,2,3,4,5]. As is known, vector control is widely used to control two-level voltage source inverters in renewable energy generation systems as it can achieve power decoupling control. Nevertheless, proportional and integral controller and pulse width modulation modules are needed, which makes the control system hard to debug and prolongs the development cycle of the control system. Another control method, i.e., direct power control, has also been studied to control two-level voltage source inverters. Compared to vector control, proportional and integral controller and pulse width modulation modules are removed. However, as the switching frequency is unfixed and the optimal voltage vector is selected based on an offline switch table, its power control precision is relatively low.

As a simple but effective control method, model predictive control (MPC) has received much more attention in the field of the optimal control of two-level voltage source inverters lately.

An MPC strategy was designed to control the current of two-level voltage source inverters in [6] in 2007. From then on, many researchers began to study new MPC strategies to reduce the computational time [7,8], to lower the switching frequency [9,10], to suppress the common-mode voltage [11,12], to decrease the current ripples [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29], or to minimize the power ripples [30,31,32].

In [7,8], according to the deadbeat control principle, voltage-based cost functions are designed to replace the conventional current-based cost function. Thus, the calculation burden is reduced significantly. In [9,10], the concept of multistep MPC is studied and evaluated, which can reduce the switching frequency obviously, making it very suitable for large power converters. In [11,12], common-mode voltage suppression methods are studied using an MPC strategy. Thus, the negative effects of the common-mode voltage are reduced.

Additionally, as a flexible control method, MPC strategies are also studied in [13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29] to reduce the current ripples by using more voltage vectors instead of only one in every control cycle. In [13,14,15], dual-vector MPC strategies are studied. Compared to the conventional single-vector MPC, the control precision is improved as more voltage vectors are utilized in every control cycle. Moreover, in [16,17,18,19,20,21], three voltage vectors are chosen per control cycle to further enhance the control performance, and better results are obtained. In these methods in [13,14,15,16,17,18,19,20,21], the duty cycles of each voltage vector are figured out according to the deadbeat control theory. Although duty cycles can be calculated accurately theoretically, the actual calculated duty cycle may be smaller than zero or larger than one, which reduces the control performance to a certain extent.

Alternately, there is another way to determine the duty cycles, which is named modulated MPC [22,23,24,25,26,27,28,29]. In this type of method, the duty cycle of each voltage vector is deduced by assuming that it is inversely proportional to its cost function value. As it is simple but effective, many researchers have studied modulated MPC to control the cascaded H-bridge converter [22], the multilevel solid-state transformer [23], the direct and indirect matrix converter [24,25], the shunt active filter [26], the brushless doubly fed induction machine [27], the two-level three-phase inverter [28,29], and so on. However, although it is shown in [22,23,24,25,26,27,28,29] that the modulated MPC method can achieve current control, up to now, there still lacks a solid theoretical support for this kind of method, which hinders its popularization and application.

Additionally, to minimize the power ripples of the converters, modified MPC strategies have also been studied in [26,30,31,32]. However, there are still few papers to study the optimal modulated model predictive direct power control methods as well as the theoretical analysis for power converters.

To fill this gap, a novelty dual-vector modulated MPC strategy is presented for two-level voltage source inverters with a new duty cycle calculation method as well as a detailed theoretical analysis. First, twelve hybrid voltage vectors are constructed according to the eight basic voltage vectors of the two-level voltage source inverter. Next, to decrease the computation amount, the reference voltage is deduced based on the reference current, and a cost function based on the voltage error is designed. Then, only three hybrid voltage vectors are required to be evaluated online per control period based on the information of the reference voltage. Finally, the optimal voltage vector combination is selected.

The main contributions of this paper lie in three aspects.

The first one is that a new duty cycle calculation method of each voltage vector is proposed in this paper according to the hypothesis that it is inversely proportional to the square root of its cost function value.

The next one is that, based on a detailed theoretical analysis, the validity of the presented dual-vector modulated MPC strategy with the new duty cycle calculation method is proved based on the geometrical relationship of the voltage vectors, which is also verified by experimental results.

The third one is that the proposed dual-vector modulated MPC strategy can also be applied to control other types of inverters, such as three-phase four-switch inverters, whose effectiveness is also proved by the geometrical relationship of the voltage vectors as well as the experimental results.

2. Conventional MPC Strategy

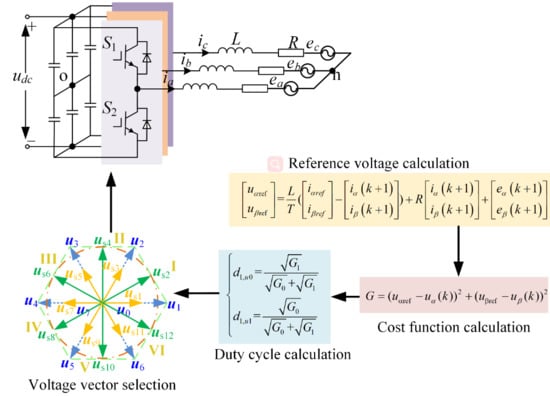
Figure 1 depicts the topology of two-level voltage source inverters. As is known, there are eight voltage vectors for two-level voltage source inverters, including u₀(000), u₁(100), u₂(110), u₃(010), u₄(011), u₅(001), u₆(101), and u₇(111), which are shown in Figure 2.

Typically, (1) shows the mathematical equation of two-level voltage source inverters on the α-β reference.

$$L\frac{d}{dt}\left[\begin{array}{l}{i}_{\alpha }\\ i_{\beta }\end{array}\right]=\left[\begin{array}{l}{u}_{\alpha }\\ u_{\beta }\end{array}\right]-R\left[\begin{array}{l}{i}_{\alpha }\\ i_{\beta }\end{array}\right]-\left[\begin{array}{l}{e}_{\alpha }\\ e_{\beta }\end{array}\right]$$

(1)

where u_α, u_β and i_α, i_β are the output AC voltages and currents, respectively, and e_α and e_β are the back electromotive forces (EMFs). L stands for the filter inductance with R denoting the parasitic resistance on it.

If the sample and control cycle is T, based on the Euler’s discretization formula, it can be calculated that

$$\frac{L}{T}\left[\begin{array}{l}{i}_{\alpha }\left(k+1\right)-i_{\alpha }\left(k\right)\\ i_{\beta }\left(k+1\right)-i_{\beta }\left(k\right)\end{array}\right]=\left[\begin{array}{l}{u}_{\alpha }\left(k\right)\\ u_{\beta }\left(k\right)\end{array}\right]-R\left[\begin{array}{l}{i}_{\alpha }\left(k\right)\\ i_{\beta }\left(k\right)\end{array}\right]-\left[\begin{array}{l}{e}_{\alpha }\left(k\right)\\ e_{\beta }\left(k\right)\end{array}\right]$$

(2)

Based on (2), as well as the sampled current i_α(k) and i_β(k) at the kth instant, the current i_α(k + 1) and i_β(k + 1) at the next control cycle can be calculated, as depicted in (3).

$$\left[\begin{array}{l}{i}_{\alpha }\left(k+1\right)\\ i_{\beta }\left(k+1\right)\end{array}\right]=\left(1-\frac{RT}{L}\right)\left[\begin{array}{l}{i}_{\alpha }\left(k\right)\\ i_{\beta }\left(k\right)\end{array}\right]+\frac{T}{L}\left[\begin{array}{l}{u}_{\alpha }\left(k\right)-e_{\alpha }\left(k\right)\\ u_{\beta }\left(k\right)-e_{\beta }\left(k\right)\end{array}\right]$$

(3)

As there is an inherent one-step delay in the MPC system, to reduce its influences, it can be compensated by using the optimal voltage vector selected in the last control period to predict the current i_α(k + 1) and i_β(k + 1) firstly. Next, the eight basic voltage vectors u_k+1 = [u_α(k + 1), u_β(k + 1)]^T can be further utilized to calculate the current i_α(k + 2) and i_β(k + 2) based on (4).

$$\left[\begin{array}{l}{i}_{\alpha }\left(k+2\right)\\ i_{\beta }\left(k+2\right)\end{array}\right]=\left(1-\frac{RT}{L}\right)\left[\begin{array}{l}{i}_{\alpha }\left(k+1\right)\\ i_{\beta }\left(k+1\right)\end{array}\right]+\frac{T}{L}\left[\begin{array}{l}{u}_{\alpha }\left(k+1\right)-e_{\alpha }\left(k+1\right)\\ u_{\beta }\left(k+1\right)-e_{\beta }\left(k+1\right)\end{array}\right]$$

(4)

Finally, by evaluating the prediction errors of all the eight basic voltage vectors using the cost function defined in (5), an optimal voltage vector can be chosen and utilized to control the inverter during the next control cycle.

$$g={(i_{\alpha \mathrm{ref}}-i_{\alpha }(k+2))}^2+{(i_{\beta \mathrm{ref}}-i_{\beta }(k+2))}^2$$

(5)

where i_αref and i_βref are the reference currents.

As only one voltage vector is utilized in every control cycle in the above conventional MPC strategy, the current total harmonic distortion (THD) is quite large.

Aiming to solve this problem, a dual-vector modulated MPC strategy is presented in this paper by using two voltage vectors in every control cycle. Detailed theoretical analysis is carried out to verify the validity of the presented dual-vector modulated MPC strategy. Comparative experimental results also verified its effectiveness.

3. Dual-Vector Modulated MPC Strategy

According to [7,8], to simplify the MPC strategy, a cost function based on the reference voltage is defined in this paper.

First, the reference voltage is deduced according to the deadbeat control theory, which is shown in (6).

$$\left[\begin{array}{l}{u}_{\alpha \mathrm{ref}}\\ u_{\beta \mathrm{ref}}\end{array}\right]=R\left[\begin{array}{l}{i}_{\alpha }\left(k+1\right)\\ i_{\beta }\left(k+1\right)\end{array}\right]+\left[\begin{array}{l}{e}_{\alpha }\left(k+1\right)\\ e_{\beta }\left(k+1\right)\end{array}\right]+\frac{L}{T}(\left[\begin{array}{l}{i}_{\alpha ref}\\ i_{\beta ref}\end{array}\right]-\left[\begin{array}{l}{i}_{\alpha }\left(k+1\right)\\ i_{\beta }\left(k+1\right)\end{array}\right])$$

(6)

where u_αref and u_βref are the reference voltages.

To limit the voltage within the linear modulation region, if $u_m=\sqrt{u_{\alpha \mathrm{ref}}^2+u_{\beta \mathrm{ref}}^2}>u_{dc}/\sqrt{3}$, u_αref and u_βref are calculated based on (7).

$$\{\begin{array}{l}{u}_{\alpha \mathrm{ref}}=\frac{u_{\alpha \mathrm{ref}}}{u_m}\frac{u_{dc}}{\sqrt{3}}\\ u_{\beta \mathrm{ref}}=\frac{u_{\beta \mathrm{ref}}}{u_m}\frac{u_{dc}}{\sqrt{3}}\end{array}$$

(7)

Then, a voltage-based cost function is defined as

$$G={(u_{\alpha \mathrm{ref}}-u_{\alpha }(k))}^2+{(u_{\beta \mathrm{ref}}-u_{\beta }(k))}^2$$

(8)

Through using this voltage-based cost function, the calculation burden can be reduced as the prediction of the current for many times in each control cycle is not required any more.

To select and apply two voltage vectors per control period, twelve hybrid voltage vectors are constructed according to the eight basic voltage vectors of the two-level voltage source inverter. They are u_s1(u₀, u₁), u_s2(u₁, u₂), u_s3(u₇, u₂), u_s4(u₂, u₃), u_s5(u₀, u₃), u_s6(u₃, u₄), u_s7(u₇, u₄), u_s8(u₄, u₅), u_s9(u₀, u₅), u_s10(u₅, u₆), u_s11(u₇, u₆), and u_s12(u₆, u₁), respectively, which are illustrated in Figure 3.

The relationship between the twelve constructed hybrid voltage vectors and the basic voltage vectors is depicted in (9).

$${\mathit{u}}_{\mathrm{s}i}=d_{i,uj}{\mathit{u}}_j+d_{i,uk}{\mathit{u}}_k$$

(9)

where d_i,uj + d_i,uk = 1, d_i,uj is the duty cycle of u_j and d_i,uk is the duty cycle of u_k.

For example, as u_s1 is combined by u₀ and u₁, their relationship can be expressed as

$${\mathit{u}}_{\mathrm{s}1}=d_{1,u0}{\mathit{u}}_0+d_{1,u1}{\mathit{u}}_1$$

(10)

To calculate the values of the twelve constructed hybrid voltage vectors, the duty cycles of the basic voltage vectors should be calculated first. Different from the methods in [22,23,24,25,26,27,28,29], which lack theoretical support, here a new duty cycle calculation method is proposed by assuming that it is inversely proportional to the square root of its cost function value, as shown in (11), where m is a positive coefficient. In Section 4, the effectiveness of this proposed hypothesis is verified in detail by a particular theoretical analysis.

$$d_i=\frac{m}{\sqrt{G_i}}$$

(11)

Based on (9) and (11), the duty cycles of the basic voltage vectors are deduced. For instance, the duty cycles of u₀ and u₁ that construct u_s1 can be calculated based on (12).

$$\{\begin{array}{l}{d}_{1,u0}=\frac{\sqrt{G_1}}{\sqrt{G_0}+\sqrt{G_1}}\\ d_{1,u1}=\frac{\sqrt{G_0}}{\sqrt{G_0}+\sqrt{G_1}}\end{array}$$

(12)

where G₀ and G₁ are the values of the cost function shown in (8), which are obtained by substituting u₀ and u₁ into (8), respectively.

Finally, based on (9)–(12), the combined voltage vectors are figured out.

To simplify the predictive control, the voltage vector plane can be divided into six sectors, as illustrated in Figure 3. Then, according to the reference voltage shown in (6) and (7), its location can be obtained easily based on

Table 1. Sectors of the reference voltage.

Symbol	Angle Range	Sector
θ	[0, 60°)	I
	[60°, 120°)	II
	[120°, 180°)	III
	[180°, 240°)	IV
	[240°, 300°)	V
	[300°, 360°)	VI

, where θ = arctan(u_βref/u_αref).

Based on the position of the reference voltage, the alternative voltage vectors that should be evaluated online can be preselected based on

Table 2. Voltage vector selection method.

Sector of the Reference Voltage	Selected Voltage Vectors
I	us1, us2, and us3
II	us3, us4, and us5
III	us5, us6, and us7
IV	us7, us8, and us9
V	us9, us10, and us11
VI	us11, us12, and us1

. For instance, if the reference voltage is located at sector I, only u_s1, u_s2, and u_s3 require to be evaluated online. So, as only three instead of twelve voltage vectors are required to be evaluated online, the calculation amount is reduced notably. Then, an optimal hybrid voltage vector among the three hybrid voltage vectors can be chosen to control the inverter in the next control cycle.

For clarity, Figure 4 is given to show the control principle of the presented strategy. Moreover, the detailed implementation steps are also depicted below.

Step 1: Calculate the reference voltage based on (6) and (7);

Step 2: Get the values of the reference voltage based on Table 1;

Step 3: Choose three candidate voltage vectors based on Table 2;

Step 4: Figure out the duty cycles of the basic voltage vectors that construct the three candidate voltage vectors based on (8) and (12);

Step 5: Get the values of the three candidate voltage vectors based on (9);

Step 6: Evaluate the cost function values of the three candidate voltage vectors based on (8) and select the voltage vector that can minimize the cost function as the optimal one.

Finally, the optimal vector is utilized to control the voltage source inverter.

4. Theoretical Analysis of the Proposed Method

To validate the correctness of the presented duty cycle calculation method shown in (11), a rigorous theoretical analysis is proposed. Here, the case that the reference voltage vector is located at sector I is taken as an example, where it overlaps with the segment OD in Figure 5.

As u_s1 is constructed by u₀ and u₁, their relationship has been shown in (10). Based on (10), (13) can be deduced.

$$\begin{array}{l}{\mathit{u}}_{\mathrm{s}1}={\mathit{u}}_0+d_{1,u1}({\mathit{u}}_1-{\mathit{u}}_0)\\ \begin{array}{cc}& =\end{array}{\mathit{u}}_1+d_{1,u0}({\mathit{u}}_0-{\mathit{u}}_1)\end{array}$$

(13)

Based on (13) and Figure 5(a), it can be known that |OA| = d_1,u1*|u₁ − u₀| and |AB| = d_1,u0*|u₁ − u₀|. Thus, |OA|/|AB| = d_1,u1/d_1,u0. According to (11) and (12), it can be deduced that

$$\frac{d_{1,u1}}{d_{1,u0}}=\frac{\sqrt{G_0}}{\sqrt{G_1}}$$

(14)

According to the cost function shown in (8), it can be known that

$$\{\begin{array}{l}{G}_0={\left|\mathrm{OD}\right|}^2\\ G_1={\left|\mathrm{BD}\right|}^2\end{array}$$

(15)

Thus, it can be deduced that

$$\frac{\left|\mathrm{OA}\right|}{\left|\mathrm{AB}\right|}=\frac{\left|\mathrm{OD}\right|}{\left|\mathrm{DB}\right|}$$

(16)

By rearranging (16) with the law of sines in consideration, it can be further deduced that

$$\frac{\sin \angle \mathrm{ODA}}{\sin \angle \mathrm{OAD}}=\frac{\left|\mathrm{OA}\right|}{\left|\mathrm{OD}\right|}=\frac{\left|\mathrm{AB}\right|}{\left|\mathrm{DB}\right|}=\frac{\sin \angle \mathrm{ADB}}{\sin \angle \mathrm{DAB}}$$

(17)

Considering that ∠OAD + ∠DAB = π, it can be known that

$$\sin \angle \mathrm{OAD}=\sin \angle \mathrm{DAB}$$

(18)

Thus, (19) is finally deduced based on (17) and (18).

$$\sin \angle \mathrm{ODA}=\sin \angle \mathrm{ADB}$$

(19)

Based on (19), it can be calculated that ∠ODA + ∠ADB = π or ∠ODA = ∠ADB. In the following, both of the two cases are analyzed respectively.

First, if ∠ODA + ∠ADB = π is true, it can be calculated that point D must be located on the segment OB. In this situation, it can be figured out based on (16) that point D and point A will be the same point. That means u_s1 = u_αβref is true. Thus, the current control error can be minimized under this condition, which shows the validity of the duty cycle calculation algorithm proposed in this article.

Second, if point D is not located on the segment OB, ∠ODA = ∠ADB should be true. In this situation, it can be obtained that ∠ODA = ∠ADB < ∠OAD as ∠OAD = ∠ADB + ∠DBA. As ∠DOA < π/3 is true, and ∠ODA + ∠OAD + ∠DOA = π, it can be deduced that ∠ODA + ∠OAD >2π/3. As ∠OAD is larger than ∠ODA, ∠OAD > π/3 > ∠ODA can be deduced. As ∠DOA < π/3 and ∠OAD > π/3 are true, it can be known that ∠OAD > ∠DOA. According to the law of sines, |OD| > |AD| is finally deduced. As |AD| stands for the square root value of the cost function of u_s1, and |OD| denotes the square root value of the cost function of u₀, a conclusion is obtained, i.e., the control accuracy is increased when u_s1 is utilized to replace u₀.

Similarly, it is easy to verify that |DB| > |AD| is true, which means the control accuracy of u_s1 is increased compared to that of u₁. Moreover, based on Figure 5b,c, it can also be verified that the control error can be reduced by using u_s2 or u_s3 instead of u₀, u₁, and u₂. This shows the validity of the proposed duty cycle calculation method in this work.

When the reference voltage vector locates at other sectors, similar results can be obtained. Therefore, the validity of the presented strategy is verified in terms of theory, which provides a solid foundation for its popularization and application.

5. Experimental Results

To further verify the correctness of the presented algorithm, an experimental prototype illustrated in Figure 6 is designed, including a two-level voltage source inverter, a DC power source, an AC power source, and a filter. Here, DSP28335 is selected as the controller, where the software code of the proposed algorithm is running in it. The experimental waveforms and data are recorded using an eight-channel oscilloscope. The parameters of the experimental system used in this work are listed in

Table 3. System parameters.

Symbol	Parameters	Values
udc	DC voltage	250 V
e	Peak of back EMF	150 V
L	Filter inductance	20 mH
R	Parasitic resistance	0.05 Ω
T	Sampling period	66.67 μs

.

5.1. Steady State Results

To verify the validity of the presented dual-vector modulated MPC algorithm for two-level source inverters, its steady state control performance is tested and compared with the conventional single-vector MPC.

In the first experiment, the reference current is set as 3 and 8 A, with the frequency of the back EMF set as 50 Hz. The results are depicted in Figure 7, Figure 8, Figure 9 and Figure 10.

Figure 7 illustrates the current waveforms when the reference current is set as 3 A. It is obvious to see that the current ripples of the conventional MPC method are larger than that of the proposed dual-vector modulated MPC strategy in this paper, which shows the validity of the presented method in this work.

Furthermore, Figure 8 shows the current THDs of the traditional MPC method as well as the proposed MPC method when the current is 3 A. It can be known from Figure 8 that the current THD is decreased obviously when the proposed MPC method instead of the traditional MPC method is utilized to control the two-level voltage source inverter, which shows the superiority of the proposed method again.

Additionally, Figure 9 depicts the current waveforms of the two methods when the current is set as 8 A with the current THDs depicted in Figure 10.

It is clear to see from Figure 9 that the current ripples of the presented MPC strategy are decreased compared to the conventional MPC method. Meanwhile, the current THDs of the presented method in this article are also reduced, as illustrated in Figure 10, which verifies the validity of the presented dual-vector modulated MPC strategy as well as the theoretical analysis again.

Furthermore, to show the superiority of the presented algorithm with different currents, another experiment is carried out, and the current THDs are recorded, plotted, and finally illustrated in Figure 11.

Figure 11a shows the current THDs with different currents with the frequency set as 50 Hz. Figure 11b illustrates the current THDs with different currents at 20 Hz. It is apparent to see that the current THDs of the presented algorithm are decreased with different currents, which further verifies its validity.

5.2. Dynamic State Results

To further compare the dynamic state control performance of the presented algorithm with the conventional one, more experimental research is conducted here.

Figure 12a,b depicts the experimental waveforms of the double strategies when the current is stepped up from 3 to 8 A at 50 Hz. Figure 13a,b illustrates the results when the frequency is stepped up from 20 to 50 Hz with 8 A.

From Figure 12 and Figure 13, it can be concluded that both of the double strategies can achieve a satisfactory dynamic control effect, which shows the effectiveness of the presented method when the current is changed suddenly. Besides, it is clear to see from Figure 12 and Figure 13 that the current ripples of the presented dual-vector modulated MPC algorithm at steady state are lower than that of the conventional single-vector MPC method, which further verifies the effectiveness of the presented algorithm and the conducted theoretical analysis.

6. Extensions

Although the proposed dual-vector modulated MPC is aiming to control two-level voltage source inverters, further studies in this paper show that it can also be used to control other types of inverters by only changing the voltage vectors according to the corresponding inverter, which is another important contribution of this paper.

Here, a three-phase four-switch inverter is taken as an instance to show the correctness of the presented dual-vector modulated MPC.

Figure 14 shows the topology of the three-phase four-switch inverter. The four basic voltage vectors, i.e., V₁, V₂, V₃, and V₄, can be depicted as Figure 15, provided that the DC voltages are well balanced as many papers have studied the DC voltage balance control methods for three-phase four-switch inverters [33,34,35,36].

To reduce the current ripples, four hybrid voltage vectors are designed in the same way with (9), as shown in Figure 15, which are V_s1(V₁, V₂), V_s2(V₂, V₃), V_s3(V₃, V₄), and V_s4(V₄, V₁). In every control cycle, one of the four hybrid voltage vectors will be selected and utilized to reduce the current ripples.

The duty cycle of each voltage vector is calculated using the same method as (11). Then, after the four hybrid voltage vectors are determined, they are substituted into (8) to get an optimal one, which will then be utilized to control the three-phase four-switch inverter. The detailed implementation steps are similar to Figure 4. Furthermore, theoretical analysis and experimental studies are carried out to show its correctness and superiority.

6.1. Theoretical Analysis of the Proposed Method

For convenience, the voltage vector plane is divided into four sectors, as depicted in Figure 15. Here, the case that the reference voltage vector is located at sector I is taken as an example, as shown in Figure 16.

First, it is assumed that the end point of V_s1 is D, as shown in Figure 16.

Based on (9), (20) can be deduced.

$${\mathit{V}}_{\mathrm{s}1}={\mathit{V}}_1+d_{1,V2}({\mathit{V}}_2-{\mathit{V}}_1)$$

(20)

Thus, based on the geometrical relationship shown in Figure 16, (21) is deduced.

$$\{\begin{array}{l}\left|\mathrm{AD}\right|=d_{1,V2}\left|({\mathit{V}}_2-{\mathit{V}}_1)\right|\\ \left|\mathrm{BD}\right|=d_{1,V1}\left|({\mathit{V}}_2-{\mathit{V}}_1)\right|\end{array}$$

(21)

Meanwhile, according to the duty cycle calculation method in (11), it can be deduced that

$$\frac{d_{1,V1}}{d_{1,V2}}=\frac{\left|\mathrm{BD}\right|}{\left|\mathrm{AD}\right|}=\frac{\sqrt{G_2}}{\sqrt{G_1}}$$

(22)

According the defined cost function in (8), it can be known that

$$\{\begin{array}{l}{G}_1={\left|\mathrm{AC}\right|}^2\\ G_2={\left|\mathrm{BC}\right|}^2\end{array}$$

(23)

Thus, based on (22), it is calculated that

$$\frac{\left|\mathrm{BD}\right|}{\left|\mathrm{AD}\right|}=\frac{\left|\mathrm{BC}\right|}{\left|\mathrm{AC}\right|}$$

(24)

By rearranging (24) with the law of sines in consideration, (25) is obtained.

$$\frac{\sin \angle \mathrm{BCD}}{\sin \angle \mathrm{BDC}}=\frac{\left|\mathrm{BD}\right|}{\left|\mathrm{BC}\right|}=\frac{\left|\mathrm{AD}\right|}{\left|\mathrm{AC}\right|}=\frac{\sin \angle \mathrm{ACD}}{\sin \angle \mathrm{ADC}}$$

(25)

Considering that ∠BDC + ∠ADC = π, it can be known that

$$\sin \angle \mathrm{SDC}=\sin \angle \mathrm{ADC}$$

(26)

Thus, (27) is finally deduced based on (25) and (26).

$$\sin \angle \mathrm{BCD}=\sin \angle \mathrm{ACD}$$

(27)

Based on (27), it can be calculated that ∠BCD + ∠ACD = π or ∠BCD = ∠ACD. In the following, both of the two cases are analyzed respectively.

First, if ∠BCD + ∠ACD = π is true, it can be calculated that point C must be located on the segment AB. In this situation, it can be figured out based on (24) that point C and point D will be the same point. That means V_s1= u_αβref is true. Thus, the current control error can be minimized under this condition, which shows the validity of the duty cycle calculation method proposed in this article.

Second, if point C is not located on the segment AB, ∠BCD = ∠ACD should be true. In this situation, it can be obtained that ∠BCD = ∠ACD < ∠ADC as ∠ADC = ∠BCD +∠CBD. As ∠CAD < π/3 is true, and ∠CAD + ∠ADC + ∠ACD = π, it is obtained that ∠ADC + ∠ACD > 2π/3. As ∠ADC is larger than ∠ACD, ∠ADC > π/3 > ∠ACD can be obtained. As ∠CAD < π/3 and ∠ADC > π/3 are true, it can be known that ∠ADC > ∠CAD. Based on the law of sines, |AC| > |CD| is finally deduced. Since |AC| stands for the square root value of the cost function of V₁, and |CD| denotes that of V_s1, a conclusion is obtained, i.e., the control accuracy is increased when V_s1 is utilized to replace V₁.

Similarly, |BC| > |CD| can be proved, which means the control accuracy of V_s1 is increased compared to that of V₂. Thus, a conclusion is obtained, i.e., the proposed method is still effective when it is used to control the three-phase four-switch inverter. That is to say that the proposed method can be extended.

6.2. Experimental Verification

To validate the validity of the presented algorithm and the theoretical analysis shown above, experimental research is conducted, too. The parameters are the same as Table 3.

Figure 17 shows the current waveforms of the conventional single-vector MPC when the current is 4 A, while Figure 18 is the current waveforms of the proposed dual-vector modulated MPC under the same conditions.

It is clear to see from Figure 17 and Figure 18 that when the proposed dual-vector modulated MPC method is utilized instead of the conventional single-vector MPC method, the current THD is decreased by 51.3%, which verifies the correctness of the presented strategy and the theoretical analysis again.

Additionally, compared to the conventional deadbeat control theory-based dual-vector MPC method [13,14,15,16,17,18,19,20,21], the proposed method in this paper can reduce the computational time, mainly because the duty cycle calculation method of this paper is simpler with reduced mathematical operation than that of the conventional dual-vector MPC method [13,14,15,16,17,18,19,20,21]. Thus, less digital processing time is required. Furthermore, by using the proposed voltage-based cost function as well as the proposed voltage vector selection method in this paper, the computational time of the proposed method can be further reduced.

7. Conclusions

In this paper, a dual-vector modulated MPC is proposed based on the hypothesis that the duty cycle of each voltage vector is inversely proportional to the square root of its corresponding cost function value for two-level voltage source inverters. Theoretical analysis is conducted based on the geometrical relationship of the voltage vectors for the first time to prove the correctness of the presented method. Furthermore, comparative experimental results show the superiority of the presented modulated MPC strategy, too. Moreover, at the end of the paper, the proposed dual-vector modulated MPC is extended to control the three-phase four-switch inverter. Both the theoretical analysis and the experimental results verify its effectiveness. This is another important contribution of this paper.

In the future, the proposed method should be further studied to control many other kinds of inverters, including multilevel inverters and matrix inverters, as they have similar voltage vector planes, and research should also be done to analyze its effectiveness in a similar way.

Nevertheless, the proposed method also has a few disadvantages, one of which being that although it can reduce the current ripples and THDs compared to the single-vector MPC, it cannot minimize the current ripples and THDs at all operation regions. Although the theoretical analysis shows that the proposed method can reduce the control error at all operation regions and minimize it in several special operation regions, no evidence shows that it can minimize the control error at all operation regions. Therefore, to further solve the disadvantages of the proposed method shown above and improve its control performance, much work should be done in the future to minimize the control error of the proposed method at all operation regions.