Theoretical Comparison of Test Performance of Different Pulse Decay Methods for Unconventional Cores
Abstract
:1. Introduction
2. Testing Methods
- upstream positive-pulse (UPP);
- downstream negative-pulse (DNP);
- upstream positive- and downstream negative-pulse (UPDNP);
- upstream constant-pressure increase step (UCPIS);
- downstream constant-pressure reduction step (DCPRS);
- upstream positive-pulse and downstream constant-pressure (UPPDCP);
- upstream constant-pressure and downstream negative-pulse (UCPDNP);
- one-chamber (OC).
3. Test Performance on Homogeneous Media
3.1. Model of the Pulse Decay Test for Homogeneous Cores and Its Analytical Solution
3.1.1. Upstream Positive-Pulse Method
3.1.2. Downstream Negative-Pulse Method
3.1.3. Upstream Positive- and Downstream Negative-Pulse Method
3.1.4. Upstream Constant-Pressure Increase Step Method
3.1.5. Downstream Constant-Pressure Reduction Step Method
3.1.6. Upstream Positive-Pulse and Downstream Constant-Pressure Method
3.1.7. Upstream Constant-Pressure and Downstream Negative-Pulse Method
3.1.8. One-Chamber Method
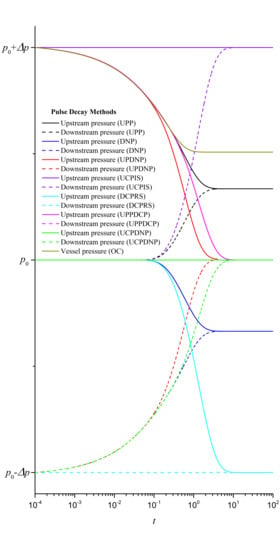
3.2. Pressure Equilibrium Time
3.3. Effect of the Porosity Error on the Permeability Precision
4. Identification of Dual Media
4.1. Characteristics of Pressure Curves
4.2. Characteristics of Pressure Derivative Curves
4.3. Effect on the Test Results of the Fracture Permeability
4.4. Pressure Equilibrium Time
5. Effect of Gas Adsorption
5.1. Effect on the Pressure Equilibrium Time
5.2. Effect on the Test Results of Permeability
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Brace, W.F.; Walsh, J.B.; Frangos, W.T. Permeability of granite under high pressure. J. Geophys. Res. 1968, 73, 2225–2236. [Google Scholar] [CrossRef]
- Hsieh, P.A.; Tracy, J.V.; Neuzil, C.E.; Bredehoeft, J.D.; Silliman, S.E. A transient laboratory method for determining the hydraulic properties of ‘tight’ rocks-I. Theory. Int. J. Rock Mech. Min. Sci. Geomechnics Abstr. 1981, 18, 245–252. [Google Scholar] [CrossRef]
- Jones, S.C. A technique for faster pulse-decay permeability measurements in tight rocks. SPE Form. Eval. 1997, 12, 19–25. [Google Scholar] [CrossRef]
- Civan, F.; Rai, C.S.; Sondergeld, C.H. Shale-gas permeability and diffusivity inferred by improved formulation of relevant retention and transprot mechanisms. Transp. Porous Media 2011, 86, 925–944. [Google Scholar] [CrossRef]
- Civan, F.; Rai, C.S.; Sondergeld, C.H. Determining shale permeability to gas by simultaneous analysis of various pressure tests. SPE J. 2012, 17, 717–726. [Google Scholar] [CrossRef]
- Feng, R.; Pandey, R. Invetigation of various pressure transient techniques on permeability measurement of unconventional gas reservoirs. Transp. Porous Media 2017, 120, 495–514. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.H. Pressure pulse-decay tests in a dual-continuum medium: An improved technique to estimate flow parameters. J. Nat. Gas Sci. Eng. 2019, 65, 16–24. [Google Scholar] [CrossRef]
- Alnoaimi, K.R.; Duchateau, C.; Kovscek, A.R. Characterization and measurement of multiscale gas transport in shale-core samples. SPE J. 2016, 21, 573–588. [Google Scholar] [CrossRef]
- Alnoaimi, K.R.; Kovscek, A.R. Influence of microcracks on flow and storage capacities of gas shales at core scale. Transp. Porous Media 2019, 127, 53–84. [Google Scholar] [CrossRef]
- Kamath, J.; Boyer, R.E.; Nakagawa, F.M. Characterization of core-scale heterogeneities using laboratory pressure transients. SPE Form. Eval. 1992, 7, 219–227. [Google Scholar] [CrossRef]
- Ning, X.; Fan, J.; Holditch, S.A.; Lee, W.J. The measurement of matrix and fracture properties in naturally fractured cores. In Proceedings of the Low Permeability Reservoirs Symposium, Denver, CO, USA, 26–28 April 1993. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.S.; Barati, R. Evaluation of core heterogeneity effect on pulse-decay experiment. In Proceedings of the International Symposium of the Society of Core Analysts, Vienna, Austria, 27 August–1 September 2017. [Google Scholar]
- Jia, B.; Tsau, J.; Barati, R. Experimental and numerical investigations of permeability in heterogeneous fractured tight porous media. J. Nat. Gas Sci. Eng. 2018, 58, 216–233. [Google Scholar] [CrossRef]
- Jia, B.; Tsau, J.; Barati, R.; Zhang, F. Impact of Heterogeneity on the transient gas flow process in tight rock. Energies 2019, 12, 3559. [Google Scholar] [CrossRef] [Green Version]
- Liu, H.; Lai, B.; Chen, J.; Georgi, D. Pressure pulse-decay tests in a dual-continuum medium: Late-time behavior. J. Petrol. Sci. Eng. 2016, 147, 292–301. [Google Scholar] [CrossRef]
- Cronin, M.B. Core-scale Heterogeneity and Dual-Permeability Pore Structure in the Barnett Shale. Ph.D. Thesis, The University of Texas, Austin, TX, USA, 2014. [Google Scholar]
- Han, G.; Sun, L.; Liu, Y.; Zhou, S. Analysis method of pulse decay tests for dual-porosity cores. J. Nat. Gas Sci. Eng. 2018, 59, 274–286. [Google Scholar] [CrossRef]
- Han, G.; Chen, Y.; Liu, M.; Liu, X. Differences in performance of models for heterogeneous cores during pulse decay tests. Appl. Sci. 2019, 9, 3206. [Google Scholar] [CrossRef] [Green Version]
- Aljamaan, H.; Al Ismail, M.; Kovscek, A.R. Experimental investigation and Grand Canonical Monte Carlo simulation of gas shale adsorption from the macro to the nano scale. J. Nat. Gas Sci. Eng. 2017, 48, 119–137. [Google Scholar] [CrossRef]
- Lin, K.; Huang, X.F.; Zhao, Y.P. Combining image recognition and simulation to reproduce the adsorption/desorption behaviors of shale gas. Energy Fuels 2020, 34, 258–269. [Google Scholar] [CrossRef]
- Zhou, S.; Ning, Y.; Wang, H.; Liu, H.; Xue, H. Investigation of methane adsorption mechanism on Longmaxi shale by combining the micropore filling and monolayer coverage theories. Adv. Geo-Energy Res. 2018, 2, 269–281. [Google Scholar] [CrossRef] [Green Version]
- Cui, X.; Bustion, A.M.M.; Bustion, R.M. Measurements of gas permeability and diffusivity of tight reservoir rocks: Different approaches and their applications. Geofluids 2009, 9, 208–223. [Google Scholar] [CrossRef]
- Han, G.; Chen, Y.; Liu, X. Investigation of analysis methods for pulse decay tests considering gas adsorption. Energies 2019, 12, 2562. [Google Scholar] [CrossRef] [Green Version]
- Akkutlu, I.Y.; Fathi, E. Multiscale gas transport in shales with local kergen heterogeneities. SPE J. 2012, 1002–1011. [Google Scholar] [CrossRef] [Green Version]
- Zoback, M.D.; Byerlee, J.D. Permeability and effective stress. AAPG Bull. 1975, 59, 154–158. [Google Scholar] [CrossRef]
- Metwally, Y.M.; Sondergeld, C.H. Measuring low permeabilities of gas-sands and shales using a pressure transmission technique. Int. J. Rock Mech. Min. 2011, 48, 1135–1144. [Google Scholar] [CrossRef]
- Tinni, A.; Fathi, E.; Agarwal, R.; Sondergeld, C.; Akkutlu, Y.; Rai, C. Shale permebaility measurements on plugs and crushed samples. In Proceedings of the SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar] [CrossRef]
- Heller, R.; Vermylen, J.; Zoback, M. Experimental investigation of matrix permeability of gas shales. AAPG Bull. 2014, 98, 975–995. [Google Scholar] [CrossRef]
- Yang, Z.; Sang, Q.; Dong, M.; Zhang, S.; Li, Y.; Gong, H. A modified pressure-pulse decay method for determining permeabilities of tight reservoir cores. J. Nat. Gas Sci. Eng. 2015, 27, 236–246. [Google Scholar] [CrossRef]
- Feng, R.; Liu, J.; Harpalani, S. Optimized pressure pulse-decay method for laboratory estimation of gas permeability of sorptive reservoirs: Part 1-background and numerical analysis. Fuel 2017, 191, 555–564. [Google Scholar] [CrossRef]
- Dicker, A.I.; Smits, R.M. A practical approach for determining permeability from laboratory pressure-pulse decay measurements. In Proceedings of the 1988 SPE International Meeting on Petroleum Engineering, Tianjin, China, 1–4 November 1988. [Google Scholar] [CrossRef]


















| Method | Error (%) | |||||
|---|---|---|---|---|---|---|
| Storativity Ratio | Interporosity Flow Coefficient | |||||
| 0.01 | 0.1 | 0.2 | 10−3 | 10−4 | 10−5 | |
| UPP | 16.2 | 14.5 | 12.7 | 14.4 | 14.5 | 14.5 |
| DNP | 16.2 | 14.5 | 12.7 | 14.3 | 14.5 | 14.5 |
| UPDNP | 16.2 | 14.5 | 12.7 | 14.4 | 14.5 | 14.5 |
| UCPIS | 33.5 | 29.8 | 25.8 | 28.6 | 29.8 | 30.0 |
| DCPRS | 33.6 | 29.8 | 25.7 | 28.5 | 29.8 | 30.0 |
| UPPDCP | 33.9 | 30.1 | 26.1 | 30.2 | 30.1 | 30.0 |
| UCPDN | 33.9 | 30.1 | 26.1 | 30.2 | 30.1 | 30.0 |
| OC | 5933.5 | 541.9 | 245.7 | 538.7 | 541.9 | 543.7 |
| Group | First | Second | Third | Fourth |
|---|---|---|---|---|
| Method | UPP, DNP, OC | UCPIS, DCPRS | UPPDCP, UCPDNP | UPDNP |
| Final equilibrium time | Longest | Second longest | Further reduced | Shortest |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, G.; Liu, X.; Huang, J. Theoretical Comparison of Test Performance of Different Pulse Decay Methods for Unconventional Cores. Energies 2020, 13, 4557. https://doi.org/10.3390/en13174557
Han G, Liu X, Huang J. Theoretical Comparison of Test Performance of Different Pulse Decay Methods for Unconventional Cores. Energies. 2020; 13(17):4557. https://doi.org/10.3390/en13174557
Chicago/Turabian StyleHan, Guofeng, Xiaoli Liu, and Jin Huang. 2020. "Theoretical Comparison of Test Performance of Different Pulse Decay Methods for Unconventional Cores" Energies 13, no. 17: 4557. https://doi.org/10.3390/en13174557
APA StyleHan, G., Liu, X., & Huang, J. (2020). Theoretical Comparison of Test Performance of Different Pulse Decay Methods for Unconventional Cores. Energies, 13(17), 4557. https://doi.org/10.3390/en13174557