1. Introduction
Planning the operation of a power generation system is defined by establishing the use of energy sources in the most efficient way [
1,
2,
3]. Renewable sources are those with the lowest operation cost since the fuel is provided free of charge by nature. Good predictions of river streamflows allow resource management according to their future availability [
4]. Therefore, this is mandatory for countries where there are hydroelectric plants [
5,
6,
7].
The International Hydropower Association published the Hydropower Status Report 2020 [
8], showing that 4306 TWh of electricity was generated in the world using hydroelectric plants in 2019. This amount represents the single most significant contribution from a renewable energy source in history. The document summarizes data from 13,000 stations in 150 countries. The top countries in hydropower installed capacity are China (356.40 GW), Brazil (109.06 GW), United States (102.75 GW), and Canada (81.39 GW).
In this context, it is important to predict accurate information about rivers’ monthly seasonal streamflow, since it makes the turbines spin, transforming kinetic into electric energy [
5,
9]. These series present a specific seasonal behavior due to the volume of water throughout the year being mostly dependent on rainfall [
10,
11]. Ensuring efficient operation of such plants is needed, since it significantly impacts cost of production and suitable use of water [
12,
13]. Additionally, their operation leads to a smaller environmental impact than burning carboniferous fuel. Due to this, many pieces of research have presented investigations on such fields for countries such as China [
14], Canada [
15], Serbia [
16], Norway [
17], Malaysia [
7], and Brazil [
9].
Linear and nonlinear methodologies have been proposed to solve this problem. As discussed in [
5,
12], and [
18], the linear methods of the Box-Jenkins family are widely used [
19]. The autoregressive model (AR) is highlighted because its easy implementation process allows the calculation of its free coefficients in a simple and deterministic manner. An extended proposal for this task is the autoregressive and moving average model (ARMA), a more general methodology that uses the errors of past predictions to form the output response [
19,
20].
However, artificial neural networks (ANN) are prominent for this kind of problem [
9,
21,
22,
23,
24]. They were inspired by the operation of the nervous system of superior organisms, recognizing data regularities and patterns through training and determining generalizations based on the acquired knowledge [
18,
25,
26,
27].
In recent times, some studies have indicated that the best results for time series forecasting can be achieved by combining different predictors using ensembles [
28,
29,
30]. Many authors have applied these techniques to similar tasks [
31,
32,
33]. However, the approaches commonly explore only the average of the single models output or the classic neural networks (multilayer perceptron (MLP) and radial basis function networks (RBF)) as a combiner. The specialized literature regarding streamflow forecasting shows that ANN approaches stand out, but some authors use linear models [
16], support vector regression [
14], and ensembles [
15].
This work proposes using a special class of neural networks, the unorganized machines (UM), to solve the aforementioned forecasting task. The term UM defines the extreme learning machines (ELM) and echo state network (ESN) collectively. In this investigation, we addressed six versions of UMs: ELM with and without regularization coefficient (RC) as well as ESN using the reservoir designs from Jaeger’s and Ozturk et al. with and without RC. Additionally, we addressed the ELM and the ELM (RC) as the combiner of a neural-based ensemble.
To realize an extensive comparative study, we addressed two linear models (AR and ARMA models); four well-known artificial neural networks (MLP, RBF, Elman network, Jordan Network); and four other ensembles, using as combiners the average, the median, the MLP, and the RBF. To the best of our knowledge, the use of ELM ensembles in this problem and similar repertoires of models is an investigation not yet accomplished. Therefore, we would like to fill this gap.
In this study, the database is from Brazil. In the country, electric energy is mostly generated by hydroelectric plants, these being responsible for 60% of all electric power produced in 2018 [
8,
34,
35]. In addition, Brazil is the one of the largest producers of hydropower in the world. Therefore, the results achieved can be extensible for other countries.
The remainder of this work is organized as follows:
Section 2 discusses the linear models from the Box-Jenkins methodology;
Section 3 presents the artificial neural networks and the ensembles;
Section 4 shows the case study, the details on the seasonal streamflow series, the computational results, and the result analysis; and
Section 5 shows the conclusions.
4. Case Study
Streamflow series are a kind of time series in which each observation refers to monthly, weekly, daily, or hourly average flow. This work addresses the monthly average flow. These series present seasonality since they follow the rain cycles that occur during the year [
9]. Seasonality changes the standard behavior of the series, which must be adjusted to improve the response of predictors [
5].
Deseasonalization is an operation that removes the seasonal component of the monthly series. They become stationary, presenting zero mean and unitary standard deviation. The new deseasonalized series is given by Equation (16) [
50]:
in which
is the new standardized value of the
element of the series,
is the value of the element
in the original series,
is the average of all elements of the series in the month
, and
is the standard deviation of all elements of the series in the month
.
This investigation addressed the series of the following Brazilian hydroelectric plants: Agua Vermelha, Belo Monte, Ilha Solteira, Paulo Afonso, and Tucuru. All data were obtained from the National Electric System Operator (ONS) and are available on its website [
65]. These plants were selected because of their location in different regions of the country, and, as shown in
Table 1, they have different hydrological behavior. Therefore, it is possible to accomplish a robust performance analysis.
All series comprise samples from January of 1931 to December of 2015, a total of 85 years, or 1020 months. The data were divided into three sets: from 1931 to 1995 is the training set, used to adjust the free parameters of the models; from 1996 to 2005 is the validation set, used in the cross-validation process and to adjust the value of the regularization coefficient of ELMs and ESNs; and from 2006 to 2015 is the test set, utilized to measure the performance of the models. The mean squared error (MSE) was adopted as the performance metric, as done in other works of the area [
12].
Predictions were made using up to the last six delays of the samples as inputs. These delays were selected using the wrapper method [
66,
67]. The predictions were performed for 1 (next month), 3 (next season), 6 (next semester), and 12 (next year) steps ahead, using the recursive prediction technique [
68,
69].
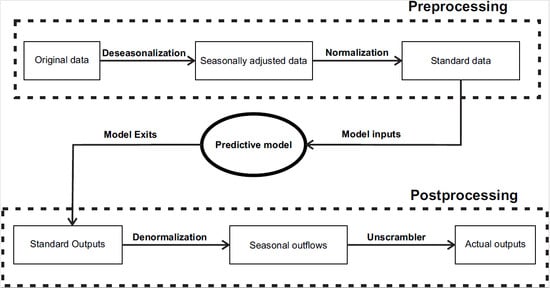
During the preprocessing stage, the series’ seasonal component was removed through deseasonalization to make the behavior almost stationary. Therefore, the predicted values required an additional postprocessing step, where the data had the seasonal component reinserted.
Figure 5 shows step by step the entire prediction process.
In total, this work applied 18 predictive methods, two of which were linear methods of the Box-Jenkins family, 10 artificial neural networks, and six ensembles:
AR()—autoregressive model of order , optimized by the Yule–Walker equations;
ARMA()—autoregressive–moving-average model of order , optimized by maximum likelihood estimators;
MLP—MLP network with a hidden layer;
RBF—RBF network;
ELM—ELM network;
ELM (RC)—ELM with the regularization coefficient;
Elman—Elman network;
Jordan—Jordan network;
Jaeger ESN—ESN with reservoir from Jaeger;
Jaeger ESN (RC)—ESN from Jaeger and regularization coefficient;
Ozturk ESN—ESN with reservoir from Ozturk et al.;
Ozturk ESN (RC)—ESN with reservoir from Ozturk et al. and regularization coefficient;
Average Ensemble—ensemble with mean as arithmetic combiner;
Median Ensemble—ensemble with median as arithmetic combiner;
MLP Ensemble—ensemble with MLP as combiner;
RBF Ensemble—ensemble with an RBF as combiner;
ELM Ensemble—ensemble with ELM as combiner;
ELM Ensemble (RC)—ensemble with an ELM with regularization coefficient as combiner.
All neural networks used the hyperbolic tangent as activation function with . The learning rate adopted for the models, which use backpropagation, was . As a stopping criterion, a minimum improvement in MSE of or a maximum of 2000 epochs was considered. The networks were tested for the number of neurons from 5 to 200, with an increase of 5 neurons. All these parameter’s values were determined after empirical tests.
The regularization coefficients were evaluated with all the 52 possibilities mentioned in
Section 3.4. The one with the lowest MSE in the validation set was chosen for ELM and ESN approaches. The wrapper method was used to select the best lags to the single models as well as which experts were the best predictors when using the ensembles. The holdout cross-validation was also applied to all fully neural networks and ensembles to avoid overtraining and to determine the
of ELM and ESN.
All proposed models were executed 30 times to obtain sample output data for each input configuration and number of neurons, these having been chosen as the best executions. Additionally, following the methodology addressed in [
9] and [
70], we adjusted 12 independent models, one for each month, for all proposed methods. It is allowed since the mean and the variance of each month are distinct, and this approach can lead to better results [
9].
Experimental Results
In this section, we present and discuss the results obtained by all models and four forecasting horizons.
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 show the results achieved for Agua Vermelha, Belo Monte, Ilha Solteira, Paulo Afonso, and Tucurui hydroelectric plants, for both real and deseasonalized domains. The best performances are highlighted in bold.
The Friedman [
71,
72] test was applied to the results for the 30 runs of each predictive model proposed, regarding the MSE in the test set. The
p-values achieved were smaller than 0.05. Therefore, we can assume that changing the predictor leads to a significant change in the results.
To analyze the dispersion of the results obtained after 30 executions [
73],
Figure 6 presents the boxplot graphic [
72,
74].
Note that AR, ARMA, average ensemble, and median ensemble models did not show dispersion since they presented close-form solution [
75]. One can verify the highest dispersion was obtained by RBF, while the lowest was achieved by Elman network.
Many aspects of the general results presented in
Table 2,
Table 3,
Table 4,
Table 5 and
Table 6 can be discussed. The first is that the best predictor in the real space sometimes was not the same in the deseasonalized domain. This occurred because the deseasonalization process considered all parts of the series as having the same importance. In the literature, the error in the real space is adopted as the most important measure to evaluate the results [
12,
18].
As the forecasting horizon grows, the prediction process becomes more difficult, and the errors tend to increase for all models. It is directly related to the decreased correlation between the input samples and the desired future response. Therefore, the output estimates tend to achieve the long term mean, or the historical mean [
9].
For
step ahead, for all series, the best predictor was always an ensemble, highlighting the ELM-based combiner, which was the best for three of five scenarios (60%). This result indicates that the use of ensembles can lead to an increase in the performance. Moreover, the application of an unorganized machine requires less computational effort than the MLP or the RBF since its training process is based on a deterministic linear approach. It also corroborates that their approximation capability is elevated, overcoming their fully trained counterpart [
9,
12].
The results varied for , for which several architectures—ELM, Jaeger ESN, average ensemble, and MLP ensemble—were the best at least once. We emphasize that the ELM network was better in two cases, and the ESN in one. The UMs were better in 60% of the cases. Regarding , the ELM was also the best predictor, achieving the smallest error in four cases (80%), followed by the MLP, which was the best only for Tucurui.
Analyzing the last forecasting horizon, , four different neural architectures reached the best performance at least once: MLP, Elman, Jaeger ESN (twice), and Ozturk ESN (RC). An important observation is the presence of recurrent models among them. This horizon is very difficult to predict since the correlation between the input samples and the desired response is small. Therefore, there is an indication that the existence of model’s internal memory is an advantage.
In summary, the unorganized networks (ESN and ELM), in stand-alone versions or as a combiner of an ensemble, provided the best results in 14 of 20 scenarios (70%). This is relevant since such methods are newer than the others and are simpler to implement.
Considering the reservoir design of ESNs, we achieved almost a draw; in nine cases, the proposal from Ozturk et al. was the best, and in 11, the Jaeger model achieved the smallest error. Therefore, we cannot state which one is the most adequate for the problem.
Regarding the feedforward neural models, one can observe for 16 of 20 cases (80%), the ELMs overcame the traditional MLP and RBF architectures. In the same way, the ESNs were superior to the traditional and the fully trained Elman and Jordan proposals in 17 of 20 scenarios (85%). This is strong evidence that the unorganized models are prominent candidates to carry out such problems.
Linear models did not outperform neural networks in any of the 20 scenarios. For the problem of forecasting monthly seasonal streamflow series, the results showed that ANNs were most appropriate. However, it is worth mentioning that linear models are still widely used in current days.
Finally, to provide a visual appreciation of the final simulation,
Figure 7 presents the forecast made by the ELM ensemble for Água Vermelha plant with
.
5. Conclusions
This work investigated the performance of unorganized machines—extreme learning machines (ELM), echo state networks (ESN), and ELM-based ensembles—on monthly seasonal streamflow series forecasting from hydroelectric plants. This is a very important task for countries where power generation is highly dependent on water as a source, such as Canada, China, Brazil, and the USA, among others. Due to the broad use of this kind of energy generation in the world, even a small improvement in the accuracy of the predictions can lead to significant financial resource savings as well as a reduction in the impact of using fossil fuels.
We also used many artificial neural network (ANN) architectures—multilayer perceptron (MLP), radial basis function networks (RBF), Jordan network, Elman network, and the ensemble methodology using the mean, the median, the MLP, and the RBF as combiner. Moreover, we compared the results with the traditional AR and ARMA linear models. We addressed four forecast horizons, , , , and steps ahead, and the wrapper method to select the best delays (inputs).
The case study involves a database related to five hydroelectric plants. The tests showed that the neural ensembles were the most indicated for = 1 since they presented the best performances in all the simulations of this scenario, especially those that employed the ELM. For = 3 and 6, the ELM was highlighted. For = 12, it was clear that the recurrent models were outstanding, mainly those with the ESN.
Regarding the linear models, this work showed its inferiority in comparison to the neural ones in all cases. Furthermore, the unorganized neural models (ELM and ESN), in their stand-alone versions or as combiners of the ensemble, prevailed over the others, presenting 14 of the lowest errors (70%).
These results are important since the unorganized machines are easy to implement and require less computational effort than the fully trained approaches. This is related to the use of the Moore-Penrose inverse operator to train their output layer, since it ensures the optimum value of the weights in the mean square error sense. The use of the backpropagation could lead the process to a local minimum, indicating how difficult the problem is. In at least 80% of the cases, the unorganized proposals (ELM and ESN) overcame the fully trained proposals (MLP, RBF, Elman, and Jordan).
Other deseasonalization processes should be investigated in future works. Additionally, the streamflow from distinct plants must be predicted and the results evaluated. Moreover, the use of bio-inspired optimization methods [
76,
77,
78] is encouraged to optimize the ARMA model and the application of the support vector regression method.