Thin Solid Film Electrolyte and Its Impact on Electrode Polarization in Solid Oxide Fuel Cells Studied by Three-Dimensional Microstructure-Scale Numerical Simulation
Abstract
:1. Introduction
2. Mathematical and Numerical Model
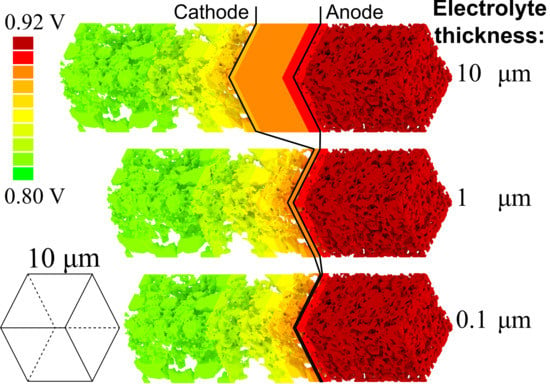
3. Results
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| Abbreviations | ||
| DPB | Double Phase Boundary | |
| FIB | Focused Ion Beam | |
| GDC | Gadolinum Doped Ceria | |
| LSCF | Lanthanum Strontium Cobalt Ferrite | |
| OCV | Open Circuit Voltage | |
| PEN | Positive Electrolyte Negative | |
| SEM | Scanning Electron Microscopy | |
| SOFC | Solid Oxide Fuel Cell | |
| SOR | Successive Over-Relaxation | |
| TPB | Triple Phase Boundary | |
| YSZ | Yttrium-Stabilized Zirconia | |
| Roman symbols | ||
| F | Faraday constant | |
| i | Charge transfer rate | |
| Equilibrium exchange current density at TPB | ||
| Equilibrium exchange current density at DPB | ||
| j | Mean charge transfer rate | |
| TPB density | ||
| DPB density | ||
| R | Universal gas constant | |
| T | Temperature | K |
| x, y | Planar coordinates | m |
| z | Depth (distance from anodic channel) | m |
| Greek symbols | ||
| Charge transfer coefficient | - | |
| Overpotential | V | |
| Electrical potential | V | |
| Electrical conductivity | ||
| Tortuosity | - | |
| Phase volume fraction | - | |
| Subscripts | ||
| act | Activation | |
| b | Boundary (bulk) | |
| dpb | Double Phase Boundary | |
| Hydrogen | ||
| Water vapor | ||
| Oxygen | ||
| i | A substance | |
| ion | Oxide ion conducting phase | |
| tpb | Triple phase boundary | |
| dpb | Double phase boundary | |
| 0 | Equilibrium | |
| Superscripts | ||
| ano | anodic | |
| cath | cathodic | |
References
- Pianko-Oprych, P.; Hosseini, S.M. Dynamic Analysis of Load Operations of Two-Stage SOFC Stacks Power Generation System. Energies 2017, 10, 2103. [Google Scholar] [CrossRef] [Green Version]
- Fang, X.; Zhu, J.; Lin, Z. Effects of Electrode Composition and Thickness on the Mechanical Performance of a Solid Oxide Fuel Cell. Energies 2018, 11, 1735. [Google Scholar] [CrossRef] [Green Version]
- Gandiglio, M.; De Sario, F.; Lanzini, A.; Bobba, S.; Santarelli, M.; Blengini, G.A. Life Cycle Assessment of a Biogas-Fed Solid Oxide Fuel Cell (SOFC) Integrated in a Wastewater Treatment Plant. Energies 2019, 12, 1611. [Google Scholar] [CrossRef] [Green Version]
- Coddet, P.; Liao, H.L.; Coddet, C. A review on high power SOFC electrolyte layer manufacturing using thermal spray and physical vapour deposition technologies. Adv. Manuf. 2014. [Google Scholar] [CrossRef]
- Noh, H.S.; Lee, H.; Kim, B.K.; Lee, H.W.; Lee, J.H.; Son, J.W. Microstructural factors of electrodes affecting the performance of anode-supported thin film yttria-stabilized zirconia electrolyte (1 μm) solid oxide fuel cells. J. Power Sources 2011. [Google Scholar] [CrossRef]
- Baek, J.D.; Liu, K.Y.; Su, P.C. A functional micro-solid oxide fuel cell with a 10 nm-thick freestanding electrolyte. J. Mater. Chem. A 2017, 5, 18414–18419. [Google Scholar] [CrossRef]
- Wilson, J.R.; Kobsiriphat, W.; Mendoza, R.; Chen, H.Y.; Hiller, J.M.; Miller, D.J.; Thornton, K.; Voorhees, P.W.; Adler, S.B.; Barnett, S.A. Three-dimensional reconstruction of a solid-oxide fuel-cell anode. Nat. Mater. 2006, 5, 541–544. [Google Scholar] [CrossRef]
- Suzue, Y.; Shikazono, N.; Kasagi, N. Micro modeling of solid oxide fuel cell anode based on stochastic reconstruction. J. Power Sources 2008, 184, 52–59. [Google Scholar] [CrossRef]
- Shikazono, N.; Kanno, D.; Matsuzaki, K.; Teshima, H.; Sumino, S.; Kasagi, N. Numerical Assessment of SOFC Anode Polarization Based on Three-Dimensional Model Microstructure Reconstructed from FIB-SEM Images. J. Electrochem. Soc. 2010, 157, B665–B672. [Google Scholar] [CrossRef] [Green Version]
- Kanno, D.; Shikazono, N.; Takagi, N.; Matsuzaki, K.; Kasagi, N. Evaluation of SOFC anode polarization simulation using three-dimensional microstructures reconstructed by FIB tomography. Electrochim. Acta 2011, 56, 4015–4021. [Google Scholar] [CrossRef]
- Kishimoto, M.; Iwai, H.; Saito, M.; Yoshida, H. Three-Dimensional Simulation of SOFC Anode Polarization Characteristics Based on Sub-Grid Scale Modeling of Microstructure. J. Electrochem. Soc. 2012, 159, B315–B323. [Google Scholar] [CrossRef] [Green Version]
- Carraro, T.; Joos, J.; Rüger, B.; Weber, A.; Ivers-Tiffée, E. 3D finite element model for reconstructed mixed-conducting cathodes: I. Performance quantification. Electrochim. Acta 2012, 77, 315–323. [Google Scholar] [CrossRef]
- Baek, J.D.; Yoon, Y.J.; Lee, W.; Su, P.C. A circular membrane for nano thin film micro solid oxide fuel cells with enhanced mechanical stability. Energy Environ. Sci. 2015. [Google Scholar] [CrossRef]
- Chen, Z.; Wang, X.; Brandon, N.; Atkinson, A. Numerical Study of Solid Oxide Fuel Cell Contacting Mechanics. Fuel Cells 2018, 18, 42–50. [Google Scholar] [CrossRef]
- Park, J.; Kim, D.; Baek, J.; Yoon, Y.J.; Su, P.C.; Lee, S. Effect of Electrolyte Thickness on Electrochemical Reactions and Thermo-Fluidic Characteristics inside a SOFC Unit Cell. Energies 2018, 11, 473. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Zhang, Y.; Baker, J.; Majumdar, P.; Yang, Z.; Han, M.; Chen, F. Hierarchically oriented macroporous anode-supported solid oxide fuel cell with thin ceria electrolyte film. ACS Appl. Mater. Interfaces 2014, 6, 5130–5136. [Google Scholar] [CrossRef] [PubMed]
- Iwai, H.; Kadomiya, R.; Kishimoto, M.; Saito, M.; Yoshida, H. Numerical analysis of cross-electrode interaction in SOFCs with thin electrolyte. In Proceedings of the 13th European SOFC & SOE Forum 2018, Luzern, Switzerland, 3–6 July 2018. [Google Scholar]
- Kishimoto, M.; Sasaki, M.; Iwai, H.; Yoshida, H. Numerical assessment of mesoscale modification of thin electrolyte in anode-supported solid oxide fuel cells. In Proceedings of the 13th European SOFC & SOE Forum 2018, Luzern, Switzerland, 3–6 July 2018; p. A1305. [Google Scholar]
- Prokop, T.; Berent, K.; Iwai, H.; Szmyd, J.S.; Brus, G. A three-dimensional heterogeneity analysis of electrochemical energy conversion in SOFC anodes using electron nanotomography and mathematical modeling. Int. J. Hydrogen Energy 2018, 43, 10016–10030. [Google Scholar] [CrossRef]
- Prokop, T.; Berent, K.; Szmyd, J.S.; Brus, G. A three-dimensional numerical assessment of heterogeneity impact on a solid oxide fuel cell’s anode performance. Catalyst 2018, 8, 503. [Google Scholar] [CrossRef] [Green Version]
- Prokop, T.A.; Berent, K.; Mozdzierz, M.; Szmyd, J.S.; Brus, G. A Three-Dimensional Microstructure-Scale Simulation of a Solid Oxide Fuel Cell Anode—The Analysis of Stack Performance Enhancement After a Long-Term Operation. Energies 2019, 12, 4784. [Google Scholar] [CrossRef] [Green Version]
- Matsuzaki, K.; Shikazono, N.; Kasagi, N. Three-dimensional numerical analysis of mixed ionic and electronic conducting cathode reconstructed by focused ion beam scanning electron microscope. J. Power Sources 2011, 196, 3073–3082. [Google Scholar] [CrossRef]
- Miyoshi, K.; Miyamae, T.; Iwai, H.; Saito, M.; Kishimoto, M.; Yoshida, H. Exchange current model for (La0.8Sr0.2)0.95MnO3 (LSM) porous cathode for solid oxide fuel cells. J. Power Sources 2016, 315, 63–69. [Google Scholar] [CrossRef] [Green Version]
- Kim, Y.T.; Jiao, Z.; Shikazono, N. Evaluation of La0.6Sr0.4Co0.2Fe0.8O3-δ-Gd0.1Ce0.9O1.95 composite cathode with three dimensional microstructure reconstruction. J. Power Sources 2017, 342, 787–795. [Google Scholar] [CrossRef]
- de Boer, B. Hydrogen Oxidation at Porous Nickel and Nickel/Yttria Stabilised Zirconia Cermet Electrodes. Ph.D. Thesis, Universiteit Twente, Enschede, The Netherlands, 1998. [Google Scholar]
- Holtappels, P.; de Haart, L.G.J.; Stimming, U. Reaction of Hydrogen/Water Mixtures on Nickel-Zirconia Cermet Electrodes: I. DC Polarization Characteristics. J. Electrochem. Soc. 1999, 146, 1620–1625. [Google Scholar] [CrossRef]
- Brus, G.; Iwai, H.; Szmyd, J.S. An Anisotropic Microstructure Evolution in a Solid Oxide Fuel Cell Anode. Nanoscale Res. Lett. 2020, 15, 3. [Google Scholar] [CrossRef] [PubMed]
- Mozdzierz, M.; Berent, K.; Kimijima, S.; Szmyd, J.S.; Brus, G. A Multiscale Approach to the Numerical Simulation of the Solid Oxide Fuel Cell. Catalysts 2019, 9, 253. [Google Scholar] [CrossRef] [Green Version]
- Hunter, J.D. Matplotlib: A 2D graphics environment. Comput. Sci. Eng. 2007, 9, 90–95. [Google Scholar] [CrossRef]










| Phase | |||||||
|---|---|---|---|---|---|---|---|
| Cathode | |||||||
| LSCF | GDC | Pore | |||||
| × 1012 | × 106 | 0.34 | 3.95 | 0.27 | 10.32 | 0.39 | 2.42 |
| Anode | |||||||
| Ni | YSZ | Pore | |||||
| × 1012 | 0.349 | 4.95 | 0.462 | 3.009 | 0.159 | 26.159 | |

© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Prokop, T.A.; Brus, G.; Kimijima, S.; Szmyd, J.S. Thin Solid Film Electrolyte and Its Impact on Electrode Polarization in Solid Oxide Fuel Cells Studied by Three-Dimensional Microstructure-Scale Numerical Simulation. Energies 2020, 13, 5127. https://doi.org/10.3390/en13195127
Prokop TA, Brus G, Kimijima S, Szmyd JS. Thin Solid Film Electrolyte and Its Impact on Electrode Polarization in Solid Oxide Fuel Cells Studied by Three-Dimensional Microstructure-Scale Numerical Simulation. Energies. 2020; 13(19):5127. https://doi.org/10.3390/en13195127
Chicago/Turabian StyleProkop, Tomasz A., Grzegorz Brus, Shinji Kimijima, and Janusz S. Szmyd. 2020. "Thin Solid Film Electrolyte and Its Impact on Electrode Polarization in Solid Oxide Fuel Cells Studied by Three-Dimensional Microstructure-Scale Numerical Simulation" Energies 13, no. 19: 5127. https://doi.org/10.3390/en13195127
APA StyleProkop, T. A., Brus, G., Kimijima, S., & Szmyd, J. S. (2020). Thin Solid Film Electrolyte and Its Impact on Electrode Polarization in Solid Oxide Fuel Cells Studied by Three-Dimensional Microstructure-Scale Numerical Simulation. Energies, 13(19), 5127. https://doi.org/10.3390/en13195127