Pressure-Transient Performances of Fractured Horizontal Wells in the Compartmentalized Heterogeneous Unconventional Reservoirs
Abstract
:1. Introduction
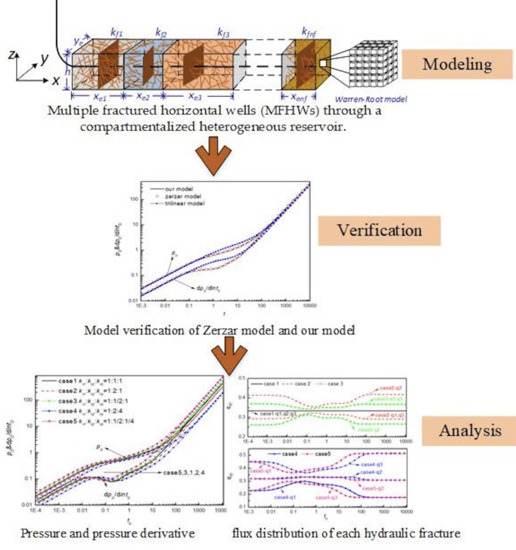
2. Modeling of MFHWs
2.1. Physical Model and Assumptions
- (1)
- The reservoir is heterogeneous along the horizontal wellbore with nf blocks of different length xei (i = 1, 2, 3, …, nf), and there is one hydraulic fracture distributed in each block. The thickness of the stimulated reservoir volume is uniform h and width is ye. The initial pressure is assumed pi.
- (2)
- The artificial hydraulic fractures are vertical to the horizontal wellbore, with fracture half-length Lfi, fracture height hfi, (i = 1, 2, 3, …, nf), and uniform flux distribution assumed in each hydraulic fracture.
- (3)
- Each block of unconventional reservoir was established by Warren and Root’s (1963) dual porosity model, where natural fractures and matrix follow the Darcy’s flow model. For each blocks, different natural fracture permeability kfi, crossflow coefficient λi, and elastic storage ratio ωi (i = 1, 2, 3, …, nf) can be defined.
- (4)
- The fluid assumed slightly compressible with constant viscosity and compressibility.
- (5)
- Gravity and capillary effect are negligible.
2.2. Pressure Solution for a Reservoir Substructure
2.3. Source Functions for the Inner and Outer Boundaries
3. Solution of Coupling Multiple Blocks
- (1)
- Continuity conditions of pressure and flux at the interface
- (2)
- Horizontal wellbore conditions
4. Comparison and Verification
5. Results and Discussion
5.1. Heterogeneous Permeability
5.2. Non-Uniform Length of Blocks
5.3. Different Elastic Storage Ratio
5.4. Different Crossflow Ratio
5.5. Non-Uniform Half-Length Distribution of Fractures
6. Conclusions
- (1)
- This model only discretizes hydraulic fractures and interface boundaries. With a small number of segments interface discretization, it can match verified model very well on the log–log plots. As a result, this model can greatly reduce fine gridding required by numerical approach.
- (2)
- Compared to the trilinear flow model, this model can consider the radial flow around the hydraulic fracture, and the interference effect between hydraulic fractures with different formation properties.
- (3)
- As the permeability increases along the horizontal well direction, the pressure drop decreases and flow regimes become earlier. The fractures flux fluctuates with flow regimes, where the difference between high- and low-permeability blocks decreases firstly, then increases gradually, and tends to be stable finally. When the entire drainage length keeps constant, the pressure responses have nothing to do with non-uniform heterogeneous block length while flux distribution has been changed obviously.
- (4)
- The elastic storage ratio mainly affects the early flow regimes including first linear flow, first radial flow and crossflow periods. The bigger the elastic storage ratio, the smaller the groove and the greater the flux. However, the crossflow ratio only affects the crossflow period. The bigger the crossflow ratio, the earlier the crossflow arrives.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| A | coefficient matrix |
| B | right-hand side vector |
| BWD | The dimensionless inner surface domain |
| BeD | The dimensionless outer surface domain |
| Ct | the total compressibility, MPa−1 |
| G | Green’s function |
| h | the reservoir thickness, m |
| k | permeability, mD |
| kfi | the ith fracture permeability, mD |
| Lfi | the ith fracture half-length, m |
| l | The characteristic reference length, m |
| MD | The observation locations in dimensionless space |
| The source locations in dimensionless space | |
| me | interface segment number |
| nf | the hydraulic fractures number |
| pi | initial reservoir pressure, MPa |
| Δp | Pressure drop, MPa |
| pD | the dimensionless pressure value |
| qtotal | the total wellbore flow rate, m3/d |
| tD | the dimensionless time |
| X | The solution vector |
| xe | the length of blocks |
| ye | the width of reservoir |
| λi | The ith block crossflow coefficient |
| ωi | The ith block elastic storage ratio |
| μ | Viscosity |
| ϕ | Porosity |
Subscripts and Superscripts
| D | dimensionless |
| e | boundary |
| i | serial number of hydraulic fractures |
| ω | wellbore |
References
- Soliman, M.; Daal, J.; East, L. Fracturing unconventional formations to enhance productivity. J. Nat. Gas Sci. Eng. 2012, 8, 52–67. [Google Scholar] [CrossRef]
- Nguyen-Le, V.; Shin, H. Development of reservoir economic indicator for Barnett Shale gas potential evaluation based on the reservoir and hydraulic fracturing parameters. J. Nat. Gas Sci. Eng. 2019, 66, 159–167. [Google Scholar] [CrossRef]
- Dian, F.; Amin, E. Semi-analytical modeling of shale gas flow through fractal induced fracture networks with micro-seismic data. Fuel 2017, 193, 444–459. [Google Scholar]
- Fan, D.Y.; Yao, J.; Sun, H.; Zeng, H.; Wang, W. A composite model of hydraulic fractured horizontal well with stimulated reservoir volume in tight oil & gas reservoir. J. Nat. Gas Sci. Eng. 2015, 24, 115–123. [Google Scholar]
- Zhao, Y.; Zhang, L.-H.; Luo, J.-X.; Zhang, B.-N. Performance of fractured horizontal well with stimulated reservoir volume in unconventional gas reservoir. J. Hydrol. 2014, 512, 447–456. [Google Scholar] [CrossRef]
- Brown, M.; Ozkan, E.; Ragahavan, R.; Kazemi, H. Practical solutions for pressure transient responses of fractured horizontal wells in unconventional reservoirs. SPE Res. Eval. Eng. 2011, 14, 663–676. [Google Scholar] [CrossRef]
- Stalgorova, E.; Mattar, L. Practical analytical model to simulate production of horizontal wells with branch fractures. In Proceedings of the SPE Paper 162515 Presented at SPE Canadian Unconventional Resources Conference, Calgary, AB, Canada, 30 October–1 November 2012. [Google Scholar]
- Stalgorova, K.; Mattar, L. Analytical model for unconventional multi-fractured composite systems. SPE Reserv. Eval. Eng. 2013, 16, 246–256. [Google Scholar] [CrossRef]
- Guo, J.; Zeng, J.; Wang, X. Analytical model for multi-fractured horizontal wells in heterogeneous shale reservoirs. In Proceedings of the SPE Asia Pacific Oil & Gas Conference and Exhibition, Society of Petroleum Engineers (SPE), Perth, Australia, 25–27 October 2016. [Google Scholar]
- Ozcan, O.; Sarak, H.; Ozkan, E.; Raghavan, R. A trilinear flow model for a fractured horizontal well in a fractal unconventional reservoir. In Proceedings of the SPE Paper 170971 Presented at SPE Annual Technical Conference and Exhibition, Amsterdam, The Netherlands, 27–29 October 2014. [Google Scholar]
- Wang, W.; Su, Y.; Sheng, G.; Cossio, M.; Shang, Y. A mathematical model considering complex fractures and fractal flow for pressure transient analysis of fractured horizontal wells in unconventional reservoirs. J. Nat. Gas Sci. Eng. 2015, 23, 139–147. [Google Scholar] [CrossRef]
- Salam, A.R.; Tiab, D. Partially penetrating hydraulic fractures: Pressure responses and flow dynamics. In Proceedings of the SPE Paper 164500 Presented at SPE Production and Operation Symposium, Oklahoma City, OK, USA, 23–26 March 2013. [Google Scholar]
- Zawila, J.; Fluckiger, S.; Hughes, G.; Kerr, P.; Hennes, A.; Hofmann, M. An integrated, multi-disciplinary approach utilizing stratigraphy, petro-physics, and geophysics to predict reservoir properties of tight unconventional sandstones in the Powder River basin, Wyoming, USA. In Proceedings of the SEG Paper 5852423 Presented at SEG Annual Meeting, New Orleans, LA, USA, 19–20 August 2015. [Google Scholar]
- Liu, P.; Ju, Y.; Ranjith, P.G.; Zheng, Z.; Chen, J. Experimental investigation of the effects of heterogeneity and geostress difference on the 3D growth and distribution of hydro-fracturing cracks in unconventional reservoir rocks. J. Nat. Gas Sci. Eng. 2016, 35, 541–554. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Durlofsky, L.J.; Aziz, K. An efficient Discrete-Fracture model applicable for general-purpose reservoir simulators. In Proceedings of the SPE Paper 79699 Presented at SPE Reservoir Simulation Symposium, Houston, TX, USA, 3–5 February 2004. [Google Scholar]
- Warpinski, N.; Mayerhofer, M.; Vincent, M.; Cipolla, C.; Lolon, E. Stimulating Unconventional Reservoirs: Maximizing Network Growth While Optimizing Fracture Conductivity. J. Can. Pet. Technol. 2009, 48, 39–51. [Google Scholar] [CrossRef]
- Yan, X.; Huang, Z.; Yao, J.; Li, Y.; Fan, D. An efficient embedded discrete fracture model based on mimetic finite difference method. J. Pet. Sci. Eng. 2016, 145, 11–21. [Google Scholar] [CrossRef]
- Gringarten, A.C.; Ramey, H.J. The Use of Source and Green’s Functions in Solving Unsteady-Flow Problems in Reservoirs. Soc. Pet. Eng. J. 1973, 13, 285–296. [Google Scholar] [CrossRef]
- Chen, C.-C.; Rajagopal, R. A Multiply-Fractured Horizontal Well in a Rectangular Drainage Region. SPE J. 1997, 2, 455–465. [Google Scholar] [CrossRef]
- Guo, G.; Evans, R.D. Pressure-transient behavior and inflow performance of horizontal wells intersecting discrete fractures. In Proceedings of the SPE paper 26446 Presented at SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1993. [Google Scholar]
- Ozkan, E.; Raghavan, R. New Solutions for Well-Test-Analysis Problems: Part 1-Analytical Considerations (includes associated papers 28666 and 29213 ). SPE Form. Eval. 1991, 6, 359–368. [Google Scholar] [CrossRef] [Green Version]
- Özkan, E.; Raghavan, R. New Solutions for Well-Test-Analysis Problems: Part 2 Computational Considerations and Applications. SPE Form. Eval. 1991, 6, 369–378. [Google Scholar] [CrossRef]
- Jia, P.; Cheng, L.; Huang, S.; Wu, Y. A semi-analytical model for the flow behavior of naturally fractured formations with multi-scale fracture networks. J. Hydrol. 2016, 537, 208–220. [Google Scholar] [CrossRef]
- Zerzar, A.; Bettam, Y. Interpretation of multiple hydraulically fractured horizontal wells in closed systems. In Proceedings of the SPE Paper 84888 Presented at SPE International Improved Oil Recovery Conference in Asia Pacific, Kuala Lumpur, Malaysia, 8–10 June 2003. [Google Scholar]
- Zhao, Y.; Zhang, L.-H.; Zhao, J.-Z.; Luo, J.-X.; Zhang, B.-N. “Triple porosity” modeling of transient well test and rate decline analysis for multi-fractured horizontal well in shale gas reservoirs. J. Pet. Sci. Eng. 2013, 110, 253–262. [Google Scholar] [CrossRef]
- Xu, J.; Guo, C.; Wei, M.; Jiang, R. Production performance analysis for composite shale gas reservoir considering multiple transport mechanisms. J. Nat. Gas Sci. Eng. 2015, 26, 382–395. [Google Scholar] [CrossRef]
- Zeng, H.; Fan, D.; Yao, J.; Sun, H. Pressure and rate transient analysis of composite shale gas reservoirs considering multiple mechanisms. J. Nat. Gas Sci. Eng. 2015, 27, 914–925. [Google Scholar] [CrossRef]
- Kikani, J.; Horne, R.N. Modeling Pressure-Transient Behavior of Sectionally Homogeneous Reservoirs by the Boundary-Element Method. SPE Form. Eval. 1993, 8, 145–152. [Google Scholar] [CrossRef]
- Idorenyin, E.H.; Shirif, E. Transient response in arbitrary-shaped composite reservoirs. SPE Res. Eval. Eng. 2016, 9, 1–13. [Google Scholar] [CrossRef]
- Medeiros, F.; Özkan, E.; Kazemi, H. A Semianalytical Approach to Model Pressure Transients in Heterogeneous Reservoirs. SPE Reserv. Eval. Eng. 2010, 13, 341–358. [Google Scholar] [CrossRef]
- Mayerhofer, M.J.; Lolon, E.; Warpinski, N.R.; Cipolla, C.L.; Walser, D.W.; Rightmire, C.M. What Is Stimulated Reservoir Volume? SPE Prod. Oper. 2010, 25, 89–98. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Yaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1959. [Google Scholar]
- Stehfest, H. Numerical Inversion of Laplace Transforms. Commun. ACM 1970, 13, 47–49. [Google Scholar] [CrossRef]









| Parameters | Value | Unit |
|---|---|---|
| Reference length, ℓ | 100 | m |
| Hydraulic fracture number | 3 | - |
| Reservoir size in x, y-direction xe, ye | 1200 | m |
| Each block size in x, y direction, xei, yei | 400 | m |
| Half-length of each hydraulic fracture, Lfi | 60 | m |
| Formation thickness, h | 100 | m |
| hydraulic fracture height, hfi | 100 | m |
| Natural fracture permeability, kfi | 100 | mD |
| Matrix Permeability, km | 1 | mD |
| Initial pressure | 35 | MPa |
| elastic storage ratio ωfi | 0.1 | - |
| crossflow coefficient λfi | 2 | - |
| tD | Zerar 2004 | me = 1 | me = 2 | me = 3 | me = 4 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| pD | dpD/dlntD | pD | dpD/dlntD | pD | dpD/dlntD | pD | dpD/dlntD | pD | dpD/dlntD | |
| 0.001 | 0.031139 | 0.016465 | 0.031139 | 0.016465 | 0.031139 | 0.016465 | 0.031139 | 0.016465 | 0.031139 | 0.016465 |
| 0.01 | 0.098465 | 0.052051 | 0.098465 | 0.052051 | 0.098465 | 0.052051 | 0.098465 | 0.052051 | 0.098465 | 0.052051 |
| 0.1 | 0.298781 | 0.138895 | 0.298781 | 0.138895 | 0.298781 | 0.138895 | 0.298781 | 0.138895 | 0.298781 | 0.138895 |
| 1 | 0.644286 | 0.184087 | 0.644049 | 0.183229 | 0.644049 | 0.183229 | 0.644049 | 0.183229 | 0.644049 | 0.183229 |
| 10 | 1.289051 | 0.50975 | 1.285585 | 0.509678 | 1.285585 | 0.509678 | 1.285585 | 0.509678 | 1.285585 | 0.509678 |
| 100 | 5.237377 | 4.36373 | 5.237641 | 4.366273 | 5.237641 | 4.366273 | 5.237641 | 4.366273 | 5.237641 | 4.366273 |
| 1000 | 44.5198 | 43.70941 | 44.53383 | 43.78088 | 44.53383 | 43.78088 | 44.53383 | 43.78088 | 44.53383 | 43.78088 |
| 10,000 | 437.4155 | 437.3679 | 437.1711 | 435.6028 | 437.1711 | 435.6028 | 437.1711 | 435.6028 | 437.1711 | 435.6028 |
| Errors | - | - | 0.0664% | 0.2043% | 0.0654% | 0.2003% | 0.065% | 0.2001% | 0.065% | 0.2001% |
| Parameters | Case 1 | Case 2 | Case 3 | Case 4 | Case 5 |
|---|---|---|---|---|---|
| 1:1:1 | 1:2:1 | 1:1/2:1 | 1:2:3 | 1:1/2:1/4 | |
| 1:1:1 | 1:2:1 | 1:1/2:1 | - | - | |
| 1:1:1 | 1:2:1 | 1:2:3 | - | - | |
| 1:1:1 | 1:2:1 | 1:2:3 | - | - | |
| 1:1:1 | 1:2:1 | 2:1:2 | - | - |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, D.; Sun, H.; Yao, J.; Zeng, H.; Yan, X.; Sun, Z. Pressure-Transient Performances of Fractured Horizontal Wells in the Compartmentalized Heterogeneous Unconventional Reservoirs. Energies 2020, 13, 5204. https://doi.org/10.3390/en13195204
Fan D, Sun H, Yao J, Zeng H, Yan X, Sun Z. Pressure-Transient Performances of Fractured Horizontal Wells in the Compartmentalized Heterogeneous Unconventional Reservoirs. Energies. 2020; 13(19):5204. https://doi.org/10.3390/en13195204
Chicago/Turabian StyleFan, Dongyan, Hai Sun, Jun Yao, Hui Zeng, Xia Yan, and Zhixue Sun. 2020. "Pressure-Transient Performances of Fractured Horizontal Wells in the Compartmentalized Heterogeneous Unconventional Reservoirs" Energies 13, no. 19: 5204. https://doi.org/10.3390/en13195204
APA StyleFan, D., Sun, H., Yao, J., Zeng, H., Yan, X., & Sun, Z. (2020). Pressure-Transient Performances of Fractured Horizontal Wells in the Compartmentalized Heterogeneous Unconventional Reservoirs. Energies, 13(19), 5204. https://doi.org/10.3390/en13195204