Three-Dimensional Imaging and Quantification of Gas Storativity in Nanoporous Media via X-rays Computed Tomography
Abstract
:1. Introduction
2. Computed Tomography (CT)
Diagnostic Methods
3. Sample Preparation
4. Experimental Procedure
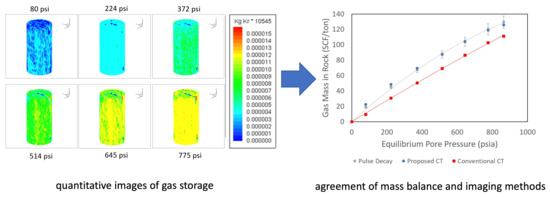
5. Results
Krypton Storativity via CT
6. Summary
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| PD | Pulse decay |
| SCF | Standard cubic feet |
| HU | Hounsfield units |
| CT | Computed tomography |
| Z | Real gas compressibility factor |
| Pore pressure | |
| T | Temperature |
| R | Universal gas constant |
| Kr molecular weight | |
| Apparent Kr pore volume | |
| Total number of voxels in imaged rock | |
| Apparent Kr porosity | |
| Rock storativity | |
| Atmospheric pressure | |
| Voxel volume | |
| Voxel-by-voxel Kr mass | |
| Number of voxels per slice | |
| Kr mass in each slice | |
| Number of slices | |
| Total Kr mass in imaged rock | |
| Mass of imaged rock | |
| Bulk rock density | |
| Voxel-by-voxel Kr density | |
| Slope of Kr CT number versus Kr density | |
| Atomic weight | |
| Density | |
| Energy of the incident photon beam | |
| Constant that depends on the electron shell | |
| Effective atomic number | |
| CT number of Kr saturated rock | |
| CT number of dry rock | |
| CT number of pure Kr | |
| CT number of air | |
| Linear attenuation coefficient of water | |
| Linear attenuation coefficient of air | |
| Linear attenuation coefficient of sample x |
References
- McGlade, C.; Speirs, J.; Sorrell, S. Methods of estimating shale gas resources—Comparison, evaluation and implications. Energy 2013, 59, 116–125. [Google Scholar] [CrossRef] [Green Version]
- Zheng, J.; Wang, Z.; Gong, W.; Ju, Y.; Wang, M. Characterization of nanopore morphology of shale and its effects on gas permeability. J. Nat. Gas Sci. Eng. 2017, 47, 83–90. [Google Scholar] [CrossRef]
- Li, C.; Carman, P.S.; Davis, B.J. Modern Fracturing Revitalizes Dormant Technologies: A Case History. Soc. Pet. Eng. 2018. [Google Scholar] [CrossRef]
- Sinal, M.L.; Lancaster, G. Liquid CO Fracturing: Advantages And Limitations. Pet. Soc. Canada. 1987. [Google Scholar] [CrossRef]
- Gupta, D.V.S. Unconventional Fracturing Fluids for Tight Gas Reservoirs. Soc. Pet. Eng. 2009. [Google Scholar] [CrossRef]
- Wu, W.; Sharma, M.M. Acid Fracturing in Shales: Effect of Dilute Acid on Properties and Pore Structure of Shale. Soc. Pet. Eng. 2017. [Google Scholar] [CrossRef]
- Clarkson, C.; Solano, N.; Bustin, R.; Bustin, A.; Chalmers, G.; He, L.; Melnichenko, Y.; Radliński, A.; Blach, T. Pore structure characterization of North American shale gas reservoirs using USANS/SANS, gas adsorption, and mercury intrusion. Fuel 2013, 103, 606–616. [Google Scholar] [CrossRef]
- Bustin, R.M.; Bustin, A.M.M.; Cui, A.; Ross, D.; Pathi, V.M. Impact of Shale Properties on Pore Structure and Storage Characteristics. Soc. Pet. Eng. 2008. [Google Scholar] [CrossRef]
- Clarkson, C.R.; Jensen, J.L.; Blasingame, T. Reservoir Engineering for Unconventional Reservoirs: What Do We Have to Consider? Soc. Pet. Eng. 2011. [Google Scholar] [CrossRef]
- Greene, J.; Viamontes, J.; Hill, B. The Connected Pore Space Paradigm: An Evaluation of the Effect of Crushing on Pore Volume and Structure. Unconv. Resour. Technol. Conf. 2020. [Google Scholar] [CrossRef]
- Aljamaan, H.; Alnoaimi, K.; Kovscek, A.R. In-Depth Experimental Investigation of Shale Physical and Transport Properties. Unconv. Resour. Technol. Conf. 2013. [Google Scholar] [CrossRef]
- Alnoaimi, K.R.; Duchateau, C.; Kovscek, A.R. Characterization and Measurement of Multiscale Gas Transport in Shale-Core Samples. Soc. Pet. Eng. 2016. [Google Scholar] [CrossRef]
- Eliebid, M.; Mahmoud, M.; Al-Yousef, H.Y.; Elkatatny, S.; Al-Garadi, K. Effect of Gas Adsorption on Pulse-Decay Permeability Measurements. Soc. Pet. Eng. 2018. [Google Scholar] [CrossRef]
- Cui, X.; Bustin, A.M.; Bustin, R.M. Measurements of gas permeability and diffusivity of tight reservoir rocks: Different approaches and their applications. Geofluids 2009, 9, 208–223. [Google Scholar] [CrossRef]
- Glatz, G.; Castanier, L.M.; Kovscek, A.R. Visualization and Quantification of Thermally Induced Porosity Alteration of Immature Source Rock Using X-ray Computed Tomography. Energy Fuels 2016, 30, 8141–8149. [Google Scholar] [CrossRef]
- Vega, B.; Dutta, A.; Kovscek, A.R. CT Imaging of Low-Permeability, Dual-Porosity Systems Using High X-ray Contrast Gas. Transp. Porous Media 2014, 101, 81–97. [Google Scholar] [CrossRef]
- Fogden, A.; Goergen, E.; Olson, T.; Cheng, Q.; Middleton, J.; Kingston, A.; Jernigen, J. Applications of Multi-Scale Imaging Techniques to Unconventional Reservoirs. Soc. Pet. Eng. 2015. [Google Scholar] [CrossRef]
- Joss, L.; Pini, R. Digital Adsorption: 3D Imaging of Gas Adsorption Isotherms by X-rays Computed Tomography. J. Phys. Chem. C 2017, 121, 26903–26915. [Google Scholar] [CrossRef] [Green Version]
- Meng, X.; Sheng, J.J.; Yu, Y. Experimental and Numerical Study of Enhanced Condensate Recovery by Gas Injection in Shale Gas-Condensate Reservoirs. Soc. Pet. Eng. 2017. [Google Scholar] [CrossRef]
- Lu, X.C.; Pepin, G.P.; Moss, R.M.; Watson, A.T. Determination of Gas Storage in Devonian Shales With X-Ray-Computed Tomography. Soc. Pet. Eng. 1992. [Google Scholar] [CrossRef]
- Alnoaimi, K.; Kovscek, A.R. Influence of Microcracks on Flow and Storage Capacities of Gas Shales at Core Scale. Transp. Porous Media 2018, 127, 53–84. [Google Scholar] [CrossRef]
- Huo, D.; Benson, S. Experimental Investigation of Stress-Dependency of Relative Permeability in Rock Fractures. Transp. Porous Media 2016, 113, 567–590. [Google Scholar] [CrossRef]
- Huo, D.; Pini, R.; Benson, S.M. A calibration-free approach for measuring fracture aperture distributions using X-rays computed tomography. Geosphere 2016, 12, 558–571. [Google Scholar] [CrossRef]
- Elkady, Y.; Kovscek, A.R. Multiscale study of CO2 impact on fluid transport and carbonate dissolution in Utica and Eagle Ford shale. J. Pet. Sci. Eng. 2020, 195, 107867. [Google Scholar] [CrossRef]
- Akin, S.; Kovscek, A.R. Computed tomography in petroleum engineering research. Geol. Soc. Lond. Spec. Publ. 2003, 215, 23–38. [Google Scholar] [CrossRef]
- Vinegar, H.J.; Wellington, S.L. Tomographic imaging of three phase flow experiments. Rev. Sci. Instrum. 1987, 58, 96–107. [Google Scholar] [CrossRef]
- McCullough, E.C. Photon attenuation in computed tomography. Med. Phys. 1975, 2, 307. [Google Scholar] [CrossRef]
- Withjack, E.M. Computed Tomography for Rock-Property Determination and Fluid-Flow Visualization. Soc. Pet. Eng. 1998. [Google Scholar] [CrossRef]
- Alnoaimi, K.R. Influence of Cracks and Microcracks on Flow and Storage Capacities of Gas Shales at Core-Level. Ph.D. Thesis, Stanford Univerisity, Stanford, CA, USA, 2016. [Google Scholar]
- Aljamaan, H.; Ross, C.M.; Kovscek, A.R. Multiscale Imaging of Gas Adsorption in Shales. Soc. Pet. Eng. 2017. [Google Scholar] [CrossRef]
- Buzug, T. Computed Tomography: From Photon Statistics to Modern Cone-Beam CT; Springer: Berlin/Heidelberg, Germany, 2008; 522p. [Google Scholar] [CrossRef]
- Elkady, Y.; Kovscek, A.R. Laboratory Visualization of Enhanced Gas Recovery in Shale, Manuscript No. SPE-201707-MS Submitted and Accepted for ATCE 2020; Society of Petroleum Engineers: Richardson, TX, USA, 2020.
- Lyu, Y.; Dasani, D.; Tsotsis, T.; Jessen, K. Characterization of Shale using Helium and Argon at High Pressures. J. Pet. Sci. Eng. 2020. submitted for review. [Google Scholar]








| Sample | TOC | Clay | Carbonates | Quartz | Feldspar | Pyrite | Plagioclase/Chlorite |
|---|---|---|---|---|---|---|---|
| Eagle Ford | 18 | 0 | |||||
| Wolfcamp | 25 | 15 | 50 | ||||
| Pressure (Psia) | PD (%) | Conventional CT (%) | New CT (%) |
|---|---|---|---|
| 216 | |||
| 397 | |||
| 556 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elkady, Y.; Lyu, Y.; Jessen, K.; Kovscek, A.R. Three-Dimensional Imaging and Quantification of Gas Storativity in Nanoporous Media via X-rays Computed Tomography. Energies 2020, 13, 6199. https://doi.org/10.3390/en13236199
Elkady Y, Lyu Y, Jessen K, Kovscek AR. Three-Dimensional Imaging and Quantification of Gas Storativity in Nanoporous Media via X-rays Computed Tomography. Energies. 2020; 13(23):6199. https://doi.org/10.3390/en13236199
Chicago/Turabian StyleElkady, Youssef, Ye Lyu, Kristian Jessen, and Anthony R. Kovscek. 2020. "Three-Dimensional Imaging and Quantification of Gas Storativity in Nanoporous Media via X-rays Computed Tomography" Energies 13, no. 23: 6199. https://doi.org/10.3390/en13236199
APA StyleElkady, Y., Lyu, Y., Jessen, K., & Kovscek, A. R. (2020). Three-Dimensional Imaging and Quantification of Gas Storativity in Nanoporous Media via X-rays Computed Tomography. Energies, 13(23), 6199. https://doi.org/10.3390/en13236199