Nonlinear Characteristics Compensation of Inverter for Low-Voltage Delta-Connected Induction Motor
Abstract
:1. Introduction
2. Nonlinear Characteristics of the Inverter for Low-Voltage Electric Vehicles
2.1. Dead-time and Turn-on/off Delay
2.2. Voltage Drop Across the MOSFET
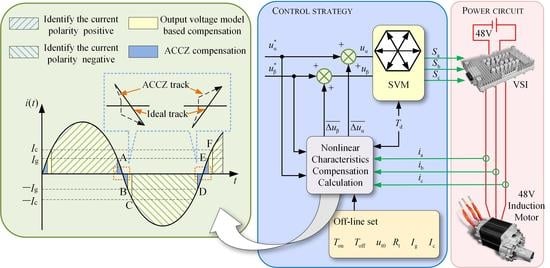
3. The Proposed Compensation Scheme
3.1. Compensation based on the Output Voltage Model of VSI
3.2. Advancing Current Crossing Zero (ACCZ) Compensation
3.3. A combination of Two Compensation Modes
4. Experimental Verification
5. Conclusions
- Compensation according to the VSI output voltage model with consideration of the conducting properties of MOSFET has a better effect than the common compensation method.
- ACCZ compensation not only avoids the complicated calculations required for current polarity, but also effectively inhibits the current waveform distortion near current zero.
- The proposed compensation scheme based on the combination of the output voltage model and ACCZ is suitable for nonlinear characteristics compensation for VSIs for low-voltage, delta-connected IMs.
Author Contributions
Funding
Conflicts of Interest
References
- Wearing, A.D.; Haybittle, J.; Bao, R.; Baxter, J.W.; Rouaud, C.; Taskin, O. Development Of High Power 48V Powertrain Components For Mild Hybrid Light Duty Vehicle Applications. In Proceedings of the 2018 IEEE Energy Conversion Congress and Exposition, Portland, OR, USA, 23–27 September 2018; pp. 3893–3900. [Google Scholar]
- Ferreira, F.J.T.E.; Silva, A.M.; Cruz, S.M.A.; De Almeida, A.T. Comparison of Losses in Star- and Delta-Connected Induction Motors with Saturated Core. In Proceedings of the 2017 IEEE International Electric Machines and Drives Conference, Miami, FL, USA, 21–24 May 2017. [Google Scholar]
- Lee, K.; Yao, W.; Chen, B.; Lu, Z.; Yu, A.; Li, D. Stability Analysis and Mitigation of Oscillation in an Induction Machine. IEEE Trans. Ind. Appl. 2014, 50, 3767–3776. [Google Scholar] [CrossRef]
- Guha, A.; Narayanan, G. Impact of Undercompensation and Overcompensation of Dead-Time Effect on Small-Signal Stability of Induction Motor Drive. IEEE Trans. Ind. Appl. 2018, 54, 6027–6041. [Google Scholar] [CrossRef]
- Li, P.; Zhang, L.; Ouyang, B.; Liu, Y. Nonlinear Effects of Three-Level Neutral-Point Clamped Inverter on Speed Sensorless Control of Induction Motor. Electronics 2019, 8, 402. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Wu, Q.M.J.; Kawamura, A. An accurate approach of nonlinearity compensation for VSI inverter output voltage. IEEE Trans. Power Electron. 2004, 19, 1029–1035. [Google Scholar] [CrossRef]
- Park, D.; Kim, K. Parameter-Independent Online Compensation Scheme for Dead Time and Inverter Nonlinearity in IPMSM Drive Through Waveform Analysis. IEEE Trans. Ind. Electron. 2014, 61, 701–707. [Google Scholar] [CrossRef]
- Ben-Brahim, L.; Gastli, A.; Ghazi, K. Implementation of Iterative Learning Control based Deadtime Compensation for PWM Inverters. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications, Geneva, Switzerland, 8–10 September 2015. [Google Scholar]
- Ahmed, S.; Shen, Z.; Mattavelli, P.; Boroyevich, D.; Karimi, K.J. Small-Signal Model of Voltage Source Inverter (VSI) and Voltage Source Converter (VSC) Considering the DeadTime Effect and Space Vector Modulation Types. IEEE Trans. Power Electron. 2017, 32, 4145–4156. [Google Scholar] [CrossRef]
- Munoz, A.R.; Lipo, T.A. On-line dead-time compensation technique for open-loop PWM-VSI drives. IEEE Trans. Power Electron. 1999, 14, 683–689. [Google Scholar] [CrossRef] [Green Version]
- Zhang, L.; Yuan, X.; Zhang, J.; Wu, X.; Zhang, Y.; Wei, C. Modeling and Implementation of Optimal Asymmetric Variable Dead-Time Setting for SiC MOSFET-Based Three-Phase Two-Level Inverters. IEEE Trans. Power Electron. 2019, 34, 11645–11660. [Google Scholar] [CrossRef]
- Lee, D.; Ahn, J. A Simple and Direct Dead-Time Effect Compensation Scheme in PWM-VSI. IEEE Trans. Ind. Appl. 2014, 50, 3017–3025. [Google Scholar] [CrossRef]
- Tang, Z.; Akin, B. A New LMS Algorithm Based Deadtime Compensation Method for PMSM FOC Drives. IEEE Trans. Ind. Appl. 2018, 54, 6472–6484. [Google Scholar] [CrossRef]
- Buchta, L.; Otava, L. Adaptive Compensation of Inverter Non-linearities Based on the Kalman Filter. In Proceedings of the Iecon 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 4301–4306. [Google Scholar]
- Yang, K.; Yang, M.; Lang, X.; Lang, Z.; Xu, D. An Adaptive Dead-time Compensation Method based on Predictive Current Control. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference, Hefei, China, 22–26 May 2016; pp. 121–125. [Google Scholar]
- Tang, Z.; Akin, B. Compensation of Dead-Time Effects Based on Revised Repetitive Controller for PMSM Drives. In Proceedings of the 2017 Thirty Second Annual Ieee Applied Power Electronics Conference and Exposition, Tampa, FL, USA, 26–30 March 2017; pp. 2730–2737. [Google Scholar]
- Buchta, L. Online Adaptive Compensation Scheme for Dead-Time and Inverter Nonlinearity in PMSM Drive. In Proceedings of the 14th IFAC Conference on Programmable Devices and Embedded Systems (PDES), Brno, Czech Republic, 5–7 October 2016; pp. 43–48. [Google Scholar]
- Chierchie, F.; Paolini, E.E.; Stefanazzi, L. Dead-Time Distortion Shaping. IEEE Trans. Power Electron. 2019, 34, 53–63. [Google Scholar] [CrossRef]
- Wang, Y.; Xie, W.; Wang, X.; Gerling, D. A Precise Voltage Distortion Compensation Strategy for Voltage Source Inverters. IEEE Trans. Ind. Electron. 2018, 65, 59–66. [Google Scholar] [CrossRef]
- Sun, W.; Gao, J.; Liu, X.; Yu, Y.; Wang, G.; Xu, D. Inverter Nonlinear Error Compensation Using Feedback Gains and Self-Tuning Estimated Current Error in Adaptive Full-Order Observer. IEEE Trans. Ind. Appl. 2016, 52, 472–482. [Google Scholar] [CrossRef]
- Mitsubishi. MOSFET Modules Application Note. Available online: http://www.mitsubishielectric-mesh.com/download/document/20150727gBvTi.pdf (accessed on 28 December 2019).
- Mitsubishi. Using IGBT Modules. Available online: http://www.mitsubishielectric-mesh.com/download/app/gonglv.php (accessed on 28 December 2019).
- Lin, Y.; Lai, Y. Dead-Time Elimination of PWM-Controlled Inverter/Converter Without Separate Power Sources for Current Polarity Detection Circuit. IEEE Trans. Ind. Electron. 2009, 56, 2121–2127. [Google Scholar]










| Parameters | Value |
|---|---|
| Rated voltage/frequency/power | 48 V/50 Hz/15 kW |
| Rated torque/speed | 20 (N·m)/1500 (r/min) |
| Stator resistance/Rotor resistance | 0.00718065 Ω/0.00839509 Ω |
| Stator leakage inductance | 3.6284 × 10−5 H |
| Rotor leakage inductance | 2.75251 × 10−5 H |
| Excitation inductance | 0.00112 H |
| Rotational inertia | 0.0164(kg·m2) |
| Pole-pairs | 2 |
| Voltage Set and Compensation Kind | THD |
|---|---|
| 5 V/5 Hz and no compensation | 19.33% |
| 5 V/5 Hz and common compensation | 13.53% |
| 5 V/5 Hz and proposed compensation | 12.71% |
| 30 V/5 Hz and no compensation | 15.78% |
| 30 V/5 Hz and common compensation | 10.84% |
| 30 V/5 Hz and proposed compensation | 7.62% |
| 30 V/30 Hz and no compensation | 6.62% |
| 30 V/30 Hz and common compensation | 4.37% |
| 30 V/30 Hz and proposed compensation | 2.82% |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, Q.; Dong, Z.; Liu, H.; You, X. Nonlinear Characteristics Compensation of Inverter for Low-Voltage Delta-Connected Induction Motor. Energies 2020, 13, 590. https://doi.org/10.3390/en13030590
Guo Q, Dong Z, Liu H, You X. Nonlinear Characteristics Compensation of Inverter for Low-Voltage Delta-Connected Induction Motor. Energies. 2020; 13(3):590. https://doi.org/10.3390/en13030590
Chicago/Turabian StyleGuo, Qiang, Zhiping Dong, Heping Liu, and Xiaoyao You. 2020. "Nonlinear Characteristics Compensation of Inverter for Low-Voltage Delta-Connected Induction Motor" Energies 13, no. 3: 590. https://doi.org/10.3390/en13030590
APA StyleGuo, Q., Dong, Z., Liu, H., & You, X. (2020). Nonlinear Characteristics Compensation of Inverter for Low-Voltage Delta-Connected Induction Motor. Energies, 13(3), 590. https://doi.org/10.3390/en13030590