Power System Nonlinear Modal Analysis Using Computationally Reduced Normal Form Method
Abstract
:1. Introduction
2. Normal Form Theory
2.1. Indices for Modal Interaction
2.1.1. Nonlinearity Indices
2.1.2. Nonlinear Interaction Indices
2.1.3. Nonlinear Modal Persistence Indices
2.2. Normal Form Initial Condition
- Define , the initial condition of the power system after disturbance as , where is the post disturbance equilibrium solution and is the system condition at the end of the disturbance.
- Use the eigenvector to obtain the initial condition in Jordan coordinate as .
- To compute
- I.
- Formulate the solution problem as (8).
- II.
- Choose the initial guess for . recommended.
- III.
- Compute the mismatch function for iteration s as:
- IV.
- Compute the Jacobian of at as
- V.
- Compute the increment
- VI.
- Obtain the optimal step length with cubic interpolation or any other appropriate procedure and compute .
- VII.
- Iterate till a specific tolerance is met. The value of meeting the tolerance gives the solution .
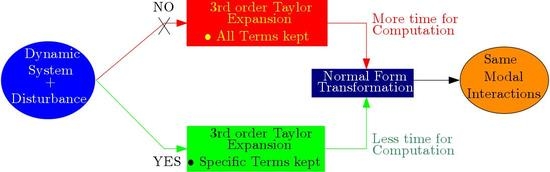
3. Proposed Normal Form Computation Reduction
- A combination of only real modes does not lead to new frequency in the spectral.
- A 2nd order combination of a real mode with an oscillatory mode does not lead to new frequency in the spectral, rather a more damped version of the oscillatory mode which combined with the real mode.
- A 3rd order combination of real and oscillatory modes may lead to a new frequency but this frequency must be the more damped version of a combination of two oscillatory modes already existing at 2nd order.
4. Numerical Simulations and Results
4.1. System Description
Case 1: Fault cleared after 0.019s. This case represents a less stressed condition.
Case 2: Fault cleared after 0.184s which is almost the critical clearing time (Critical clearing time is 0.185 s). This case represents stressed condition with severe nonlinear behaviour.
4.2. Reduced Model
4.3. Analysis of Case 1
4.4. Analysis of Case 2
Qualitative NF Analysis of Case 2
4.5. Relevance of NF Modal Interaction in Power System Control Designs
5. Discussion
- The results illustrate that the proposed method can significantly reduce the computational burden in NF applications. This is depicted with the pie chart shown in Figure 2, where the computation time using the proposed method occupies a sector of 30% against the conventional technique which occupies 70%. In [6], 2nd order modal interaction was studied with a model that has 27 eigenvalues of which 13 are real. In the interpretation of the results, the interactions involving real modes were ignored, which implies a huge computational waste. If this model is to be considered for 3rd order NF study, it will generate 108,864 coefficients. However, with the proposed method, this model will only have 9310 coefficients, a computational saving factor of 12.
- The results show that stressed power system leads to nonlinear interactions of modes. This can be seen for example in case 1 where less severe fault led to spectrum of Figure 3b with no significant interaction, whereas in case 2 where the stress increases, the nonlinearity increases and the modal interaction becomes apparent in the spectrum of Figure 4b. NF analysis is able to identify these interactions as revealed in Table 4 and Table 5. These observations corroborate previous research on modal interaction [6]. A significant new contribution is the use of fewer terms to perform the same analysis. This contribution is especially pertinent in view of fully PE grids. In PE grids there are several modes that decay very fast. The treatment of real modes proposed in this paper may be extended to such very fast modes to further simplify NF application to PE grids.
- The results of the participation factor analyses in Figure 5a–f show the correction to the linear participation factor due to the addition of higher order terms. Reference [14] reported a case where PSS location using nonlinear participation factors outperforms the location using linear participation factor.
- As shown in Figure 5d, the combination modes may participate more than the fundamental modes. Hence, as the disturbance becomes significant, the stability/instability may not be completely determined by single eigenmodes without their interactions. Reference [5] has reported a case where single eigenvalue showed instability but the 3rd order interaction maintained the stability of the system.
- Since the idea proposed in this work addresses specific case of NF application (i.e., modal interaction) its potency for other NF applications such as stability studies is not guaranteed.
- The results indicate that avoiding the interactions associated to the real modes does not compromise the effectiveness of NF modal interaction analysis. This, however, does not mean that all other remaining interactions are nonlinearly significant.
Practical Concerns
- A major concern is the implication of the proposed method in a large system. Even with the reduction proposed in this paper, the number of nonlinear terms will still be enormous in the case of large system. It is important to state that the approach proposed here is one out of many steps needed to apply NF to large systems. As stated before, the reduction cannot be limited to interactions involving aperiodic (real) modes, but more information is needed to further the reduction to interactions involving oscillatory modes. Although general application of NF to unreduced large system remains difficult, it is good to note that the proposed reduction is based on the physics of the modes and thus, can be applied to system of any size. The authors are working on several ideas, to advance NF to large system. At the moment, reducing the network and focusing on a particular area of the network is the approach to attempt large system (already used in [44] for system with over 300 generators).
- Another valid argument could be if the usefulness of NF analysis is worth the computations involved, given that the time domain analysis could identify the interaction of nonlinear dynamics. It is good to emphasise that NF analysis just like other analytical methods, does not replace time domain analysis but complements it. Time domain analysis can identify the interactions of nonlinear dynamics but the exact natures of these interactions are unclear. Moreover, analytical parameters needed for power system control designs are not as apparent as with analytical methods. It lacks in qualitative information about the system. The nonlinear participation factor analysis helps to know from where comes the interaction. Other analytical information for the power system control designs are not exhaustively available with time domain analysis. NF analysis should be used when some phenomena are difficult to explain with the time domain analysis. Also, indices are needed based on the system condition, to know a priori that it is gainful embarking on NF analysis to avoid computational loss. These indices should be developed. The authors are optimistic that a well developed selective NF application will position it as always very useful tool.
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Abbreviations
| AVR | Automatic voltage regulator |
| DAE | Differential-algebraic equation |
| EV | Electric vehicle |
| FFT | Fast fourier transform |
| HOS | Higher order spectra |
| KMD | Koopman mode decomposition |
| LS | Least square |
| MS | Modal series |
| NF | Normal Form |
| PE | Power electronics |
| PSS | Power system stabilize |
| RE | Renewable energy |
| SEP | Stable equilibrium point |
| SSA | small-signal analysis |
References
- Un-Noor, F.; Padmanaban, S.; Mihet-Popa, L.; Mollah, M.N.; Hossain, E. A comprehensive study of key electric vehicle (EV) components, technologies, challenges, impacts, and future direction of development. Energies 2017, 10, 1217. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, M.; Saha, T.; Eghbal, M. Impact of high level of renewable energy penetration on inter-area oscillation. In Proceedings of the Australasian Universities Power Engineering Conference (AUPEC), Brisbane, QLD, Australia, 25–28 September 2011; pp. 1–6. [Google Scholar]
- You, S.; Kou, G.; Liu, Y.; Zhang, X.; Cui, Y.; Till, M.; Yao, W.; Liu, Y. Impact of High PV Penetration on the Inter-Area Oscillations in the U.S. Eastern Interconnection. IEEE Access 2017, 5, 4361–4369. [Google Scholar] [CrossRef]
- Shair, J.; Xie, X.; Wang, L.; Liu, W.; He, J.; Liu, H. Overview of emerging subsynchronous oscillations in practical wind power systems. Renew. Sustain. Energy Rev. 2019, 99, 159–168. [Google Scholar] [CrossRef]
- Tian, T.; Kestelyn, X.; Thomas, O.; Amano, H.; Messina, A.R. An Accurate Third-Order Normal Form Approximation for Power System Nonlinear Analysis. IEEE Trans. Power Syst. 2018, 33, 2128–2139. [Google Scholar] [CrossRef]
- Sanchez-Gasca, J.J.; Vittal, V.; Gibbard, M.J.; Messina, A.R.; Vowles, D.J.; Liu, S.; Annakkage, U.D. Inclusion of higher order terms for small-signal (modal) analysis: Committee report-task force on assessing the need to include higher order terms for small-signal (modal) analysis. IEEE Trans. Power Syst. 2005, 20, 1886–1904. [Google Scholar] [CrossRef] [Green Version]
- Nayfeh, A.H. The Method of Normal Forms, 2nd ed.; WILEY-VCHVerlag GmbH&Co. KGaA: Weinheim, Germany, 2011. [Google Scholar]
- Jang, G.; Vittal, V.; Kliemann, W. Effect of nonlinear modal interaction on control performance: Use of normal forms technique in control design. II. Case studies. IEEE Trans. Power Syst. 1998, 13, 401–407. [Google Scholar] [CrossRef]
- Lomei, H.; Assili, M.; Sutanto, D.; Muttaqi, K. A New Approach to Reduce the Non-Linear Characteristics of a Stressed Power System by Using the Normal Form Technique in the Control Design of the Excitation System. IEEE Trans. Ind. Appl. 2017, 53, 492–500. [Google Scholar] [CrossRef]
- Wu, F.X.; Wu, H.; Han, Z.X.; Gan, D.Q. Validation of power system non-linear modal analysis methods. Electr. Power Syst. Res. 2007, 77, 1418–1424. [Google Scholar] [CrossRef]
- Starrett, S.K. Nonlinear measures of mode-machine participation. IEEE Trans. Power Syst. 1998, 13, 389–394. [Google Scholar] [CrossRef]
- Amano, H.; Inoue, T. A New PSS Parameter Design Using Nonlinear Stability Analysis. In Proceedings of the IEEE Power Engineering Society General Meeting, Tampa, FL, USA, 24–28 June 2007; pp. 1–8. [Google Scholar]
- Liu, S.; Messina, A.R.; Vittal, V. Assessing placement of controllers and nonlinear behavior using normal form analysis. IEEE Trans. Power Syst. 2005, 20, 1486–1495. [Google Scholar] [CrossRef]
- Liu, S.; Messina, A.R.; Vittal, V. A normal form analysis approach to siting power system stabilizers (PSSs) and assessing power system nonlinear behavior. IEEE Trans. Power Syst. 2006, 21, 1755–1762. [Google Scholar] [CrossRef]
- Amano, H.; Kumano, T.; Inoue, T. Nonlinear stability indexes of power swing oscillation using normal form analysis. IEEE Trans. Power Syst. 2006, 21, 825–834. [Google Scholar] [CrossRef]
- Amano, H.; Kumano, T.; Inoue, T.; Taniguchi, H. Proposal of nonlinear stability indices of power swing oscillation in a multimachine power system. Electr. Eng. Jpn. 2005, 151, 16–24. [Google Scholar] [CrossRef]
- Martinez, I.C.; Messina, A.R.; Barocio, E. Higher-order normal form analysis of stressed power systems: A fundamental study. Electr. Power Compon. Syst. 2004, 32, 1301–1317. [Google Scholar] [CrossRef]
- Martínez, I.; Messina, A.R.; Vittal, V. Normal form analysis of complex system models: A structure-preserving approach. IEEE Trans. Power Syst. 2007, 22, 1908–1915. [Google Scholar] [CrossRef]
- Wang, B.; Sun, K.; Xu, X. Nonlinear Modal Decoupling Based Power System Transient Stability Analysis. IEEE Trans. Power Syst. 2019, 34, 4889–4899. [Google Scholar] [CrossRef]
- Saha, S.; Fouad, A.A.; Kliemann, W.H.; Vittal, V. Stability boundary approximation of a power system using the real normal form of vector fields. IEEE Power Eng. Rev. 1997, 17, 69. [Google Scholar] [CrossRef]
- Kshatriya, N.; Annakkage, U.; Gole, A.; Fernando, I. Improving the Accuracy of Normal Form Analysis. IEEE Trans. Power Syst. 2005, 20, 286–293. [Google Scholar] [CrossRef] [Green Version]
- Modir Shanechi, H.; Pariz, N.; Vaahedi, E. General Nonlinear Modal Representation of Large Scale Power Systems. IEEE Trans. Power Syst. 2003, 18, 1103–1109. [Google Scholar] [CrossRef]
- Abdollahi, A.; Pariz, N.; Shanechi, H.M. Modal series method for nonautonomous nonlinear systems. In Proceedings of the IEEE International Conference on Control Applications, Singapore, 1–3 October 2007; pp. 759–764. [Google Scholar]
- Wang, Z.; Huang, Q. A Closed Normal Form Solution under Near-Resonant Modal Interaction in Power Systems. IEEE Trans. Power Syst. 2017, 32, 4570–4578. [Google Scholar] [CrossRef]
- Netto, M.; Susuki, Y.; Mili, L. Data-Driven Participation Factors for Nonlinear Systems Based on Koopman Mode Decomposition. IEEE Control Syst. Lett. 2019, 3, 198–203. [Google Scholar] [CrossRef] [Green Version]
- Hernandez-Ortega, M.A.; Messina, A.R. Nonlinear Power System Analysis Using Koopman Mode Decomposition and Perturbation Theory. IEEE Trans. Power Syst. 2018, 33, 5124–5134. [Google Scholar] [CrossRef]
- Cossart, Q.; Colas, F.; Kestelyn, X. Model reduction of converters for the analysis of 100% power electronics transmission systems. In Proceedings of the IEEE International Conference on Industrial Technology, Lyon, France, 20–22 February 2018; pp. 1254–1259. [Google Scholar]
- MIGRATE. Horizon 2020 Work Programme 2018–2020. Available online: https://www.h2020-migrate.eu/ (accessed on 17 September 2019).
- Marinescu, B.; Mallem, B.; Rouco, L. Large-scale power system dynamic equivalents based on standard and border synchrony. IEEE Trans. Power Syst. 2010, 25, 1873–1882. [Google Scholar] [CrossRef]
- Marinescu, B.; Mallem, B.; Rouco, L. Model reduction of interconnected power systems via balanced state-space representation. In Proceedings of the 2007 European Control Conference (ECC 2007), Kos, Greece, 2–5 July 2007; pp. 4165–4172. [Google Scholar]
- Belhocine, M.; Marinescu, B. A mix balanced-modal truncations for power systems model reduction. In Proceedings of the 2014 European Control Conference (ECC 2014), Strasbourg, France, 24–27 June 2014; pp. 2721–2726. [Google Scholar]
- Ugwuanyi, N.S.; Kestelyn, X.; Thomas, O.; Marinescu, B. A Novel Method for Accelerating the Analysis of Nonlinear Behaviour of Power Grids using Normal Form Technique. In Proceedings of the Innovative Smart Grid Technologies Europe (ISGT Europe), Bucharest, Romania, 29 September–2 October 2019. [Google Scholar]
- Ugwuanyi, N.S.; Kestelyn, X.; Thomas, O.; Marinescu, B. Selective Nonlinear Coefficients Computation for Modal Analysis of The Emerging Grid. In Proceedings of the Conference des Jeunes Chercheurs en Génie Eléctrique, Ile d’Oléron, France, 11–14 June 2019. [Google Scholar]
- Messina, A.R.; Vittal, V. Assessment of nonlinear interaction between nonlinearly coupled modes using higher order spectra. IEEE Trans. Power Syst. 2005, 20, 375–383. [Google Scholar] [CrossRef]
- Wang, B.I.N.; Sun, K.A.I. Nonlinear Modal Decoupling of Multi-Oscillator Systems With Applications to Power Systems. IEEE Access 2018, 6, 9201–9217. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, Q. Study on an improved Normal Form solution and reduced-order mode reconstruction in power system. In Proceedings of the IEEE Region 10 Annual International Conference, Proceedings/TENCON, Macao, China, 1–4 November 2015. [Google Scholar]
- Ugwuanyi, N.S.; Kestelyn, X.; Thomas, O.; Marinescu, B.; Messina, A.R. A New Fast Track to Nonlinear Modal Analysis of Power System Using Normal Form. IEEE Trans. Power Syst. 2020. [Google Scholar] [CrossRef] [Green Version]
- Jang, G.; Vittal, V.; Kliemann, W. Effect of nonlinear modal interaction on control performance: Use of normal forms technique in control design. I. General theory and procedure. IEEE Trans. Power Syst. 1998, 13, 401–407. [Google Scholar] [CrossRef]
- Dobson, I.; Barocio, E. Scaling of normal form analysis coefficients under coordinate change. IEEE Trans. Power Syst. 2004, 19, 1438–1444. [Google Scholar] [CrossRef]
- Huang, Q.; Wang, Z.; Zhang, C. Evaluation of the effect of modal interaction higher than 2nd order in small-signal analysis. In Proceedings of the 2009 IEEE Power and Energy Society General Meeting, PES ’09, Calgary, AB, Canada, 26–30 July 2009; pp. 1–6. [Google Scholar]
- Sauer, P.W.; Pai, M.A. Power System Dynamics and Stability; Prentice Hall: Upper Saddle River, NJ, USA, 1998; p. 357. [Google Scholar]
- Milano, F. An open source power system analysis toolbox. IEEE Trans. Power Syst. 2005, 20, 1199–1206. [Google Scholar] [CrossRef]
- Hashlamoun, W.A.; Hassouneh, M.A.; Abed, E.H. New results on modal participation factors: Revealing a previously unknown dichotomy. IEEE Trans. Autom. Control 2009, 54, 1439–1449. [Google Scholar] [CrossRef] [Green Version]
- Vittal, V.; Kliemann, W.; Chapman, D.G.; Silk, A.D.; Xni, Y.; Sobajic, D.J. Determination of generator groupings for an islanding scheme in the manitoba hydro system using the method of normal forms. IEEE Trans. Power Syst. 1998, 13, 1345–1351. [Google Scholar] [CrossRef] [Green Version]





| Mode | Eigenvalue | Freq. | Damping | Dominant |
|---|---|---|---|---|
| # | (rad/s) | (%) | States | |
| 1 | 0 | 100 | ||
| 2 | 0 | 100 | ||
| 3 | 0 | 100 | ||
| 4,5 | ± j13.63 | 13.63 | 7.45 | |
| 6,7 | ± j8.94 | 8.94 | 1.52 | |
| 8,9 | ± j4.03 | 4.03 | 20.30 | |
| 10 | 0 | 100 | ||
| 11,12 | ± j2.86 | 2.86 | 38 | |
| 13,14 | ± j1.98 | 1.98 | 60 | |
| 15 | 0 | 100 | ||
| 16 | 0 | 100 | ||
| 17,18 | ± j0.01 | 0.01 | 99.52 | |
| 19,20 | ± j0.001 | 0.001 | 99.99 |
| Mode | Eigenvalue | N2LI | N2II |
|---|---|---|---|
| 15 | 0.315 | 0.314 | |
| 4(5) | ± j13.63 | 0.443 | 0.212 |
| 16 | 0.192 | 0.192 | |
| 17(18) | ± j0.011 | 0.139 | 0.138 |
| 13(14) | ± j1.98 | 0.245 | 0.108 |
| 10 | 0.263 | 0.100 | |
| 19(20) | ± j0.001 | 0.061 | 0.061 |
| 6(7) | ± j8.94 | 0.072 | 0.034 |
| 8(9) | ± j4.03 | 0.035 | 0.028 |
| 1 | 0.002 | 0.016 | |
| 11(12) | ± j2.86 | 0.045 | 0.014 |
| 3 | 0.015 | 0.013 | |
| 2 | 0.002 | 0.001 |
| Mode | Eigenvalue | N3LI | N3II |
|---|---|---|---|
| 16 | 0.177 | 0.069 | |
| 15 | 0.301 | 0.037 | |
| 4(5) | ± j13.63 | 0.430 | 0.016 |
| 10 | 0.250 | 0.015 | |
| 13(14) | ± j1.98 | 0.252 | 0.008 |
| 6(7) | ± j8.94 | 0.070 | 0.002 |
| 8 (9) | ± j4.03 | 0.033 | 0.002 |
| 11(12) | ± j2.86 | 0.044 | 0.001 |
| 3 | 0.015 | 0.001 | |
| 1 | 0.002 | 0.001 | |
| 17(18) | ± j0.011 | 0.143 | 0.001 |
| 19(20) | ± j0.001 | 0.061 | 0.000 |
| 2 | 0.002 | 0.000 |
| k | l | |||||
|---|---|---|---|---|---|---|
| 5.462 | 5 | 17 | − j13.62 | 0.899 | 3.529 | 4.908 |
| 1.761 | 5 | 18 | − j13.64 | 0.899 | 3.529 | 1.582 |
| 1.579 | 5 | 9 | − j17.66 | 0.549 | 2.158 | 0.868 |
| 1.539 | 5 | 8 | − j9.60 | 0.549 | 2.158 | 0.845 |
| 1.215 | 4 | 17 | + j13.64 | 0.899 | 3.529 | 1.092 |
| 1.063 | 4 | 9 | + j9.60 | 0.549 | 2.158 | 0.584 |
| 1.028 | 4 | 8 | + j17.66 | 0.549 | 2.158 | 0.565 |
| 0.308 | 4 | 5 | 0.500 | 1.964 | 0.154 | |
| 0.262 | 5 | 8 | − j9.60 | 0.549 | 2.158 | 0.144 |
| 0.258 | 7 | 9 | − j12.97 | 1.049 | 4.119 | 0.271 |
| 0.232 | 5 | 12 | − j16.50 | 0.463 | 1.820 | 0.107 |
| 0.227 | 5 | 5 | − j27.26 | 0.500 | 1.964 | 0.113 |
| 0.201 | 5 | 9 | − j17.66 | 0.549 | 2.158 | 0.110 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
| k | l | |||||
|---|---|---|---|---|---|---|
| 6.351 | 5 | 17 | − j13.62 | 0.899 | 3.529 | 5.706 |
| 2.048 | 5 | 18 | − j13.64 | 0.899 | 3.529 | 1.840 |
| 1.843 | 5 | 9 | − j17.66 | 0.549 | 2.158 | 1.013 |
| 1.798 | 5 | 8 | − j9.60 | 0.549 | 2.158 | 0.988 |
| 0.956 | 4 | 17 | + j13.64 | 0.899 | 3.529 | 0.859 |
| 0.840 | 4 | 9 | + j9.60 | 0.549 | 2.158 | 0.462 |
| 0.813 | 4 | 8 | + j17.66 | 0.549 | 2.158 | 0.447 |
| 0.307 | 5 | 5 | − j27.26 | 0.500 | 1.964 | 0.153 |
| 0.306 | 5 | 8 | − j9.60 | 0.549 | 2.158 | 0.168 |
| 0.282 | 4 | 5 | 0.500 | 1.964 | 0.141 | |
| 0.268 | 5 | 12 | − j16.50 | 0.463 | 1.820 | 0.124 |
| 0.259 | 7 | 9 | − j12.97 | 1.049 | 4.119 | 0.272 |
| 0.234 | 5 | 9 | − j17.66 | 0.549 | 2.158 | 0.129 |
| ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ | ⋯ |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ugwuanyi, N.S.; Kestelyn, X.; Marinescu, B.; Thomas, O. Power System Nonlinear Modal Analysis Using Computationally Reduced Normal Form Method. Energies 2020, 13, 1249. https://doi.org/10.3390/en13051249
Ugwuanyi NS, Kestelyn X, Marinescu B, Thomas O. Power System Nonlinear Modal Analysis Using Computationally Reduced Normal Form Method. Energies. 2020; 13(5):1249. https://doi.org/10.3390/en13051249
Chicago/Turabian StyleUgwuanyi, Nnaemeka Sunday, Xavier Kestelyn, Bogdan Marinescu, and Olivier Thomas. 2020. "Power System Nonlinear Modal Analysis Using Computationally Reduced Normal Form Method" Energies 13, no. 5: 1249. https://doi.org/10.3390/en13051249
APA StyleUgwuanyi, N. S., Kestelyn, X., Marinescu, B., & Thomas, O. (2020). Power System Nonlinear Modal Analysis Using Computationally Reduced Normal Form Method. Energies, 13(5), 1249. https://doi.org/10.3390/en13051249