Net-Metering Compared to Battery-Based Electricity Storage in a Single-Case PV Application Study Considering the Lithuanian Context
Abstract
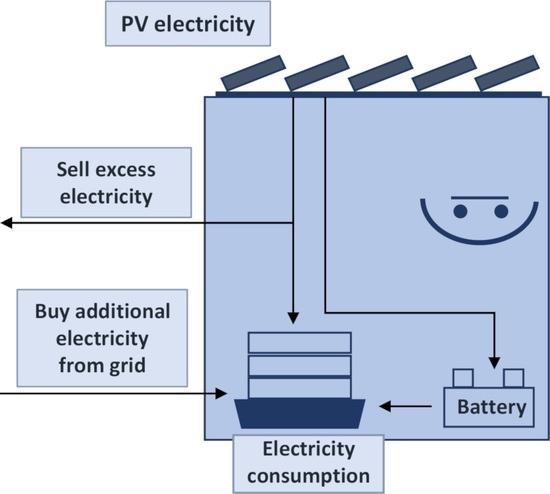
:1. Introduction
2. Study Object and Method
2.1. Study Object
- A PV system without battery storage but with net-metering (first).
- A PV system with battery storage but without net-metering (second).
- Fixed payment for energy storage at 0.042592 €/kWh (scenario I in further simulations).
- Fixed payment for the installed PV power at 2.022 €/kW/month. (scenario II).
- Mixed method that comprises payment for energy storage at 0.01938 €/kWh and payment for the installed PV power at 1.012 €/kW/month (scenario III).
- ESO uses 36% of its produced electricity to cover expenses related to energy storage and the prosumer uses 64% for its needs (scenario IV).
2.2. Simulation Method
2.2.1. Fed-In Energy Loss
2.2.2. Payback Time
2.2.3. Net Present Value (NPV)
2.2.4. Degree of Self-Sufficiency
2.2.5. Internal Rate of Return (IRR)
2.2.6. Quantified Reduction of Carbon Emissions
3. Results and Discussions
3.1. Case Study with Net-Metering
3.2. PV System with Battery Storage
- 80 kW power plant with a 4 or 8 kWh battery capacity, and
- 100 kW power plant with a 5 or 10 kWh battery capacity.
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Installed Capacity of PV/Battery Capacity (kW/kWh) | Economic Outputs | Technical Outputs | Environmental Outputs and Other Indicators | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| System Price (Thousand €) | IRR (%) | NPV (Thousand €) | Payback (Years) | Cost of Energy Purchased from the Grid (Thousand €) | Benefits from Storage System Usage (Thousand €) | Benefits from Panels Usage (Thousand €) | Solar Generation (Thousand kWh) | Cycles of the Storage System Consumed (Cycles) | Energy Bought from the Grid (Thousand kWh) | Energy Consumed from Storage System (Thousand kWh) | Energy Consumed from Panels (Thousand kWh) | Energy Exported to the Grid (Thousand kWh) | Fed-In Energy Lost (Thousand kWh) | Reduction of Carbon Emissions (Thousand kg) | Degree of Self-Sufficiency (%) | LCOE (cts/kWh) | |
| 20/5 | 16.54 | 5.8 | −0.91 | 12.0 | 1820 | 0.0 | 36.2 | 382 | 0 | 19,180 | 0.0 | 382 | 0.0 | 0.0 | 137.4 | 2.0 | 7.1 |
| 20/10 | 19.54 | 3.6 | −4.14 | 14.6 | 1821 | 0.0 | 36.2 | 381 | 0 | 19,190 | 0.0 | 381 | 0.0 | 0.0 | 137.2 | 2.0 | 7.1 |
| 20/20 | 25.54 | 0.4 | −10.58 | >20 | 1819 | 0.0 | 36.2 | 382 | 0 | 19,170 | 0.0 | 382 | 0.0 | 0.0 | 137.4 | 2.0 | 7.1 |
| 40/10 | 33.08 | 5.8 | −1.88 | 12.1 | 1781 | 0.0 | 72.3 | 762 | 0 | 18,770 | 0.0 | 762 | 0.0 | 0.0 | 274.3 | 3.9 | 7.1 |
| 40/20 | 39.08 | 3.6 | −8.34 | 14.6 | 1785 | 0.0 | 72.3 | 762 | 0 | 18,810 | 0.0 | 762 | 0.0 | 0.0 | 274.2 | 3.9 | 7.1 |
| 40/40 | 51.08 | 0.4 | −21.18 | >20 | 1784 | 0.0 | 72.5 | 764 | 0 | 18,800 | 0.0 | 764 | 0.0 | 0.0 | 274.9 | 3.9 | 7.1 |
| 60/15 | 49.62 | 5.8 | −2.67 | 12.0 | 1746 | 0.0 | 108.6 | 1145 | 0 | 18,400 | 0.0 | 1145 | 0.0 | 0.0 | 412.1 | 5.9 | 7.1 |
| 60/30 | 58.62 | 3.6 | −12.62 | 14.7 | 1748 | 0.0 | 108.1 | 1139 | 0 | 18,420 | 0.0 | 1139 | 0.0 | 0.0 | 410.2 | 5.8 | 7.1 |
| 60/60 | 76.62 | 0.4 | −31.77 | >20 | 1747 | 0.0 | 108.6 | 1144 | 0 | 18,410 | 0.0 | 1144 | 0.0 | 0.0 | 412.0 | 5.9 | 7.1 |
| 80/20 | 66.16 | 5.8 | −3.64 | 12.0 | 1710 | 0.071 | 144.7 | 1525 | 37 | 18,020 | 0.7 | 1524 | 95 | 95 | 549.1 | 7.8 | 7.1 |
| 80/40 | 78.16 | 3.6 | −16.58 | 14.6 | 1712 | 0.077 | 144.7 | 1525 | 20 | 18,040 | 0.8 | 1524 | 3.2 | 3.2 | 549.1 | 7.8 | 7.1 |
| 80/80 | 102.2 | 0.4 | −42.42 | >20 | 1712 | 0.074 | 144.5 | 1524 | 10 | 18,040 | 0.8 | 1523 | 0.0 | 0.0 | 548.5 | 7.8 | 7.1 |
| 100/25 | 82.70 | 5.7 | −5.19 | 12.1 | 1675 | 0.734 | 178.8 | 1900 | 310 | 17,650 | 7.7 | 1885 | 7267 | 7267 | 684.2 | 9.7 | 7.1 |
| 100/50 | 97.70 | 3.6 | −20.89 | 14.6 | 1678 | 1.092 | 179.4 | 1906 | 230 | 17,650 | 11.5 | 1890 | 2878 | 2878 | 686.2 | 9.7 | 7.1 |
| 100/100 | 127.7 | 0.4 | −53.09 | >20 | 1675 | 1.344 | 179.5 | 1908 | 142 | 17,650 | 14.2 | 1892 | 246 | 246 | 686.9 | 9.8 | 7.1 |
| Installed Capacity of PV/Battery Capacity (kW/kWh) | Economic Outputs | Technical Outputs | Environmental Outputs and Other Indicators | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| System Price (Thousand €) | IRR (%) | NPV (Thousand €) | Payback (Years) | Cost of Energy Purchased from the Grid (Thousand €) | Benefits from Storage System Usage (Thousand €) | Benefits from Panels Usage (Thousand €) | Solar Generation (Thousand kWh) | Cycles of the Storage System Consumed (Cycles) | Energy Bought from the Grid (Thousand kWh) | Energy Consumed from Storage System (Thousand kWh) | Energy Consumed from Panels (Thousand kWh) | Energy Exported to the Grid (Thousand kWh) | Fed-In Energy Lost (Thousand kWh) | Reduction of Carbon Emissions (Thousand kg) | Degree of Self-Sufficiency (%) | LCOE (cts/kWh) | |
| 80/4 | 56.56 | 8.0 | 6.68 | 9.8 | 1713 | 0.031 | 144.7 | 1526 | 84 | 18,050 | 0.3 | 1525 | 0.490 | 0.499 | 549.2 | 7.8 | 7.1 |
| 80/8 | 58.96 | 7.4 | 4.15 | 10.4 | 1712 | 0.501 | 144.8 | 1527 | 66 | 18,040 | 0.5 | 1526 | 0.320 | 0.320 | 549.7 | 7.8 | 7.1 |
| 80/16 | 63.76 | 6.3 | −0.96 | 11.5 | 1709 | 0.066 | 144.9 | 1528 | 44 | 18,010 | 0.7 | 1527 | 0.121 | 0.121 | 550.0 | 7.8 | 7.1 |
| 80/20 | 66.16 | 5.8 | −3.64 | 12.0 | 1710 | 0.707 | 144.7 | 1525 | 37 | 18,020 | 0.7 | 1524 | 0.095 | 0.095 | 549.1 | 7.8 | 7.1 |
| 80/25 | 69.16 | 5.2 | −6.94 | 12.7 | 1710 | 0.070 | 144.5 | 1524 | 29 | 18,020 | 0.7 | 1523 | 0.048 | 0.048 | 548.6 | 7.8 | 7.1 |
| 80/30 | 72.16 | 4.7 | −9.97 | 13.3 | 1712 | 0.074 | 145.0 | 1529 | 26 | 18,040 | 0.8 | 1528 | 0.014 | 0.014 | 550.4 | 7.8 | 7.1 |
| 80/35 | 75.16 | 4.1 | −13.12 | 13.9 | 1712 | 0.075 | 145.1 | 1530 | 22 | 18,040 | 0.8 | 1529 | 0.010 | 0.010 | 550.7 | 7.8 | 7.1 |
| 80/40 | 78.16 | 3.6 | −16.58 | 14.6 | 1712 | 0.077 | 144.7 | 1525 | 20 | 18,040 | 0.8 | 1524 | 0.003 | 3.210 | 549.1 | 7.8 | 7.1 |
| 100/5 | 70.70 | 7.9 | 7.92 | 9.9 | 1677 | 0.196 | 179.8 | 1911 | 425 | 17,670 | 2.1 | 1895 | 13.39 | 13.39 | 687.8 | 9.7 | 7.1 |
| 100/10 | 73.70 | 7.3 | 4.42 | 10.5 | 1676 | 0.356 | 178.9 | 1900 | 380 | 17,660 | 3.8 | 1885 | 11.27 | 11.27 | 684.2 | 9.7 | 7.1 |
| 100/20 | 79.70 | 6.2 | −1.93 | 11.6 | 1676 | 0.623 | 179.0 | 1902 | 329 | 17,660 | 6.6 | 1886 | 8.238 | 8.238 | 684.7 | 9.7 | 7.1 |
| 100/25 | 82.70 | 5.7 | −5.19 | 12.1 | 1675 | 0.734 | 178.8 | 1900 | 310 | 17,650 | 7.7 | 1885 | 7.267 | 7.267 | 684.2 | 9.7 | 7.1 |
| 100/30 | 85.70 | 5.3 | −7.89 | 12.6 | 1676 | 0.823 | 179.9 | 1911 | 289 | 17,660 | 8.7 | 1895 | 6.067 | 6.067 | 688.0 | 9.7 | 7.1 |
| 100/35 | 88.70 | 4.8 | −11.19 | 13.1 | 1,676 | 0.897 | 179.6 | 1908 | 270 | 17,660 | 9.4 | 1892 | 5.054 | 5.054 | 686.9 | 9.7 | 7.1 |
| 100/40 | 91.70 | 4.4 | −14.40 | 13.6 | 1677 | 0.974 | 179.7 | 1909 | 257 | 17,670 | 10.3 | 1894 | 4.194 | 4.194 | 687.3 | 9.7 | 7.1 |
| 100/50 | 97.70 | 3.6 | −20.89 | 14.6 | 1678 | 1.092 | 179.4 | 1906 | 230 | 17,650 | 11.5 | 1890 | 2.878 | 2.878 | 686.2 | 9.7 | 7.1 |
References
- Yamamoto, Y. Pricing electricity from residential photovoltaic systems: A comparison of feed-in tariffs, net metering, and net purchase and sale. Sol. Energy 2012, 86, 2678–2685. [Google Scholar] [CrossRef]
- Bryans, D.; Amstutz, V.; Girault, H.H.; Berlouis, L.E.A. Characterisation of a 200 kW/400 kWh vanadium redox flow battery. Batteries 2018, 4, 54. [Google Scholar] [CrossRef] [Green Version]
- Kurzweil, P.; Shamonin, M. State-of-charge monitoring by impedance spectroscopy during long-term self-discharge of supercapacitors and Lithium-Ion batteries. Batteries 2018, 4, 35. [Google Scholar] [CrossRef] [Green Version]
- Nastasi, B.; Lo Basso, G. Power-to-Gas integration in the transition towards future urban energy systems. Int. J. Hydrog. Energy 2017, 42, 23933–23951. [Google Scholar] [CrossRef]
- Abdin, G.C.; Noussan, M. Electricity storage compared to net metering in residential PV Applications. J. Clean. Prod. 2018, 176, 175–186. [Google Scholar] [CrossRef]
- Londo, M.; Matton, R.; Usmani, O.; van Klaveren, M.; Tigchelaar, C.; Brunsting, S. Alternatives for current net metering policy for solar PV in the Netherlands: A comparison of impacts on business case and purchasing behaviour of private homeowners, and on governmental costs. Renew. Energy 2020, 147, 903–915. [Google Scholar] [CrossRef]
- Nikolaidis, A.I.; Charalambous, C.A. Hidden financial implications of the net energy metering practice in an isolated power system: Critical review and policy insights. Renew. Sustain. Energy Rev. 2017, 77, 706–717. [Google Scholar] [CrossRef]
- Darghouth, N.R.; Wiser, R.H.; Barbose, G.; Mills, A.D. Net metering and market feedback loops: Exploring the impact of retail rate design on distributed PV deployment. Appl. Energy 2016, 162, 713–722. [Google Scholar] [CrossRef] [Green Version]
- Blank, L.; Gegax, D. Do residential net metering customers pay their fair share of electricity costs? Evidence from New Mexico utilities. Util. Policy 2019, 61. [Google Scholar] [CrossRef]
- Geffert, W.; Strunk, K. Beyond net metering: A model for pricing services provided by and to distributed generation owners. Electron. J. 2017, 30, 36–43. [Google Scholar] [CrossRef]
- Hesse, H.C.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion Battery Storage for the Grid—A Review of Stationary Battery Storage System Design Tailored for Applications in Modern Power Grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef] [Green Version]
- Ayeng’o, S.P.; Schirmer, T.; Kairies, K.-P.; Axelsen, H.; Sauerab, D.U. Comparison of off-grid power supply systems using lead-acid and lithium-ion batteries. Sol. Energy 2018, 162, 140–152. [Google Scholar] [CrossRef]
- Akbari, H.; Browne, M.C.; Ortega, A.; Huang, M.J.; Hewitt, N.J.; Norton, B.; McCormack, S.J. Efficient energy storage technologies for photovoltaic systems. Sol. Energy 2018, 192, 144–168. [Google Scholar] [CrossRef]
- Ru, Y.; Kleissl, J.; Martinez, S. Exact sizing of battery capacity for photovoltaic systems. Eur. J. Control 2014, 20, 24–37. [Google Scholar] [CrossRef]
- Gitizadeh, M.; Fakharzadegan, H. Battery capacity determination with respect to optimized energy dispatch schedule in grid-connected photovoltaic (PV) systems. Energy 2014, 65, 665–674. [Google Scholar] [CrossRef]
- Uddin, K.; Gough, R.; Radcliffe, J.; Marco, J.; Jennings, P. Techno-economic analysis of the viability of residential photovoltaic systems using lithium-ion batteries for energy storage in the United Kingdom. Appl. Energy 2017, 206, 21. [Google Scholar] [CrossRef]
- Yoshida, A.; Sato, T.; Amano, Y.; Ito, K. Impact of electric battery degradation on cost- and energy-saving characteristics of a residential photovoltaic system. Energy Build. 2016, 124, 265–272. [Google Scholar] [CrossRef]
- Cortes, A.; Mazon, K.; Merino, J. Strategy of management of storage systems integrated with photovoltaic systems for mitigating the impact on LV distribution network. Int. J. Electr. Power Energy Syst. 2018, 103, 470–482. [Google Scholar] [CrossRef]
- Azizi, A.; Logerais, P.-O.; Omeiri, A.; Amiar, A.; Charki, A.; Riou, O.; Delaleux, F.; Durastanti, J.-F. Impact of the aging of a photovoltaic module on the performance of a grid connected system. Sol. Energy 2018, 174, 445–454. [Google Scholar] [CrossRef]
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. Photovoltaic energy systems with battery storage for residential areas: An economic analysis. J. Clean. Prod. 2016, 131, 460–474. [Google Scholar] [CrossRef]
- Schram, W.L.; Lampropoulos, I.; van Sark, W. Photovoltaic systems coupled with batteries that are optimally sized for household self-consumption: Assessment of peak shaving potential. Appl. Energy 2018, 223, 69–81. [Google Scholar] [CrossRef]
- Zhang, Y.; Lundblad, A.; Campana, P.E.; Benavente, F.; Yan, J. Battery sizing and rule-based operation of grid-connected photovoltaic-battery system: A case study in Sweden. Energy Convers. Manag. 2017, 133, 249–263. [Google Scholar] [CrossRef]
- Da Silva, G.D.P.; Branco, D. Modelling distributed photovoltaic system with and without battery storage: A case study in Belem, northern Brazil. J. Energy Storage 2018, 17, 11–19. [Google Scholar] [CrossRef]
- Tervo, E.; Agbim, K.; DeAngelis, F.; Hernandez, J.; Kim, H.K.; Odukomaiya, A. An economic analysis of residential photovoltaic systems with lithium ion battery storage in the United States. Renew. Sustain. Energy Rev. 2018, 94, 1057–1066. [Google Scholar] [CrossRef]
- Hanser, P.; Lueken, R.; Gorman, W.; Mashal, J. The Brattle Group. The practicality of distributed PV-battery systems to reduce household grid reliance. Util. Policy 2017, 46, 22–32. [Google Scholar] [CrossRef]
- Talent, O.; Du, H. Optimal sizing and energy scheduling of photovoltaic-battery systems under different tariff structures. Renew. Energy 2018, 129, 513–526. [Google Scholar] [CrossRef]
- European Commision. Photovoltaic Geographical Information System. Available online: https://re.jrc.ec.europa.eu/pvg_tools/en/tools.html#MR (accessed on 18 January 2020).
- Executive Summary—Energy for Competitive Lithuania. Available online: http://enmin.lrv.lt/uploads/enmin/documents/files/National_energy_independence_strategy_2018.pdf (accessed on 12 February 2020).
- Short Version. Available online: http://www.idistributedpv.eu/prosumer-tool/ (accessed on 16 January 2020).
- IRENA. Innovation Landscape Brief: Behind-the-Meter Batteries; International Renewable Energy Agency: Masdar City, Abu Dhabi, 2019. [Google Scholar]
- The Role of Storage in Energy Transition. Available online: https://www.worldenergy.org/assets/downloads/ESM_Final_Report_05-Nov-2019.pdf (accessed on 22 February 2020).













| Battery Capacity for PV Power Plant Size | PV Power Plant Size Pp (kW) | ||||
|---|---|---|---|---|---|
| 20 | 40 | 60 | 80 | 100 | |
| Battery capacity (kWh) | 5 | 10 | 15 | 20 | 25 |
| 10 | 20 | 30 | 40 | 50 | |
| 20 | 40 | 60 | 80 | 100 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aleksiejuk-Gawron, J.; Milčiuvienė, S.; Kiršienė, J.; Doheijo, E.; Garzon, D.; Urbonas, R.; Milčius, D. Net-Metering Compared to Battery-Based Electricity Storage in a Single-Case PV Application Study Considering the Lithuanian Context. Energies 2020, 13, 2286. https://doi.org/10.3390/en13092286
Aleksiejuk-Gawron J, Milčiuvienė S, Kiršienė J, Doheijo E, Garzon D, Urbonas R, Milčius D. Net-Metering Compared to Battery-Based Electricity Storage in a Single-Case PV Application Study Considering the Lithuanian Context. Energies. 2020; 13(9):2286. https://doi.org/10.3390/en13092286
Chicago/Turabian StyleAleksiejuk-Gawron, Joanna, Saulė Milčiuvienė, Julija Kiršienė, Enrique Doheijo, Diego Garzon, Rolandas Urbonas, and Darius Milčius. 2020. "Net-Metering Compared to Battery-Based Electricity Storage in a Single-Case PV Application Study Considering the Lithuanian Context" Energies 13, no. 9: 2286. https://doi.org/10.3390/en13092286
APA StyleAleksiejuk-Gawron, J., Milčiuvienė, S., Kiršienė, J., Doheijo, E., Garzon, D., Urbonas, R., & Milčius, D. (2020). Net-Metering Compared to Battery-Based Electricity Storage in a Single-Case PV Application Study Considering the Lithuanian Context. Energies, 13(9), 2286. https://doi.org/10.3390/en13092286