Design of a Low Torque Ripple Three-Phase SRM for Automotive Shift-by-Wire Actuator
Abstract
:1. Introduction
2. Design of Proposed SRM
2.1. Design Target and Parameters
2.2. Conventional 12/8 SRM
2.3. Non-Uniform Rotor Stucture
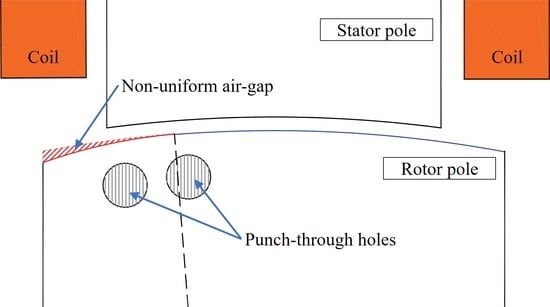
2.4. Proposed Rotor Stucture
3. Simulation Results
3.1. Flux Distribution
3.2. Continuous Torque
4. Experimental Results
5. Discussions
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Smirra, K.; Ferstl, M.; Eiting, T. Mechatronics for “Shift by Wire”—A Technical Challenge; SAE Technical Paper 2007-01–1309; SAE International: Warrendale, PA, USA, 2007. [Google Scholar] [CrossRef]
- Naunheimer, H.; Bertsche, B.; Ryborz, J.; Novak, W. Automotive Transmissions: Fundamentals, Selection, Design and Application, 2nd ed.; Springer-Verlag: Berlin/Heidelberg, Germany, 2011. [Google Scholar] [CrossRef]
- Kobiki, Y.; Inoue, Y.; Sekiguchi, S.; Itoh, T.; Kamio, S. Toyota’s New Shift-by-Wire System for Hybrid Vehicles; SAE Technical Paper 2004-01–1112; SAE International: Warrendale, PA, USA, 2004. [Google Scholar] [CrossRef]
- Nakade, Y.; Kamada, A.; Ueno, K.; Kume, M.; Sakaguchi, K. Shift-by-Wire System for Lexus RWD Vehicles. SAE Int. J. Engines 2017, 10, 689–694. [Google Scholar] [CrossRef]
- Ahn, J.-W.; Lukman, G.F. Switched Reluctance Motor Drives. Modeling Simul. Control Electr. Drives 2019, 275–324. [Google Scholar] [CrossRef]
- Choi, Y.K.; Yoon, H.S.; Koh, C.S. Pole-Shape Optimization of a Switched-Reluctance Motor for Torque Ripple Reduction. IEEE Trans. Magn. 2007, 43, 1797–1800. [Google Scholar] [CrossRef]
- Hieu, P.T.; Lee, D.-H.; Ahn, J.-W. Design of 2-Phase 4/2 SRM for Torque Ripple Reduction. In Proceedings of the 2012 15th International Conference on Electrical Machines and Systems (ICEMS), Sapporo, Japan, 21–24 October 2012; pp. 1–6. [Google Scholar]
- Sheth, N.K.; Rajagopal, K.R. Optimum Pole Arcs for a Switched Reluctance Motor for Higher Torque with Reduced Ripple. IEEE Trans. Magn. 2003, 39, 3214–3216. [Google Scholar] [CrossRef]
- Jing, L.; Cheng, J. Research on Torque Ripple Optimization of Switched Reluctance Motor based on Finite Element Method. Prog. Electromagn. Res. 2018, 74, 115–123. [Google Scholar] [CrossRef] [Green Version]
- Salunke, N.A.; Patel, A.N.; Panchal, T.H. Torque Ripple Reduction of Switched Reluctance Motor by Changing the Rotor Pole Tip Radius. IJRTE 2019, 8, 4256–4259. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, S. Topology Optimization of Rotor Pole in Switched Reluctance Motor for Minimum Torque Ripple. Electr. Power Compon. Syst. 2017, 45, 905–911. [Google Scholar] [CrossRef]
- Nakata, K.; Hiramoto, K.; Sanada, M.; Morimoto, S.; Takeda, Y. Noise Reduction for Switched Reluctance Motor with a Hole. In Proceedings of the Power Conversion Conference-Osaka 2002 (Cat. No.02TH8579), Osaka, Japan, 2–5 April 2002; Volume 3, pp. 971–976. [Google Scholar] [CrossRef]
- Faiz, J.; Tahvilipour, F.; Shahgholian, G. Performance Improvement of a Switched Reluctance Motor. In Proceedings of the 31st Progress in Electromagnetics Research Symposium (PIERS), Kuala Lumpur, Malaysia, 27–30 March 2012; pp. 728–732. [Google Scholar]
- Tekgun, D. Acoustic Noise and Vibration Reduction on Switched Reluctance Machines through Hole Placement in Stator/Rotor Laminations. Master Thesis, The University of Akron, Akron, OH, USA, 2017. [Google Scholar]
- Dickinson, P.G.; Sykes, P.A.; Fulton, N.N.; Durairaj, T.R. Reducing Stress in Electric-Machine Rotors by Optimizing Holes. U.S. 9,246,363, 26 January 2016. [Google Scholar]
- Hashemi, Z.; Zohrabi, F.; Mardaneh, M. A Multi-Objective Optimization of Switched Reluctance Motor Using a Hybrid Analytic-ANFIS Model Considering the Vibrations. Iran. J. Sci. Technol. Trans. Electr. Eng. 2019, 43, 361–371. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S.; Harley, R.G.; Habetler, T.G. Performance Evaluation and Comparison of Multi-Objective Optimization Algorithms for the Analytical Design of Switched Reluctance Machines. CES Trans. Electr. Mach. Syst. 2017, 1, 58–65. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, H.; Zhu, S.; Lu, T. Multi-Physics Multi-Objective Optimal Design of Bearingless Switched Reluctance Motor Based on Finite-Element Method. Energies 2019, 12, 2374. [Google Scholar] [CrossRef] [Green Version]
- Schramm, D.S.; Williams, B.W.; Green, T.C. Torque Ripple Reduction of Switched Reluctance Motors by Phase Current Optimal Profiling. In Proceedings of the PESC ’92 Record. 23rd Annual IEEE Power Electronics Specialists Conference, Toledo, Spain, 29 June–3 July 1992; Volume 2, pp. 857–860. [Google Scholar] [CrossRef]
- Liang, J.; Parsapour, A.; Moallem, M.; Fahimi, B.; Kiani, M. Torque Profile Optimization in Switched Reluctance Motor. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 414–419. [Google Scholar]
- Nakayama, S.; Itoh, T.; Kimura, K. Switched Reluctance Motor. U.S. 7,948,145, 24 May 2011. [Google Scholar]
- Krishnan, R. Switched Reluctance Motor Drives: Modeling, Simulation, Analysis, Design, and Applications; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]















| Parameters | Value |
|---|---|
| Stator outer diameter (mm) | 75 |
| Stack length (mm) | 18 |
| Air-gap length (mm) | 0.25 |
| DC-link voltage (V) | 12 |
| Maximum phase current (A) | 30 |
| Rated speed (RPM) | 1800 |
| Rated torque (Nm) | 0.24 |
| Point | Definition |
|---|---|
| P | Start of overlap between rotor and stator |
| R | Start of “torque overshoot” corner |
| Q | End of “torque overshoot” corner |
| S | End of convexity of torque waveform |
| Design | Phase Current (A) | Torque Ripple (%) |
|---|---|---|
| Conventional | 13.5 | 68.81 |
| Non-uniform | 13.7 | 65.16 |
| Non-uniform, one-hole | 13.8 | 64.27 |
| Proposed | 14.0 | 61.77 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lukman, G.F.; Nguyen, X.S.; Ahn, J.-W. Design of a Low Torque Ripple Three-Phase SRM for Automotive Shift-by-Wire Actuator. Energies 2020, 13, 2329. https://doi.org/10.3390/en13092329
Lukman GF, Nguyen XS, Ahn J-W. Design of a Low Torque Ripple Three-Phase SRM for Automotive Shift-by-Wire Actuator. Energies. 2020; 13(9):2329. https://doi.org/10.3390/en13092329
Chicago/Turabian StyleLukman, Grace Firsta, Xuan Son Nguyen, and Jin-Woo Ahn. 2020. "Design of a Low Torque Ripple Three-Phase SRM for Automotive Shift-by-Wire Actuator" Energies 13, no. 9: 2329. https://doi.org/10.3390/en13092329
APA StyleLukman, G. F., Nguyen, X. S., & Ahn, J.-W. (2020). Design of a Low Torque Ripple Three-Phase SRM for Automotive Shift-by-Wire Actuator. Energies, 13(9), 2329. https://doi.org/10.3390/en13092329