The Impact of Nanofluids on Droplet/Spray Cooling of a Heated Surface: A Critical Review

Abstract

Cooling by impinging droplets has been the subject of several studies for decades and still is, and, in the last few years, the potential heat transfer enhancement obtained thanks to nanofluids’ use has received increased interest. Indeed, the use of high thermal conductivity fluids, such as nanofluids’, is considered today as a possible way to strongly enhance this heat transfer process. This enhancement is related to several physical mechanisms. It is linked to the nanofluids’ rheology, their degree of stabilization, and how the presence of the nanoparticles impact the droplet/substrate dynamics. Although there are several articles on droplet impact dynamics and nanofluid heat transfer enhancement, there is a lack of review studies that couple these two topics. As such, this review aims to provide an analysis of the available literature dedicated to the dynamics between a single nanofluid droplet and a hot substrate, and the consequent enhancement or reduction of heat transfer. Finally, we also conduct a review of the available publications on nanofluids spray cooling. Although using nanofluids in spray cooling may seem a promising option, the few works present in the literature are not yet conclusive, and the mechanism of enhancement needs to be clarified.

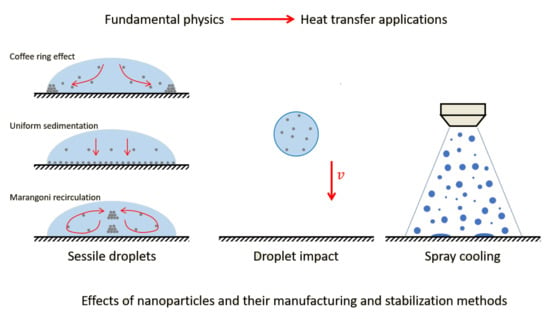
1. Introduction

Considerable research has been conducted on the heat transfer of droplets impinging on a hot substrate [1,2,3]. Despite this attention, heat transfer predictions have remained limited, mainly because of the sophisticated dependence of heat transfer on droplet deformation and spreading over a solid substrate [4,5]. Moreover, the performance of heat transfer using conventional fluids has reached extremes in terms of efficiency. Continuous reduction in size and demand for high-end performance of electronic devices cause a dramatic uptrend in their heat flux generation. Consequently, conventional cooling methods are becoming insufficient in satisfying these cooling needs. In particular, smaller and higher capacity electronics want even more effective cooling, creating a bottleneck for further progress in the microelectronics industry [6,7]. The enhancement of heat removal can be obtained using nanofluids, which possess higher thermal conductivity and have shown, in the last decades, promising results. As an example, several nanofluids, such as Al${}_2$O${}_3$, CuO, and SiC, have been studied extensively using different base fluids and have shown an increased thermal conductivity depending on the nanoparticle size and concentration [8].

The area of drop impact onto solid surfaces is an attractive and extensive subject of experimental, numerical and theoretical studies. Abundant work exists in the literature, which focuses both on the fundamental mechanisms and on the numerous engineering applications [9,10,11,12]. Indeed, in many industrial processes [4,13,14] heat is transferred from a hotter substrate to a droplet, and hence dissipated. This transfer can take place in different ways, such as, by evaporation of sessile droplets, or by bouncing, spreading, and splashing of droplets on a substrate.

When a droplet impacts a substrate, different scenarios are possible depending on the fluid properties, the droplet characteristics (diameter, speed), the impact angle, and surface properties (i.e., hydrophobicity). Figure 1 presents the six most common categorized scenarios: (a) deposition and spreading, (b) prompt splash, (c) corona splash, (d) receding break-up, (e) partial, and (f) complete rebound [4,9,11].

The Weber number, $\mathrm{We}$, together with the Ohnesorge number, $\mathrm{Oh}$, are considered as the most important non-dimensional numbers to develop semi-empirical correlations describing the impact of a droplet on a substrate. These non-dimensional numbers are defined as:

$$\mathrm{Oh}=\frac{\eta }{\sqrt{\rho \sigma d_0}}$$

(1)

$$\mathrm{We}=\frac{\rho d_0{u}_0^2}{\sigma }$$

(2)

where, $\rho$ is the fluid density, $d_0$ is the diameter of the droplet just before the impact, $u_0$ is the droplet impact speed, $\sigma$ is the fluid surface tension and $\eta$ is its dynamic viscosity. The Weber number is a measure of the inertia of the fluid to its surface tension, while the Ohnesorge number relates the viscous forces to inertial and surface tension forces. The Reynolds number Re, which quantifies the droplet impulse [15], can be written as a function of the We and Oh as:

$$\mathrm{Re}=\frac{\rho u_0{d}_0}{\eta }=\frac{\sqrt{\mathrm{We}}}{\mathrm{Oh}}$$

(3)

The so-called spread factor $\beta =d/d_0$ is an important parameter for deposition and spreading of a droplet on a substrate. This factor is defined as the ratio between the instantaneous spreading diameter of the droplet onto the substrate and its diameter just before the impact. The maximum value of the spreading-factor influences the heat transfer rate by limiting the contact area between the droplet and the substrate [16,17,18,19,20]. The maximum spread factor of a droplet is therefore defined as:

$${\beta }_{\max }=\frac{d_{\max }}{d_0}$$

(4)

To quantify the maximum spread factor of a droplet on a substrate, several empirical correlations exist. They use as parameters the Weber number [21,22,23,24], the Reynolds number [25] or both [26,27,28]. According to Moon et al. [29], the maximum contact area between a droplet and a substrate increases with the Weber number, whereas the time required to reach that condition decreases, thus improving the cooling efficiency. However, other parameters may play a role. For instance, the spreading behavior is adversely affected by the hydrophobicity of the surface.

To determine the passage from spreading to splashing, several empirical models exist. In general, a splashing constant $K={\mathrm{We}}^{.5}{\mathrm{Re}}^{.25}$ determines this threshold [2,30,31]. This parameter reads sometimes as $K=\mathrm{We}\sqrt{\mathrm{Re}}$ [32,33]. Further discussion and correlations on splashing conditions can be found in [34,35,36]. Riboux and Gordillo [37] model the splashing threshold velocity as a function of involved fluids’ properties, droplet radius, and the mean free path of the surrounding molecules. This model, which also agrees with the results of Xu et al. [38], is valid for viscosity range from $3\times {10}^{-4}$ to ${10}^{-2}$ Pa·s and surface tension range from 17 to 72 mN/m. The criterion for the transition from spreading to splashing is relevant for the spray/wall interaction modeling, as it largely determines the post-impact droplet mass, momentum, and energy distributions. This impact subsequently affects the characterization of the near-wall mixture formation. The transition from spreading to splashing could be observed via secondary droplets when increasing the Weber number and the surface roughness [39]. In a more general sense, K can be written as [2,34]:

$$K=\mathrm{We}{\mathrm{Re}}^{\alpha }$$

(5)

The sign of $\alpha$ determines the effect of viscosity on splashing. According to Almohammadi and Amirfazli, the working fluid’s viscosity promotes splashing until 5 cSt (i.e., $0.5\times {10}^{-5}$ m${}^2$/s). Whereas, this reverses for higher viscosity values due to the main counterbalancing effects on the lamella such as its thickness and spreading velocity [2].

Finally, cooling via drop impact is also linked to evaporation. Three distinct evaporation stages are defined for a single impinging drop: 1. Initial impact, 2. constant contact area, and 3. constant contact angle [40,41]. Semenov et al. [42] expand this droplet evaporation process to four sequential stages:

1

During the initial stage, the droplet reaches its maximum diameter, which depends on both volume and advancing contact angle. Evaporation is neglected in this stage.

2

In the first stage the droplet radius remains constant due to contact line pinning. Evaporation flattens the droplet profile.

3

In the second stage, the contact line unpins and radius decreases while the contact angle stays constant.

4

Lastly, during the final stage, both the contact angle and droplet radius decrease until the droplet completely disappears.

Motivation of the Review

Thanks to their larger thermal conductivity compared to the base liquids [43,44], nanofluids appear to be a very promising way to enhance the heat transfer. The higher thermal conductivity of the nanoparticles mixed to the bulk liquid and their arrangement into percolation pathways can enhance the heat transfer from the substrate to the fluid [45]. In addition to the heat transfer, the droplet behavior is also influenced by the nature of the fluid. Other parameters such as turbulence and change of surface roughness due to nanoparticles are also critical in spray cooling applications. Particles affect the response to deformation as well as the drying and evaporation [46].

In this framework, the present study aims to review the most recent studies addressing the topics of nanofluid drop impact, heat transfer and sessile droplet evaporation on solid substrates. This review article is divided in five sections, including this introduction. In Section 2, we describe the nanofluid synthesis methods and their stabilization mechanisms, and the consequent impact on the nanofluid rheological properties. Nanofluid droplet/substrate dynamics and evaporation of sessile droplets are examined in Section 3. In Section 4, we focus on one specific application by reviewing the literature focused on heat transfer enhancement by nanofluids in spray cooling. We finally end this review in Section 5 with conclusions, which briefly summarizes the main outcomes and the more recent trends of the addressed research topic.

2. Nanofluid Synthesis and Properties

Initial studies on the effects of added particles in heat transfer fluids are performed on suspensions composed of millimeter or micrometer sized particles. Even though some heat transfer enhancement is observed, micron-sized particles in liquids lead to severe problems such as channel clogging, large pressure drops, and erosion of pipelines [47]. Furthermore, agglomeration and settling of particles pose a severe maintenance problem. Later, the concept of nanofluid is rigorously defined and described as a new class of engineered fluid composed of a colloidal mixture of a base liquid with nanometer-sized solid particles with at least one dimension less than 100 nm [48,49]. Recent studies with these particles have shown heat transfer augmentation without any substantial increase in pumping power requirements and other practical problems. In addition, nanofluids are claimed to have good rheological properties, better stability and higher thermal conductivity than their base fluids [50]. Despite the conflicting outcomes, nanofluids represent potential for diverse types of boiling [51]. The change of heat transfer characteristics may be attributed to the deposition of nanoparticles on the heated surface during nucleate boiling, which modifies the surface properties including the wettability and the capillarity [52,53,54].

To calculate the amount of nanoparticles to add into the base fluid, either weight or volume percentages are used. The weight fraction is calculated by dividing the mass of the nanoparticles by the total fluid mass. For the conversion between weight and volume fractions, Equation (6) is applicable [50].

$$\varphi =\frac{\omega {\rho }_m}{\left(1-\omega \right){\rho }_p+\omega {\rho }_m}$$

(6)

where ${\rho }_p$ is the density of the solid material, ${\rho }_m$ is the bulk medium density, $\varphi$ is the volume fraction and $\omega$ is the weight fraction.

The presence of nanoparticles in the bulk has an impact on the nanofluid properties, such as its thermal conductivity, density, and heat capacity. The effective thermal conductivity $k_{\mathrm{nf}}$ of a nanofluid is often modeled as a function of the thermal conductivity of nanoparticles $k_p$ and base fluid $k_m$ as well as the particle concentration. The first model originates from Maxwell [55], which considers a very dilute suspension of spherical particles and ignores any interaction between particles:

$$k_{\mathrm{nf}}{k}_m\frac{k_p+2k_m+2\varphi (k_p-k_m)}{k_p+2k_m-\varphi (k_p-k_m)}$$

(7)

This formulation has been further extended to include the impact of particle shape, the presence of particles of different size as well as the impact of high volume concentration [56,57,58,59]. One of the extended versions of the Maxwell model for spherical (n = 3) and cylindrical (n = 6) particles is given by Hamilton–Crosser [60].

$$\frac{k_{\mathrm{nf}}}{k_m}=\frac{\frac{k_p}{k_m}+(n-1)-(n-1)(1-\frac{k_p}{k_m})\varphi }{\frac{k_p}{k_m}+(n-1)+(1-\frac{k_p}{k_m})\varphi }$$

(8)

Another recently extended Maxwell model for the thermal conductivity including the particle size R and non-local effects in the form of a non-locality parameter h is given by Shaker et al. [59].

$$\frac{k_{\mathrm{nf}}}{k_m}=\frac{1+2\mathfrak{f}\varphi {\mathfrak{h}}^{-3}}{1-\mathfrak{f}\varphi {\mathfrak{h}}^{-3}}$$

(9)

where $\mathfrak{h}=R/h$ and $\mathfrak{f}=\frac{k_p-k_m}{3({\mathfrak{C}}_1{k}_p-{\mathfrak{C}}_2{k}_m)}$ with ${\mathfrak{C}}_1$ and ${\mathfrak{C}}_2$ being constants depending on R and h.

Similarly, the nanofluid density ${\rho }_{nf}$ and heat capacity $C_{p_{nf}}$ are given as [50,61,62,63,64]:

$${\rho }_{\mathrm{nf}}=\varphi {\rho }_p+\left(1-\varphi \right){\rho }_m$$

(10)

$$C_{p_{\mathrm{nf}}}=\frac{\varphi \left({\rho }_p{C}_{p_p}\right)+\left(1-\varphi \right)\left({\rho }_m{C}_{p_m}\right)}{{\rho }_{\mathrm{nf}}}$$

(11)

where $C_{p_m}$ and $C_{p_p}$ are the constant medium and the nanoparticle heat capacities, respectively.

The dynamic viscosity of a nanofluid having a low volume fraction of particles can be predicted by the Einstein formula [65]:

$${\eta }_r=1+2.5\varphi$$

(12)

where ${\eta }_r={\eta }_{nf}/{\eta }_m$, defined as the ratio between the viscosity of the nanofluid ${\eta }_{nf}$ and the bulk ${\eta }_m$, is called relative viscosity. The Einstein formula only works in the dilute regime $(\varphi <0.05)$, where the distortion of the flow field by the rigid spherical particles is the only extra contribution to the viscosity. The Batchelor–Green equation includes another term to take pairwise interactions between particles into account [66,67]:

$${\eta }_r=1+2.5\varphi +C_2{\varphi }^2$$

(13)

The second order term $C_2{\varphi }^2$ varies based on the type of flow and motion of the particles. For Brownian particles in shear flow, $C_2=6.2$. The Batchelor–Green equation is typically valid for $\varphi <0.1$. Although Equation (13) successfully approximates the viscosity of Newtonian fluids, it underestimates the viscosity of a nanofluid with aggregates [68]. The aggregates increase the effective volume fraction, usually beyond 10%. Therefore, Krieger–Dougherty produced a model for more concentrated colloids [68,69,70]:

$${\eta }_r={\left(1-\frac{\varphi }{{\varphi }_{\max }}\right)}^{\left(-2.5{\varphi }_{\max }\right)}$$

(14)

where ${\varphi }_{\max }$ is the maximum particle loading at which the viscosity becomes infinite (no motion without dilation). Selvakumar et al. [71], modified this model, replacing $\varphi$ by the effective volume fraction of clusters ${\varphi }_{\mathrm{eff}}$ to consider the effects of particle clustering and interfacial layer formation based on particle size distribution.

$${\eta }_r={\left(1-\frac{{\varphi }_{\mathrm{eff}}}{{\varphi }_{\max }}\right)}^{\left(C_{\eta }{\varphi }_{\max }\right)}$$

(15)

In this equation, the intrinsic viscosity $\left[\eta \right]=2.5$ is replaced by a fitting constant $C_{\eta }$ to account for the effect of the particle interactions. The particles do not just affect nanofluid viscosity, but they can adsorb onto the air–liquid interface.

For comparisons using the Weber number, the effective surface tension of the nanofluid should also be measured as they generally tend to exhibit substantially smaller surface tension than their base fluids. Murshed et al. [72], observed a significant decrease in the surface tension of nanofluids with 15 nm TiO${}_2$ nanoparticles in water. On the other hand, according to the results of Tanvir et al. [73] that are determined with the adaptation of the pendant drop method, the surface tension of Al${}_2$O${}_3$ in water nanofluid can be assumed as the same as water and constant until a weight concentration of 4%. However, the addition of more particles will increase the surface tension since the distance between particles is shortened. The effect of the nanoparticles on the surface tension and the conflicting results between Murshed and Tanvir are caused by the myriad of interparticle potentials exhibited in nanofluid. The surface tension tends to be reduced when the repulsion between particles is large and surface coverage is small [74]. Any addition of dispersant or surfactant also changes the surface tension through their own adsorption onto the interface as well as by modifying the particle interactions [75]. Thus, we should examine nanofluid synthesis and stabilization to understand those influences.

2.1. Synthesis of Nanofluids

Although nanofluids are simply nanoparticles dispersed into a base fluid, the preparation of stable nanoparticle dispersions is not a simple task. Several problems may occur during the synthesis of nanofluids due to the physical properties of both the nanoparticles and base fluids. Due to their large surface area to volume ratio, nanoparticles form aggregates when directly dispersed into a base fluid. The small size of nanoparticles reduces the gravitational force of particles, reducing any sedimentation or creaming to a degree where the Brownian motion dominates the quiescent dynamics. This Brownian motion causes collisions between particles, requiring extra stabilization measures to overcome the particle aggregation. The choice of nanofluid synthesis protocols is thus vital to obtain the targeted flow and thermal behavior.

Synthesis protocols of nanofluids can be grouped into either one-step or two-step methods, each with their own merits and drawbacks. The one-step method is capable of generating well-dispersed nanofluids with low volume fractions in carefully chosen nanoparticle and base fluid combinations. Upscaling of the production via this type of method is usually limited due to the relatively expensive unit production cost and Brownian motion-induced aggregation at higher volume fractions. One benefit of the one-step method is the rather straightforward prediction of droplet behavior due to the simple composition. On the other hand, the two-step method has nearly no limitation on the choice of nanoparticle and base fluid or the final volume fraction. The unit cost is lowered by using nanoparticles from external suppliers, where inexpensive methods, such as grinding, are used. This gives more freedom in the combination of nanoparticle and base fluid. However, extra deagglomeration steps and stabilization measures are required when using this type of method since the stability of final nanofluids greatly depends on these two factors. Due to these extra measures, the prediction of droplet behavior in two step-methods is rather complicated compared to nanofluids prepared via one-step methods.

2.1.1. One-Step Method

In one-step methods, the nanoparticles are directly synthesized or created in the target base fluid. Nanofluids produced via this method usually present relatively good stability, even without additional stabilization measures, as the result of good monodispersity of nanoparticles achieved therein. It is possible to have direct control over the size range or distribution by simply altering the setup parameters. Since nanoparticles are directly formed in the base fluid, these methods tend to exhibit fewer problems distributing the nanoparticles in the base fluid compared to two-step methods.

The one-step method was one of the earliest ways to produce nanofluids. In 1998, Choi et al. [76] patented their method to prepare nanofluids, which produced and dispersed nanocrystalline particles in the fluid via heating the substance to be dispersed in a vacuum while passing a thin film of the fluid near the heated substance. Later, Chang et al. reported a way of creating TiO${}_2$ nanoparticles in dielectric liquid with precise control on particle size by combining a vacuum arc spray system with an ultrasonic vibrator and rotating electrode [77].

Nanoparticles can also be synthesized directly in the base fluid if it happens to match with the medium. Chakraborty et al. [78] synthesize Cu-Zn-Al layered double hydroxide nanofluids via a co-precipitation technique, using the corresponding nitrate salts and sodium hydroxide solution as precipitating agents. Although it is a concise method of preparing nanofluids, this co-precipitation technique is only applicable to very limited types of nanoparticles. By taking advantage of the solubility products of different ions, this method is limited to precursor salts that are soluble in the base fluid. This limitation makes an extension of this method to other nanofluids very difficult. The preparation methods are not limited to precipitation. High temperature decomposition in an oven or microwave as well as electrochemical synthesis has also been used more to produce nanofluids [79,80].

The one-step method can also be used when the physical properties of the raw materials happen to be a good match. By taking advantage of the low melting point of the raw material, Wang et al. [81] provide a method to synthesize Field’s alloy—PAO oil nanofluids using excess ethyl carbamate as surfactant via nanoemulsion. Their result shows that the product is thermally stable even above the melting point of their raw material.

Continuous synthesis of nanofluids is also possible with the help of a microfluidic microreactor. Wei et al. [82] proposed a concise method to produce Cu nanofluids continuously using a simple reduction reaction between CuSO${}_4$ and N${}_2$H${}_4$. Their end product remains stable with no visible separation for more than 100 h and reasonable control of the particle size was achieved by adjusting the concentration of reactants and their flow rates. This method is potentially applicable for any nanoparticles that can be produced via a simple one-step chemical reaction with by-products that are able to be easily separated. The main limitation of this method is its production rate. Wei et al. used flow rates up to 50 $\mathsf{\mu }$L per minute for each reactant, which suggested that it would take at least 10 min to produce each milliliter of product nanofluid. The production rate can be improved by having multiple microreactors in parallel, however, it is still somewhat problematic to even produce a liter of target nanofluid according to the setup of Wei et al.

Despite being very promising production-wise, not all combinations of nanoparticles and base fluids are suitable for one-step approaches. High unit production cost for methods like a vacuum arc spray system, due to the high current intensity and cooling system used, makes the unit price not very preferable for massive production. Further, the amount of nanoparticles produced via the one-step method is usually fairly limited, making it hard to achieve a higher weight percentage. Chemical synthesis methods, like these used by Chakraborty et al. [83] usually also have the problem where additional ions remaining in the base fluid can introduce additional stabilization problems.

2.1.2. Two-Step Method

The two-step method, which consists of dispersing preferred nanoparticles into the base fluid of choice, is the more widely used preparation method for nanofluids. When nanoparticles from external sources are used, there is no limitation on the combined materials or weight percentages of the final nanofluids. The two-step method is also usually cheaper as nanoparticles used are usually mass-produced at the industrial level. Common examples are Al${}_2$O${}_3$ in water, EG, pump oil [84], SiC in EG [85], CuO in water [86,87].

Due to their high specific surface area and surface activity, one of the significant challenges in preparing nanofluids via the two-step method is obtaining nanoparticles that are well dispersed in the base fluid. The step of dispersion can be further divided into three parts: wetting of nanoparticles, deagglomeration of the nanoparticle agglomerates, and stabilizing the dispersed nanoparticles in the base fluid.

The wetting of nanoparticles is to replace the adsorbed molecules on the surface of nanoparticles with base fluid. Most of the time, the nanoparticles used in the two-step method are supplied as dry powder. Hence, the wettability of the nanoparticles with its base fluid is an essential parameter to be considered when choosing the pair. The dispersion of a hydrophobic particle in water or oleophobic particle in oil can be extremely difficult depending on the contact angles or surface energies. The Young–Dupré equation (Equation (16)) is a good indication on the wettability of the surface by comparing the surface tension between the solid and gas phases, ${\gamma }_{SG}$, and the sum of the surface tension between the solid and liquid phases, ${\gamma }_{SL}$, and the surface tension between the liquid and gas phase, ${\gamma }_{LG}$. The spreading parameter, S, indicates that the liquid wets the surface completely when it is larger than zero. Powell et al. [88] conclude that this equation also applies to wetting of ideal nanoscale interfaces when fluid–fluid interfacial tensions are large and the three-phase line between particle, liquid, and air has a small curvature by both studying the behavior of passivated gold nanoparticle at a water interface and molecular dynamics simulations. Mi et al. [89] further confirm that line tension has a large influence on wetting properties for small nanoparticles.

$$S={\gamma }_{SG}-({\gamma }_{SL}+{\gamma }_{LG})$$

(16)

However, the nanoparticles’ anisotropic nature or the capillary force induced by the moisture in the air, may cause nanoparticles to form a cluster before being wetted by the base fluid. This cluster is usually large enough so that its surface can be treated as a rough surface with a particular wetting state. Cassie–Baxter wetting with the trapped air greatly increases the apparent contact angle. Zhang [90], demonstrates that it is possible to change the wetting properties by adsorbing alumina nanoparticles on an aluminum surface via boiling alumina-water nanofluids. Deagglomeration of the nanoparticle agglomerates is hence an inevitable step in all two-step methods.

Conventional deagglomeration methods include the use of a magnetic stirrer, ball mill, homogenizer, propeller, and ultrasound [91]. Schroyen et al. [92] compare the dispersion quality index (DQI), defined as the ratio of the primary particle volume fraction to high shear effective volume DQI = $\varphi$ / ${\varphi }_{\mathrm{eff}}$, of silica nanoparticles in a Polydimethylsiloxane (PDMS) nanofluid prepared using a magnetic stirrer, rotor-stator disperser, and ultrasound probe. They concluded that a higher energy input would be directly translated to better dispersion quality for nanoparticles, with the sample prepared with an ultrasound probe having the best dispersion quality among the three. They also show that longer mixing time with high shear mixing would not effectively improve the dispersion quality, and dispersion quality never exceeds the sample prepared using an ultrasound probe.

Ultrasound is the most accepted deagglomeration method, fast and effective due to its high energy intensive nature. The ultrasound technique can break the agglomeration via two simultaneous mechanisms: periodic stretching of particle agglomerates via standing wave and cavitation [93]. It is essential the parameters are optimized when using ultrasound since non-ideal sonication can lead to a few unexpected results. Common unwanted outcomes are boiling of nanofluids due to the energy dissipated and damage to the ultrasonic probe. It is also reported that changes in the particle parameters may occur when sonication is done improperly [94,95]. Taurozzi et al. [96], discuss a number of specific considerations when preparing nanofluids using the two-step method with an ultrasound in their special publication notes for NIST. A comparison of the different parameters on the impact of sonication is summarized by Kaur et al. [97]. A key drawback in sonication is the limited penetration depth of the ultrasonic waves. The attenuation is increased with the particle load, making this method ineffective for dense suspensions.

Ball mill is a common deagglomeration method in preparing nanofluids with a wide range of volume fraction up to 55 vol% [98]. This method is particularly useful when preparing nanofluids with relatively high solid content, as the movement of nanoparticles will be restricted by its neighbor due to the void being occupied. However, ball mills are not usually recommended if an alternative deagglomeration method is applicable for a few reasons: loss of materials due to adsorption of nanoparticles to the balls and container, introduction of foreign particles due to balls being worn down during the milling process, and also possible structural transformations or induced crystal disorder to amorphous materials. Zielinski et al. [99] demonstrated that changes in the morphology of different types of alumina are possible at room temperature using high energy ball milling after just 30 min of milling. There are also other reports of crystal disorder being introduced with ball milling [100], meaning the physical properties of nanoparticles added could be altered. The changes to the particle properties have far-reaching implications, not just on the nanoparticle suspension stability, but also on the heat transfer performance.

2.1.3. Stabilization Mechanisms

Good stability of nanofluids prepared with the two-step method can be achieved with careful control of added stabilization additives. For example, Li et al. [85] maintain no visual separation for 30 days with SiC–Ethylene Glycol nanofluids up to 1.0 vol%, using polyvinylpyrrolidone (PVP) as dispersant and NaOH as pH regulator.

Common stabilization additives in nanofluids can be divided into three groups: inorganic electrolytes, surfactants, and organic polymer dispersants. The three groups of additives are targeting at different stabilization mechanisms of nanofluids. Inorganic acids or bases alter surface charge density (zeta potential) on the particles by changing the pH value of base fluid, while inorganic ions modify the thickness of the diffuse layer. Surfactants form a physical barrier for the nanoparticles by adsorbing on the surface of the particles. When strongly adsorbed onto the surface and extending sufficiently far from the surface, organic polymer dispersants can decrease the effect of van der Waals force through the steric stabilization.

Repulsion effects arising from the same type of charge in the electric double layer outside the particles is the easiest one to be applied. The zeta potential, the electric potential at the slipping plane of particles, has direct relation with the pH value of base fluid [101]. Menon et al. [102] and Das et al. [103] demonstrate that the stability of nanofluids can be simply altered by changing the pH value of the base fluid. Bondarenko et al. [104] use sodium pyrophosphate to increase the repulsion effect in AlSi-water nanofluids. Both the surface charge density and ion concentration determine the effectiveness of these electrostatically stabilized layers.

Surfactants are the most used stabilization additives among the three. By directly adsorbing on the particle surface, ionic surfactants provide additional electrostatic repulsion, while nonionic surfactants can provide extra steric repulsion. The selection of surfactants is based on the type of charge carried on the surface of the nanoparticles after the modification of the pH value, or hydrophilic–lipophilic balance (HLB) of the surfactant if the base fluid is hydrophobic. Common surfactants added are sodium dodecyl sulfate (SDS) for cationic surfactants, cetyl trimethyl ammonium bromide (CTAB) for anionic and oleic acid for nonionic. There are two main issues to be considered when using surfactants: solubility of the surfactant in base fluid and concentration. The solubility of surfactants can typically be deduced from its HLB value. A higher HLB value indicates a more hydrophilic molecule that is more soluble in aqueous environments and vice versa. The critical micellar concentration (CMC) of the surfactant is the concentration where any further addition of surfactant will only form micelles in the environment rather than free surfactant molecules that can be readily adsorbed on surfaces, thus provide a good initial guessing point for tuning. Even when below the CMC, Zhu et al. [105] show that the stability will not always be improved when increasing the surfactant concentration. Their 0.1 wt% Al${}_2$O${}_3$-water nanofluids are stabilized best with 0.1 wt% of sodium dodecylbenzene sulfonate (SDBS) and the stability decrease when increasing the amount of surfactant. They concluded that this is due to the presence of the sodium ion in the surfactant entering the absorbed layer, which reduces the charge density on the particle surface. While both the HLB and CMC can provide guidelines for each surfactant, often the dispersibility must be measured and the concentration tuned for each suspension.

To further improve the stability, organic polymers are sometimes added into nanofluids as a dispersant. Commonly used polymers are polyvinylpyrrolidone (PVP) and polyacrylic acid (PAA) with molecular weight up to 50 kDa. However, the addition of polymers needs more care than the previous two types of additives, since the operation range is usually fairly tight compared to those two. Most organic polymers will have a limit concentration for its dispersion behavior, and start to induce flocculation of nanoparticles when exceeding the limit. Das et al. [103] demonstrate that when using the same type of polymer, increasing the molecular weight will decrease the amount of polymer required for flocculation to happen. This effect, which also depends on the solvent quality, is caused by the purely repulsive entropic and switchable osmotic contributions of the steric layers.

Depending on the length of the polymer and the concentration added, one of the three effects is possible: steric hindrance, induced depletion, and bridging between particles. Furusawa et al. [106] study the mechanism of dispersing behavior of charged polymers. These effects do not necessarily require polymers to be charged, but would usually experience a tighter operating range for concentration. Polymer density, which is influenced by the grafting or adsorption type, also influences the stability and hydrodynamic radius of the particles. Figure 2 demonstrates how the effects experienced by the dispersed particles are directly related to the amount of polymers in the dispersion. This can be manifest in different rheological properties [107] as has been demonstrated for several nanofluids [108,109]. Uncharged polymers will make bridging and induced depletion more likely to happen, as it is harder for them to be adsorbed onto the particle surface. When the nanofluids are used as heat transfer fluids, the temperature change at the contact point during the working condition is usually rather drastic. This may cause the adsorbed polymer to flocculate if the upper or lower critical flocculation temperature is reached [110,111].

2.2. Effects of Additional Stabilization Mechanisms on Droplet Dynamics Behavior

It is worth noticing that the stabilization additives mentioned above not only affect the stability behavior of nanofluids but also inevitably affect the droplet dynamics behavior. While surfactants and other stabilizers certainly help stabilize the particles, some can remain in the base fluid and adsorb to the air–liquid interface. Surfactants, as their name suggests, will decrease the surface tension between fluid and air. Surface tension has a direct link with the work of cohesion of liquid. Thus a decrease in surface tension means less work is required to pull the droplet apart [112]. The contact angle between the droplet and the contact surface would decrease as a direct consequence of lower surface tension between the base fluid and contact surface.

Sarkar et al. [113] find that the addition of polymer dispersant could also have an impact on surface tension. The surface tension of water decreases by 30% when adding just 25 ppm of 40 kDa PVP. Increase of critical heat flux is also observed with PVP concentration up to 110 ppm. Maranzano et al. [114] use a computer simulation to calculate rheological behavior of sterically stabilized colloidal dispersions using polymers with different ratios of particle size and length of polymer steric hindrance layer. They conclude that unless the particle is sufficiently small, with the adsorbed polymer being about the same size as the particle, a hard sphere particle model can be assumed to be valid. In a hard sphere model, there is neither attraction nor repulsion between particles, and the rheological response only depends on the solid volume fraction and thermal Peclet number.

With strong repulsion, on the other hand, the dynamic viscosity will increase as volume fraction increases for nanofluids beyond the standard hard sphere model. Li et al. [115] witnessed an increase in the zero shear dynamic viscosity by about 150% between pure base fluid and 1.0 vol% SiC-EG nanofluids. Additional electrolytes are also found to have an impact on viscosity. Otsuka et al. [116] discover that an additional of 0.1 mM Mg${}^{2+}$ ion will increase the shear stress of their 20 vol% alumina slurry by fourfold, and thus experience a higher viscosity.

Using the findings above, we can therefore determine how the Weber number, the Ohnesorge number and the Reynolds number would change after these stabilization measures are applied. Each of these parameters affects the behavior of droplets in spray cooling. Nanofluids composed of a small volume fraction of well stabilized particles will produce a small increase in bulk density, depending on the choice of materials and volume fraction, but a significant drop in surface tension. A larger droplet is usually harder to form due to the reduction of surface tension. Thus, there is a potential drop in the upper limit of droplet size as well; hence, a higher Weber number would be expected. The Ohnesorge number is expected to increase by a fraction, depending on the amount of surfactants added or volume fraction of nanofluids used. The only parameter that noticeably changes in the Reynolds number would be the dynamic viscosity, but it typically only increases within an order of magnitude. Again, a small decrease in droplet size due to a decrease in surface tension is expected, leading to a reduction of the Reynolds number.

With this understanding, we can explore how these additional stabilization measures would affect droplet behavior. Due to lowered surface tension, a droplet is more likely to break after the initial impact with a substrate. Nguyen et al. [117,118], confirm in two of their publications that the presence of insoluble surfactant would not have any impact on droplet evaporation rate, but the drying patterns are strongly related to the surface state of the surfactant. Similar patterns are further confirmed by Osman et al. using anionic surfactants with three different lengths of carbon chains for soluble surfactant [119]. Figure 3 demonstrates three convective mechanisms compete to form deposit. Bhardwaj et al. [120] use both an experimental and numerical modeling approach to explain the influence of the Derjaguin-Landau-Verwey-Overbeek (DLVO) forces on the drying patterns by altering the pH value. Due to their influence on the surface tension, the nanoparticles in a nanofluid are expected to have a similar effect. All empirical relations on the maximum spread factor are related to the three dimensionless numbers. The effect of stabilization additives towards droplet spreading is hence governed by changes on surface tension for each case. The effect of droplets with high 2D surface loading, however, differ greatly from their surfactant cousins due to the surface elasticity.

As for droplet splashing, the parameter K is highly dependent on the viscosity and surface tension of the working fluid. It is thus mainly depending on the choice of the base fluid. Although a higher value for K can be expected due to the expected increase in Weber number. Exceptions of droplets with high surface loading like pickering emulsion would be less likely to splash due to the solid nanoparticles binding to the surface of the interface [121].

3. Nanofluid Droplet Behavior

3.1. Evaporation of Nanofluids Sessile Droplets

Zhong et al. [122] presents a thorough study about the nanofluid droplet drying process and deposition formation with insoluble components. In general, nanoparticles prolong the duration of the pinning phase, slow down the outward flow due to higher viscosity, modify the surface tension, and alter the evaporation rate. The impact on the nanofluid evaporation rate due to the presence of nanoparticles is the first indication of a modification on the heat transfer process.

According to Sefiane et al. [123], the evaporation rate of nanofluid is higher than that of its base fluid except during the pinning phase, which may be the result of higher viscosity. On the other hand, a shorter evaporation time may also be the result of the enhanced wetting of nanofluids with respect to its base fluid [124]. Moreover, the evaporation rate of a sessile water droplet is considered to be proportional to its perimeter since the main evaporation occurs at the triple contact line. Chen et al. [125] notice a significant change in the evaporation rate along the time, which suggests a dependency of the evaporation rate on the nanoparticle concentration. The types of added nanoparticles also control the changes of the evaporation rate. According to Moghiman and Aslani [126], the presence of TiO${}_2$ nanoparticles slows the evaporation whereas clay nanoparticles help increase the evaporation rate of their base fluid.

When studying nanofluids sessile droplets, the very first analogy encountered is the one with the coffee rings—the expected deposition of nanoparticles on the substrate at the droplet triple contact line. The characteristic pattern from a pinned colloidal droplet is attributed to the capillary flow [127]. There is a lower droplet size limit for the successful formation of a coffee ring pattern, which is found to be 10 $\mathsf{\mu }$m for nanoparticles with a diameter of 100 nm [128]. This so-called coffee ring effect sometimes compromises the overall performance of evaporation involving manufacturing processes such as printing, biochemical analysis, and manufacturing of nanostructured materials [129].

Chon et al. [130] studied the impact of water-based nanofluids with different nanoparticle types and sizes on the evaporation rate of a sessile droplet on a heated substrate. Respectively, nanofluid evaporation consists of three periods: The liquid dominant evaporation (I), in which the suspended nanoparticles have minimal effect; the dryout progress (II), where the nanoparticles start to dominate as water diminishes and therefore cause a discontinuous surge of temperature and heat flux due to its relatively higher thermal conductivity; and finally the formation of nanoparticle stains (III), which brings size dependency.

As shown in Figure 4, smaller nanoparticles accumulate more uniform compared to the larger nanoparticles. As a result the temperature span between the center and edges of the droplet increases with increasing particle size. Due to the large difference of thermal conductivity between nanoparticles and water, a thicker ring-shaped edge accumulation of larger nanoparticles results in a larger temperature span.

Moffat et al. [131] observe the so-called “stick-slip” behavior when TiO${}_2$ nanoparticles are added to ethanol, whereas pure ethanol vaporizes with a constant contact angle. The triple contact line remains pinned during the stick period, causing the contact angle to decrease and letting the nanoparticles deposit at the edge. After reaching a threshold, the drop slips and reaches to a more thermodynamically stable position. Askounis et al. [132] further studied the nanoparticle layer’s structure deposited on the substrate using atomic force microscopy (AFM). The AFM is successfully used to identify the dimensions and shape of ring-stain deposits from free evaporating nanofluid droplets on the nanoscale.

From the substrate point of view, hydrophobic surfaces favor the depinning of the contact line. On the contrary, nanoparticles promote the pinning of the contact line on both hydrophobic and hydrophilic surfaces. This effect is due to a higher energy barrier for depinning, which increases with the nanoparticle concentration [133].

Askounis et al. [134], observed this “stick-slip” behavior in a low-pressure chamber using 80 nm mono-dispersed SiO${}_2$ particles in water. During the evaporation, sessile droplets surprisingly form disordered nanoparticle patterns at the edges. A control of the disordered region formation allows the assembly of desired patterns on the surfaces. In their study, Askounis et al. [134] conducted experiments under low pressure conditions to promote flow velocity and control these unexpected patterns for the exploitation in various nanotechnological applications. Further investigations [135] show that these disordered regions also occur during free evaporation under 750 mbar environment pressure. Decreasing the chamber pressure to 500 mbar, and further to 250 mbar, leads to faster evaporation, which results in forming a single uniform ring. Further decrease of the pressure down to 100 mbar causes more irregular shapes because some part of the fluid cannot find the required time-frame to flow before evaporation. Figure 5 demonstrates these patterns. Another study at low pressure conditions, conducted by Orejon et al. [136], demonstrates that small amounts of nanoparticle addition, less than 0.1 wt%, does not modify the evaporation kinetics for pinned contact lines in a measurable way. Indeed, their unifying correlation predicts the constant radius evaporation kinetics under sub-atmospheric pressure levels for both water and Al${}_2$O${}_3$-water nanofluid droplets having this small weight fraction.

Sefiane et al. [124] study the spreading dynamics Al${}_2$O${}_3$-ethanol nanofluid droplet on a Teflon-coated hydrophobic solid surface by expelling or withdrawing the nanofluid at a fixed volumetric flow rate. He observed that the dynamic contact line velocity increases with nanofluid concentrations up to 1 wt% due to the pressure gradient within the nanofluid. On the contrary, the dynamic wetting remains unimpacted even beyond this value, which may be the result of the dominant viscous forces with respect to structural disjoining pressure [137,138].

To simulate the drying process of a nanofluid droplet, Zhang et al. [139] propose a modeling approach based on kinetic Monte Carlo using chemical potential, which is a function of time and droplet radius. This model predicts branched structure formation due to nanoparticle aggregation during the drying of the nanofluid droplet. Moreover, they observed that the velocity of the contact line decreases in time during evaporation. In other words, higher particle concentration slows down the droplet shrinking process. Yet, the average shrinking velocity increases with a shorter initial boundary, smaller chemical potential, and a higher decrease rate of the chemical potential.

Other studies are focused on the behavior of pure droplets placed on a substrate and surrounded by a nanofluid. Wasan et al. [140] show that when a pure oil droplet wets and spreads on a solid substrate and is immersed into nanofluid, the structural disjoining pressure becomes of importance. As the nanofluid diffuses within the wedge film, thus spreading, the pure droplet separates from the surface. An increase in nanoparticle concentration, temperature, and surface hydrophilicity accelerate this detachment [141]. Nanoparticles cause the fluid around the oil particle to form an inner contact line [138]. Inter-facial tension does not significantly depend on the inner contact line velocity if the structural effect dominates. Once a continuously advancing nanofluidic film is formed, the advancing inner contact line movement reaches a constant velocity, independent of the outer contact angle as long as the inter-facial tension is kept constant [142]. On the other hand, higher nanoparticle concentration, smaller nanoparticles, or lower inter-facial tension move the inner contact line more rapidly. The physical phenomenon with a photomicrograph is visualized in Figure 6.

Even for well-dispersed nanofluids, the contact of a droplet with a substrate inevitably induces nanoparticle aggregations with a consequent sinking of the agglomerates downward, near the wall. According to Shin et al. [143], the local aggregation characteristics considerably affect the prediction of effective thermal conductivity and total evaporation time. The increase in nanoparticle volume fraction, causing surface tension drop and enlargement of the initial perimeter, reduce the initial equilibrium contact angle, and the total evaporation time. In other words, higher nanofluid volume fraction results in larger surface/droplet contact areas, thus enhancing heat transfer. Vafaei et al. [144], on the other hand, observed the effect of concentration as well as the average size for Bismuth telluride, Bi${}_2$Te${}_3$, nanoparticles dispersed in water. The addition of a little amount of nanoparticles dramatically changes the contact angle of a sessile droplet on glass or silicon wafer substrates. The measured contact angle indeed first increases with the nanoparticles concentration until it reaches a peak, then starts to decrease. Particle size and mass concentration, have a great effect on contact angle. Increasing nanofluid concentration causes a growth of contact angle up to a peak, then a decrease. Further, the smaller nanoparticles are more influential on the contact angle at the same concentration. Munshi et al. [145] observed the direct relation between the contact angle and nanoparticle size. Within the size interval of 14 and 620 nm, contact angle decreases with the nanoparticle size for the base liquids of water and diethylene glycol. All in all, nanoparticle size and concentration, as well as the substrate, modify the surface tension, thus affecting the force balance at the triple line, contact angle, and surface wettability [146].

3.2. Splashing, Spreading and Heat Transfer Enhancement of Nanofluids

As of today, the thermal conductivity remains the center of attention of the majority of researches related to the heat transfer enhancement by nanofluids. To fully exploit nanofluids potentialities, the understanding on nanofluids impact on other phenomena such as boiling, droplet spreading, and convective heat transfer is essential. However, up to now, only minor efforts are put into this research [147]. As indicated earlier, although dynamics and spreading of boiling and non-boiling nanofluid droplets play a crucial role in many industrial processes such as spray cooling, coating, and ink-jet printing, only a small number of research covers droplet impingement characteristics of nanofluids on solid or liquid surfaces [46]. Figure 7 represents a typical experimental setup to be used for nanofluid droplet dynamics.

The very first attention to nanofluid spreading was given by Wasan and Darsh [137]. On the other hand, Lu et al. numerically studied the dynamic wetting of the water nanodroplets having the diameter ten times of the non-surfactant gold nanoparticles on a gold substrate using molecular dynamics simulations with validated inter-atomic potentials [148]. Nanoparticles also affect other important parameters in droplet dynamics, such as surface tension and wettability [149]. As reported by Chinnam et al. [150], more concentrated nanofluids result in a lower surface tension at the same temperature, whereas it is just opposite according to Bhuiyan et al. [151,152] for different kinds of nanofluids.

Shen et al. [153] conducted research on impinging droplet dynamics, including nanofluids mainly focusing on water droplets impinging on polished and nanoporous structured surfaces at various surface temperatures including two-phase. However, they only compare water and water-based SWCNT nanofluids on polished surfaces at non-boiling surface temperature to determine the nanoparticle effect on spreading dynamics. Their results express that the nanofluids provide more significant spreading rates and diameters and an increase in the early-stage dynamic contact angle [154].

In their studies, Shen et al. [154,155] quantify the heat transfer enhancement based on the droplet evaporation time, which depends on some measured parameters such as droplet impact velocity, transient spreading diameter, and dynamic contact angle. The effects of nanoparticles are discovered by the analysis of water and water-based SWCNT nanofluid droplets impinging on a polished silicon surface. These nanofluids promote larger spreading velocities and diameters with an increase in early-stage dynamic contact angle, thus reducing the total evaporation time up to 20%. On the other hand, the nanostructured surface also enhances the heat transfer for evaporative cooling at lower surface temperatures by 37% compared to the polished one.

Duursma et al. [156] conduct research to see the aluminum nanoparticles’ effect on droplet boil-off, having various base fluids like water, ethanol, and dimethyl sulfoxide. During the experiments, nanofluids drip onto a copper surface, which is cleaned after each test, at a temperature higher than the liquid saturation temperature. Their results claim that the increase in nanoparticle concentration lead to a decrease in the receding droplet breakup on rebound after impingement, in the maximum droplet spreading, and in the maximum recoil height. On the other hand, increasing the surface temperature and Weber number increases the probability of the receding breakup scenario, whereas a higher nanoparticle concentration restrains this breakup.

Murshed et al. [157] perform a study on how hydrodynamic characteristics of droplets are affected by nanoparticle concentration, substrate temperature, and Weber number. Since higher volume fraction stores more considerable kinetic energy, higher nanoparticle concentration enlarges the nanofluid droplet spreading diameter. This phenomenon also applies to high Weber numbers. On the contrary, hotter surfaces cause smaller spreading. As a summary, according to the results, the non-dimensional spreading of nanofluid droplets increases with increased nanoparticle concentration and Weber number, whereas with decreased surface temperature, dispersed nanoparticles significantly influence nanofluids’ spreading characteristics through their properties and Brownian motion of nanoparticles. One should also note that the surface tension of ethylene glycol measures lower than its pure state, which is also the case for water-based nanofluids [72].

Okawa et al. [158] claim that TiO${}_2$-water nanofluid significantly improves the nucleate boiling heat transfer and critical heat flux, even though nanoparticle colloidal dispersion degrades the heat transfer when the surface temperature is too high. In their study, 3.3 mm diameter droplets are released from a 1.2 mm needle via a syringe pump. The heated target substrate is inclined by 40${}^{\circ }$ to avoid secondary droplets, generated by splashing, touching the substrate. The observation of the impact reveals that the droplet spreading area at low plate temperatures is wider for nanofluids. This increase is probably the primary cause of the nucleate boiling heat transfer enhancement. Also note that the effects of nanoparticles in the dispersion within impacting droplets are independent of the Weber number.

Jackson et al. studied the relation between surface wettability and heat transfer enhancement [159]. An inverse heat transfer problem is solved by measuring the droplet temperature at the needle tip and the substrate temperature, using a thermocouple and an IR camera, respectively. Nanofluids result in a significantly higher convective heat transfer coefficient than water during droplet impingement, which increases with surface wettability. In Figure 8, the 0.5 wt.% DWCN nanofluid droplet rapidly reduces the non-dimensional wall temperature, for all three types of substrates, compared to water droplets. Therefore, nanofluids are more effective for droplet impingement cooling than water. Nevertheless, the heat transfer rate does not change for different nanoparticle concentrations.

Contradictory results with TiO${}_2$ particles are reported by Kahani et al. [160] about the effect of surface wettability on heat transfer rate, as shown in Figure 9. Nanofluids’ concentration promotes the cooling efficiency on uncoated and super-hydrophobic surfaces due to its higher thermal conductivity and lower surface tension. In particular, they observed a superior heat transfer enhancement on super-hydrophobic surface compared to water, although no significant change is observed on super-hydrophilic surface. As also can be seen in Figure 10, nanofluid promotes the surface wettability on different substrates.

Another explanation of the heat transfer enhancement observed when using nanofluid is found in their modified thermal and mass transport properties. According to the calculations based on [161], the heat capacity, $C_p$ of the nanofluid decreases by 35% whereas the density, $\rho$, and thermal conductivity, k, increase by only 1% [160]. Consequently, the thermal diffusivity, which measures the ability of a nanofluid droplet to conduct thermal energy with respect to its ability to store thermal energy, also increases. Therefore, the absorbed heat theoretically travels through the droplet faster than it would do in pure water, thus absorbing its full thermal energy faster. This means greater energy absorption by nanofluid for a very short impingement duration because of a quicker distribution throughout the droplet [160]. Thermal conductivity, density and heat capacity of the nanofluid are estimated by Equations (7), (10) and (11) [161].

Magnetic nanofluids are another attractive topic owing to the possibility of controlling some of their properties using magnetic fields. Chien and Weng investigate the effect of both AAO surface morphology effect [162] and magnetic field on the behavior of a sessile droplet [163]. Furthermore, they studied the effect of the substrate morphology on the impact dynamics of AAO droplets using alumina substrates with and without anodic oxidation [164]. As a summary, the AAO structure significantly influences the impact dynamics of a droplet on a solid substrate with a magnetic field. This study may benefit research areas such as smart coating, spray cooling, spray painting, and jet impingement.

These studies are summarized in

Table 1. Summary of the researches outcomes for nanofluid droplet impact.

Reference	Fluid	${\mathit{d}}_0$ [mm]	$\mathit{\sigma }$ [mN/m]	Impingement Conditions	Recording Properties	Surface	Remarks
Shen et al. [153]	Water + ...Au (5 nm) ...Au (10 nm)	1.85 1.27 1.24	72.34 72.36 69.91	$u_0=1.1$ m/s	16,000 fps 9 µm/px	Heated silicon	Nanofluids spread further, having different droplet heights during spreading, and correspondingly different dynamic contact angles.
Shen et al. [154]	SWCNT + Water	1.29	70.52	Re = 1700	7400 fps	Polished silicon	Using a nanofluid or a nanostructured surface can reduce the total evaporation time up to 20% and 37%, respectively, i.e., enhance the heat transfer.
		1.18	72.69	We = 25		Porous silicon Gold-coated polished silicon
Duursma et al. [156]	Al${}_2$O${}_3$ + (20–50 nm) ...Water ...Ethanol ...DMSO			We = 44–183		Insulated copper block	Neither ethanol nor DMSO solutions exhibited much higher heat fluxes or changes in the CHF temperature when they contained various concentrations of nanoparticles. Increasing the nanoparticle concentration discourages this breakup scenario.
Murshed et al. [157]	TiO${}_2$ + EG (15 nm)	1.4	42.3	We = 53–106	500 fps	Aluminum (22–170${}^{\circ }$C)	The higher the concentration of nanoparticles the larger the spreading diameter of nanofluid droplet.
Okawa et al. [158]	TiO${}_2$ + water (21 nm)	3.3		We = 25–239	2000 fps	SS 304 plate	Nucleate boiling heat transfer and critical heat flux are significantly improved due to nanoparticles. However, they degrade the heat transfer at high plate temperatures. Droplet spreading area appears to be wider for the nanofluids at low plate temperatures.
Jackson et al. [159]	DWCN + water (3.5 nm dia., 1–10 $\mathsf{\mu }$m length)		≈ 39		8700 fps (870 fps) IR camera	Monocrystalline silicon wafer (40 ${}^{\circ }$C) uncoated superhydrophobic hydrophilic	Nanofluid droplets significantly enhance convective heat transfer coefficient due to higher thermal conductivity and lower surface tension. Nanoparticle concentration does not affect the heat transfer rate.
Kahani et al. [160]	TiO${}_2$ + water (21 nm)	1.57		${\mathrm{We}}_{\mathrm{water}}\approx 30$ ${\mathrm{We}}_{\mathrm{nf}}\approx 60$	8700 fps (870 fps) IR camera	Silicon wafer uncoated superhydrophobic superhydrophilic	TiO${}_2$ nanoparticles improve the cooling effectiveness of the droplets on uncoated and superhydrophobic surface up to 33% and 214%, respectively.
Chien et al. [164]	Fe${}_3$O${}_4$ + water	≈ 3.4 (0.02 mL)			2000 fps	Anodic Aluminum Oxide (AAO)	An aluminum sheet can be processed to obtain a more hydrophilic surface. AAO structure significantly influences the dynamic impact of a magnetic nanofluid droplet on a solid surface with a magnetic field.
Liu et al. [165]	MWCNT + (Nano-graphite) (Nano-graphene)	2.45	52–55	We = 50–800	10,000 fps	Glass (Hydrophilic) Teflon (Hydrophobic)	Nanoparticles enhance the viscous dissipation during the droplet impact process, thus significantly suppressing the spreading and receding behaviors.
	Epoxy resin

for more compact information. Nevertheless, more studies are encouraged on dynamics of boiling and non-boiling nanofluid droplets impingement as well as spreading and splashing on solid or liquid surfaces as they play a critical role in many engineering processes like spray cooling, coating, and ink-jet printing.

4. Nanofluids Spray Cooling

Spray cooling is a technology used to cool surfaces with very high heat flux densities, and is used during metal production, to cool electronic modules, in light-water reactors following loss-of-coolant accidents, in diode laser arrays, or in cryogenic cooling for human tissues [166,167,168]. The spray cooling technology is based on fundamental heat transfer mechanisms, which are intrinsically linked to the dynamics of droplets on hot substrates. Indeed, sprays with different volumetric fluxes generates droplets, which will differently interact with the heated substrate/wall [169]. Dilute sprays possess a low volumetric flux, Figure 11a, and generate droplets that do not buildup on the substrate, which remains mostly dry. Intermediate sprays, Figure 11b, are characterized by an increased volumetric flux, which leads to interaction between droplets impacting on the hot substrate without the formation of a liquid film. Finally, dense sprays, Figure 11c, have a high volumetric flux and are capable of maintaining a thin liquid film continuously formed on the hot substrate. The droplet dynamics are therefore strongly influenced by the spray volumetric flux. Moreover, the heat transfer between the liquid and the solid can take place in different regimes.

Usually, the spray cooling curve of pure substances contains three distinctive stages according to the temperature of the hot substrate and the coolant properties, a single-phase regime, a two-phase regime, and a critical heat flux regime [173] as given in Figure 12. In the single-phase regime, although the heat dissipation capability is limited compared to the two-phase regime, the system performs high operation stability and uniform distribution of the heat dissipation flux, which is favorable for fragile electronic components and for unstable structures [174]. The use of nanofluids in this regime can substantially increase the cooling performances and enlarge the application to those situations in which the cooling demands a very high amount of heat flux removal from the substrate without reaching extremely high temperatures. In the two-phase flow regime, the liquid flowing on the substrate may boil, thus dramatically increasing the cooling rate until the CHF point.

The way nanofluids affect the spray cooling performances is still insufficiently understood. Recently, spray cooling research was extended to nanofluid applications to enhance heat transfer [170]. Although using nanofluids as a cooling medium seems a promising option for heat transfer enhancement, this is not conclusive, and the mechanism for enhancement needs clarifying. Most studies examine how far nanofluids influence the fluid thermal properties, to both understand and quantify the physical phenomena behind heat transfer enhancement [175,176,177].

As a starting point, Azmi et al. [50] achieve an enhancement of the Nusselt number for the convective heat transfer under turbulent flow conditions going from 29.6% to 38.5%. Liu et al. [87] study boiling heat transfer characteristics of nanofluid jets in the nucleate boiling regime, which lies in a narrow superheat interval of 50–65 K. CuO nanoparticles in water form a sorption layer on the copper surface, thus forming insulation, which decreases surface roughness and contact angle. Consequently, boiling heat transfer significantly drops for nanofluids, whereas the critical heat flux grows by 25%. On the other hand, Mitra et al. [178] experimentally investigated the boiling heat transfer aspects of water-based TiO${}_2$ and MWCNT nanofluids in laminar jet cooling applications. Nanoparticle deposition on a very hot substrate causes an insulation layer, thus keeping CHF within a 5% margin, whereas this deposition shifts the Leidenfrost point to the higher temperatures due to enhanced rewetting. As a result, maximum film boiling of nanofluids occurs at a higher temperature, thus shifting from film boiling to transition boiling sooner. Consequently, an enhancement in the cooling rate is observed. Optical micrographs of the cooled steel plate are represented in Figure 13.

Hsieh et al. [179] investigate spray cooling using different nanofluids containing, among others Ag and MWCNT nanoparticles at various concentrations. They argue that the heat transfer enhancement mechanism is not only caused by an increased thermal conductivity, but also by an intensification of the turbulence level due to viscosity change causing microscale thermal mixing. Another numerical study performed by Lee et al. [180] also supports the importance of turbulence. Dilute nanofluid suspensions are quite effective in heat removal from the surface because the nanoparticles can rebound without sticking to the surface. Higher concentrations may cause more turbulence, causing some particles to leave without any surface contact.

Chakraborty et al. [181,182] study the effect of Cu-Zn-Al and Cu-Al LDH nanofluid, which are synthesized via a one-step co-precipitation technique, in spray cooling for the quenching of a 900 ${}^{\circ }$C metal plate. Not only owing to the thermal conductivity elevation but also the enhanced surface roughness, which is the result of nanoparticle deposition, very similar results are also observed with both nanofluids in similar applications. In [182], increasing thermal conductivity is observed up to 160 ppm, which is 13.9% more than water at its maximum. In fact, at the same nanofluid concentration, even higher spray cooling rate of 18.5% is achieved. As being the optimum, overall heat transfer performance declines after 160 ppm. Additionally, in [181], 15.17% thermal conductivity enhancement is achieved again at 160 ppm whereas 26% achievement is obtained during the spray cooling application. To a further extent, the outcomes of two different surfactant types on Cu-Zn-Al LDH nanofluid are studied from the heat transfer and surface wettability point of view. Although both of the surfactants reduce the surface tension, allowing more contact between the surface and the coolant, the anionic surfactant SDS at 600 ppm shows 20.9% increase in thermal conductivity and improves the cooling rate by 30.7% compared to water, whereas Tween 20 causes a detrimental effect. This comparison is well presented in Figure 14 [78].

Bellerova et al. [183,184] claim an adverse effect on the heat transfer coefficient, due to a 16.45% volume fraction addition of Al${}_2$O${}_3$ nanoparticle to pure water, by a 45% for a jet and a 20% for full cone atomizations. The heat transfer coefficient is calculated solving an inverse heat transfer problem, which uses the surface temperature of the heated plate, measured by a thermocouple. The decrease of the impact duration time and the changes in the thermal properties are the leading causes of this reduction in the heat transfer coefficient. To extend the validity of the empirical correlations reported in previous works, Tseng et al. [185] examined other types of nanofluids, such as TiO${}_2$. A high volume fraction of 14.05% TiO${}_2$ nanoparticles has shown a detrimental effect on the heat transfer coefficient by 35%. According to Chang et al., higher nanoparticle volume fractions cause a decrease in the heat transfer, and the optimum case is obtained with low fraction [186]. In their study, 0.001% volume fraction of Al${}_2$O${}_3$ shows the optimum performance by 14.3% whereas a detrimental effect by 0.3% is seen at 0.05% volume fraction.

A more recent research conducted by Maly et al. [187] addresses the effect of nanofluid synthesis on the rheological properties of the resulting fluid and their consequent impact on the characteristics (size and velocity distribution of droplets, spray cone angle, etc.) of the sprayed nanofluids. Spray characteristics, in general, are dominantly determined by the liquid viscosity and the surface tension, affecting the primary and the secondary breakup processes, respectively. However, in their study, altered thermal properties positively contribute to the cooling performance with marginally deteriorated hydrodynamic spray characteristics due to nanofluids.

As a complementary study at lower mass concentrations of Al${}_2$O${}_3$ nanoparticles, Kang et al. [188] investigate the spray characteristics of nanofluid sprays with the concentration change using a laser measurement instrument. As expected, lower nanoparticle fractions enhance the cooling performance as most of the particles leave the hot surface. Furthermore, droplet diameters and velocities appear to be markedly altered due to the presence of nanoparticles. Therefore, this difference should be considered while comparing the heat transfer enhancement owing to nanofluids.

5. Conclusions

Nanofluids are considered to have a promising heat transfer enhancement potential in cooling applications. They have in principal higher thermal conductivity than their base liquids. However, this potential does not necessarily mean that the cooling efficiency raises just by adding nanoparticles. On the contrary, enhancement or deterioration also depends on the nanofluids’ stabilization mechanisms and rheological properties. Besides the heat transfer, nanoparticles also affect the droplet behavior, thus changing the turbulence level or surface roughness. Note that, even for well-dispersed nanofluids, the contact of a droplet with a substrate inevitably induces nanoparticle aggregations with a consequent sinking.

Nanofluids can be prepared with one-step or two-step methods. With the one-step method, it is possible to produce nanofluids with low volume fraction and good particle monodispersity. At the same time, the production rate and unit operation cost are significant limitations. Nanofluids produced via the two-step method do not have any restriction on the volume fraction or combination between the base fluid and nanoparticles but requires extra dispersion and stabilization measures.

All common stabilization additives will inevitably affect the nanofluid droplet’s physical properties, hence their dynamic and heat transfer behavior. Nanofluids that are stabilized with surfactants will have a lower surface tension resulting in a decrease of the upper limit of the droplet size. Zhu et al. [105] have demonstrated that nanofluids’ thermal conductivity may drop when too much surfactant is added. Behaviors of organic polymer dispersant at different temperatures are also important when polymer-stabilized nanofluids are used as heat transfer fluid.

The coffee ring analogy is the first method to understand the effect of nanoparticles on a fluid evaporating on a substrate. The so-called ‘stick-slip’ behavior may be introduced by the nanofluids changing the constant contact angle evaporation process to pinning–depinning motions [131], and the nanoparticle concentration promotes pinning due to the increase in the energy barrier [133]. Because of the larger thermal conductivity difference between nanoparticles and their corresponding base fluid, a thicker ring-shaped edge accumulation of larger nanoparticles result in a more significant temperature span [130].

Since the evaporation mainly occurs at the triple contact line, enhanced wetting of nanofluids improves the evaporation rate [124]. It is also controlled by the type, size, and concentration of nanoparticles [125]. An increase in nanoparticle concentration causes further surface tension drop and larger surface-droplet contact areas, thus a heat transfer enhancement [143].

Heat transfer enhancement due to droplet impact depends on droplet velocity, transient spreading diameter, and dynamic contact angle. Nanofluids promote larger spreading velocities and diameters with an increase in early-stage dynamic contact angle [154]. Because more kinetic energy can be stored at higher nanoparticle fractions, the droplet spreading enlarges [157]. Larger droplet spreading area is the primary cause of nucleate boiling heat transfer enhancement [158]. Nanofluid concentration supports cooling efficiency due to higher thermal conductivity and lower surface tension [160].

The difference in the spray characteristics due to nanoparticles are also significant when evaluating the improvement of cooling effectiveness. Therefore, the influence of nanofluids as coolants on the atomization mechanism should be further investigated as indicated in [188]. Spray characteristics are dominantly determined by the liquid viscosity and the surface tension [187] and the addition of nanoparticles to the base cooling fluid mainly modify these properties. However, the addition of nanoparticles does not necessarily increase the cooling performance. Some detrimental effects are reported due to high fractions of nanoparticles [183,184,185,186], whereas improved heat transfer is observed with lower values [188]. Dilute nanofluid suspensions are more effective in heat removal from the surface because the nanoparticles can rebound without sticking to the surface. Higher concentrations may cause more turbulence, causing some particles to leave without any surface contact [180] or forming an insulation layer between the substrate and the fluid [87]. The types of surfactants used in the nanofluid stabilization process also have an impact on the heat transfer [78].

In light of these studies, we can conclude that nanofluids demonstrate considerably high potential as a droplet/spray cooling system. Nevertheless, more detailed and broad experimental research should still be conducted to determine both the performances and the operational limits of these fluids when cooling via droplet impact. Moreover, in many of these studies, nanofluids are considered a “black box”, leading to a sort of empiricism that does not provide insights into the observed heat transfer enhancement’s fundamental mechanisms. A more profound coupling between the nanofluids’ rheological behavior and their potentiality in heat transfer enhancement should also be considered. Nanoparticle clustering in nanofluids can have a tremendous impact on heat transfer. The cluster formation is generally modeled using fractal theory [189] and can result in more rapid transport of heat along a preferential direction [190]. However, the cluster formation decreases the contact surface between the nanoparticles and the base fluid and hence a potential decrease in heat transfer. Understanding the impact of particle clustering on heat transfer is essential, as well as the formulation of specific nanofluids that could impede or promote the formation of nanoparticle aggregates. Finally, accurate studies of the droplet and liquid film temperature evolution during the cooling process and in the presence of nanofluids are missing in the literature. These studies are crucial to couple the droplet dynamics, hence the spray physics, to the heat transfer process. Therefore, they should get more attention in the future from the scientific community.