A Hybrid Simulation Model to Predict the Cooling Energy Consumption for Residential Housing in Hong Kong

Abstract

In Hong Kong, buildings consume 90% of the electricity generated and over 60% of the city’s carbon emissions are attributable to generating power for buildings. In 2018, Hong Kong residential sector consumed 41,965 TJ (26%) of total electricity generated, with private housing accounting for 52% and public housing taking in 26%, making them the two major contributors of greenhouse gas emissions. Furthermore, air conditioning was the major source consuming 38% of the electricity generated for the residential building segment. Strategizing building energy efficiency measures to reduce the cooling energy consumption of the residential building sector can thus have far-reaching benefits. This study proposes a hybrid simulation strategy that integrates artificial intelligence techniques with a building energy simulation tool (EnergyPlus™) to predict the annual cooling energy consumption of residential buildings in Hong Kong. The proposed method predicts long-term thermal energy demand (annual cooling energy consumption) based on short-term (hourly) simulated data. The hybrid simulation model can analyze the impacts of building materials, construction solutions, and indoor–outdoor temperature variations on the cooling energy consumed in apartments. The results indicate that using low thermal conductivity building materials for windows and external walls can reduce the annual cooling energy consumption by 8.19%, and decreasing the window-to-wall ratio from 80% to 40% can give annual cooling energy savings of up to 18%. Moreover, significant net annual cooling energy savings of 13.65% can be achieved by changing the indoor set-point temperature from 24 °C to 26 °C. The proposed model will serve as a reference for building energy efficiency practitioners to identify key relationships between building physical characteristics and operational strategies to minimize cooling energy demand at a minimal time in comparison to traditional energy estimation methods.

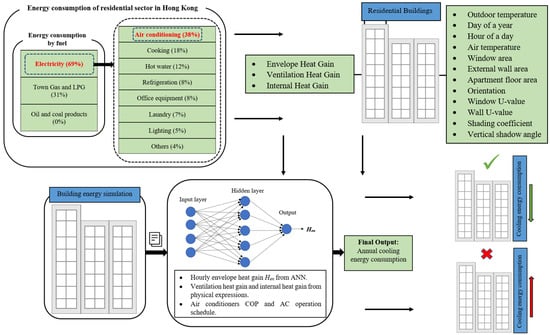
1. Introduction

Climate change is real, and it is happening at a tremendous pace. A substantial increase in greenhouse gas (GHG) emissions across the globe has led to adverse impacts on climate, environment, and human health [1,2]. The construction and building sector is considered to be responsible for 38% of carbon emissions in the world [3]. The final energy consumption associated with buildings was reported to increase from 118 EJ in 2010 to 128 EJ in 2019, and CO₂ emissions related to buildings were 10 Gt in 2019, which were the highest ever recorded. Space cooling was noted to be one of the fastest-growing building energy end uses and its associated energy demand has almost tripled since the 1990′s. It was deemed solely responsible for about 1GtCO₂ emissions and also accounted for 8.5% of total final electricity consumption [4]. Carbon emissions are a direct contributor driving climate change and related events such as global warming, rise in sea level and extreme weather conditions across the globe. For instance, in Hong Kong, the number of very hot days (temperature at 33 °C or above) and hot nights (temperature at 28 °C and above) were found to increase whilst the number of cold days (temperature at 12 °C or below) decreased over the last hundred years [5]. High temperatures and heatwaves associated with extreme heat conditions drove the air conditioning demand which in turn increased electricity requirement worldwide. It is estimated that the energy demand for the buildings are bound to grow by 34% in the coming two decades at an average rate of 1.5% [6]. Moreover, the residential sector is likely to contribute about 67% to energy consumption by 2030 [7]. Residential buildings form a considerable portion of growing energy demand in the world but still, this sector is an undefined energy sink in comparison to other sectors such as industrial, commercial and transport [8]. The energy consumption of other sectors apart from residential has been widely studied and understood due to large economic support and public interest whereas lack of any major incentives was cited for poor initiative towards understanding of energy consumption in residential buildings [9]. These factors emphasize the need to shift focus towards the residential sector for implementing energy saving strategies to have large scale energy conservations and reduce the carbon footprint associated with them.

Hong Kong is one of the most densely populated cities in the world and home to 7.5 million people [10]. While half the world’s population is currently residing in cities, another 2.5 billion people are expected to live in cities by 2050 [11]. The population expansion brings along the requirement to provide affordable and sustainable residential buildings to meet the future needs of the population. To meet the housing needs and to make the high-density environment more liveable for the people in the society, Hong Kong has invested much in the development of high-rise residential buildings. Currently, the housing needs of the Hong Kong residents are mainly met by private housing (53%), public housing (31%), and housing authority subsidized sale flats (15%) [12]. According to its housing statistics, residential flats in private housing increased from 1,258,000 to 1,458,000 whereas flats in public housing grew from 679,000 to 766,000 between 2003 and 2013 [13]. In Hong Kong, buildings consume 90% of the electricity generated and over 60% of the city’s carbon emissions are attributable to generating power for buildings [14]. As per the 2018 energy end-use data of Hong Kong [15], electricity was the major source of energy consumption amounting to 159,493 TJ (55%), and the residential sector accounted for 26% of this total electricity consumption. Moreover, the electricity consumption of the residential sector is more than that of the transport and industrial sector of Hong Kong. The electricity consumption of the residential sector was noted to increase by 13.1% during the period of 2008 to 2018 as well as an average annual growth rate of 1.2% during the same period was recorded [15]. Along with the increase in electricity consumption, an increase in population, as well as household size, was also noted and if adequate energy conservation measures are not taken imminently, electricity consumption figures are expected to rise in the future. In 2018, the total energy consumption of residential buildings in Hong Kong was 60,793 TJ and 69% of this total energy was consumed as electricity, of which 52% was by private housing and 26% by public housing [15]. This is indicative that the private and public housings are the two major constituents of GHG emissions from residential segments of Hong Kong. Additionally, it is also essential to note that Hong Kong being a cooling dominant region, 38% of the electricity consumption was used up for air conditioning of the buildings. The electricity consumption for air-conditioning in the residential sector was also noted to increase by 34% during the period of 2008 to 2018 [15]. Hence, both decarbonizing of the building sector and enhancing cooling energy efficiency of existing buildings as well as new constructions are prime strategies for meeting Hong Kong’s sustainable development goals.

Buildings are one of the major contributors to carbon emissions in the world and switching to a sustainable world requires implementing energy efficiency measures in existing buildings as well as new constructions. As we go through the conception to completion of new buildings and as we perform retrofits to existing buildings to make them more energy-efficient, it is always important to identify key relationships between buildings physical configuration, material properties and operational conditions at a minimal time to provide efficient solutions to reduce the overall cost at a later stage. Cooling energy prediction in residential buildings is often complex and influenced by factors such as construction and building materials, climatic conditions, and occupant behaviors [16]. Three widely used approaches to predict energy consumption within a building are namely, physical models, data-driven approaches, and hybrid methods [17,18]. A physical model utilizes whole building simulation software such as EnergyPlus™ (EP), TRNSYS, etc. to solve numerical equations to predict energy consumption while considering a building’s physical property as well as its associated characteristics. It is also known as the “white box” method as the inner aspects of building physics it works on are quite clear and evident [17]. Moreover, physical simulations through EP do not require historical data of building-related parameters to perform detailed energy analysis. This method, however, is computationally time-consuming and requires expertise to achieve high prediction performance [19]. Additionally, the intricacies associated with the physical method make it infeasible for city-scale energy predictions [20].

With regards to the research and design of residential building energy consumption, there are numerous variables that can influence the overall energy consumption of a building and it is often difficult to handle when these variables are having a non-linear multivariate inter-relationship. To overcome this challenge, it is necessary to have approaches that can efficiently deal with such complex relationships and provide predictions without any significant time lag. To this extent, a data-driven approach, which is an artificial intelligence-based tool can be effectively used to predict the energy consumption associated with buildings. This approach can predict energy consumption without any knowledge of the building physics involved or the building systems associated, and thus is also known as the “black box” method [19]. Some of the well-known data-driven approaches such as support vector machines (SVM), and artificial neural networks (ANN) are capable of providing highly accurate predictions based on input parameters at a reduced computational time [21]. ANN is the most used approach for building energy prediction as shown through previous studies [9,16,17,22,23,24,25,26]. Specifically, ANN is capable to process highly non-linear multivariate inter relationships that exist in building energy analysis and it depends solely on the historical data to provide a prediction of building energy performance [9,25]. Over the last two decades, ANN has found application in building conception, control optimization, energy consumption prediction, retrofit measures and performance evaluations [27]. Kalogirou et al. [28] used back propagation neural networks to predict the heating load of buildings by developing a model using the consumption data of 255 buildings. Aydinalp et al. [29] utilized a neural network to predict the energy consumption associated with equipment, lighting and space cooling for a residential sector. In this work, the superiority of neural networks over physical methods was illustrated. Yezioro et al. [30] compared the performance of the neural network model for the prediction of energy consumption with four simulation tools and found that accurate results can be found through physical modeling but at the expense of very high computational time. The feasibility of conducting of optimisation procedure was also difficult while adopting physical methods for energy estimation. Another study reported similar conclusions stating that the data driven approaches can provide superior simulation speed when compared with its physical method counterparts [31]. The neural network also finds application in indoor temperature control whereby improvement in thermal comfort can be achieved by the prediction of optimal starting time for heating or cooling systems [32]. Accurate prediction of energy consumption is necessary to efficiently manage a building energy network. Mihalakakou et al. [33] developed a neural network methodology based on atmospheric conditions to predict the energy consumption of a dwelling in Greece. The neural network was trained with five years of hourly energy consumption data. The results of the energy consumption of the house on an hourly basis were deemed highly accurate and reliable. However, as dates were not indicated as an input in this study, it was not possible to account for annual changes. Chou and Bui [34] conducted a study using a building’s physical characteristics to predict the heating and cooling load using data-driven approaches. They concluded that ANN and support vector regression (SVR) provided better prediction capabilities compared to other techniques such as classification and regression trees or general linear regression. Ahmad et al. [22] predicted the hourly electricity consumption of an HVAC system using ANN and random forest (RF) and found that the ANN is superior compared to RF. Although, prediction performance of the neural network models relies heavily on the database of input–output relationships, where inadequate data can readily degrade its performance [26].

As discussed earlier, two methods namely, physical and data-driven approaches have their own inherent advantages and disadvantages. Although, the coupling of these two methods presents the possibilities to overcome individual shortcomings. The hybrid approach also known as the grey box model couples the physics in the physical method with statistics of the data-driven approach and thereby eliminates the barriers posed by them when performed individually [35]. It not only possesses a shorter simulation time compared to the physical method but also provides physical interpretation between the input–output database that lacks pure statistical approaches. The creation of hybrid models is a critical and time-consuming process particularly when the input–output dataset is created through several building energy simulations. It may be practical to use physical methods for energy estimation for a single building, although hybrid models provide substantial benefits when it is required to thoroughly exploit the influence of several parameter variations on energy consumption for a broad range of buildings at a minimal time [24]. Once the hybrid model for building energy prediction is developed, the energy prediction can be achieved at a negligible time compared to traditional building performance simulation tools. Moreover, the hybrid tool developed through the coupling of building performance simulation tools and data-driven approaches can work well with non-linear data relationships and also make energy consumption predictions for newer configurations, material specifications and operational conditions without going through the rigorous procedure needed in traditional building performance simulation software. Furthermore, the hybrid model has proved to be more time-efficient and predicts accurately by reducing the computational complexities of traditional physical models [36]. This study proposes a hybrid modeling approach to predict the annual cooling energy consumption for residential buildings in Hong Kong. The proposed model, which can help curb carbon emissions, will be used to lay down desirable building physical characteristics and operational strategies for reducing the cooling energy demand in local apartments.

This paper presents the subject in six sections, including the introduction. Section 2 provides a brief overview of the housing stock in Hong Kong, workflow of the modeling and energy simulation process, integration of the neural network with building performance energy simulation tool and explains the overall methodology adopted to estimate the annual cooling energy consumption of residential buildings. The validity and reliability of the hybrid simulation strategy are shown in Section 3. The application of the proposed model to predict the cooling energy consumption for variation in physical configurations, material properties and operational conditions is discussed in Section 4 and Section 5. Finally, the conclusion, limitations and future direction of the study are summarized in Section 6.

2. Methodology

2.1. Cooling Energy Consumption

Hong Kong is in a subtropical region that necessitates space conditioning. Envelope heat gain, ventilation heat gain and internal heat gain (lighting, occupants and electric equipment) contribute to the amount of heat gained in an indoor environment. The annual cooling energy consumption in an apartment is estimated by,

$$E_c={\displaystyle \sum }_{\mathrm{k}}\frac{{\varnothing }_{AC,k}{(H_{en}+H_{in}+H_{vent})}_k}{CO{P}_k}$$

(1)

where ${\varnothing }_{AC,k}$ is the hourly air conditioner operation schedule in a year for k = 1, 2,…, 8760 h, H_en is the hourly envelope heat gain, H_in is the internal heat gain and H_vent is the ventilation heat gain [37].

H_in is the internal heat gained from lighting and electric equipment, it can be expressed by Equation (2) in terms of floor area A_fl and the sum of equipment power density E_pd and lighting power density L_pd [38].

$$H_{in}=(E_{pd}+L_{pd})\times A_{fl}$$

(2)

The ventilation heat gain H_vent can be expressed as the sum of sensible load L_sen and latent load L_lat,

$$H_{vent}=L_{sen}+L_{lat }; \{\begin{array}{c}{L}_{sen}=N_k\rho V_{vent}{C}_{pa}\left(T_a-T_o\right)\\ L_{lat}=N_k\rho V_{vent}{h}_{fg}\left(w_a-w_o\right)\end{array}$$

(3)

where N_k is the number of occupants at hour k, air density ρ = 1.2 kg m^–3, latent heat of evaporation h_fg = 2436 kJ kg^–1, heat capacity of air C_pa = 1.01 kJ kg^–1 °C^–1, T_a (°C) is indoor temperature, and T_o (°C) is the outdoor temperature. The average ventilation rate V_vent = 3 Ls^–1ps^–1 between the window and split type room air conditioner is used [39]. The indoor moisture content w_a (kg kg^–1, dry air) can be estimated based on the psychrometric chart while the outdoor moisture content w_o (kg kg^–1, dry air) can be estimated using Equation (4), where p_w is the vapor pressure (kPa), p_ws is the saturated vapor pressure (kPa) and R_h,o is the outdoor relative humidity (%),

$$w_o=\frac{p_w}{101.325-p_w}\times 0.622 ; p_w=\frac{R_{h,o}}{100}\times p_{ws}$$

(4)

Air conditioners used in residential buildings are reported to have a maximum coefficient of performance (COP) of 2.9 [40]; their cooling efficiency, which will drop with hourly sensible heat ratio SHR_k, can be calculated by Equation (5) [41].

$$CO{P}_k=\frac{{\left(SH{R}_k+0.45\right)}^{4.9}}{1.1}+0.75$$

(5)

In order to achieve a realistic prediction of cooling energy consumption, occupant behavior should be taken as an essential factor. An occupant load survey of 720 households of government and non-government funded residential buildings in Hong Kong was conducted by Wong and Mui (2006) and using their data, the hourly occupant load N_k can be estimated by Equation (6), where ψ_k is the hourly occupant load variation, N_max is the maximum number of occupants in an apartment, O_a (ps m^–2) is the occupant area ratio and A_fl (m²) is the apartment floor area [42].

$$N_k=N_{max}{\psi }_k; N_{max}=O_a{A}_{fl}$$

(6)

2.2. Prediction of Envelope Heat Gain through a White Box Model

Hong Kong has a high-density living environment with a land population density of about 6700 people/km² [43]. High-rise residential buildings cater to meet the chronic shortage of housing in Hong Kong and also make the highly-dense environment more livable. The private housing sector meets the housing needs of 53% of the households in the city whereas public housing provides shelter to 31% and about 15% of the general public utilize subsidized sale flats under the home ownership scheme [12]. As discussed earlier, the private and public housings sectors are also the two major constituents of GHG emission under the residential building segment. Hence, we considered the public and private housing stock of Hong Kong to analyze different configurations of building physical characteristics and operational strategies that could reduce the carbon emission associated with these buildings in this study. The public housing sector in Hong Kong follows five standard block layouts namely, Concord, Harmony, New cruciform, Slab, and Trident as shown in Figure 1 [44]. The housing layouts in the private sector also closely follow designs adopted by the public housing but more randomness to building design layout is observed. Additionally, while comparing with public housing, provision for having higher apartment floor area, window to wall ratio are often attributed with the design of buildings in the private housing sector of Hong Kong.

To minimize the heat gain from the outdoor environment, an effective envelope design is necessary for residential buildings. Envelope heat gain and fenestration are the two main contributors to the cooling energy demand in buildings [45]. In this study, the range of input parameters listed in

Table 1. Input parameters for envelope heat gain prediction.

Input Parameters	Ranges
Outdoor temperature, To (°C)	Weather data of Hong Kong 1989
Day of a year	1–365
Hour of a day	1–2
Air temperature, Ta (°C)	20–30
Window area, Awd (m2)	2.32–58.179
External wall area, Aen (m2)	5.659–133.63
Apartment floor area, Afl (m2)	12.624–150.04
Orientation (°)	0–360
Window U-value, Uwd (W/(K·m2))	4.2–6.9
Wall U-value, Uwl (W/(K·m2))	0.4–2.9
Shading coefficient, Sc	0.4–0.97
Vertical shadow angle, σv (°)	0.0–89.9

was extracted from design standards, Hong Kong residential property websites, and open literature data [46,47,48,49,50]; the apartment models were created in SketchUp 2019; and the building energy simulation was performed through the OpenStudio^® (OS) cross-platform tool that supports EnergyPlus™ (EP), a superior whole building energy simulation program in terms of user-configurable modular system and variable time step simulation in comparison to its predecessor programs—BLAST and DOE(2) [51]. OpenStudio^® is an EnergyPlus/Radiance framework to easily extend the base capability of EnergyPlus™ for diverse purposes and its abstractions of EP make it more convenient to comprehend new energy models as well as automate a wide array of energy analyses’ [52,53]. It is a strategic component of the United States Department of Energy to leverage the use of advanced building energy modeling specifically EnergyPlus™ for the design and operation of buildings. The base energy model created in OpenStudio^® can be then used for creating design alternatives in the parametric analysis tool (PAT) available within the OpenStudio^® software package. The workflow of the modeling and energy simulation process adopted in this study is illustrated in Figure 2.

The parametric analysis tool provides the capability and flexibility to manually compare numerous design alternatives stemming from various measures/scripts generated within the tool [53]. The measure is a script program written in ruby that provides the functionality to change the insulation properties of walls, modify window to wall ratios, operational settings, occupancy schedules, generate detailed reports of input–output of energy models and so on [54,55]. For instance, by using a measure named Add Remove Or Replace Window Overhangs, a window overhang can easily be generated on a prototype room model as shown in Figure 3. The script file is too long to be listed here but it is easily available from the building component library (BCL) for users, which is an online repository that contains building components and measures [56]. Hence, PAT tool with its diverse functionality was utilized to run EP simulations for different combinations of apartment layouts, operational conditions and material properties.

A total of 620,000 random configurations of physical and operational parameters (i.e., the input parameters in Table 1) were employed. The weather data of Hong Kong in 1989 was obtained from the Hong Kong Observatory for the EP simulations [57]. A database containing the input parameter ranges and their corresponding hourly envelope heat gains generated by the simulations was used to train the ANN model as illustrated in Figure 4.

2.3. Neural Network

The generalization of the neural connection of the human brain into a mathematical model leads to the development of an artificial neural network. The emergence of technological advancements in the last 20 years has paved the way for ANN to find applications in innumerable fields such as aerospace, energy, medical science, etc. [58,59]. The building sector is also not immune to the adoption of artificial neural networks and it is applied to different stages of a building project, including conception, control optimization, energy consumption prediction, retrofitting and performance evaluation [17,27]. While dealing with the energy associated with buildings, it is essential to employ a model that can consider non-linear multivariate interrelationships of parameters in a “noisy environment”. The exponential growth of computing capacity and processing speeds have increased the applicability and reliability of ANN to predict building-related energy performance many folds [58]. Additionally, the capability of ANN to process non-linear input–output relationships with high precision had made it a popular choice over conventional theoretical and empirical methods for building energy efficiency practitioners [16,25]. It is also a very robust system that is noise-immune in nature [36,60]. When building an ANN model for accurate predictions, the choice of neural network architecture and its intrinsic hierarchical characteristics is important. This study proposes a hybrid EP-ANN model to predict the hourly envelope heat gains for private and public residential buildings in Hong Kong. The model uses the backpropagation algorithm (BPA) as a basis. The dataset for training this BPA-based neural network contains abstractions obtained through input–output data from the EP simulations. A conventional three-layer feedforward network which comprises the input layer (12 neurons), the hidden layer (13 neurons) and the output layer (1 neuron) is employed. In addition, the number of neurons in the hidden layer is varied from 12 to 14 with a step increment of one. The Levenberg–Marquardt algorithm (LMA) is used to train the input vectors and their corresponding target vectors. LMA, designed to approach second-order training speed without directly computing the Hessian matrix, outperforms other models such as gradient descent and conjugate gradient methods as shown in previous research studies [61,62]. The Hessian matrix (H_m) is approximated by,

$$Hm=J^{T}J$$

(7)

$$\beta =J^{T}e$$

(8)

where J is the Jacobian matrix, β is the gradient and e is the vector of network errors. The approximation of the Hessian matrix can be obtained by a Newton-like update method,

$$x_{n+1}=x_n-{\left[J^{T}J+\mu I\right]}^{-1}{J}^{T}e$$

(9)

where µ is a scalar known as the Marquardt adjustment parameter. When µ = 0, Equation (9) behaves like Newton’s method using the approximate Hessian matrix; when µ is large, it becomes gradient descent with a small step size.

The trained network can be tested with a set of test data to check the generalized predictability of the neural network. To enhance the generalization ability of the trained neural network, the trainbr function (LMA based Bayesian regularization technique in MATLAB R2020b, MathWorks, Natick, MA, USA) is applied [63,64]. The conventional error function and weight decay components are included in the objective function and Bayes’ rule is used to optimize the regularization parameters in the function. The weights and biases are a Gaussian distribution with random variables. The tan-sigmoid activation function as expressed in Equation (10) is used in the hidden layer and a linear transfer function f_pureline as shown in Equation (12) is applied to the output layer.

$$a_j=f_{tansig}\left(n_j\right)=\frac{2}{1+\exp \left(-2n_j\right)}-1;$$

(10)

$$n_j={\displaystyle \sum }_{j=1}^{10}{\displaystyle \sum }_{i=1}^{12}{P}_{i}I{W}_{j,i}+b_j$$

(11)

where i, j are the numbers of elements in the input vector and hidden layer respectively, a_j is the output from each neuron of the hidden layer, n_j is the net input vector, P_i is the input element of the input layer where i varies from 1 to 12, IW is the input weight matrix where each P_i in the hidden layer is connected to its corresponding neuron, P_iIW_j,i is the weighted input value and b_j is the bias.

$$H_{en}=f_{pureline}\left(n_{out}\right)=n_{out}; n_{out}={\displaystyle \sum }_{j=1}^{10}{a}_{j}L{W}_j+b_{out}$$

(12)

where H_en is the hourly envelope heat gain (W), f_pureline is the linear transfer function, n_out is the net output value, LW_j is the layer weight index and a_jLW_j is the output layer weighted value.

3. Model Validation

The proposed hybrid model was tested with different design and operational configurations for validation. The ANN was trained with one hidden layer and the number of neurons in the hidden layer was varied from 12 to 14. The dataset was split into 70:30 ratios for training and testing the neural network. A big advantage of the LMA based Bayesian regularization technique is that it does not essentially require a validation set, hence more data could be used for training the network [65,66,67]. Figure 5 exhibits the goodness of fit between EP and ANN results for various configurations as listed in

Table 2. Apartment details and other parameters for model validation.

Case	Floor Area (m2)	External Wall Area (m2)	Window Area (m2)	Indoor Set-point Temperature (°C)	Wall U-Value (W/(K·m2))	Window U-Value (W/(K·m2))	Shading Coefficient	Orientation (o)	Vertical Shadow Angle (o)
1	30	22.8	12.3	22	0.5	5	0.9	180	0
2	35.8	31.9	7.6	24	2.9	6.9	0.97	45	75.3
3	65	36.1	15.5	26	1.5	5	0.9	−90	40
4	30	22.8	12.3	24	1.5	5.8	0.7	90	70
5	110	63.8	36.9	22	1.5	4.2	0.9	0	70
6	30.4	30.4	4.2	24	2.9	6.9	0.97	45	75.3
7	145	75.2	40.5	24	1.5	5	0.7	0	70
8	23.9	32.8	5.1	27	2	4.2	0.7	−45	40
9	35.9	40	9.2	24	2.9	6.9	0.97	45	75.3
10	15.1	21.1	4.6	24	2.9	6.9	0.97	45	75.3
11	120	70	35.1	28	0.5	4.2	0.5	180	0
12	135	48.3	63.2	26	0.5	5.8	0.7	0	70
13	52.1	46.4	11.5	26	0.5	5.8	0.5	−90	75.3
14	19.7	17.6	3.7	24	2.9	6.9	0.97	45	75.3

. The selection of a number of hidden neurons was performed through a trial-and-error basis [23,24,58] and it was found that with 13 hidden neurons, the ANN gave a better correlation (R² = 0.947) and a Root Mean Squared Error (RMSE) of 0.0389, indicating a well-trained and well-equipped neural network for predicting envelope heat gains.

The validity of the hybrid simulation strategy used in this study was also tested using the open literature data given by a study performed by Cheung et al. [38] a lighting power density (L_pd) of 18 W/m², an equipment power density (E_pd) of 24 W/m², and an air conditioner operation schedule ϕ_k during the time period from 19:00 to 07:00 on the next day. Figure 6 shows that the prediction results of annual cooling energy consumption produced by the hybrid simulation approach and by Cheung et al.’s [38] study have similar trends. The reason why the former results were higher (approximately 8.5%) may be due to the COP difference. A constant COP of 2.5 was used in Cheung et al.’s [38] study whereas a constant and lower hourly COP_k (as low as 1.5; especially during humid summer nights with a low sensible heat ratio (SHR_k)) was recorded in this study.

4. Results

4.1. Impacts of Building Materials and Construction Solutions on Cooling Energy Consumption

In this study, the insulating properties of walls and windows were derived from various design standards and open access databases [21,30,31,32,33,34]. Figure 7 illustrates the effect of window insulation on the annual cooling energy consumption in an apartment with a floor area of 60 m², a range of window U-values varied from 4.2 to 6.5 W/(K·m²), and a range of shading coefficients varied from 0.4 to 0.8. It is observed that the apartment cooling energy load increases with the window U-value. For instance, with a shading coefficient of 0.6, the annual cooling energy consumption values are 8.8 GJ and 9.19 GJ for window U-values of 4.2 W/(K·m²) and 5.5 W/(K·m²), respectively, giving an increase of 3.4% in the annual cooling energy load. Similarly, with the same window U-value, the cooling energy requirement presents an upward trend following the increase in shading coefficient. Moreover, Figure 7 shows that 8.85 GJ is the lowest annual cooling energy consumption estimated for a U-value of 4.2 W/(K·m²) with a shading coefficient of 0.4, while 9.58 GJ is the highest cooling energy consumption estimated for a U-value of 6.5 W/(K·m²) with a shading coefficient of 0.8. In other words, a reduction of 8.19% in annual cooling energy usage can be achieved when windows combining both a low U-value (e.g., 4.2 W/(K·m²)) and a low shading coefficient (e.g., 0.4) are installed.

The impact of external wall insulation on the annual cooling energy consumed in an apartment was also taken into consideration. Figure 8 exhibits the cooling energy used in apartments when external wall U-values ranged from 0.4 to 2.5 W/(K·m²) and floor areas of 30 m², 60 m² and 90 m². It can be seen in the figure that with a U-value of 2.5, the annual cooling energy usage in the 30 m² apartment is 4.28 GJ while the usage in the 90 m² apartment is 14.42 GJ. According to Figure 8, an average reduction of 7.56% in the annual cooling energy consumption can be reached in all apartments when the U-value is varied from 2.5 W/(K·m²) to 0.4 W/(K·m²).

The window-to-wall ratio (WWR) is an important construction arrangement that creates not only good visual aesthetics but also considerable effects on envelope heat gain in an apartment. Figure 9 depicts the estimation of annual cooling energy consumption for a 60 m²-apartment with WWRs ranging from 20% to 80% (with a step of 20%). The lowest and highest cooling energy consumption values are 7.85 GJ at WWR = 20% and 9.96 GJ at WWR = 80% respectively. The results indicate that increasing the WWR from 20% to 80% increases the annual cooling energy consumption. On the other hand, while maintaining adequate ventilation and visual aesthetics requirements, a reduction of 18% in annual cooling energy consumption can be achieved by decreasing the WWR from 80% to 40%.

4.2. Indoor Temperature Set-Point against Global Warming

Figure 10 illustrates the forecast of annual cooling energy consumption for a 60 m²-apartment using the outdoor temperature T_o variation based on the weather data of Hong Kong in 1989 and a range of indoor set-point temperatures T_in from 23 °C to 26 °C. The variation of outdoor temperature due to global warming was also considered. The highest annual cooling energy consumption (10.35 GJ) and the lowest annual cooling energy consumption (7.63 GJ) can be observed at indoor set-point temperatures of 23 °C and 26 °C respectively. While reductions of 26% and 13.65% in the annual cooling energy consumption can be achieved by changing the indoor set-point temperatures from 23 °C to 26 °C and 24 °C to 26 °C respectively, reductions of 21% and 13.03% can be attained by increasing the indoor set-point temperatures from 23 °C to 24.5 °C and 24 °C to 25.5 °C respectively. In the indoor temperature range 23–25°C, every increment of T_in by 0.5 °C will give a reduction of 7.66% in annual cooling energy consumption; if the indoor temperature is above 25 °C, then every increment of T_in by 0.5 °C will give a reduction of 2.5% in annual cooling energy consumption. Putting global warming into perspective, when the outdoor temperature increases by 1 °C, an increase of 4% in annual cooling energy load from the existing level are estimated for maintaining the indoor set-point temperature at 24 °C, whereas an increase of 6% from the existing level is estimated for maintaining the indoor set-point temperature at 23 °C.

5. Discussions

The heat transfer through the building envelope is primarily an important component that can influence the electricity use related to the cooling of an apartment to maintain thermal comfort for its occupants. It is indicative from this study that the selection of U-value of building material is critical as it can influence the cooling energy consumption of an apartment. It was noted that as the U-value of the external wall increased, a corresponding increase in cooling energy consumption was noted for the different floor areas considered in this study. Needless to say that there exists a linear relationship between cooling energy consumption and the U-value of building material. The cooling energy consumption of the apartment almost doubled as the floor area doubled for the same U-value of the wall. Taking this scenario into consideration it is imperative that if ideal thermal insulations are not provided on the building envelope, the cooling energy consumption of apartments with large floor areas can be very high. On another note, as U-value can be a decisive factor in restricting the amount of heat transferred to the indoor environment, buildings with natural ventilation can avoid thermal discomfort by upgrading the U-value of the building envelope.

The shading coefficient S_c is an index of thermal insulation associated with glazing; the higher the S_c, the lower will be the resistance to heat transfer through solar radiation. The window U-value and S_c play a major role in the increase/decrease in cooling energy consumption as observed in this study. It is to be noted that the choice of tinted or low-emissivity glass with lower S_c values compared to standard clear glass is always preferable for buildings located in the sub-tropical climatic region. At the same time, for a window with a fixed U-value altering the shading coefficient can aid in reducing the cooling energy consumption. In essence, it is essential to interpret from this study that mix and match of U-value and S_c can be achieved based on the need, for instance, if passive solar heating energy is desired, window coupled with high S_c and low U-value can be specified. It is recommended that for buildings located in sub-tropical climatic zones, the usage of windows with lower U-value and lower S_c values can dramatically cut the cooling energy consumption.

To draw further emphasis on the impact of building envelope on the cooling energy consumption, the influence of window-to-wall ratio (WWR) was also examined. The surface area of a window exposed to sunlight can be a very critical parameter in cooling energy consumption. The higher the window surface area exposed to an outside environment with low thermal insulations, the higher will be the cooling energy consumption. A linear relationship between WWR and cooling energy consumption was quite evident from the results of this study. Large luxury flats are often provided with larger WWR compared to public housing in Hong Kong. Large windows can be visually aesthetic but it is also a major contributor for heat gain into the indoor environment. The provision for having large WWR should be provided with appropriate thermal insulations so as minimize the heat gain into the indoor space. At the same time, this study has indicated that reducing the WWR can be an efficient measure to reduce cooling energy consumption. Hence, it is important to strike a balance between visual aesthetics and cooling energy consumption as required.

It was indicated earlier that the number of very hot days and hot nights are increasing whereas the number of cold days is decreasing over the last hundred years in Hong Kong [5]. This trend is almost similar in other parts of the world, where there is a dramatic shift in the average daily temperature been recorded [4]. The increase in outdoor temperature as a result of climate change is driving the cooling energy demand in indoor environments. In order to reduce the cooling energy consumption, it is vital to reduce the indoor set-point temperature. As indicated through this study there are significant energy saving potentials by changing the existing indoor set-point temperatures. Hence, it is urged to the global community to practice setting indoor set-point temperature above existing levels imminently so as to reduce the carbon emissions associated with building cooling energy. The confluence of strategies reported in this study can be a good reference point for building energy efficiency practitioners to improve upon existing knowledge and mitigate the carbon emission associated with the residential sector.

6. Conclusions

The electricity consumption for air conditioning of residential buildings located in sub-tropical climatic regions such as Hong Kong was identified as a major source of GHG emissions through this study. An increase of 13.1% in electricity consumption for the residential sector was recorded for a period between 2008 and 2018. With the increase in population and household size, the residential energy consumption in Hong Kong is expected to rise if adequate measures are not taken to curb the cooling energy demand. Carbon emission from buildings cooling energy consumption is a major constituent causing climate change. Strategizing energy efficiency measures to decarbonize the building sector, especially in high-rise cities such as Hong Kong, can have far-reaching benefits. This study proposed a hybrid simulation strategy that is a testament to the potential of integrating artificial intelligence techniques with a building energy simulation tool (EnergyPlus™) to predict the annual cooling energy consumption for the residential buildings in Hong Kong. The annual cooling energy prediction tool developed will serve as a reference for building energy efficiency practitioners to identify key relationships between building physical characteristics and operational strategies to reduce the cooling energy demand at a minimal time in comparison to traditional energy estimation methods.

The hybrid simulation model of this study can analyze the impacts of building materials, construction solutions, and indoor–outdoor temperature variations on the cooling energy consumed in apartments. The results of this study showed that using low thermal conductivity building materials for windows and external walls can reduce the annual cooling energy consumption by up to 8.19% and decreasing the window-to-wall ratio from 80% to 40% can give annual cooling energy savings of up to 18%. Moreover, significant net annual cooling energy savings of 13.65% can be achieved by changing the indoor set-point temperature from 24 °C to 26 °C. Putting global warming into perspective, however, when the outdoor temperature rises by 1 °C, increases of 4% and 2.5% in annual cooling energy load from the existing levels are estimated for maintaining the indoor set-point temperatures at 24 °C and 25.5 °C, respectively.

To conclude this section a few important insights to this study are drawn to improve the work further. The impact on cooling load due to interaction of buildings such as shading from a neighboring building has not been considered whereas the scenario where the building receives maximum solar heat gain was examined in this study. Shading is noted to reduce the cooling energy demand further in densely packed cooling dominant regions such as Hong Kong, which would be an additional benefit in terms of energy savings rather than a detrimental effect. Although, the addition of this component could improve the effectiveness of the proposed model when it is applied to buildings in different climatic regions. Future studies with respect to the expansion of the proposed methodology of this study to cover different scales of buildings under different climatic conditions shall increase the potentialities of this approach to develop more carbon-neutral buildings in the future. Furthermore, including cost analysis in the proposed methodology will aid stakeholders to implement energy-saving strategies that are cost-effective.