Evaluation of the Effect of Anti-Corrosion Coatings on the Thermal Resistance of Ground Heat Exchangers for Shallow Geothermal Applications
Abstract
:1. Introduction
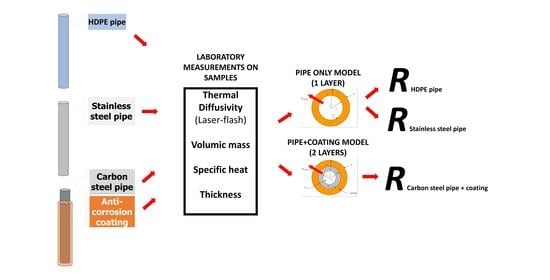
2. Materials and Methods
2.1. Passive and Active Anti-Corrosion Measures for Buried Carbon Steel Pipes
- oxidation products obtained, e.g., by anodic oxidation of metals such as Al, Ni, or Co. The oxides of these materials are very tough and adherent to the surface layer, insulating them from the environment. Metals, such as Zn, could be applied by immersing the Fe-alloy in a galvanic bath of molten Zinc or attaching a bulk sacrificial anode made of Zinc alloy to the pipe in case of stray currents. With Zn being more reducing than Fe, oxidation proceeds on the Zn and the pipe remains protected until all the Zn has been consumed. Moreover, other metals such as Cr, could be applied by plating/cladding the pipes.
2.2. Stainless-Steel Grades with Anti-Corrosive Action Used for Piping
2.3. The LFM Procedure to Measure Thermal Properties

- ec is the effusivity of the coating [J m−2 K−1 s−1/2] ;
- es is the effusivity of the substrate [J m−2 K−1 s−1/2] ;
- ρ is the density [kg m−3];
- λ is the thermal conductivity [W m−1 K−1];
- c is the specific heat capacity [J kg−1 K−1];
- Γ is the function of the effusivity of both coating and substrate ;
- lc is the thickness of the coating [m];
- αc is the thermal diffusivity of the coating [m2 s−1] ;
2.4. Modelling the Thermal Resistance of Each Material and of Different GHE Configurations
- R = the thermal resistance per unit area of the piece of material (m2·K·W−1),
- r1 = represents the inner radius of the pipe (m),
- r2 = represents the outer radius of the pipe (m),
- λ = represents the conductivity of the material (W·m−1·K−1),
- L = represents the length of the pipe, that is assumed to be unitary (m).
- R = the thermal resistance per unit area of the piece of material (m2·K·W−1),
- r1 = represents the inner radius of the pipe (m),
- r2 = represents the outer radius of the inner pipe (m),
- r3 = represents the outer radius of the outer pipe (coating layer) (m),
- λpipe = represents the conductivity of the carbon steel pipe (W·m−1·K−1),
- λcoating = represents the conductivity of the coating material (W·m−1·K−1).
3. Results
3.1. Outcomes of LFM and Thermal Diffusivity Values
3.2. Thermophysical Properties of the Specimens
3.3. Calculation of the Thermal Resistance of Each Material and of Different GHE Configurations
- RHDPE = 9585 × 10−6 [m2·K·W−1],
- RS235JRH = 87 × 10−6 [m2·K·W−1],
- RAISI316 = 273 × 10−6 [m2·K·W−1],
- RAISI304 = 243 × 10−6 [m2·K·W−1].
- Rbitumen = 97 × 10−6 [m2·K·W−1],
- Rtotal = RS235JRH + Rbitumen =184 × 10−6 [m2·K·W−1].
- RPrimer = 32 × 10−6 [m2·K·W−1],
- Rtotal = RS235JRH + RPrimer = 120 × 10−6 [m2·K·W−1].
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Boban, L.; Miše, D.; Herceg, S.; Soldo, V. Application and Design Aspects of Ground Heat Exchangers. Energies 2021, 14, 2134. [Google Scholar] [CrossRef]
- Badenes, B.; Sanner, B.; Mateo Pla, M.Á.; Cuevas, J.M.; Bartoli, F.; Ciardelli, F.; González, R.M.; Ghafar, A.N.; Fontana, P.; Lemus Zuñiga, L.; et al. Development of Advanced Materials Guided by Numerical Simulations to Improve Performance and Cost-Efficiency of Borehole Heat Exchangers (BHEs). Energy 2020, 201, 117628. [Google Scholar] [CrossRef]
- Pockelé, L.; Mezzasalma, G.; Righini, D.; Vercruysse, J.; Cicolini, F.; Cadelano, G.; Galgaro, A.; Dalla Santa, G.; De Carli, M.; Emmi, G.; et al. Innovative Coaxial Heat Exchangers for Shallow Geothermal. In World Geothermal Congress; Elsevier: Reykjavik, Iceland, 2021. [Google Scholar]
- Galgaro, A.; Dalla Santa, G.; Cultrera, M.; Bertermann, D.; Mueller, J.; De Carli, M.; Emmi, G.; Zarrella, A.; Di Tuccio, M.; Pockelé, L.; et al. EU Project “Cheap-GSHPs”: The Geoexchange Field Laboratory. In Energy Procedia; Elsevier: Vienna, Austria, 2017. [Google Scholar] [CrossRef]
- Zarrella, A.; Emmi, G.; Graci, S.; De Carli, M.; Cultrera, M.; Dalla Santa, G.; Galgaro, A.; Bertermann, D.; Müller, J.; Pockelé, L.; et al. Thermal Response Testing Results of Different Types of Borehole Heat Exchangers: An Analysis and Comparison of Interpretation Methods. Energies 2017, 10, 801. [Google Scholar] [CrossRef] [Green Version]
- Quaggiotto, D.; Zarrella, A.; Emmi, G.; De Carli, M.; Pockelé, L.; Vercruysse, J.; Psyk, M.; Righini, D.; Galgaro, A.; Mendrinos, D.; et al. Simulation-Based Comparison between the Thermal Behavior of Coaxial and Double u-Tube Borehole Heat Exchangers. Energies 2019, 12, 2321. [Google Scholar] [CrossRef] [Green Version]
- Mendrinos, D.; Katsantonis, S.; Karytsas, C. Pipe Materials for Borehole Heat Exchangers. In Proceedings of the European Geothermal Congress 2016, Strasbourg, France, 19–23 September 2016; Volume 2016. [Google Scholar]
- Mendrinos, D.; Katsantonis, S.; Karytsas, C. Review of Alternative Pipe Materials for Exploiting Shallow Geothermal Energy. Innov. Corros. Mater. Sci. Former. Recent Pat. Corros. Sci. 2017, 7, 13–29. [Google Scholar] [CrossRef]
- Tang, F.; Nowamooz, H. Factors Influencing the Performance of Shallow Borehole Heat Exchanger. Energy Convers. Manag. 2019, 181, 571–583. [Google Scholar] [CrossRef]
- Zanjani, A.M.; Gharali, K.; Al-Haq, A.; Nathwani, J. Dynamic and Static Investigation of Ground Heat Exchangers Equipped with Internal and External Fins. Appl. Sci. 2020, 10, 8689. [Google Scholar] [CrossRef]
- Paul, K.C.; Pal, A.K.; Ghosh, A.K.; Chakraborty, N.R. Thermal Measurements of Coating Films Used for Surface Insulation and Protection. Surf. Coatings Int. Part B Coatings Trans. 2004, 87, 137–141. [Google Scholar] [CrossRef]
- UNI 9099:1989, Tubi Di Acciaio Impiegati per Tubazioni Interrate o Sommerse. Rivestimento Esterno Di Polietilene Applicato per Estrusione; UNI: Rome, Italy, 1989.
- UNI ISO 5256:1987, Tubi Ed Accessori Di Acciaio Impiegati per Tubazioni Interrate o Immerse. Rivestimento Esterno e Interno a Base Di Bitume o Di Catrame; UNI: Rome, Italy, 1987.
- Cadelano, G.; Bortolin, A.; Ferrarini, G.; Molinas, B.; Giantin, D.; Zonta, P.; Bison, P. Corrosion Detection in Pipelines Using Infrared Thermography: Experiments and Data Processing Methods. J. Nondestruct. Eval. 2016. [Google Scholar] [CrossRef]
- Parker, W.J.; Jenkins, R.J.; Butler, C.P.; Abbott, G.L. Flash Method of Determining Thermal Diffusivity, Heat Capacity, and Thermal Conductivity. J. Appl. Phys. 1961, 32, 1679–1684. [Google Scholar] [CrossRef]
- Akoshima, M.; Baba, T. Thermal Diffusivity Measurements of Candidate Reference Materials by the Laser Flash Method. Int. J. Thermophys. 2005, 26, 151–163. [Google Scholar] [CrossRef]
- Jannot, Y.; Degiovanni, A. Thermal Properties Measurement of Materials; ISTE: London, UK, 2018. [Google Scholar] [CrossRef]
- Ferrarini, G.; Bison, P.; Bortolin, A.; Cadelano, G.; Rossi, S. Thermal Diffusivity Measurement of Ring Specimens by Infrared Thermography. In Thermosense: Thermal Infrared Applications XXXIX; SPIE: Anaheim, CA, USA, 2017. [Google Scholar] [CrossRef]
- Spierings, A.B.; Schneider, M.; Eggenberger, R. Comparison of Density Measurement Techniques for Additive Manufactured Metallic Parts. Rapid Prototyp. J. 2011, 17, 380–386. [Google Scholar] [CrossRef]
- O’Neill, M.J. Measurement of Specific Heat Functions by Differential Scanning Calorimetry. Anal. Chem. 1966, 38, 1331–1336. [Google Scholar] [CrossRef]
- Ferrarini, G.; Bortolin, A.; Cadelano, G.; Finesso, L.; Bison, P. Multiple Shots Averaging in Laser Flash Measurement. Appl. Opt. 2020, 59, E72–E79. [Google Scholar] [CrossRef]
- Bison, P.; Clarelli, F.; Vannozzi, A. Pulsed Thermography for Depth Profiling in Marble Sulfation. Int. J. Thermophys. 2014, 36, 1123–1130. [Google Scholar] [CrossRef]
- Bison, P.G.; Cernuschi, F.; Grinzato, E.; Marinetti, S.; Robba, D. Ageing Evaluation of Thermal Barrier Coatings by Thermal Diffusivity. Infrared Phys. Technol. 2007, 49, 286–291. [Google Scholar] [CrossRef]
- Bison, P.; Cernuschi, F.; Grinzato, E. In-Depth and in-Plane Thermal Diffusivity Measurements of Thermal Barrier Coatings by IR Camera: Evaluation of Ageing. Int. J. Thermophys. 2008, 29, 2149–2161. [Google Scholar] [CrossRef]
- Balageas, D.L.; Krapez, J.C.; Cielo, P. Pulsed Photothermal Modeling of Layered Materials. J. Appl. Phys. 1986, 59, 348–357. [Google Scholar] [CrossRef]
- Luo, Y.; Xu, G.; Yan, T. Performance Evaluation and Optimization Design of Deep Ground Source Heat Pump with Non-Uniform Internal Insulation Based on Analytical Solutions. Energy Build. 2020, 229, 110495. [Google Scholar] [CrossRef]
- Lamarche, L.; Kajl, S.; Beauchamp, B. A Review of Methods to Evaluate Borehole Thermal Resistances in Geothermal Heat-Pump Systems. Geothermics 2010, 39, 187–200. [Google Scholar] [CrossRef]
- De Carli, M.; Tonon, M.; Zarrella, A.; Zecchin, R. A Computational Capacity Resistance Model (CaRM) for Vertical Ground-Coupled Heat Exchangers. Renew. Energy 2010, 35, 1537–1550. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Oxford University Press: Oxford, UK, 1980. [Google Scholar]




| Material | €/ton |
|---|---|
| HDPE | 1080 |
| Mild/low-carbon steel | 900 |
| Stainless steel AISI 304 | 2900 |
| Stainless steel AISI 316 | 3480 |
| Specimen | Thickness [mm] |
|---|---|
| HDPE | 0.570 ± 1% |
| Stainless steel AISI 304 | 1.024 ± 0.5% |
| Stainless steel AISI 316 | 1.100 ± 0.5% |
| Carbon steel S235JRH | 5.486 ± 0.5% |
| Bitumen | 0.657 ± 4% |
| Primer | 0.150 ± 12% |
| Specimen | Estimated Parameter α/l2 [s−1] | Thermal Diffusivity [m2 s−1] |
|---|---|---|
| HDPE | 0.708 ± 0.4% | 0.23 × 10−6 ± 5% |
| Stainless steel AISI 304 | 3.96 ± 0.5% | 4.1 × 10−6 ± 5% |
| Stainless steel AISI 316 | 2.98 ± 0.5% | 3.6 × 10−6 ± 5% |
| Carbon steel S235JRH | 0.422 ± 0.5% | 12.7 × 10−6 ± 5% |
| Bitumen | 0.176 ± 0.4% | 0.08 × 10−6 ± 9% |
| Primer | 11.21 ± 0.5% | 0.25 × 10−6 ± 25% |
| Material | Specific Heat [J·kg−1·K−1] | Density [kg·m−3] | Thermal Conductivity [W·m−1·K−1] |
|---|---|---|---|
| HDPE | 1930 ± 2% | 940 ± 2.5% | 0.41 ± 5% |
| Stainless steel AISI 304 | 500 ± 5% | 7850 ± 2.5% | 16.2 ± 7.5% |
| Stainless steel AISI 316 | 500 ± 5% | 8000 ± 2.5% | 14.4 ± 7.5% |
| Carbon steel S235JRH | 460 ± 5% | 7700 ± 2.5% | 45 ± 7.5% |
| Bitumen | 1720 ± 5% | 1500 ± 2.5% | 0.20 ± 10% |
| Primer | 1100 ± 5% | 2200 ± 2.5% | 0.62 ± 27% |
| Corrosion-Resistant Pipe Configuration | Total Thermal Resistance [m2·K·W−1] | Increased Thermal Resistance Compared to Unprotected Carbon Steel |
|---|---|---|
| 2 mm thickness HDPE | 9585 × 10−6 | ×110 |
| 2 mm thickness stainless steel AISI 304 | 243 × 10−6 | ×2.8 |
| 2 mm thickness stainless steel AISI 316 | 273 × 10−6 | ×3.1 |
| 2 mm thickness Carbon steel S235JRH coated with 0.1 mm of bitumen | 184 × 10−6 | ×2.1 |
| 2 mm thickness carbon steel S235JRH coated with 0.1 mm of primer | 120 × 10−6 | ×1.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cadelano, G.; Bortolin, A.; Ferrarini, G.; Bison, P.; Dalla Santa, G.; Di Sipio, E.; Bernardi, A.; Galgaro, A. Evaluation of the Effect of Anti-Corrosion Coatings on the Thermal Resistance of Ground Heat Exchangers for Shallow Geothermal Applications. Energies 2021, 14, 2586. https://doi.org/10.3390/en14092586
Cadelano G, Bortolin A, Ferrarini G, Bison P, Dalla Santa G, Di Sipio E, Bernardi A, Galgaro A. Evaluation of the Effect of Anti-Corrosion Coatings on the Thermal Resistance of Ground Heat Exchangers for Shallow Geothermal Applications. Energies. 2021; 14(9):2586. https://doi.org/10.3390/en14092586
Chicago/Turabian StyleCadelano, Gianluca, Alessandro Bortolin, Giovanni Ferrarini, Paolo Bison, Giorgia Dalla Santa, Eloisa Di Sipio, Adriana Bernardi, and Antonio Galgaro. 2021. "Evaluation of the Effect of Anti-Corrosion Coatings on the Thermal Resistance of Ground Heat Exchangers for Shallow Geothermal Applications" Energies 14, no. 9: 2586. https://doi.org/10.3390/en14092586
APA StyleCadelano, G., Bortolin, A., Ferrarini, G., Bison, P., Dalla Santa, G., Di Sipio, E., Bernardi, A., & Galgaro, A. (2021). Evaluation of the Effect of Anti-Corrosion Coatings on the Thermal Resistance of Ground Heat Exchangers for Shallow Geothermal Applications. Energies, 14(9), 2586. https://doi.org/10.3390/en14092586