Operation Optimization Based on the Power Supply and Storage Capacity of an Active Distribution Network

Abstract

Due to the interconnection and active management of Distributed Generation (DG) and Energy Storage Systems (ESSs), the traditional electrical distribution network has become an Active Distribution Network (ADN), posing challenges to the operation optimization of the network. The power supply and storage capacity indexes of a Local Autonomy Control Region (LACR), which consists of DGs, ESSs and the network, are proposed in this paper to quantify the power regulating range of a LACR. DG/ESS and the network are considered as a whole in the model of the indexes, considering both network constraints and power constraints of the DG/ESS. The index quantifies the maximum LACR power supplied to or received from ADN lines. Similarly, power supply and storage capacity indexes of the ADN line are also proposed to quantify the maximum power exchanged between ADN lines. Then a practical algorithm to calculate the indexes is presented, and an operation optimization model is proposed based on the indexes to maximum the economic benefit of DG/ESS. In the optimization model, the power supply reliability of the ADN line is also considered. Finally, the indexes of power supply and storage capacity and the optimization are demonstrated in a case study.

1. Introduction

Various kinds of renewable energy have been so far integrated into electrical power distribution networks in the form of Distributed Generation (DG) systems to reduce societys’ dependence on fuel resources. Meanwhile, Energy Storage Systems (ESSs) are also connected to the network. The grid-connected DGs and ESSs greatly change the characteristics of the network and complicate the operation optimization, and the intermittence of renewable energy poses risks to the operation of the whole network. To address these issues, active management of the network and DGs/ESSs has been broadly utilized, suppressing the intermittence of the renewable energy and reducing the peak-valley differences of the loads. The active management also puts off the upgrade of power facilities [1,2], improves the power supply reliability, and results in the conversion of the traditional distribution network into an Active Distribution Network (ADN).

To date, abundant research have been done on the active management and operation optimization of grid-connected DGs/ESSs. Some forms of renewable energy, e.g., wind generation and photovoltaic arrays, etc., are intermittent and thus increase the fluctuation of the net load of the ADN lines. High power density ESS [3,4] has been utilized to suppress the short-term power fluctuation, while high energy density ESS is utilized to smooth the renewable energy power in the long term [5,6], as well as reduce the peak-valley load differences of ADN lines [7,8]. Hybrid storage systems, consisting of both high power density ESS and high energy density ESS, by combining the merits from these two types of the ESS, are regarded as more advantageous [9,10,11]. The real-time control of ESSs suppresses the impact of intermittent energy sources on the network, however, operation optimization of the whole network should be considered in the real-time control of ESS. Different ADN optimization models considering the line losses or electricity costs are presented in [12,13], and optimization strategies are discussed in [14,15] for the operation of combined heating, cooling and power systems. Since the powers of individual DGs/ESSs are the variables that need to be optimized in the optimization, the computation cost increases rapidly with the number of DGs/ESSs considered. Moreover, various kinds of DGs, ESSs, loads and networks are combined into a system, which is able to actively regulate its power. The power regulating ability is one of the key distinctions of ADNs from traditional distribution networks, and this has not been well studied yet.

In this work, the power supply and storage capacity of the network is analyzed, and a long-term operation optimization model is proposed based on the capacity to maximize the DG/ESS economic benefits. Within an ADN line, the Local Autonomy Control Region (LACR), which consists of DGs/ESSs, loads and network, is operated as a whole. The power supply & storage capacity index of the LACR is proposed to quantify the maximum power regulation range of the LACR, considering both the DG/ESS power constraints and the network restrictions. The power supply and storage capacity index of an ADN line is also presented to quantify the maximum power exchanged between adjacent ADN lines through tie switches. Practical algorithms are used to calculate the power supply and storage indexes, and an operation optimization model of an ADN line based on the indexes is proposed to maximize the economic benefits of DG/ESS. The power supply reliability of the ADN line is also considered in the optimization. Finally the indexes of power supply and storage capacity and the optimization are demonstrated in a case study.

2. Power Supply & Storage Capacity of Local Autonomy Control Region

According to the survey of the CIGRE C6.11 working group, active distribution networks are distribution networks that have systems in place to control a combination of Distributed Energy Resources (DERs) [16], and have the ability to manage the electricity flows. With the active management of DERs and electricity flows, feeders of the traditional distribution network are converted to ADN lines. Within an ADN line, part of the DERs and loads make up a Local Autonomy Control Region which is managed and operated as a whole to reduce the optimization computation cost and relieve the communication pressure between the control center and DERs [17,18]. As shown in Figure 1, three LACRs exist in ADN line A and line B. The area of the LACR is generally specified according to the topological connection and the allocation of the autonomic controller. The branch with an autonomic controller and more than one DER is regard as a LACR. The autonomic controller receives the control target of the whole LACR from the control center, and coordinates the operation of DERs within the LACR, according to that control target.

Figure 1. ADN line and local autonomy control region.

Figure 1. ADN line and local autonomy control region.

The maximum export/import power of LACR needs to be calculated so that the LACR could be regarded as a whole in the operation optimization of the ADN line. The power supply and storage capacity of the LACR is defined as the maximum export/import real power of the LACR, considering power constraints of DGs/ESSs as well as any restrictions of node voltage and maximum branch current. The power supply capacity of the LACR is the maximum export power (power α in Figure 1), whose positive direction is defined as injecting into an ADN line, while the power storage capacity is the maximum import power of LACR (power β in Figure 1), whose positive direction is defined as injecting into the LACR. The power constraints of DGs/ESSs, node voltage restrictions, branch current and SOC of ESSs are considered in the calculation of the capacity, as discussed below.

2.1. Power Constraints of Distributed Generation

DGs can be classified into two categories according to their power controllablity: power controllable DGs and uncontrollable DGs. The power of biomass power generators, micro gas turbines or fuel cells is controllable, while the wind generation and photovoltaic cell power is intermittent and dependent on the weather. The power restrictions of the two types of DG are shown in Equation (1):

(1)

where F_ctrl is the set of power controllable DGs; P_i is the power of the i^th power-controllable DG; while and are the minimum operating power and the rated power; F_inte is the set of power uncontrollable DGs; P_j is the power of j^th power-uncontrollable DG; and is the expected maximum power according to the weather forecast. Some of the intermittent renewable energy generators have the ability to adjusting the power by changing the operating point, but in order to maximize the exploitation of renewable energy, the renewable energy generators are assumed to be operated at their maximum power point according to the power forecasting.

2.2. Power Constraints of Energy Storage System

The charging/discharging power of an ESS is subjected to both constraints of rated power and constraints of the ESS’ SOC. The change of SOC during charging/discharging is calculated by Equation (2):

(2)

where ΔS_oc(ΔT) is the change of SOC during time period of [T,T + ΔT]; μ and η are charging/discharging efficiencies respectively; P_c and P_d are charging/discharging power; E_R is the rated energy capacity of the ESS.

As excessive charging or discharging may cause damage to the ESS, Equation (3) should be satisfied:

(3)

where S_oc(T) is the SOC at time T; while and are the upper and lower limitation of SOC respectively. After the charging/discharging in the time interval [T,T + ΔT], the value of SOC at T + ΔT should satisfy the Inequation (3). Then Inequation (4) is derived according to Equations (2) and (3), ignoring the power changes during [T,T + ΔT]. The symbols in Equation (4) have the same meaning with those in Equations (2) and (3):

(4)

The power constraints of ESS are shown as Equation (5), considering constraints of both SOC and rated charging/discharging power. and are the rated charging/discharging power, and are the maximum charging/discharging power calculated according to the constraints:

(5)

2.3. The Model of Power Supply & Storage Capacity of Local Autonomy Control Region

The power supply and storage capacity of a LACR is the maximum power that the LACR can supply to or receive from an ADN line, considering both the power constraints of the DG/ESS and constraints of node voltages and branch currents. The model of the capacity is given by Equations (6)–(8), in which, Equations (6) and (7) are the objective functions and Equation (8) are the constraints:

(6)

(7)

(8)

In Equations (6) and (7), , are the power supply and storage capacity to be calculated. The computations of “∑”, “+”, “−” are calculated by the power flow method, in which network losses are considered. F_ESS is the set of ESSs inside the LACR, and F_L is the set of loads. P_c,k and P_d,k are the charging and discharging power of the k^th ESS. P_l is the power of l^th load.

Equation (8a) is the node voltage restriction, where V_max and V_min are the upper and lower node voltage limitations. Equation (8b) is the branch current restriction, where I_b,Rated is the rated maximum current of the b^th branch. Equation (8c) is the power constraint of power controllable DGs, and Equations (8d,e) are charging/discharging power constrains of ESSs.

The positive direction of the power supply capacity of the LACR is defined as power injected into the ADN line, while that of the power storage capacity is defined as power received from the ADN line. A LACR may have the characteristics of power controllable DGs, power controllable loads or storage systems, according to the value of its power supply and storage capacity.

As shown in Figure 2, positive power supply capacity and negative storage capacity indicate that the maximum power supplied by DGs/ESSs in the LACR is greater than the power of loads, and the LACR has the characteristic of power controllable DGs. On the contrary, negative power supply capacity and positive storage capacity means that the maximum power supplied by DGs/ESSs is smaller than the power of loads, and the LACR has the power controllable load characteristics. Besides, if both power supply capacity and storage capacity are positive, the power regulating range of the LACR is large, and the LACR is regarded as having the energy storage system characteristics.

Figure 2. Characteristics of a LACR according to the power supply/storage capacity.

Figure 2. Characteristics of a LACR according to the power supply/storage capacity.

3. The Power Supply & Storage Capacity of ADN Line

The power supply and storage capacity of an ADN line denotes the maximum power exchanged between adjacent ADN lines, as shown in Figure 3. In Figure 3a, since a fault occurs in line B, the load of line B is transferred to line A by closing tie switch I-II, and the power supply capacity of line A indicates the maximum power supplied to the ADN line B through the two tie switches. Supposing excessive renewable energy exists in line B, as shown in Figure 3b, then in order to maximize the exploitation of the renewable energy, the network is reconfigured and the excessive renewable energy of line B is consumed or stored by line A. The power storage capacity of line A indicates the maximum power injected into line A through tie switch I-II by line B.

Figure 3. (a) Power supply capacity of ADN line; (b) Power storage capacity of ADN line.

Figure 3. (a) Power supply capacity of ADN line; (b) Power storage capacity of ADN line.

In Figure 3 there is more than one tie switch between the ADN lines, and the power supply and storage capacity is the maximum summation of the power transmitted by all the tie switches. If there is no adjacent line, the power supply and storage capacity of ADN line is 0.

The model of power supply and storage capacity of ADN line is shown in Equations (9)–(11):

(9)

(10)

Subject to:

$$\{\begin{array}{ll}{V}_{\min }\le V\le V_{\max }\hfill & \left(\mathrm{a}\right)\hfill \\ I_b\le I_{b.Rated}\hfill & \left(\mathrm{b}\right)\hfill \\ -P_{\text{st.m}}^{\max }\le P_m\le P_{\text{su.m}}^{\max }\hfill & \left(\mathrm{c}\right)\hfill \\ P_B\ge 0\hfill & \left(\mathrm{d}\right)\hfill \end{array}$$

(11)

where and are the supply capability and storage capability of ADN line; P_B is the power injected into ADN line by high-voltage distribution network; P_m is the power of m^th LACR, whose positive direction is defined as injecting into the ADN line; P_i is the power of the loads outside the LACR. Equations (11a,b) are the constraints of node voltage and branch current. Equation (11c) is the power restriction of the LACR, and , are the power supply capability and storage capability of the m^th LACR, respectively, which are calculated by Equations (6) and (7). Equation (11d) is the power constraint of the high-voltage grid. The power of the high-voltage grid injected into ADN line should be positive. The network loss is considered in the computation of “∑”, “+” and “−”. Other symbols in Equations (9)–(11) have the same meaning as those in Equations (6)–(8).

4. Algorithm of the Power Supply & Storage Capacity of the LACR and ADN Line

The power supply and storage capacity of the LACR and ADN line are proposed in order to reduce the calculation costs and complexity of the operation optimization of DGs/ESSs and ADN lines. Therefore the algorithm used for calculating the capacity should be practical.

Both the node voltage and branch current of the network will change with the DG/ESS power. As the constraints of node voltage and branch current are considered in the model of power supply and storage capacity, the change of voltage and current caused by DGs/ESSs need to be quantified.

The voltage deviation rate [19] of the network is defined in Equation (12), which indicates the voltage deviation of all the nodes in the network from the nominal voltage:

(12)

where Ui and P_i are the voltage and real power of i^th node; M is the count of nodes in the network; U_nom is the nominal voltage, while U_min and U_max are the lower and upper limitation of the voltage according to the voltage quality standard. U_nom, U_min and U_max are constants. Taking a medium distribution network for instance, $U_{nom}=10\text{ kV}$, $U_{\min }=10\text{ kV}\times 95\%$ and $U_{\max }=10\text{ kV}\times 105\%$. |P_i| is regarded as the weight of the voltage deviation of the i^th node. The smaller the voltage deviation of the nodes in the network, the smaller the value of RD, and RD will be 0 if the voltage of all the nodes is equal to the nominal voltage. The loading rate of the network is defined in Equation (13), which indicates the mean loading rate of all the cables and overhead conductors in the network:

(13)

where I_j is the current of j^th conductor; and I_j,max is the rated maximum current of the conductor; RL is the mean loading rate of the whole network.

The value of RD and RL will change with the power of DG/ESS, and the changes of RD and RL are regards as the impact of DG/ESS on the network. The impact factor of k^th DG/ESS is defined as Equation (14), in which, ΔP_k is the power change of the k^th DG/ESS, ΔRD and ΔRL denote the changes of RD and RL caused by ΔP_k:

C_k = (ΔRD + ΔRL)/ΔP_k

(14)

The impact factor is different for different DGs/ESSs. The value of C_k is dependent on the topological connection of the DGs/ESSs and the branch current of the network.

A stepwise optimization method is implemented to calculate the power supply and storage capacity. The power of DG/ESS is initialized to 0, then a loop is started, in which the impact factors os DGs/ESSs on the network are calculated and the power of the DG/ESS with the minimum impact factor is increased by one power step. Constraints are verified in the loop, and the loop will stop if the constraints are not satisfied. The algorithm processes for power supply and storage capacity of the LACR and ADN line are discussed below.

4.1. Algorithm of Power Supply and Storage Capacity of the LACR

In the proposed algorithm procedure, the DGs/ESSs in LACRs are sorted according to their impact factor on the network, and the power of the DG/ESS with the minimum impact factor is increased by one power step. The constraints in Equation (8) are also verified in the loop. The algorithm procedure of the power supply capacity of LACR is described as follows:

(1)

Initialization. The power of all DGs/ESSs in the LACR is initialized to 0, and the upper and lower limitation of DGs’/ESSs’ power are calculated according to the power constraints discussed in Section 2.1 and Section 2.2. A list is created which consists of all the DGs/ESSs inside the LACR, and the loop starts.

(2)

The impact factors of each DG/ESS are calculated according to Equation (14).

(3)

The DGs/ESSs in the list created in step (1) are sorted according to their impact factors. The power of the DG/ESS with the minimum impact factor is increased by one power step.

(4)

Constraints Verification. The constraints stated in Equation (8) are verified in the loop. If any constraint cannot be satisfied, cancel the power increment in step (3), and remove the DG/ESS from the list.

(5)

If all the DGs/ESSs are removed from the list, the loop stops and go to step (6), else go to step (2).

(6)

Power flow algorithm is executed to calculate the total power of the LACR supplied to the ADN line which is the power supply capacity of the LACR.

The block diagram of the power supply capacity calculation of the LACR is depicted in Figure 4. The calculation process of the power storage capacity of the LACR is similar to that of the power supply capacity, while the different exists in the step (3): the power of DG/ESS with the minimum impact factor decreases by one step or the discharging power increases.

Figure 4. Block diagram of calculating the power supply capacity of the LACR.

Figure 4. Block diagram of calculating the power supply capacity of the LACR.

4.2. Algorithm of the Power Supply & Storage Capacity of ADN Line

The power supply capacity of the ADN line is equal to the maximum power supplied to an adjacent line through a closed tie switch. In order to calculate the power supply capacity of an ADN line, the adjacent line is assumed to be a virtual power-controllable load, and P_V is used to represent the power of the virtual load. During the iterations, the value of P_V increases step by step and the constraints stated in Equation (11) are verified. If any of the constraints is not satisfied, the loop stops and the value of power supply capacity of ADN line is equal to P_V. If there is more than one tie switch between the two ADN lines, the adjacent line is assumed to be the same amount of virtual power-controllable load, and the power supply capacity is equal to the maximum total power of all virtual loads.

Figure 5. Block diagram of calculating the power supply capacity of an ADN line.

Figure 5. Block diagram of calculating the power supply capacity of an ADN line.

The process of the algorithm is shown in Figure 5. The iteration process of computing the power storage capacity of an ADN line is similar to that of power supply capacity, while a difference exists in the assumption of the adjacent line. The adjacent line is assumed to be a virtual energy source (P-Q bus), and the maximum power of the virtual energy source is the power storage capacity of the ADN line.

5. Operation Optimization of an ADN Considering the Power Supply Reliability Based on the Power Supply and Storage Capacity

An operation optimization model is proposed in this section based on the aforementioned power supply and storage capacity of an LACR and ADN lines. With the active management of power controllable DGs and ESSs, the operation optimization of ADN brings economic benefits. The requirement for the network backup capacity will be reduced with the reduction of load peak-valley differences. The investment of upgrading the power facilities are postponed with the peak shaving, and the network losses are also reduced. The objective of the operation optimization in this paper is to maximize the economic benefits of ADN during 24 h. The LACR in the ADN line is operated as a whole, and the power of the LACR in 24 h is the variable to be optimized.

The economic benefit is calculated as Equation (15), in which the benefit consists of four parts: reduction of peak shaving cost, generation benefit of DGs, reduction of the network loss and the benefit of ESS charging/discharging at different electricity prices:

(15)

In Equation (15) E_ps is the energy of peak shaving of DG/ESS; and p_ps is the peak shaving cost of the grid; E_D,g is the energy generated by power controllable DG; and p(t) ΔE_loss is electricity price at time t; is the reduction of the network loss; is the energy discharged by ESS. A positive value of denotes discharged energy, while a negative value denotes charged energy.

The power supply reliability of an ADN line is considered in the optimization. When a fault occurs in an ADN line, the network is reconfigured, and the load of the faulty line is transferred to adjacent lines [20]. The maximum load transfer capacity of the ADN line is quantified by its power supply capacity according to the definition of the power supply capacity of the ADN line. Therefore, the constraint of power supply reliability is expressed as Equation (17a), in which is the power supply capacity of the ADN line at time t, and P_R is the outage load that needed to be transferred. The optimization model is shown by Equations (16) and (17):

(16)

(17)

The symbols in Equation (16) have the same meaning as those in Equation (15). Equation (17a) is the constraint of power supply reliability, and Equation (17b) is the power constraint of the k^th LACR. P_k(t) is the power of the k^th LACR at time t, and the positive direction of is to inject into the ADN line. , are the power supply/storage capacity of the k^th LACR, which are the upper and lower limitations of P_k(t). Equations (17c,d) are the constraints of node voltage and branch current. Since the LACR is operated as a whole, the count of variables to be optimized is reduced. The power supply and storage capacity quantifies the power regulating range of the LACR and the maximum power supplied to adjacent lines, which reduces the count of constraints. Accordingly, the computation cost and complexity are reduced by applying the power supply and storage capacity in the optimization model.

6. Case Study

The methodology presented in this paper is tested using a 10 kV active distribution network with three DGs, two ESSs and 22 loads, as shown in Figure 6. The network consists of two lines: line A and line B, and the two lines are connected together through one tie switch. Two LACRs exist in line A, and the rated maximum apparent power of the wires in the network is 4 MVA. The objective of line A’s operation optimization is to maximize the economic benefits. The power supply reliability of line B is considered in the optimization of line A, and the load of line B will be transferred to line A if fault occurs at line B. The optimization model is given by Equations (16) and (17).

Figure 6. Topological connection of ADN.

Figure 6. Topological connection of ADN.

The electrical specifications of the DGs/ESSs are shown in Table 1. ES1, ES2 and MT are dispatchable. The minimum operating power of MT is 10 kW, and the contract energy generated in 24 h is 2000 kWh. ES1 and ES2 are sodium-sulphur battery (NAS) energy storage systems. In practice, NAS batteries are limited to discharge less than 90% of their theoretical capacity to limit the corrosive properties of the material [21]. Correspondingly the upper and lower limitations of SOC in this case are set to 95% and 10%, respectively. The wind generation power is dependent upon wind speed, as shown in Figure 7. The electricity price is 0.68 CNY/kWh during the time [9,22], and is 0.33 CNY/kWh for the rest of the time. [17,19] period is peak time while [5,7] is the valley time. The peak shaving cost of the grid is 0.167 CNY/kWh [22].

Table 1. Electrical specifications of the DGs/ESSs.

Name	Type	Rated power	Energy capacity	Min operating power
ES1	NAS battery energy storage	300 kW	2400 kWh	0
ES2	NAS battery energy storage	200 kW	1600 kWh	0
MT	Micro turbine	280 kW	-	10 kW
WG1	Wind generation	500 kW	-	-
WG2	Wind generation	1000 kW	-	-

Table 1. Electrical specifications of the DGs/ESSs.

Name	Type	Rated power	Energy capacity	Min operating power
ES1	NAS battery energy storage	300 kW	2400 kWh	0
ES2	NAS battery energy storage	200 kW	1600 kWh	0
MT	Micro turbine	280 kW	-	10 kW
WG1	Wind generation	500 kW	-	-
WG2	Wind generation	1000 kW	-	-

Figure 7. Load of ADN and power of wind generator.

Figure 7. Load of ADN and power of wind generator.

The total load of ADN lines and the power of wind generations during 24 h are shown in Figure 7. The peak and valley load of line A are 3.65 MW and 1.65 MW, respectively, and the mean load is 2.61 MW. The mean square error of the load is 3.15 × 10¹¹. The power intermittence of wind generation increases the power fluctuation of line A. A genetic algorithm is implemented to solve the optimization. Figure 8 shows the optimum result of the charging/discharging power and SOC of ES1, ES2.

Figure 8. (a) Power of ES1 and ES2 after the optimization; (b) SOC of ES1 and ES2.

Figure 8. (a) Power of ES1 and ES2 after the optimization; (b) SOC of ES1 and ES2.

As shown in Figure 8, ES1 and ES2 charge during [0,8], and discharge during [10,23], maximizing the benefits of charging/discharging at different electricity prices. The discharging power reaches the rated ESS discharging power during the peak time, and the charging power reaches the rated charging power during the valley time, maximizing the energy of peak shaving.

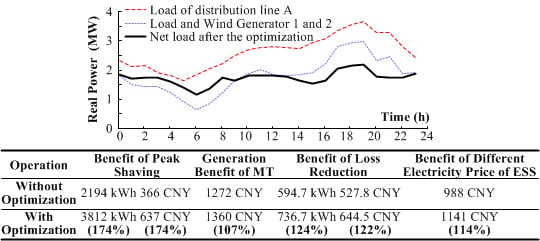
Figure 9 shows the power of MT and the net load of line A after the optimization. As the contract energy of MT generated in 24 h is 2000 kWh, MT stops when the electricity price is 0.33 in order to maximize the benefit of electricity generation, and operates at its rated power during the peak time to maximize the energy of peak shaving. The peak-valley difference of the net load of line A is reduced from 2.33 MW to 1.05 MW after the optimization, as shown in Figure 9b.

Figure 9. (a) Power of MT after the optimization; (b) Net load of line A after the optimization.

Figure 9. (a) Power of MT after the optimization; (b) Net load of line A after the optimization.

Without the operation optimization, ES1 and ES2 are assumed to charge/discharge at constant power considering the electricity price, and MT also operates at constant power during [7,23], as shown in Figure 10. The economic benefits of ADN with/without optimization are compared in Table 2.

Figure 10. Operations of ES1, ES2 and MT without optimization.

Figure 10. Operations of ES1, ES2 and MT without optimization.

Table 2. Comparison of economic benefits with/without the optimization.

Operation	Benefit of peak shaving		Generation benefit of MT	Benefit of loss reduction		Benefit of electricity price difference of ESS
Without optimization	2194 kWh	366 CNY	1272 CNY	594.7 kWh	527.8 CNY	998 CNY
With optimization	3812 kWh (174%)	637 CNY (174%)	1360 CNY (107%)	736.7 kWh (124%)	644.5 CNY (122%)	1141 CNY (114%)

Table 2. Comparison of economic benefits with/without the optimization.

Operation	Benefit of peak shaving		Generation benefit of MT	Benefit of loss reduction		Benefit of electricity price difference of ESS
Without optimization	2194 kWh	366 CNY	1272 CNY	594.7 kWh	527.8 CNY	998 CNY
With optimization	3812 kWh (174%)	637 CNY (174%)	1360 CNY (107%)	736.7 kWh (124%)	644.5 CNY (122%)	1141 CNY (114%)

Compared with the operation without optimization, the benefits of peak shaving and loss reduction increase by 74% and 22%. The generation benefit of MT and benefit of electricity price difference of ESS increase by only 7% and 14%, that is because the change of electricity price has already been considered in the operation of ESSs and MT without optimization, as shown in Figure 10. The total benefit is 3782 CNY after the optimization, while that is 3163 CNY before the optimization.

The power supply & storage capacity of LACR1 and LACR2 in the optimization are shown in Figure 11. The optimized power of LACR1 and LACR2 are regulated within the power adjustable ranges determined by their power supply and storage capacity, and the Constraint (17b) is satisfied. The load is light in LACR1, and is less than the power of ES1 and WG1. Both of the power supply capacity and storage capacity of LACR1 are positive most of the time, as shown in Figure 11a, and LACR1 has energy storage system characteristics. LACR2 consists of ES2, MT and WG2, and the load is heavy in LACR2. The power supply capacity of LACR2 is negative most of the time, as shown in Figure 11b, and LACR2 has power controllable load characteristics.

Figure 11. (a) Power supply and storage capacity and actual power of LACR1; (b) Power supply & storage capacity and actual power of LACR2.

Figure 11. (a) Power supply and storage capacity and actual power of LACR1; (b) Power supply & storage capacity and actual power of LACR2.

Power supply reliability is considered in the optimization. The power supply capacity of line A before and after the optimization are calculated, as shown in Figure 12. The fault is assumed to occur at the outlet breaker of line B, and all the loads of line B need to be transferred to line A. During the time period [18,20] the loads of both line A and line B are heavy, and the power supply capacity of line A before the optimization cannot meet the requirement of the load transfer of line B. The operation optimization increases the power supply capacity of line A during the peak hours, and consequently the constraint of power supply reliability is satisfied.

Figure 12. Power supply capacity of ADN Line A after optimization.

Figure 12. Power supply capacity of ADN Line A after optimization.

The computation cost of the optimization based on the power supply and storage capacity of the ADN is compared with that based on individual DGs/ESSs, as shown in Table 3. Both the optimization models are resolved by a genetic algorithm. Since the application of power supply and storage capacity reduces the number of variables and constraints in the optimization model, the number of iterations of the algorithm is reduced obviously (from 162 to 103). The power supply and storage capacity are calculated in the iteration of the algorithm, which increases the calculation time of the single cycle in the iteration. However, the total calculation time of the optimization based on power supply and storage capacity is reduced (from 215 s to 187 s).

Table 3. Computation cost comparison of the optimization in different models.

Optimization model	Algorithm	Number of iterations	Calculation time
Based on individual DG/ESS, without power supply &storage capacity	GA	162	215 s
Based on power supply & storage capacity	GA	103 (63.2%)	187 s (87.0%)

Table 3. Computation cost comparison of the optimization in different models.

Optimization model	Algorithm	Number of iterations	Calculation time
Based on individual DG/ESS, without power supply &storage capacity	GA	162	215 s
Based on power supply & storage capacity	GA	103 (63.2%)	187 s (87.0%)

The calculation time is reduced by 13% with the application of power supply and storage capacity in the study case, in which there are only two ESSs and one DG to be optimized. As the number of DGs/ESSs increases, the benefit of applying the power supply and storage capacity will be more significant.

7. Conclusions

Grid-connected DGs and ESSs endow the distribution network with the ability of managing the electricity flows. Since the operation is subject to both DG’s/ESS’s electrical specifications and network constraints, the complexity of the operation optimization of an ADN is greatly increased with the number of DGs/ESSs. In this work, power supply and storage capacity indexes of a Local Autonomy Control Region are proposed to quantify the power regulating range of the LACR, considering both the power constraints of DGs/ESSs and network constraints. Similarly, the power supply and storage capacity indexes of an ADN line are presented to quantify the maximum power that can be exchanged between adjacent lines through tie switches. Afterwards, practical calculation methods are proposed for the indexes of LACR and ADN lines. Then the operation optimization of an ADN is proposed based on the indexes, which is proved effective by a study case.

The application of power supply and storage capacity indexes of a LACR can reduce the number of variables to be optimized in the optimization model. The number of constraints in the optimization model is also reduced since the power constraints of DGs/ESSs and network restrictions inside the LACR have already been considered in the model of the indexes. The power supply and storage capacity of an ADN line quantifies the maximum power that can be exchanged between ADN lines, which simplifies the power supply reliability constraint. In conclusion, both the computation cost and the complexity of the optimization model are reduced by applying the power supply and storage capacity.