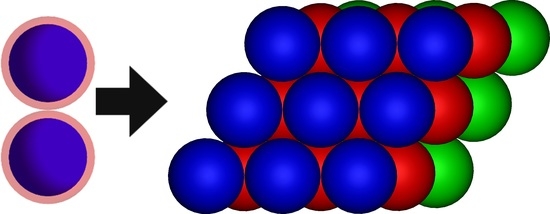
Low-Temperature Crystal Structures of the Hard Core Square Shoulder Model
Abstract
:1. Introduction
2. Model and Simulation Methods
2.1. Crystal Structure Prediction
2.2. Crystal Free Energies
Fluid Free Energy
3. Results
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Frenkel, D.; Wales, D.J. Colloidal self-assembly: Designed to yield. Nat. Mater. 2011, 10, 410–411. [Google Scholar] [CrossRef] [PubMed]
- Vogel, N.; Retsch, M.; Fustin, C.A.; del Campo, A.; Jonas, U. Advances in colloidal assembly: The design of structure and hierarchy in two and three dimensions. Chem. Rev. 2015, 115, 6265–6311. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Lu, F.; Yager, K.G.; Van Der Lelie, D.; Gang, O. A general strategy for the DNA-mediated self-assembly of functional nanoparticles into heterogeneous systems. Nat. Nanotechnol. 2013, 8, 865–872. [Google Scholar] [CrossRef] [PubMed]
- Kodger, T.E.; Guerra, R.E.; Sprakel, J. Precise colloids with tunable interactions for confocal microscopy. Sci. Rep. 2015, 5. [Google Scholar] [CrossRef] [PubMed]
- Yethiraj, A.; van Blaaderen, A. A colloidal model system with an interaction tunable from hard sphere to soft and dipolar. Nature 2003, 421, 513–517. [Google Scholar] [CrossRef] [PubMed]
- Löwen, H. Introduction to colloidal dispersions in external fields. Eur. Phys. J. Spec. Top. 2013, 222, 2727–2737. [Google Scholar] [CrossRef]
- Grzelczak, M.; Vermant, J.; Furst, E.M.; Liz-Marzán, L.M. Directed self-assembly of nanoparticles. ACS Nano 2010, 4, 3591–3605. [Google Scholar] [CrossRef] [PubMed]
- Dinsmore, A.D.; Crocker, J.C.; Yodh, A.G. Self-assembly of colloidal crystals. Curr. Opin. Colloid Interface Sci. 1998, 3, 5–11. [Google Scholar] [CrossRef]
- Palberg, T. Crystallization kinetics of repulsive colloidal spheres. J. Phys. Condens. Matter 1999, 11, R323. [Google Scholar] [CrossRef]
- Ivlev, A.; Löwen, H.; Morfill, G.; Royall, C.P. Complex Plasmas and Colloidal Dispersions: Particle-Resolved Studies of Classical Liquids and Solids; World Scientific, Series in Soft Condensed Matter; World Scientific Publishing: Hackensack, NJ, USA, 2012; Volume 5. [Google Scholar]
- Meijer, J.M.; Hagemans, F.; Rossi, L.; Byelov, D.V.; Castillo, S.I.; Snigirev, A.; Snigireva, I.; Philipse, A.P.; Petukhov, A.V. Self-assembly of colloidal cubes via vertical deposition. Langmuir 2012, 28, 7631–7638. [Google Scholar] [CrossRef] [PubMed]
- Vroege, G.J.; Lekkerkerker, H.N. Phase transitions in lyotropic colloidal and polymer liquid crystals. Rep. Prog. Phys. 1992, 55, 1241. [Google Scholar] [CrossRef]
- Op Reinink, A.L.; van den Pol, E.; Petukhov, A.; Vroege, G.; Lekkerkerker, H. Phase behaviour of lyotropic liquid crystals in external fields and confinement. Eur. Phys. J. Spec. Top. 2013, 222, 3053–3069. [Google Scholar] [CrossRef]
- Lahtinen, T.; Haataja, J.S.; Tero, T.R.; Häkkinen, H.; Ikkala, O. Template-Free Supracolloidal Self-Assembly of Atomically Precise Gold Nanoclusters: From 2D Colloidal Crystals to Spherical Capsids. Angew. Chem. Int. Ed. 2016, 55, 16035–16038. [Google Scholar]
- Watzlawek, M.; Likos, C.N.; Löwen, H. Phase diagram of star polymer solutions. Phys. Rev. Lett. 1999, 82, 5289. [Google Scholar] [CrossRef]
- Likos, C.N.; Hoffmann, N.; Löwen, H.; Louis, A.A. Exotic fluids and crystals of soft polymeric colloids. J. Phys. Condens. Matter 2002, 14, 7681. [Google Scholar] [CrossRef]
- Ziherl, P.; Kamien, R.D. Maximizing Entropy by Minimizing Area: Towards a New Principle of Self-Organization. J. Phys. Chem. B 2001, 105, 10147–10158. [Google Scholar] [CrossRef]
- Barkan, K.; Diamant, H.; Lifshitz, R. Stability of quasicrystals composed of soft isotropic particles. Phys. Rev. B 2011, 83, 172201. [Google Scholar] [CrossRef]
- Denton, A.; Löwen, H. Stability of colloidal quasicrystals. Phys. Rev. Lett. 1998, 81, 469. [Google Scholar] [CrossRef]
- Dotera, T.; Oshiro, T.; Ziherl, P. Mosaic two-lengthscale quasicrystals. Nature 2014, 506, 208–211. [Google Scholar] [CrossRef] [PubMed]
- Sakya, P.; Seddon, J.M.; Templer, R.H.; Mirkin, R.J.; Tiddy, G.J.T. Micellar cubic phases and their structural relationships: The nonionic surfactant system C12EO12/water. Langmuir 1997, 13, 3706–3714. [Google Scholar] [CrossRef]
- Ungar, G.; Liu, Y.; Zeng, X.; Percec, V.; Cho, W.D. Giant supramolecular liquid crystal lattice. Science 2003, 299, 1208–1211. [Google Scholar] [CrossRef] [PubMed]
- Lee, S.; Leighton, C.; Bates, F.S. Sphericity and symmetry breaking in the formation of Frank–Kasper phases from one component materials. Proc. Natl. Acad. Sci. USA 2014, 111, 17723–17731. [Google Scholar] [CrossRef] [PubMed]
- Hajiw, S.; Pansu, B.; Sadoc, J.F. Evidence for a C14 Frank–Kasper phase in one-size gold nanoparticle superlattices. ACS Nano 2015, 9, 8116–8121. [Google Scholar] [CrossRef] [PubMed]
- Goodfellow, B.W.; Rasch, M.R.; Hessel, C.M.; Patel, R.N.; Smilgies, D.M.; Korgel, B.A. Ordered structure rearrangements in heated gold nanocrystal superlattices. Nano Lett. 2013, 13, 5710–5714. [Google Scholar] [CrossRef] [PubMed]
- Kuttner, C.; Chanana, M.; Karg, M.; Fery, A. Macromolecular Decoration of Nanoparticles for Guiding Self-Assembly in 2D and 3D; Wiley-VCH: Weinheim, Germany, 2016. [Google Scholar]
- Boles, M.A.; Engel, M.; Talapin, D.V. Self-assembly of colloidal nanocrystals: From intricate structures to functional materials. Chem. Rev. 2016, 116, 11220–11289. [Google Scholar] [CrossRef] [PubMed]
- Pattabhiraman, H.; Gantapara, A.P.; Dijkstra, M. On the stability of a quasicrystal and its crystalline approximant in a system of hard disks with a soft corona. J. Chem. Phys. 2015, 143, 164905. [Google Scholar] [CrossRef] [PubMed]
- Pattabhiraman, H.; Dijkstra, M. Phase behaviour of quasicrystal forming systems of core-corona particles. J. Chem. Phys. 2017, 146, 114901. [Google Scholar] [CrossRef] [PubMed]
- Malescio, G.; Pellicane, G. Stripe phases from isotropic repulsive interactions. Nat. Mater. 2003, 2, 97–100. [Google Scholar] [CrossRef] [PubMed]
- Fornleitner, J.; Kahl, G. Pattern formation in two-dimensional square-shoulder systems. J. Phys. Condens. Matter 2010, 22, 104118. [Google Scholar] [CrossRef] [PubMed]
- Yuste, S.B.; Santos, A.; López de Haro, M. Structure of the square-shoulder fluid. Mol. Phys. 2011, 109, 987–995. [Google Scholar] [CrossRef]
- Buldyrev, S.V.; Malescio, G.; Angell, C.A.; Giovambattista, N.; Prestipino, S.; Saija, F.; Stanley, H.E.; Xu, L. Unusual phase behavior of one-component systems with two-scale isotropic interactions. J. Phys. Condens. Matter 2009, 21, 504106. [Google Scholar] [CrossRef] [PubMed]
- Heyes, D.M.; Aston, P.J. Square-well and square-shoulder fluids: Simulation and equations of state. J. Chem. Phys. 1992, 97, 5738–5748. [Google Scholar] [CrossRef]
- Bordin, J.R.; Barbosa, M.C. Brownian dynamics leads to two waterlike anomalous regions in a 2D core-softened potential. arXiv, 2017; arXiv:1709.05512. [Google Scholar]
- Sperl, M.; Zaccarelli, E.; Sciortino, F.; Kumar, P.; Stanley, H.E. Disconnected Glass-Glass Transitions and Diffusion Anomalies in a model with two repulsive length scales. Phys. Rev. Lett. 2010, 104, 145701. [Google Scholar] [CrossRef] [PubMed]
- Kincaid, J.M.; Stell, G.; Goldmark, E. Isostructural phase transitions due to core collapse. II. A three-dimensional model with a solid–solid critical point. J. Chem. Phys. 1976, 65, 2172–2179. [Google Scholar] [CrossRef]
- Bolhuis, P.; Frenkel, D. Isostructural solid-solid transitions in systems with a Repulsiveshoulder’potential. J. Phys. Condens. Matter 1997, 9, 381–387. [Google Scholar] [CrossRef]
- Denton, A.; Löwen, H. Isostructural solid-solid transitions in square-shoulder systems. J. Phys. Condens. Matter 1997, 9, L1. [Google Scholar] [CrossRef]
- Pauschenwein, G.J.; Kahl, G. Clusters, columns, and lamellae—Minimum energy configurations in core softened potentials. Soft Matter 2008, 4, 1396–1399. [Google Scholar] [CrossRef]
- Pauschenwein, G.J.; Kahl, G. Zero temperature phase diagram of the square-shoulder system. J. Chem. Phys. 2008, 129, 174107. [Google Scholar] [CrossRef] [PubMed]
- Rascón, C.; Velasco, E.; Mederos, L.; Navascués, G. Phase diagrams of systems of particles interacting via repulsive potentials. J. Chem. Phys. 1997, 106, 6689–6697. [Google Scholar] [CrossRef]
- Schmitt, J.; Hajiw, S.; Lecchi, A.; Degrouard, J.; Salonen, A.; Impéror-Clerc, M.; Pansu, B. Formation of Superlattices of Gold Nanoparticles Using Ostwald Ripening in Emulsions: Transition from fcc to bcc Structure. J. Phys. Chem. B 2016, 120, 5759–5766. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Lin, S.T.; Goddard, W.A. Efficiency of various lattices from hard ball to soft ball: Theoretical study of thermodynamic properties of dendrimer liquid crystal from atomistic simulation. J. Am. Chem. Soc. 2004, 126, 1872–1885. [Google Scholar] [CrossRef] [PubMed]
- Imai, M.; Yoshida, I.; Iwaki, T.; Nakaya, K. Static and dynamic structures of spherical nonionic surfactant micelles during the disorder-order transition. J. Chem. Phys. 2005, 122, 044906. [Google Scholar] [CrossRef] [PubMed]
- Filion, L.; Marechal, M.; van Oorschot, B.; Pelt, D.; Smallenburg, F.; Dijkstra, M. Efficient method for predicting crystal structures at finite temperature: variable box shape simulations. Phys. Rev. Lett. 2009, 103, 188302. [Google Scholar] [CrossRef] [PubMed]
- De Graaf, J.; Filion, L.; Marechal, M.; van Roij, R.; Dijkstra, M. Crystal-structure prediction via the Floppy-Box Monte Carlo algorithm: Method and application to hard (non) convex particles. J. Chem. Phys. 2012, 137, 214101. [Google Scholar] [CrossRef] [PubMed]
- Bianchi, E.; Doppelbauer, G.; Filion, L.; Dijkstra, M.; Kahl, G. Predicting patchy particle crystals: Variable box shape simulations and evolutionary algorithms. J. Chem. Phys. 2012, 136, 214102. [Google Scholar] [CrossRef] [PubMed]
- Gottwald, D.; Kahl, G.; Likos, C.N. Predicting equilibrium structures in freezing processes. J. Chem. Phys. 2005, 122, 204503. [Google Scholar] [CrossRef] [PubMed]
- Stokes, H.T.; Hatch, D.M. FINDSYM: Program for identifying the space-group symmetry of a crystal. J. Appl. Crystallogr. 2005, 38, 237–238. [Google Scholar] [CrossRef]
- Prestipino, S.; Saija, F.; Malescio, G. The zero-temperature phase diagram of soft-repulsive particle fluids. Soft Matter 2009, 5, 2795–2803. [Google Scholar] [CrossRef]
- Lennard-Jones, J.; Devonshire, A. Critical phenomena in gases. I. Proc. R. Soc. A 1937, 163, 53–70. [Google Scholar] [CrossRef]
- Rycroft, C.H. Voro++: A three-dimensional Voronoi cell library in C+. Chaos 2009, 19, 041111. [Google Scholar] [CrossRef] [PubMed]
- Vega, C.; Monson, P.A. Solid-liquid equilibrium for quadrupolar molecules. Mol. Phys. 1995, 85, 413–421. [Google Scholar] [CrossRef]
- Cottin, X.; Monson, P.A. A cell theory for solid solutions: Application to hard sphere mixtures. J. Chem. Phys. 1993, 99, 8914–8921. [Google Scholar] [CrossRef]
- Frenkel, D.; Smit, B.; Tobochnik, J.; McKay, S.R.; Christian, W. Understanding molecular simulation. Comput. Phys. 1997, 11, 351–354. [Google Scholar] [CrossRef]
- Likos, C.N.; Hoffmann, N.; Jusufi, A.; Löwen, H. Interactions and phase behaviour of polyelectrolyte star solutions. J. Phys. Condens. Matter 2002, 15, S233. [Google Scholar] [CrossRef]
- Hoffmann, N.; Likos, C.N.; Löwen, H. Structure and phase behavior of polyelectrolyte star solutions. J. Chem. Phys. 2004, 121, 7009–7021. [Google Scholar] [CrossRef] [PubMed]
- Noya, E.G.; Vega, C.; de Miguel, E. Determination of the melting point of hard spheres from direct coexistence simulation methods. J. Chem. Phys. 2008, 128, 154507. [Google Scholar] [CrossRef] [PubMed]
- Pansu, B.; Sadoc, J.F. Metallurgy of soft spheres with hard core: From BCC to Frank-Kasper phases. arXiv, 2017; arXiv:1707.07897. [Google Scholar]
- Pattabhiraman, H.; Dijkstra, M. Periodic layers of a dodecagonal quasicrystal and a floating hexagonal crystal in sedimentation-diffusion equilibria of colloids. J. Chem. Phys. 2017, 147, 104902. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Liu, Y.J.; Lu, X.; Teng, J. Fabrication of well-ordered binary colloidal crystals with extended size ratios for broadband reflectance. ACS Appl. Mater. Interfaces 2014, 6, 10265–10273. [Google Scholar] [CrossRef] [PubMed]
- Cai, Z.; Xiong, Z.; Lu, X.; Teng, J. In situ gold-loaded titania photonic crystals with enhanced photocatalytic activity. J. Mater. Chem. A 2014, 2, 545–553. [Google Scholar] [CrossRef]
- Cheng, W.; Wang, J.; Jonas, U.; Fytas, G.; Stefanou, N. Observation and tuning of hypersonic bandgaps in colloidal crystals. Nat. Mater. 2006, 5, 830–836. [Google Scholar] [CrossRef] [PubMed]
- Baumgartl, J.; Zvyagolskaya, M.; Bechinger, C. Tailoring of phononic band structures in colloidal crystals. Phys. Rev. Lett. 2007, 99, 205503. [Google Scholar] [CrossRef] [PubMed]
- Van Blaaderen, A.; Ruel, R.; Wiltzius, P. Template-directed colloidal crystallization. Nature 1997, 385, 321. [Google Scholar] [CrossRef]
- Velikov, K.P.; Christova, C.G.; Dullens, R.P.A.; van Blaaderen, A. Layer-by-layer growth of binary colloidal crystals. Science 2002, 296, 106–109. [Google Scholar] [CrossRef] [PubMed]
- Bauer, J.L.; Kurian, M.J.; Stauffer, J.; Furst, E.M. Suppressing the Rayleigh–Plateau Instability in Field-Directed Colloidal Assembly. Langmuir 2016, 32, 6618–6623. [Google Scholar] [CrossRef] [PubMed]





© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gabriëlse, A.; Löwen, H.; Smallenburg, F. Low-Temperature Crystal Structures of the Hard Core Square Shoulder Model. Materials 2017, 10, 1280. https://doi.org/10.3390/ma10111280
Gabriëlse A, Löwen H, Smallenburg F. Low-Temperature Crystal Structures of the Hard Core Square Shoulder Model. Materials. 2017; 10(11):1280. https://doi.org/10.3390/ma10111280
Chicago/Turabian StyleGabriëlse, Alexander, Hartmut Löwen, and Frank Smallenburg. 2017. "Low-Temperature Crystal Structures of the Hard Core Square Shoulder Model" Materials 10, no. 11: 1280. https://doi.org/10.3390/ma10111280
APA StyleGabriëlse, A., Löwen, H., & Smallenburg, F. (2017). Low-Temperature Crystal Structures of the Hard Core Square Shoulder Model. Materials, 10(11), 1280. https://doi.org/10.3390/ma10111280