Revealing the Effect of Local Connectivity of Rigid Phases during Deformation at High Temperature of Cast AlSi12Cu4Ni(2,3)Mg Alloys
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Methods
2.3. Image Analysis
2.3.1. Pre-Processing
2.3.2. Image Segmentation
2.3.3. Characterization of the 3D Microstructure and Damage
3. Results
3.1. Influence of Chemical Composition on the Microstructure
Initial Microstructure
3.2. Tensile Tests at 300 °C
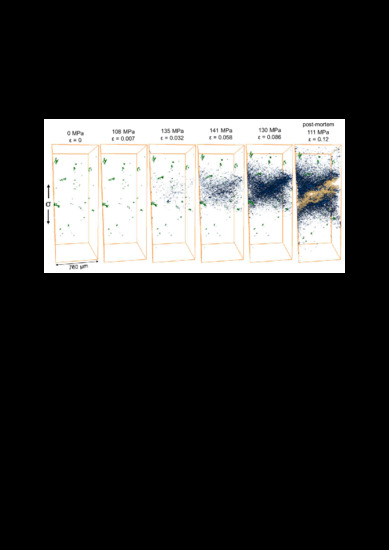
Damage Formation and Accumulation during Tensile Tests at 300 °C
4. Discussion
4.1. Influence of Chemical Composition on the Microstructure and Damage Evolution
- Formation of micro-cracks through primary Si particles agglomerated in clusters, voids at matrix/rigid phase interfaces as well as voids in the matrix can be seen in the early stages of damage. Fracture of isolated primary Si particles and eutectic Si can also occur if they are located in the vicinity of primary Si clusters. While the formation of voids in the matrix and at the interface between the matrix and the rigid phases was observed simultaneously with micro-cracking of primary Si in the AlSi12Cu4Ni2Mg alloy, these two mechanisms seem to occur at a later deformation stage for AlSi12Cu4Ni3Mg. Further sXCT scans at strains between 0.007 and 0.0032 are necessary for the AlSi12Cu4Ni2Mg alloy to fully clarify this difference.
- Coalescence of voids leading to final failure with the main crack propagating along damaged rigid particles as well as through the matrix.
4.2. Analytical Stress Partition Model to Gain Further Insights into the Mechanical Behavior of Al-Si Piston Alloys
5. Conclusions
- The additional formation of platelet-like Al-,Cu-,Ni-rich δ-phase owing to the increase of Ni content by 1 wt.% results in a larger amount of connecting branches and thus, a significant increase of local connectivity (quantified by the Euler number χ) of the rigid 3D network at practically constant global interconnectivity for the 3 wt.% Ni alloy.
- The in-situ tensile tests at 300 °C revealed ~10% higher strength and ~30% higher elongation at fracture of the 2 wt.% Ni alloy as compared to the 3 wt.% Ni alloy. Damage mechanisms during tensile deformation are the same for both alloys:
- ○
- Damage mainly initiates as micro-cracking through primary Si particles agglomerated in clusters, voids at matrix/rigid phase interfaces, as well as voids in the matrix. Moreover, isolated primary Si particles and eutectic Si can break if they are located close to clusters. Failure occurs by coalescence of voids with the main crack propagating along fractured rigid particles as well as through the α-Al-matrix.
- ○
- The lower local connectivity of the 3D network in AlSi12Cu4Ni2Mg permits local plastification of the matrix and helps accommodating more damage resulting in an increase of ductility with respect to AlSi12Cu4Ni3Mg. On the other hand, the 3 wt.% Ni alloy reveals damage onset at earlier deformation steps and less damage accumulation until failure compared to the 2% Ni alloy. The presence of more connecting branches in AlSi12Cu4Ni3Mg favors crack propagation through the rigid network and, consequently, final fracture occurs at lower strains with respect to the 2 wt.% Ni alloy.
- The evolution of local connectivity of the rigid 3D networks with damage accumulation based on experimental observations was implemented in a simple analytical stress partition model. The lower local connectivity at practically constant global interconnectivity of the 3D network in AlSi12Cu4Ni2Mg indicates two consequences:
- ○
- its lower rigidity allows local plastification and strain hardening of the α-Al matrix resulting in the higher strength of this alloy.
- ○
- more damage can be accommodated leading to higher elongation at fracture than for AlSi12Cu4Ni3Mg.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Asghar, Z.; Requena, G.; Boller, E. 3D rigid multiphase networks providing high-temperature strength to cast AlSi10Cu5Ni1-2 piston alloys. Acta Mater. 2011, 59, 6420–6432. [Google Scholar] [CrossRef] [PubMed]
- Requena, G.; Garcés, G.; Asghar, Z.; Marks, E.; Staron, P.; Cloetens, P. The Effect of Connectivity of Rigid Phases on Strength of Al-Si Alloys. Adv. Eng. Mater. 2011, 13, 674–684. [Google Scholar] [CrossRef]
- Mohamed, A.M.A.; Samuel, F.H. A Review on the Heat Treatment of Al-Si-Cu/Mg Casting Alloys. INTEC 2012. [Google Scholar] [CrossRef]
- Zhu, P.Y.; Liu, Q.Y.; Hou, T.X. Spheroidization of eutectic Silicon in Aluminum-Silicon Alloys. AFS Trans. 1985, 93, 609–614. [Google Scholar]
- Konečná, R.; Fintová, S.; Nicoletto, G.; Riva, E. High temperature fatigue strength and quantitative metallography of an eutectic Al-Si alloy for piston application. Key Eng. Mater. 2014, 592–593, 627–630. [Google Scholar] [CrossRef]
- Shabestari, S.G.; Moemeni, H. Effect of copper and solidification conditions on the microstructure and mechanical properties of Al-Si-Mg alloys. J. Mater. Process. Technol. 2004, 153–154, 193–198. [Google Scholar] [CrossRef]
- Efzan, M.N.E.; Kong, H.J.; Kok, C.K. Review: Effect of Alloying Element on Al-Si alloys. Adv. Mater. Res. 2014, 845, 355–359. [Google Scholar] [CrossRef]
- Jeong, C.-Y. Effect of Alloying elements on high temperature mechanical properties for piston alloy. Mater. Trans. 2012, 53, 234–239. [Google Scholar] [CrossRef]
- Zhang, W.D.; Yang, J.; Dang, J.Z.; Liu, Y.; Xu, H. Effects of Si, Cu and Mg on the high temperature mechanical properties of Al-Si-Cu-Mg alloy. Adv. Mater. Res. 2013, 652–654, 1030–1034. [Google Scholar] [CrossRef]
- Silva, F.S. Fatigue on engine pistons—A compendium of case studies. Eng. Fail. Anal. 2006, 13, 480–492. [Google Scholar] [CrossRef]
- Asghar, Z.; Requena, G.; Kubel, F. The role of Ni and Fe aluminides on the elevated temperature strength of an AlSi12 alloy. Mater. Sci. Eng. A 2010, 527, 5691–5698. [Google Scholar] [CrossRef]
- Asghar, Z.; Requena, G.; Degischer, H.P.; Cloetens, P. Three-dimensional study of Ni aluminides in an AlSi12 alloy by means of light optical and synchrotron microtomography. Acta Mater. 2009, 57, 4125–4132. [Google Scholar] [CrossRef]
- Requena, G.; Degischer, H.P. Three-Dimensional Architecture of Engineering Multiphase Metals. Ann. Rev. Mater. Res. 2012, 42, 145–161. [Google Scholar] [CrossRef]
- Asghar, Z.; Requena, G.; Zahid, G.H. Effect of thermally stable Cu- and Mg-rich aluminides on the high temperature strength of an AlSi12CuMgNi alloy. Mater. Charact. 2014, 88, 80–85. [Google Scholar] [CrossRef]
- Asghar, Z.; Requena, G.; Degischer, H.P.; Boller, E. Influence of Internal Architectures of Cast AlSi10Cu5Ni1-2 on High Temperature Strength. In Proceedings of the 12th International Conference on Aluminium Alloys, Yokohama, Japan, 5–9 September 2010; pp. 1285–1290. [Google Scholar]
- Bugelnig, K.; Sket, F.; Germann, H.; Steffens, T.; Koos, R.; Wilde, F.; Boller, E.; Requena, G. Influence of 3D connectivity of rigid phases on damage evolution during tensile deformation of an AlSi12Cu4Ni2 piston alloy. Mater. Sci. Eng. A 2018, 709, 193–202. [Google Scholar] [CrossRef]
- Kruglova, A.; Engstler, M.; Gaiselmann, G.; Stenzel, O.; Schmidt, V.; Roland, M.; Diebels, S.; Mücklich, F. 3D connectivity of eutectic Si as key property defining strength of Al-Si alloys. Comput. Mater. Sci. 2016, 120, 90–107. [Google Scholar] [CrossRef]
- Cho, Y.-H.; Im, Y.-R.; Kwon, S.-W.; Lee, H.C. The Effect of Alloying Elements on the Microstructure and Mechanical Properties of Al-12Si Cast Alloys. Mater. Sci. Forum 2003, 426–432, 339–344. [Google Scholar] [CrossRef]
- Stadler, F.; Antrekowitsch, H.; Fragner, W.; Kaufmann, H.; Uggowitzer, P.J. The effect of Ni on the high-temperature strength of Al-Si cast alloys. Mater. Sci. Forum 2011, 690, 274–277. [Google Scholar] [CrossRef]
- Konečná, R.; Nicoletto, G.; Kunz, L.; Svoboda, M.; Bača, A. Fatigue strength degradation of AlSi12cuNiMg alloy due to high temperature exposure: A structural investigation. Procedia Eng. 2014, 74, 43–46. [Google Scholar] [CrossRef]
- Li, Y.; Yang, Y.; Wu, Y.; Liu, X. Quantitative comparison of three Ni-containing phases to the elevated-temperature properties of Al–Si piston alloys. Mater. Sci. Eng. A 2010, 527, 7132–7137. [Google Scholar] [CrossRef]
- Toriwaki, J.; Yonekura, T. Euler Number and Connectivity Indexes of a Three Dimensional Digital Picture. Forma 2002, 17, 183–209. [Google Scholar]
- Aydogan, D.B.; Hyttinen, J. Characterization of microstructures using contour tree connectivity for fluid flow analysis. R. Soc. Interface 2014, 11. [Google Scholar] [CrossRef] [PubMed]
- Silva, M.J.; Gibson, L.J. The effect of non-periodic microstructure and defects on the compressive strength of two-dimensional cellular solids. Int. J. Mech. Sci. 1997, 39, 549–563. [Google Scholar] [CrossRef]
- ID19—Microtomography Beamline. Available online: http://www.esrf.eu/home/UsersAndScience/Experiments/StructMaterials/ID19.html (accessed on 5 July 2018).
- Schindelin, J.; Arganda-Carreras, I.; Frise, E. Fiji: An open-source platform for biological-image analysis. Nat. Methods 2012, 9, 676–682. [Google Scholar] [CrossRef] [PubMed]
- Requena, G.C.; Degischer, P.; Marks, E.D.; Boller, E. Microtomographic study of the evolution of microstructure during creep of an AlSiCuMgNi alloy reinforced with Al2O3 short fibres. Mater. Sci. Eng. A 2008, 487, 99–107. [Google Scholar] [CrossRef]
- Zeren, M. Effect of copper and silicon content on mechanical properties in Al-Cu-Si-Mg alloys. J. Mater. Process. Technol. 2005, 169, 292–298. [Google Scholar] [CrossRef]
- Belov, N.A.; Eskin, D.G.; Avxentieva, N.N. Constituent phase diagrams of the Al-Cu-Fe-Mg-Ni-Si system and their application to the analysis of aluminium piston alloys. Acta Mater. 2005, 53, 4709–4722. [Google Scholar] [CrossRef]
- Farkoosh, A.; Javidani, M.; Hoseini, M.; Larouche, D.; Pekguleryuz, M. Phase formation in as-solidified and heat-treated Al-Si-Cu-Mg-Ni alloys, Thermodynamic assessment and experimental investigation for alloy design. J. Alloy Compd. 2013, 551, 596–606. [Google Scholar] [CrossRef]
- Ceschini, L.; Boromei, I.; Morri, A.; Seifeddine, S.; Svensson, I.L. Microstructure, tensile and fatigue properties of the Al-10%Si-12%Cu alloy with different Fe and Mn content under controlled conditions. J. Mater. Process. Technol. 2009, 209, 5669–5679. [Google Scholar] [CrossRef]
- Zamani, M.; Seifeddine, S.; Jarfors, A.E.W. High Temperature tensile deformation and failure mechanisms of an Al-Si-Cu-Mg cast alloy—The microstructural scale effect. Mater. Des. 2015, 86, 361–370. [Google Scholar] [CrossRef]
- Su, J.F.; Nie, X.; Stoilov, V. Characterization of fracture and debonding of Si particles in AlSi Alloys. Mater. Sci. Eng. A 2010, 527, 7168–7175. [Google Scholar] [CrossRef]
- Lebyodkin, M.; Deschamps, A.; Bréchet, Y. Influence of second phase morphology and topology on mechanical and fracture properties of Al-Si alloys. Mater. Sci. Eng. A 1997, 234–236, 481–484. [Google Scholar] [CrossRef]
- Gall, K.; Horstemeyer, M.; McDowell, D.L.; Fan, J. Finite element analysis of the stress distributions near damaged Si particle clusters in cast Al-Si alloys. Mech. Mater. 2000, 32, 277–301. [Google Scholar] [CrossRef]
- Morgenstern, R.; Kenningley, S. Transient microstructural thermomechanical fatigue and deformation characteristics under superimposed mechanical and thermal loading, in AlSi based automotive diesel pistons. In Light Metals 2013; The Minerals, Metals & Materials Series; Sadler, B.A., Ed.; Springer: Cham, Switzerland, 2016; pp. 397–403. ISBN 978-3-319-65136-1. [Google Scholar]
- Mondolfo, L.F. Aluminium Alloys: Structure and Properties; Butterworth & Co. Ltd.: London, UK, 1976; ISBN 0408709324. [Google Scholar]
- Joyce, M.R.; Styles, C.M.; Reed, P.A.S. Elevated temperature short crack fatigue behaviour in near eutectic Al-Si alloys. Int. J. Fatigue 2003, 25, 863–869. [Google Scholar] [CrossRef]
- Zhang, G.; Zhang, J.; Li, B.; Cai, W. Characterization of tensile fracture in heavily alloyed Al-Si piston alloy, Progress in Natural Science. Mater. Int. 2011, 21, 380–385. [Google Scholar]
- Wang, M.; Pang, J.; Qiu, Y.; Liu, H.; Li, S.; Zhang, Z. Tensile Strength Evolution and Damage Mechanisms of Al–Si Piston Alloy at Different Temperatures. Adv. Eng. Mater. 2018, 20, 1700610. [Google Scholar] [CrossRef]
- Summers, P.T.; Chen, Y.; Rippe, C.M.; Allen, B.; Mouritz, A.P.; Case, S.W.; Lattimer, B.Y. Overview of aluminum alloy mechanical properties during and after fires. Fire Sci. Rev. 2015, 4, 3. [Google Scholar] [CrossRef]
- Chen, C.L.; Richter, A.; Thomson, R.C. Investigation of mechanical properties of intermetallic phases in multi-component Al-Si using hot-stage nanointendation. Intermetallics 2010, 18, 499–508. [Google Scholar] [CrossRef]













| Alloy | Al | Si | Cu | Ni | Mg |
|---|---|---|---|---|---|
| AlSi12Cu4Ni2Mg | bal. | 12.5 | 4 | 2 | 1 |
| AlSi12Cu4Ni3Mg | bal. | 13.1 | 4 | 3 | 1 |
| Experiment | Detector | Energy (keV) | FOV (mm2) | Sample to Detector Distance (mm) | Exposure Time (s/proj) | Proj. | Voxel Size (µm3) | Total Scan Time (s) |
|---|---|---|---|---|---|---|---|---|
| In-situ tensile tests at 300 °C | PCO Dimax | 19 | 1 × 2 | 150 | 0.01 | 1000 | 1.13 | 20 |
| Alloy | HB (1/10) | H (GPa) |
|---|---|---|
| AlSi12Cu4Ni2Mg | 126 ± 2.7 | 1.8 ± 0.1 |
| AlSi12Cu4Ni3Mg | 129 ± 1.4 | 1.8 ± 0.1 |
| Parameter | AlSi12Cu4Ni2Mg | AlSi12Cu4Ni3Mg |
|---|---|---|
| A1 | −822.5 | −2051.4 |
| A2 | −420.2 | −1886.5 |
| p | 3.6 | 1.9 |
| x0 | 0.047 | 0.023 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bugelnig, K.; Germann, H.; Steffens, T.; Sket, F.; Adrien, J.; Maire, E.; Boller, E.; Requena, G. Revealing the Effect of Local Connectivity of Rigid Phases during Deformation at High Temperature of Cast AlSi12Cu4Ni(2,3)Mg Alloys. Materials 2018, 11, 1300. https://doi.org/10.3390/ma11081300
Bugelnig K, Germann H, Steffens T, Sket F, Adrien J, Maire E, Boller E, Requena G. Revealing the Effect of Local Connectivity of Rigid Phases during Deformation at High Temperature of Cast AlSi12Cu4Ni(2,3)Mg Alloys. Materials. 2018; 11(8):1300. https://doi.org/10.3390/ma11081300
Chicago/Turabian StyleBugelnig, Katrin, Holger Germann, Thomas Steffens, Federico Sket, Jérôme Adrien, Eric Maire, Elodie Boller, and Guillermo Requena. 2018. "Revealing the Effect of Local Connectivity of Rigid Phases during Deformation at High Temperature of Cast AlSi12Cu4Ni(2,3)Mg Alloys" Materials 11, no. 8: 1300. https://doi.org/10.3390/ma11081300
APA StyleBugelnig, K., Germann, H., Steffens, T., Sket, F., Adrien, J., Maire, E., Boller, E., & Requena, G. (2018). Revealing the Effect of Local Connectivity of Rigid Phases during Deformation at High Temperature of Cast AlSi12Cu4Ni(2,3)Mg Alloys. Materials, 11(8), 1300. https://doi.org/10.3390/ma11081300