Non-Destructive Testing of a Sport Tribune under Synchronized Crowd-Induced Excitation Using Vibration Analysis
Abstract
:1. Introduction
2. Theoretical Background of the Experimental Modal Analysis
3. Experimental Dynamic Identification of the Grandstand
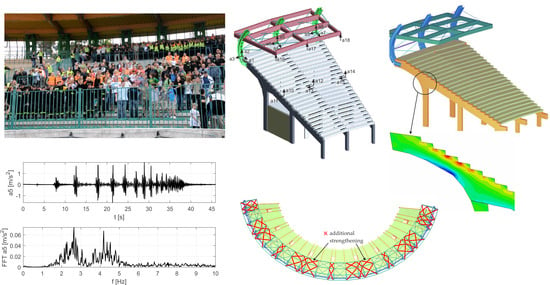
3.1. Description of the Structure
3.2. Test Procedure and Vibration Measurement
4. Finite Element Method Modeling
4.1. Identification of the Jump Load Function
4.2. Numerical Analysis
5. Structural Tuning
6. Conclusions
- (1)
- The key natural vibration frequency of 4.68 Hz coincided with the frequency of the higher harmonics of the excitation force (approximately 4.4 Hz).
- (2)
- The reinforced concrete cross-section of the BR2 main girder was scratched. The calculated decrease in the stiffness after scratching was equal to about 50%. The inclusion of scratches reduced the calculated initial natural vibration frequencies of the structure by 5%–10% in comparison with the unscratched cross-section.
- (3)
- The dynamic and synchronic nature of the Labado dance is accidental, but can constitute vandalism. Fans jumping to the rhythm of the animator's regular drumming results in increasing stand vibrations, causing the serviceability limit state to be exceeded. The stand vibrations can lead to material fatigue and, as a result, to its complete destruction.
- (4)
- The proposal to solve the problem of overlapping frequencies causing resonance by changing the animator's drumming rhythm and using it for the needs of dynamic impact elimination in favor of the static impact of people on the stand structure was not accepted by club authorities nor by fans. This objection was explained by the long-term Ladabo dance tradition at the Swiss Krono Arena stadium. Any changes in the drumming rhythm would result in the loss of the cheering spirit among fans used to dancing the Labado.
- (5)
- The proposed original concept of stadium structural tuning significantly reduced the amplitude of the stand structure vibrations. Individual resonance zones were moved towards higher frequencies after tuning, which allowed for safe use of the stadium.
- (6)
- There is a high probability of the occurrence of double natural vibrations frequencies or frequencies with close values in the case of spatial constructions with large dimensions and repeated construction segments. Therein, the phenomenon of the beat will appear, which may cause an increase in tribune elements displacement. The post-tuning FEM model of a structure does not indicate the occurrence of such a case. However, if the actual post-tuning stand structure had double frequencies in a range of up to 5 Hz, additional structure strengthening might be necessary.
- (7)
- The implementation of the architectural structure form resulted in a static scheme in which a roof structure cantilever steel column was mounted at the end of the stand’s reinforced concrete cantilever. The girders working as cantilevers were fixed at the cantilever steel column end. This results in fragility under dynamic load applied to the cantilever part of the concrete beams. Sports facilities must ensure the freedom of supporters gathered in the stands and all possible dances and ways to cheer their favorite teams must be included in the design and implementation process.
- (8)
- The non-destructive tests and numerical simulations conducted in this paper are innovative and pioneering. Currently, no standard has been developed that allows for the determination of performance conditions and methods for testing the resistance of stadium stands to jump loads. The normative documents also lack a ready-to-use jump load function that could be used when designing a structure.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Melrose, A.; Hampton, P.; Manu, P. Safety at sports stadia. Procedia Eng. 2011, 14, 2205–2211. [Google Scholar] [CrossRef]
- Soomaroo, L.; Murray, V. Disasters at Mass Gatherings: Lessons from History. PLOS Curr. Disasters 2012. [Google Scholar] [CrossRef] [PubMed]
- Proença, J.M.; Branco, F. Case studies of vibrations in structures. Rev. Eur. génie Civ. 2007, 9, 159–186. [Google Scholar] [CrossRef]
- Sachse, R.; Pavic, A.; Reynolds, P. Parametric study of modal properties of damped two-degree-of-freedom crowd–structure dynamic systems. J. Sound Vib. 2004, 274, 461–480. [Google Scholar] [CrossRef]
- Reynolds, P.; Pavic, A. Vibration Performance of a Large Cantilever Grandstand during an International Football Match. J. Perform. Constr. Facil. 2006, 20, 202–212. [Google Scholar] [CrossRef]
- Yang, Y. Comparison of bouncing loads provided by three different human structure interaction models. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering, Wuhan, China, 26–28 June 2010; pp. 804–807. [Google Scholar]
- Bachmann, H. Case Studies of Structures with Man-Induced Vibrations. J. Struct. Eng. 1992, 118, 631–647. [Google Scholar] [CrossRef]
- Santos, F.; Cismaşiu, C.; Cismaşiu, I.; Bedon, C. Dynamic Characterisation and Finite Element Updating of a RC Stadium Grandstand. Building 2018, 8, 141. [Google Scholar] [CrossRef]
- Jones, C.; Reynolds, P.; Pavic, A. Vibration serviceability of stadia structures subjected to dynamic crowd loads: A literature review. J. Sound Vib. 2011, 330, 1531–1566. [Google Scholar] [CrossRef]
- Gul, M.; Catbas, F.N. A Review of Structural Health Monitoring of a Football Stadium for Human Comfort and Structural Performance. Struct. Congr 2013, 2445–2454. [Google Scholar]
- Ren, L.; Yuan, C.-L.; Li, H.-N.; Yi, T.-H. Structural Health Monitoring System Developed for Dalian Stadium. Int. J. Struct. Stab. Dyn. 2015, 16, 1640018. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Manzato, S.; Peeters, B.; Marulo, F.; Desmet, W. Structural Health Monitoring strategies based on the estimation of modal parameters. Procedia Eng. 2017, 199, 3182–3187. [Google Scholar] [CrossRef]
- Spencer, B.F.; Ruiz-Sandoval, M.E.; Kurata, N.; Ruiz-Sandoval, M.E. Smart sensing technology: opportunities and challenges. Struct. Control. Heal. Monit. 2004, 11, 349–368. [Google Scholar] [CrossRef]
- Bedon, C.; Bergamo, E.; Izzi, M.; Noè, S. Prototyping and Validation of MEMS Accelerometers for Structural Health Monitoring—The Case Study of the Pietratagliata Cable-Stayed Bridge. J. Sens. Actuator Networks 2018, 7, 30. [Google Scholar] [CrossRef]
- Hoła, J.; Bień, J.; Sadowski, Ł.; Schabowicz, K. Non-destructive and semi-destructive diagnostics of concrete structures in assessment of their durability. Bull. Pol. Acad. Sci. Tech. Sci. 2015, 63, 87–96. [Google Scholar] [CrossRef]
- Brandt, A. A signal processing framework for operational modal analysis in time and frequency domain. Mech. Syst. Signal Process. 2019, 115, 380–393. [Google Scholar] [CrossRef]
- Chen, G.-W.; Omenzetter, P.; Beskhyroun, S. Operational modal analysis of an eleven-span concrete bridge subjected to weak ambient excitations. Eng. Struct. 2017, 151, 839–860. [Google Scholar] [CrossRef]
- Torres, W.; Almazán, J.L.; Sandoval, C.; Boroschek, R. Operational modal analysis and FE model updating of the Metropolitan Cathedral of Santiago, Chile. Eng. Struct. 2017, 143, 169–188. [Google Scholar] [CrossRef]
- Idehara, S.J.; Júnior, M.D. Modal analysis of structures under non-stationary excitation. Eng. Struct. 2015, 99, 56–62. [Google Scholar] [CrossRef]
- Jannifar, A.; Zubir, M.; Kazi, S. Development of a new driving impact system to be used in experimental modal analysis (EMA) under operational condition. Sens. Actuators A Phys. 2017, 263, 398–414. [Google Scholar] [CrossRef]
- Prashant, S.W.; Chougule, V.; Mitra, A.C. Investigation on Modal Parameters of Rectangular Cantilever Beam Using Experimental Modal Analysis. Mater. Today Proc. 2015, 2, 2121–2130. [Google Scholar] [CrossRef]
- Hu, S.-L.J.; Yang, W.-L.; Liu, F.-S.; Li, H.-J. Fundamental comparison of time-domain experimental modal analysis methods based on high- and first-order matrix models. J. Sound Vib. 2014, 333, 6869–6884. [Google Scholar] [CrossRef]
- Clemente, P.; Marulo, F.; Lecce, L.; Bifulco, A. Experimental modal analysis of the Garigliano cable-stayed bridge. Soil Dyn. Earthq. Eng. 1998, 17, 485–493. [Google Scholar] [CrossRef]
- Lin, R. Identification of modal parameters of unmeasured modes using multiple FRF modal analysis method. Mech. Syst. Signal Process. 2011, 25, 151–162. [Google Scholar] [CrossRef]
- Rucka, M.; Wilde, K. Application of continuous wavelet transform in vibration based damage detection method for beams and plates. J. Sound Vib. 2006, 297, 536–550. [Google Scholar] [CrossRef]
- Chroscielewski, J.; Miśkiewicz, M.; Pyrzowski, Ł.; Rucka, M.; Sobczyk, B.; Wilde, K. Modal properties identification of a novel sandwich footbridge—Comparison of measured dynamic response and FEA. Compos. Part B Eng. 2018, 151, 245–255. [Google Scholar] [CrossRef]
- EN C. 1-1: Eurocode 1: Actions on Structures–Part 1-1: General Actions–Densities, Self-Weight, Imposed Loads for Buildings; European Committee for Standardization: Brussels, Belgium, 2002. [Google Scholar]





























© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grębowski, K.; Rucka, M.; Wilde, K. Non-Destructive Testing of a Sport Tribune under Synchronized Crowd-Induced Excitation Using Vibration Analysis. Materials 2019, 12, 2148. https://doi.org/10.3390/ma12132148
Grębowski K, Rucka M, Wilde K. Non-Destructive Testing of a Sport Tribune under Synchronized Crowd-Induced Excitation Using Vibration Analysis. Materials. 2019; 12(13):2148. https://doi.org/10.3390/ma12132148
Chicago/Turabian StyleGrębowski, Karol, Magdalena Rucka, and Krzysztof Wilde. 2019. "Non-Destructive Testing of a Sport Tribune under Synchronized Crowd-Induced Excitation Using Vibration Analysis" Materials 12, no. 13: 2148. https://doi.org/10.3390/ma12132148
APA StyleGrębowski, K., Rucka, M., & Wilde, K. (2019). Non-Destructive Testing of a Sport Tribune under Synchronized Crowd-Induced Excitation Using Vibration Analysis. Materials, 12(13), 2148. https://doi.org/10.3390/ma12132148