4.1. Observations of the Compressing Network: Stress–strain Behavior and Image Analysis
There are several possible measurement techniques to test compression properties of single fibers [
28]. However, in practice it is difficult to pinpoint the initiation of a buckling failure and separate this from normal bending [
28]. In the current work, the deformation of fibers and fiber segments inside highly porous compressed materials was observed with high-speed imaging and related correlation analysis. The aim was to see how heterogeneous the overall compression behavior was and to characterize some relevant deformation modes. In particular, we recorded abrupt dislocations of fiber segments inside the material network. Observed fiber bending generally led to smoother and slower deformations than these dislocations, which we interpreted as segment bucklings.
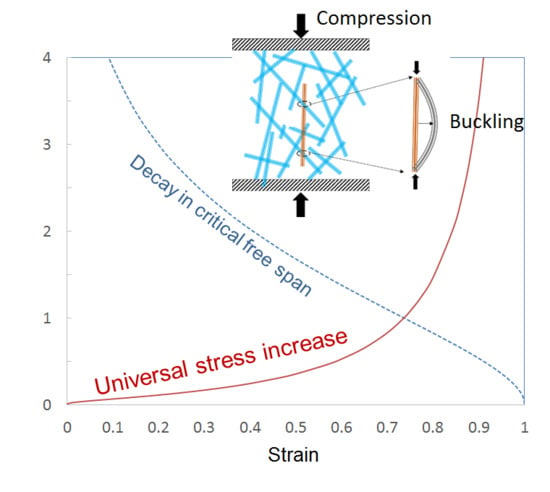
Figure 4 shows cyclic stress–strain curves for samples made of Kraft and CTMP fibers and having similar density. CTMP samples exhibited higher tensile strength and Young’s modulus due to the stiff but still well-bonding chemi-thermomechanical pulp fibers. Both curve sets show strain stiffening, which is typical for all fiber networks [
14] and is described by the theoretical analysis of
Section 3 based on the free-span length distribution. In particular, formation of new interfiber contacts is not required to explain strain stiffening, which contradicts a conclusion of Alimadadi et al. [
19]. Moreover, the predicted stress increase with compression strain (see Equation (8)) is followed well in both cases. In fact, we compared the stress at 50% compression to that at 10% compression for a set of 57 CTMP and Kraft trial points (see
Table 1) and obtained a mean ratio of 5.42 ± 0.43 (95% confidence interval) for the relative stresses over this data set. This value is well in accordance with the theoretically predicted ratio 5.374, which indicates almost perfect average agreement with our postulate on the dominance of the buckling mechanism. As the theory predicts universality along the whole compression curve, similar comparison of relative stresses could have been carried out for any other strain levels. Here we picked up the most typical ones.
The standard deviation of the average
ratio over the 57 trial points was 1.60 with the distribution shown in
Figure 5. A significant proportion of the data points are centered in close vicinity of the universal mean value. However, there are a few cases with larger deviation from this value. There can be several reasons for the variation of the stress–compression behavior between individual trial points or samples. For example, in addition to increasing density and shortening of the free-span fiber segments, a more even distribution of the stress over the whole fiber material could also contribute to this behavior [
21]. One would expect local compressions to first concentrate in the material regions that are more open than the average material structure. The foam forming process generates a much wider pore size (and thus free-span distribution) in the CTMP fiber network than in the network consisting of BSKP fibers [
23]. This leads to a highly nonlinear stress–strain curve, as shown in
Figure 4. The theoretical prediction of Equation (8) follows the experimental curves rather well in both cases, except at small compressive strains under 10%. For the model curves in
Figure 4, the constant factor appearing in Equation (8) was not fitted at
(the measured curves did not extend that far) but at 15% compression, so that the model agreed with the central parallel measurement. The deviation at small strains could come, e.g., from fiber bending appearing at sample surfaces (also affecting the origin of the strain axis), or other factors not included in our theory.
The behavior of a CTMP network along a 50% compression cycle is presented in
Figure 6. The duration of the compression part is 27.3 s, and it is represented with 264 image frames. As the image acquisition was manually triggered, it was slightly delayed from the actual start of the compression. The sample was standing on a plate, and the camera was directed to its outer surface directly above the plate. Because of the very open porous structure, most of the imaged fibers were located inside the material rather than at the immediate outer surface. As an overview, the deformation appeared to be affine [
14] and smooth, without major events. During compression of the fiber network, distinctive events of any type appeared at first to be rather rare by simple visual inspection. However, the volume of the region that was followed was rather small. The x−y window size was 6.7 mm × 5.4 mm, whereas in the depth direction, the focus length was clearly below 1 mm. For affine deformation, the vertical movement of a fiber segment in the upper part of this window within one frame was expected to be 0.5 × 5.4/264 mm = 10 µm, i.e., less than the fiber radius. Occasionally, a section of an individual fiber was abruptly dislocated much more within one frame (i.e., during 100 ms). Within the studied small region, eleven of such events were easily pinpointed at compression levels of 14.4%, 17.8%, 31.4%, 37.5%, 38.3%, 38.8%, 39.0%, 40.0%, 41.1%, 43.9%, and 44.1%. Typically one to four fibers participated in these events. Only at the very end of the cycle, e.g., at 39.4% and 47.3%, could significant bending or bulging of individual fibers be observed.
The obtained images were analyzed further using the image correlation technique. By calculation of local cross-correlation at each position in two subsequent images, movements of fibers can be detected in the whole image area. In this way, many more fiber dislocations could be observed than those events listed above, see
Figure 6. In addition to the above large dislocations, the image correlation technique revealed similar smaller events in most of the studied frames. Typically, one or a few fibers had significant abrupt movement between subsequent frames (differentiated as a color change), whereas the behavior was smooth for the rest of the fiber network. The smooth behavior was indicated by the orange color corresponding to well correlating subsequent frames at the corresponding location of the network. Similar dislocations were found in all fiber orientations. There were a few frames in which practically the whole studied region was still (shown as an orange region in the correlation plots), and in some frames a number of fibers appeared to be moving suddenly. However, it was easiest to observe dislocations near the bottom region, where the colored fibers were located. Interestingly, practically no similar dislocations were observed when letting the network relax by moving out the external load after the peak point of
Figure 6a.
Figure 7 shows cyclic stress–strain curves for viscose samples V6 and V9. The stress–compression behavior is again followed well, especially at the lower CNF-content, for which the basic assumptions of the theory on the role of the free-span lengths are likely to be valid. As shown in
Figure 7a, the 2nd cycle produces a lower stress than the 1st cycle due to the buckled segments until the maximal strain of the 1st cycle is achieved. Beyond this 50% strain level, new segment bucklings are required so that the stress rises and continues the trend set by the 1st cycle. The formed envelope of the two cycles is nicely predicted by the theory of
Section 3. The higher CNF-content in Sample V9 leads to greater stress already at intermediate strain levels in
Figure 7b. This suggests that the interfiber contacts created by nanocellulose are rather stiff and do not break appreciably in this sample. Moreover, it is probable that nanocellulose forms small membranes with their own substructure inside the fiber network at the high CNF content [
29].
Figure 8 and
Figure 9 show the 50% compression cycle for viscose sample V6, with a CNF-content of 1.0, and for V9, with a CNF-content of 5.0, together with snapshots of the network from the compression part. The high amount of CNF can be seen in the images of V9 as dark spots.
Deformations of low-density random fiber networks have been shown to be non-affine [
14]. This means that local deformation fields fluctuate around an average expansion or compression behavior. With decreasing density, non-affine deformation tendency becomes more noticeable. During testing of the thick (or high) viscose fiber samples, we also observed rather large deformation fronts on the sample surface. Similar uneven progression of the compression was observed in the videos. For example, the region in the upper right corner of V6 was compressing faster at the average 30% to 50% compression levels than the other areas in the image.
Abrupt and countable dislocations of fibers occurring in 100 ms, i.e., between two consecutive frames were first visually counted from the recorded image sequences for samples V6 and V9. For V6 (see
Figure 8), dislocations of fibers, fiber groups, or fiber sections were easily seen at 4.3%, 7.5%, 17.5%, 18.0%, 19.3%, 30.4%, 31.3%, 37.3%, 38.2%, 38.4%, and 40.0% displacements. The correlation plots show many more dislocations of fibers. The dislocation activity in the network is high at low 5.6% compression, see
Figure 8c. This agrees with the earlier claims on the dominance of buckling failures at low compression levels. However, bucklings are frequent throughout the increasing compression cycle. For example, an abrupt strong fiber dislocation was observed at 17.9% compression (
Figure 8d), together with several smaller fiber movements at the same time. On the other hand, all fibers stayed still or moved smoothly occasionally, see
Figure 8e (41.8% compression). For the sample V6, the dislocations were rather evenly distributed over the whole studied region.
Figure 8f shows an example in which the dislocations concentrate on an upper part at 49.6% compression.
With increasing CNF content, the network becomes more connected and the response more collective, as shown in
Figure 9 for sample V9. However, it should be noted that often some fibers move much more than others for certain frames (e.g., see
Figure 9c,f). Despite the high dislocation activity throughout the increasing compression cycle, rather high maximum stress was still achieved (see
Figure 7b). The high connectivity means that a large population of all fibers contributes to load bearing, which improves the material strength.
4.2. Regression Model for Bonding Fibers
Mechanical CTMP pulp contains fibers with a wide length distribution as well as fines. The surface of the wood fibers is fibrillated due to the mechanical forces of the pulping process. In addition, CTMP fibers have different cellulose crystal structure and bending stiffness compared to regenerated cellulose fibers [
25]. Both fiber types are hydrophilic, but their bonding properties differ considerably. Whereas the CTMP fibers and wood fines bond strongly via hydrogen bonding and other short-range forces, viscose fibers have low bonding ability. On the other hand, strong-bonding Kraft fibers are more flexible than CTMP fibers and affect the mechanical properties of the Kraft fiber networks.
The speed and duration of mixing and the various geometries of the mixer setup, such as propeller shape, all have an effect on the obtained foam. For the wood fiber series, only the mixing time varied considerably. The target air content was between 50% and 60%. Especially for samples foamed with PVA, this level was not reached, and the air content remained at a lower level ranging from 40% to 50%.
The sample preparation was aimed at given densities (40 kg/m3, 60 kg/m3, and 80 kg/m3) and constant grammages (600 gsm, 800 gsm, 1200 gsm, and 1600 gsm). The 40 kg/m3 sample set contained the refined Kraft pulp raw materials. The sample thickness after oven drying (i.e., before compression) was clearly affected by surfactant type, and by pulp consistency in the mixing vessel. The smaller the consistency was, the easier it was to foam up the stock volume (leading to higher air content), and the higher was the resulting sample thickness after oven drying. The greatest drop in thickness was experienced between consistencies 1% and 2% for the unrefined BSKP0 samples. Almost invariably, SDS gave the highest thicknesses, followed by Tween and PVA. The distances that the samples had to be compressed to reach the 20 mm target thickness ranged from 70 mm, especially for samples prepared with SDS, to only 2.5 mm. The average final density and standard deviation for the samples (39 pcs) that targeted at 40 kg/m3 was 44.2 ± 4.2 kg/m3, for the 60 kg/m3 samples (12 pcs) 66.2 ± 5.6 kg/m3, and for the 80 kg/m3 samples (6 pcs) 84.1 ± 11.0 kg/m3.
Figure 10 shows the stresses at the 50% compression level. Equation (9) predicts a square dependence of the stress on the initial density at any strain level. Motivated by this fact, we plotted stress against the initial density and fitted power curves to the results for each surfactant separately (
Figure 10). All the data points appeared to follow their corresponding curves relatively closely. The density dependence was described with a power varying between 1.99 and 2.48 for the studied cases. The fact that the powers were rather close to 2 further supports the assumption that buckling is a dominant deformation mode underlying network strength, rather than fiber bending (corresponding to cubic dependence on density). The slight deviations from the square behavior could result from collective phenomena, such as distribution of bond properties that are not described by the idealized average model. The regression model predictions compared to the measured values are shown in
Figure 11. The residuals were relatively random, confirming the good fit of the regression models. However, the predictions appeared to be somewhat poorer at low stress values.
The stress levels were generally higher for CTMP compared to BSKP0. These fibers differ mainly in coarseness and openness of lumen. The difference in bending stiffness for the CTMP and Kraft fibers is described by the factor
EI in Equation (9). This factor is expected to be significantly higher for CTMP than for Kraft [
30]. On the other hand, a given density corresponds to a higher number of Kraft than CTMP fibers because of the lower coarseness (typically 0.14−0.18 mg/m [
31,
32]) of Kraft. It is difficult to sum up these factors into a reliable strength estimate, as precise values of the various parameters are not known. However, with the factor 1.5 difference in coarseness, together with a factor-of-three difference in dry bending stiffness (for wet fibers this difference would be larger [
30] because of higher moisture content in Kraft), Equation (9) predicts a similar difference in compression strength to that seen in
Figure 10.
General fibrous materials exhibit rigidity percolation, a critical density at which the structure acquires stiffness [
3,
14]. The threshold density is affected by, e.g., the nature of the fiber-to-fiber contacts, fiber orientation, and fiber bending stiffness. Below this density, Young’s and shear moduli are both considered to be zero. For low-density 3D wood–fiber networks, Burke et al. [
3] recently found the critical density to vary linearly with respect to the initial liquid fraction of foam used to form the structure. The obtained values varied in the range of 3 to 8 kg/m
3. Looking at their data (Figures 7 and 8 of Burke et al. [
3]), our theoretical model (Equation (8)) appears also to describe their stress–strain behavior reasonably well at 15 kg/m
3. The same holds at high strains for the case studied by Alimadadi and Uesaka ([
1], Figure 11a; see also Figure 15 of Alimadadi et al. [
19]) at as low a material density as 5 kg/m
3. On the other hand, the current theory does not explain the linear dependence of the compressive modulus on density observed by Burke et al. [
3], because the modulus was determined at very low strains beyond the validity of our model.
The regression models for unrefined BSKP0 samples were also applied to the refined samples (
Figure 12). Refining imparts damage, such as kinks, compressions, and delamination to fiber walls, and thus improves the bonding capacity of wood fibers. The effect can be seen as increasing compression stress, irrespective of the surfactant. The model fitted to the BSKP0 data could not capture this effect, and the estimation started to lag behind the measurements for BSKP1 and BSKP2. According to Rusu et al. [
33], the main contributing factor to fiber (FiberMaster) bendability is internal fibrillation rather than cross-sectional geometry (or moment of inertia). Internal fibrillation reduces the bending stiffness of a fiber wall, causes fiber collapse, and thus changes the boundary conditions in Equation (9).
4.3. Regression Model for Nonbonding Fibers
Regenerated viscose fibers from cellulose have considerably different structure and properties compared to natural wood fibers. Viscose fibers are manufactured as a single straight filament and are cut to length, generally leading to a smooth surface and uniform internal structure and cross-section. The viscose fibers show practically no bonding due to the very small contact area between their rounded surfaces. External bonding material, such as nanocellulose, is needed for the fiber assembly to maintain its integrity. By varying the absolute and relative amounts of binding material, the effects of fiber contact number and strength can be studied.
The preparation of the nonbonding viscose material did not aim at a predetermined density. Therefore, the sample densities ranged from 20 kg/m
3 to 80 kg/m
3 (see
Figure 13). In certain conditions, such as a certain raw material consistency range, the air content of the batch can be independently chosen as an endpoint for the mixing (foaming). In higher consistencies, foaming does not occur unless additional energy is introduced to the stock, or mixing duration is increased. For viscose samples, the consistencies were an order of magnitude higher compared to the wood fiber samples. Samples V4, V5, V8, and V9 were relatively hard and not easily pliable to compression. The lightest samples were very open arrays of fibers, and the least bound samples, particularly samples V6 and V7, easily disintegrated during handling.
Figure 14 summarizes the compression test results. The stresses increased as a function of density for both the constant and the varying CNF ratio series. It was not possible to compress samples V5 and V9 to 70% with the 1 kN load cell that was used.
The stresses at 50% compression were then plotted against the initial density, and a regression model was fitted to the data (see
Figure 15). It is evident that the behavior is different for the two series. The samples with constant CNF ratio had an increasing number of fiber contacts that were reinforced with equal shares of CNF fibers. In the regression model, the power exponent 2.58 was comparable to that for the wood fiber series, indicating a similar deformation mechanism to that described earlier in
Section 3. However, for the series with an increasing CNF ratio, both the number of fiber contacts and the relative amount of CNF reinforcing the contacts were increasing. The exponent 4.33 was considerably higher than for wood fiber samples. The difference reflects the potential of nanocellulose to form strong substructures in addition to strengthening the interfiber bonds. With increasing CNF concentration, a greater proportion of CNF forms membranes with a thickness of typically a couple of micrometers [
29]. These give additional strength to the material, which is not described by our buckling model.
The quality of the prediction obtained with regression curves is described by a residual plot shown in
Figure 16. Especially at lower stresses, the residuals are much higher than for the bonding fiber cases.