Next Article in Journal
Bactericidal and Biocompatible Properties of Plasma Chemical Oxidized Titanium (TiOB®) with Antimicrobial Surface Functionalization
Next Article in Special Issue
Effect of Nanodiamond Concentration and the Current Density of the Electrolyte on the Texture and Mechanical Properties of Ni/Nanodiamond Composite Coatings Produced by Electrodeposition
Previous Article in Journal
Microstructure and Mechanical Performance of Additively Manufactured Aluminum 2024-T3/Acrylonitrile Butadiene Styrene Hybrid Joints Using an AddJoining Technique
Previous Article in Special Issue
Tribological Performance of Nanocomposite Carbon Lubricant Additive
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Materials
Volume 12
Issue 6
10.3390/ma12060865
materials-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Effect by Diamond Surface Modification on Biomolecular Adhesion

by
Yuan Tian
and
Karin Larsson
*
Department of Chemistry—Ångström Laboratory, Uppsala University, BOX 538, 75121 Uppsala, Sweden
*
Author to whom correspondence should be addressed.
Materials 2019, 12(6), 865; https://doi.org/10.3390/ma12060865
Submission received: 16 January 2019 / Revised: 6 March 2019 / Accepted: 11 March 2019 / Published: 15 March 2019
(This article belongs to the Special Issue Nanodiamond Particles: Properties and Applications)
Browse Figures
Review Reports Versions Notes

Abstract

:
Diamond, as material, show very attractive properties. They include superior electronic properties (when doped), chemical inertness, controllable surface termination, and biocompatibility. It is thus clear that surface termination is very important for those applications where the implant material is based on diamond. The present theoretical work has focused on the effect of diamond surface termination, in combination with type of surface plane, on the adhesion of important biomolecules for vascularization and bone regeneration. These biomolecules include Arginine-Glycine-Aspartic acid (RGD), Chitosan, Heparin, Bone Morphogenetic Protein 2 (BMP2), Angiopoietin 1 (AGP1), Fibronectin and Vascular Endothelial Growth Factor (VEGF). The various surface planes are diamond diamond (100)-2x1 and (111). The theoretical results show that the non-covalent binding of these biomolecules is in proportion with their molecular weights. Moreover, three groups of biomolecules were observed for both types of surface planes. The most strongly binding biomolecule was the BMP2 molecule. The smaller polypeptides (RGD, Chitosan and Heparin) formed a less strongly binding group. Finally, the biomolecules VEGF, Fibronectin and Angiopoietin showed bond strengths numerically in between the other two groups (thereby forming a third group). Moreover, the (111) surface was generally observed to display a stronger bonding of the biomolecules, as compared with the (100)-2x1 surface.

Graphical Abstract

1. Introduction

Diamond is a material with very attractive properties. These include superior electronic properties (when doped), controllable surface termination, chemical inertness, high degree of biocompatibility, high transparency and a large electrochemical potential window, etc. When considering the well-known combination of chemical inertness, high transparency and high large electrochemical potential window [1,2], diamond became recently a promising candidate for applications like artificial photosynthetic water-splitting [3,4]. In addition, it has been observed that, because of the intrinsic biocompatibility and chemical stability, diamond can increase the duration of bone implants. Diamond will thereby become a preferred material for also biochemical applications [5,6].
Nano-crystalline diamond, or diamond material constructed from diamond nanoparticles with dimensions larger than ~3 nm in diameter, are today used for biochemical applications. The reactivity of these material surfaces is will depend on various factors: (i) diamond plane, (ii) surface termination and (iii) diamond particle size. It has both experimentally and theoretically been shown, that there is no size confinement for diamond particle diameters larger than ~2 nm [7,8]. In this work, it has therefore been assumed that nano-crystalline diamond or diamond particles of experimental sizes can be modelled using periodic supercells including the diamond low index planes (111) and (100)-2x1, respectively. The latter plane is a 2x1-reconstructed (100) surface.
A well-controlled surface termination with various species has not only proven to uphold the cubic structure of diamond, but also to change the reactivity and properties of the diamond surface region. For instance, specific surface termination can induce surface electronic conductivity and interfacial charge transfer properties. Other examples of properties that might be effected by surface termination are field emission characteristics [9], broad-band infrared reflectivity [10], hydrophilicity [11], electron conductivity [12] and electron affinity [13]. All these interesting properties make it clear that diamond surface termination is very important for especially those applications in which diamond can function as an electrode material [14].
Avascular necrosis causes cell death in various bone components. It is then common to replace the whole joints by artificial materials. However, the stability of these bone implant durations are not sufficiently high [15], so there is an urgent need to develop new biomaterials with increasing stability and biocompatibility. The biomaterials used today are hydroxyapatite, noble metals and polypropylenefumarate/polypropylenefumarate-diacrylate (PPF/PPF-DA). Hydroxyapatite may increase the biocompatibility, but does not show a good duration [16]. There are reports about resistant bacteria for noble metals, which have stopped its further use in the field [17]. Furthermore, local inflammations are a severe problem for the usage of PPF/PPF-DA implant materials [18]. However, diamond has proven to be an ideal biomaterial candidate for e.g., bone implants.
When developing new bone implant materials, a controllable interaction between growth factors and the material surface is of highest importance. Biocompatible diamond particles have recently become very interesting when studying these types of interactions [19]. Moreover, nanocrystalline diamond films, deposited onto titanium screws, have been proven to be osseoinductive [20,21]. However, there is at present a lack of scientific knowledge about diamond surfaces and their behavior in contact with biological molecules. One way to approach this problem is to use theoretical modeling as a highly valuable tool to study the interactions between diamond surfaces and adhered biomolecules.
With the purpose to tailor-make the medical implant surfaces by utilizing the unique properties and versatility of diamond, a theoretical investigation about the interaction between diamond and biomolecules have in the present study been performed. The main goal with the present study has been to find the most optimal combination of crystallite facet and terminating species for which the respective biomolecule will bind strong enough and at the same time stay biological active.
The main purpose with the present article is to theoretically outline the effect of diamond surface plane and termination on the binding of various important biomolecules. Diamond (111) and (100)-2x1 surface planes are then terminated with H, OH, Oontop, Obridge and NH2 species, respectively. The various biomolecules include BMP2, RGD, chitosan, heparin, AGP1, fibronectin and VEGF [21]. The theoretical calculations are based on an ab initio force field method.

2. Materials and Methods

It is, unfortunately, impractical to use first principle quantum mechanical method (like density functional theory (DFT) methods) for the present calculations. This is due to the large size of the models used in the present study (see Figure 1). However, these problems might be overcome by using force field (FF) methods. The advantage with force field methods is that they have the capacity to avoid the size restrictions of the DFT methods. However, the calculated bond energies (when using FF) has the tendency to become underestimated [22,23]. It is instead possible to use ab initio force fields that have been parameterized and validated using condensed-phase properties in addition to various ab initio and empirical data for molecules in isolation. This is a more accurate method to use for calculations of e.g., bond strengths in the systems of interests. The results in the present work have therefore been obtained by using the ab initio force field method within the program COMPASS (Condensed-phase Optimized Molecular Potentials for Atomistic Simulation Studies) from Accelrys, Inc. [24]. With this method it is possible to accurately predict structural properties for a broad range of biomolecules in isolation, as well as in condensed phases [25,26,27,28]. Since it is based on a force field method, it can be utilized for larger models up to 104 atoms.
The atomic charges used in the ab initio force field calculations where calculated by different means. The atomic charges for the diamond surface were calculated by using the DFT method (incorporated in CASTEP from Accelrys, Inc. [29,30,31]), whilst the atomic charges for the biomolecules were force field assigned in the FF calculations. The DFT method used in the present study is based on an ultrasoft pseudopotential plane-wave approach. The electronic exchange and correlation have been approximated using the Generalized Gradient Approximation as developed by Perdew, Burke and Ernzerhof (GGA-PBE) [32]. This specific approximation is supposed to be more accurate for the calculations of surface related properties [33]. Furthermore, the assigned atomic charges are Mulliken charges. Hirsfield charges would be an alternative, but that type of atomic charge often underestimates the charges distribution in molecules due to its dependence mainly on free-atom electron densities [34]. According to the Mulliken method for calculating atomic charges, a projection of the plane wave states onto the localized basis set was used in the present study [35].
For the ab initio FF optimization calculations, the threshold values were set to 8.4 × 10−5 kJ/mol (energy), 0.042 kJ/mol/Å (force) and 1.0 × 10−5 Å (displacement), respectively. An ordinary geometry optimization procedure initiated each simulation, which was followed by the real annealing process. The purpose this annealing process is to simulate the experimental heat treatment process in finally reaching the static state of the system under investigation. It is widely used in predicting protein adhesion affinities [26,36]. The starting temperatures in the annealing processes in the present study were set to 300 K and the mid-cycle temperature was set to 320 K. This is the temperature range that has been found appropriate to use for the physiological functionality of biomolecules. The duration of the simulations was ~25 ps and ended by an ordinary geometry optimization. The lengths of these simulations were rigorously tested and where then found long enough to reach energetic minima.
All atoms in the models, except the two bottom atomic layers, were allowed to move freely during the simulations. The two atomic bottom layers had to be kept fixed in order to simulate the continuation into a bulk structure. This type of constraint has earlier been shown to be valid for diamond systems [37].
The adhesion energies for the biomolecules, attached to the various diamond surfaces, were calculated by using Equation (1):
ΔEadhesion energy = (Ediamond-biomolecule − Esurface − Ebiomolecule)
where Ediamond-biomolecule is the energy for the whole system, Esurface is the energy for the diamond surface and Ebiomolecule is the energy for the biomolecule, respectively. The final structural geometries, obtained from a geometry optimization of the whole systems, where used for these single point energy calculations.
The construction and use of a realistic model are very important when performing theoretical investigations. A number of criteria must then be fulfilled. Earlier theoretical studies have shown that the models used for the diamond (100)-2x1 and (111) surfaces in the present study, is optimal to use for the present type of investigation [38]. The supercell dimensions for the diamond (100)-2x1 and (111) surfaces are: a = 80.46 Å, b = 90.52 Å and c = 85.11 Å and: a = 80.46 Å, b = 90.52 Å and c = 80.00 Å, respectively.
The lower part of the periodic surface slab is H-terminated. The reason for this termination is to simulate the continuation into bulk diamond. Moreover, the upper surface is either H–, Obridge–, Oontop–, OH–, or NH2–terminated (see Figure 1B,C). An earlier theoretical investigation showed that it is energetically possible (and even favorable) to terminate a diamond (100)-2x1 surface up to 100% with either H, O or OH species [39]. A 100% surface coverage by these species was therefore been used in the present study. It has also been found possible to experimentally and precisely, oxidize the diamond surfaces up to larger surface coverages [40].
The various biomolecules that have been used in the present study are: RGD, chitosan and heparin, as well as BMP2, AGP1, fibronectin and VEGF. The latter group of biomolecules are considerably smaller than the former ones (which are quite larger proteins). However, all of these biomolecules are growth factors which promote new blood vessel formation, cell growth and adhesion. 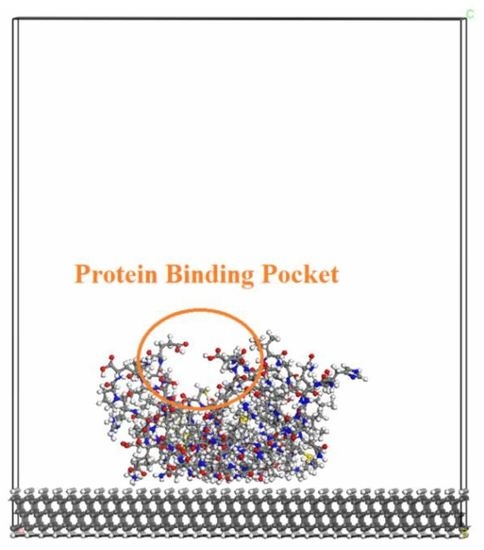The models of these biomolecules were taken from the Protein Data Bank [41]. These respective biomolecules were initially attached to the diamond surface with the protein-binding pocket positioned upwards with respect to the diamond surface (i.e., where ligands can easily bind to it). The purpose with this type of relative position was to keep the functionality of the biomolecule. A geometry-optimized structure of this type of system can be seen in Figure 1A. More specifically, it is a model of an H-terminated diamond (111) surface with an attached VEGF biomolecule.

3. Results

3.1. Introduction

As presented in Section 2, the models of the diamond//biomolecule systems were too big to use for the more accurate DFT methods. The methods that though can be used for these systems are the ab initio force field methods. In order to validate the usefulness of these methods, test calculations were performed in a recent work by the present authors [42]. Results from the more accurate ab initio FF method were then compared with the results obtained by using a hybrid DFT/FF method. The calculated adhesion energies for large physisorbed organic molecules onto differently terminated diamond surface planes thereby showed that the ab initio FF method is possible to use in the present study.

3.2. Adhesion Energies for Biomolecules Attached to Diamond (100)-2x1 and (111) Surfaces

The combined effect of surface termination and type of diamond surface plane has in the present study been theoretically investigated in order to investigate the adhesion strength for various biomolecules within the field of bone regeneration and vascularization. The diamond surface planes studied were the (111) surface and the 2x1-reconstructed (100) surface. Moreover, the terminating species include H, OH, Oontop, Obridge and NH2.

3.2.1. Effect of a Terminated Diamond (100)-2x1 Surface on Biomolecule Adsorption

For the (100)-2x1 surface (see Table 1), the adhesion energy of BMP2 was observed to be numerically higher than any of the other candidates. The adhesion energy was more than 2–3 times larger than the other biomolecules. This was the situation for the Oontop–, Obridge–, OH– and NH2–terminating species, with a special emphasize on the Oontop and Obridge species. On the contrary, the results for the H–terminating species was very similar to corresponding results for some of the other biomolecules; AGP, VEGF and fibronectin [2312 (BMP2), 1460 (AGP1), 1580 (VEGF) and 2090 (fibronectin) kJ/mol].
Van der Waals interactions between e.g., a biomolecule and a surface depend on the molecular weight of the biomolecule. Since the number of atoms within BMP2 (3860) is within the same order of magnitude as the other three proteins (AGP1 3383 atoms; Fibronectin 2944 atoms; VEGF 1531 atom), their respective molecular weight must also be similar (see Table 2). Hence, the difference in adsorption strengths for the various biomolecules, is not only due to differences in dispersive forces (i.e., Van der Waals interactions). There must also be a contribution of electrostatic interactions and/or hydrogen bonding to the extraordinary bond strength situation of BMP2. This assumption is strongly supported by the fact that BMP2 reacts especially strongly with the highly polar Oontop- and Obridge-terminated diamond surfaces. A strong binding of BMP2 onto a diamond surface has also been observed experimentally. This is an experimental result that strongly supports our theoretical observations. The bond strength between an attached BMP2 and the diamond surface were thereby measured by XPS-analysis (X-ray photoelectron spectroscopy) and the binding affinities were found to be much higher compared to the situation when using pure titanium as the solid surface. In addition, the bioactivity of BMP2 was retained as a result of the binding to the surface when using a diamond surface [43,44].
The second group of biomolecules, as shown in Table 1, is composed of VEGF, fibronectin and AGP1. The sizes of these biomolecules are around several thousands of atoms. Their adhesion energies are therefore quite large (750–2090 kJ/mol) and they thereby form a middle group (energetically) of biomolecules within the present study. For this middle group, H-termination was, with one exception, shown to result in the strongest adhesion energy to the diamond (100)-2x1 surface. The exception was the VEGF biomolecule, which showed the highest adhesion energy for NH2-termination. Since the molecular weight is most important for the Van der Waals-interaction between a diamond surface and the adhered biomolecule interaction and since VEGF is only half the size of angiopoietin 1, it would be expected that the adhesion energy of AGP1 is larger than for the VEGF biomoleule. However, the adhesion energies are, with the exception of Obridge-termination, very similar for these two biomolecules.
The third biomolecular group includes the much smaller polypeptides: RGD, chitosan and heparin. Their adhesion energies (10–800) were also found to be smaller in comparison to the other biomolecules, which is again a proof of the circumstance that the sizes of the biomolecules are of utter importance for size of the Van der Waals interactions. Furthermore, the H-termination was shown to give the largest adhesion energy for all of these polypeptides.

3.2.2. Effect of a Terminated Diamond (111) Surface on Biomolecule Adsorption

The adhesion energies for the different biomolecules adsorbed onto the diamond (111) surface, are shown in Table 3. It has earlier been shown that the diamond (111) surface is more reactive than the (100)-2x1 surface [45]. It is the reactivity of the individual surface carbon atoms that is referred to. Moreover, the densities of surface C atoms on the (111) and (100)-2x1 surfaces, are 0.19 and 0.16 atoms/Å2, respectively. The combination of a larger chemical reactivity of individual surface C atoms and a larger surface atom density for the (111) surface, is thereby expected to result in larger adhesion energies for the biomolecules. This was especially the situation with the largest biomolecules that covered a larger part of the diamond surfaces (BMP2, VEGF, fibronectin, AGP1); 1150–8200 kJ/mol for the (111) surface and 750–5480 kJ/mol for the (100)-2x1 surface.
As was the situation for the diamond (100)-2x1 surface, three adhesion energy groupings of biomolecules were found for the diamond (111) surface (also here displaying the importance of molecular weight for the surface-biomolecule Van der Waals interactions). As can be seen in Table 3, it is obvious that Obridge–termination is the preferred type of termination. This is in fact the situation for BMP2 (which from here on is called group 1) and for all molecules in group 2. Moreover, H–termination was, for group 1, found to give the weakest adhesion energy. Also, fibronectin VEGF and (in group 2) were shown to have the weakest adhesion energies for an H-terminated diamond (111). On the contrary, AGP1 showed the weakest adhesion for Oontop–termination. In the third and most weakly bound group of biomolecule adsorbates, heparin and chitosan were shown to both prefer Obridge–termination and disfavor H-termination. In addition, H–termination was energetically favored for RGD. The lowest adhesion energy in the present study was observed for the RGD peptide onto an Oontop–terminated (111) surface, with a numerical value as low as 12 kJ/mol.

3.3. Adhesion Energies for Various Types of Surface Termination

For H–terminated diamond surfaces, the calculated adhesion energies for adsorbed BMP2, AGP1 and VEGF biomolecules were found to be larger for the diamond (111) surface than for diamond (100)-2x1 (see Figure 2). The situation is, however, the opposite for RGD and Fibronectin. As stated above, the adhesion energies are usually more pronounced for diamond (111) surfaces due to the combination of both its higher surface carbon density and the large chemical reactivity of each individual surface C atom (i.e., the (111) surface has a larger surface energy as compared to (100)-2x1). However, an exception from this rule is here evident for RGD and Fibronectin and the explanation may be an existence of electrostatic interactions between the H–terminated surface and these biomolecules. It should also be stressed that the difference in calculated adhesion energy, with respect to the other biomolecules, is relatively small for both of these biomolecules. For OH–termination, the calculated adhesion energies for all biomolecules attached to diamond (111) were found to be larger than for those attached to diamond (100)-2x1. Moreover, the results for the Oontop–termination showed the same major trend as for the OH–termination.
As was the situation with the OH–, Oontop– and Obridge–terminations, the adhesion energies for all biomolecules attached to an NH2–terminated diamond (111) surface were observed to be numerically similar to, or larger than, the corresponding adhesion energies for diamond (100)-2x1. It should also be noted that the adhesion energies for both the diamond (100)-2x1 and (111) surfaces, were observed to be not that large (i.e., almost same) for the smallest biomolecular groups.

3.4. Adhesion Energies for Individual Biomolecules

As presented in Section 3.2. Adhesion energies for biomolecules attached to diamond (100)-2x1 and (111) surfaces, the adhesion energies for the biomolecules BMP2, VEGF, AGP1, fibronectin, heparin, chitosan and RGD have generally been found to be larger for the diamond (111) surface than for diamond (100)-2x1 (see Figure 3). This is especially the situation for the larger biomolecules (i.e., for fibronectin, VEGF, AGP1 and BMP2. As discussed above, this may be explained by differences in surface energy for the two surface planes. Two exceptions to this general observation are the adhesion of RGD and fibronectin to H-terminated diamond surfaces. As can be seen in Figure 2a, it is the adsorption of the various biomolecules to an H-terminated (100)-2x1 surface that results in a somewhat more irregular shape of the adsorption energy curve. The reason to this observation might be changes in degree of surface reconstruction. A de-reconstructed diamond (100) surface is more reactive than a 2x1-reconstructed (100) surface. In addition, BMP2 shows much larger adhesion energies as compared to the rest of the growth factors, which correspond to earlier experimental findings [44]. Specifically, for the BMP2 adhesion onto the diamond (111) surface, the order of adhesion energy for the various surface-terminating species was calculated as Obridge > OH > NH2 > Oontop > H. However, the corresponding order for the diamond (100)-2x1 surface was observed to be different; Oontop > Obridge > NH2 > OH > H. More specifically, it is the OH– and Oontop–termination that will break an otherwise perfect similarity in trend between these two diamond surfaces. For the situation with VEGF, the order of preference for the various surface termination species onto the diamond (111) surface was found to be Obridge > NH2 > Oontop> OH > H. The corresponding order for the diamond (100)-2x1 surface is NH2 > Oontop > H > Obridge > OH. For this biomolecule, in addition to OH-termination and oxygen in bridge positions (i.e., Obridge–termination) that will break an otherwise perfect similarity in trend between these two diamond surfaces.
The trends in adhesion energy as a function of surface termination type, were also observed to be very similar for the AGP1 protein: Obridge > H > NH2 > OH > Oontop (diamond (111)) and Obridge > H > NH2 > Oontop > OH (diamond (100)-2x1). It is here only the Oontop–termination that will break an otherwise perfect similarity in trend between these two diamond surfaces.
The corresponding trends in adhesion energies were observed to be completely different for fibronectin. The order of adhesion energies for the diamond (111) surface was calculated as Obridge > NH2 > OH > Oontop > H. Moreover, for the diamond (100)-2x1 surface it was H > NH2 > Obridge > Oontop > OH. Experimental studies using AFM (atomic force microscopy) and FTIR (Fourier-transform infrared) spectroscopy have indicated that fibronectin can absorb onto Si surfaces. The surface chemical properties (especially the wettability) were observed to play an important role in keeping the structure and functionality of the protein. For a hydrophilic Si surface, the alpha-helix content in adsorbed fibronectin was observed to be similar to the original (molecular) structure with a good consistency [46].
For heparin, the order of preferences for adhesion onto the (111) surface was observed to be Obridge > NH2 > OH > Oontop > H and for diamond (100)-2x1 surface it was Oontop > H > NH2 > Obridge > OH. As was the situation for fibronectin, these two different trends are completely dissimilar. However, the orders of adhesion energies, when comparing the adhesion of fibronectin and heparin onto diamond (111), were found to be identical. For the situation with diamond (100)-2x1, the orders were identical, with the exception for Oontop–termination.
For chitosan, the calculated adhesion energies for the diamond (111) and (100)-2x1 surfaces were; Obridge > NH2 > OH > Oontop > H and H > Oontop > NH2 > Obridge > OH, respectively. As was the situation for heparin and fibronectin, these two different trends are completely dissimilar. Moreover, the orders of adhesion energies, when comparing the adhesion of fibronectin, heparin and chitosan onto diamond (111), were found to be identical. For the situation with diamond (100)-2x1, the orders were also here identical with the exception for Oontop–termination.
For the RGD peptide, the order of preferences for adhesion to variously terminated diamond (111) surfaces were calculated to be H > Obridge > OH > NH2 > Oontop and for terminated diamond (100)-2x1 surfaces it became H > Oontop > Obridge > OH > NH2. For this biomolecule, it is the H-termination (diamond (111)) and H– and OH–termination (diamond (100)-2x1), that will break an otherwise perfect similarity in trend between these two diamond surfaces.

4. Discussion

With the purpose to tailor-make the bone implant surfaces by using the unique surface properties of diamond, a theoretical investigation has in the present study been performed in order to more deeply study the interaction between diamond and various biomolecules. More specifically, the main goal has been to find the most optimal combination of diamond surface plane and terminating species for which various biomolecules will bind strong enough and at the same time stay biological active.
The H, OH, Oontop, Obridge and NH2 species were in the present study used to completely terminate the diamond (111) and (100)-2x1 surface, respectively. The biomolecules that were attached to these terminated surfaces were BMP2, RGD, chitosan, heparin, AGP1, fibronectin or VEGF. The calculated results were obtained by using the ab initio force field methods within the COMPASS software from Accelrys, Inc.
The results show that the sizes of the individual biomolecules are very important for the adhesion energies. Three groups of biomolecules were observed for both the diamond (100)-2x1 and (111) planes. The largest biomolecular, BMP2, resulted in the strongest binding. On the contrary, the weakest binding was obtained for the smaller polypeptides: RGD, chitosan and heparin. A third group, with adhesion energies somewhere in between the other two groups, contained VEGF, fibronectin and AGP1.
The combination of diamond surface plane and termination type resulted in predominant variations in adhesion energies for the various biomolecules. In relation to diamond (100)-2x1, OH–, Oontop–, Obridge– and NH2–terminated diamond (111) surfaces resulted in stronger bonding with the biomolecules. The situation was different for H-terminated surfaces. The biomolecules RGD and fibronectin were observed to bind stronger onto the H–terminated diamond (100)-2x1 surface. An overview of the combined diamond plane—surface termination impact on the adhesion energy, for various biomolecules, is shown below.
For the BMP2 biomolecule, the order of adhesion energy for the diamond (111) surface was: Obridge > OH > NH2 > Oontop > H and for the diamond (100)-2x1 surface it was: Oontop > Obridge > NH2 > OH > H. For the VEGF biomolecule, the order of adhesion energies onto the diamond (111) surface was: Obridge > NH2 > Oontop> OH> H and for the diamond (100)-2x1 surface it was: NH2 > Oontop > H >Obridge > OH. For the AGP1 biomolecule, the trends in adhesion energy for both the diamond (100)-2x1 and (111) surfaces were found to be identical; Obridge > H > NH2 > OH > Oontop. For the fibronectin biomolecule, the order of adhesion energies onto the diamond (111) surface was: Obridge > NH2 > OH > Oontop > H. The corresponding order for the diamond (100)-2x1 surface was: H > NH2 > Obridge > Oontop > OH. For the heparin biomolecule, the order of adhesion energies onto the diamond (111) surface was: Obridge > NH2 > OH > Oontop > H and for the diamond (100)-2x1 surface it was: Oontop > H > NH2 > Obridge > OH. For the chitosan biomolecule, the order of adsorption energies for diamond (111) was: Obridge > NH2 > OH > Oontop > H and for diamond (100)-2x1 it was: H > Oontop > NH2 > Obridge > OH. The weakest adhesion energies in the present study was obtained for the RGD peptide, with the following result for the diamond (111) surface: H > Obridge > OH > NH2 > Oontop. This is to be compared with the results for diamond (100)-2x1: H > Oontop > Obridge > OH > NH2.
There are many factors that might influence the adhesion energy for biomolecules attached to a diamond surface. The most important ones are (i) size of biomolecule, (ii) surface plane, (iii) surface termination and (iv) surface reconstruction. The influences of these parameters have been discussed above in close connection to the obtained results in the present study. General trends were thereby found for each of the different biomolecules. However, other factors might influence the obtained results, thereby introducing exceptions to the general trends. For instance, the interactions between the diamond surface and the biomolecules may cause changes in the surface reconstructions (i.e., the 2x1-reconstructed (100) surface may de-reconstruct to a (100) surface). Moreover, the initial terminating species may undergo changes and thereby form another type of termination (i.e., the very reactive Obridge–terminated diamond (111) surface may become Oontop–terminated). It is very difficult to explain all individual results in the present study, but plausible explanations can be given. For instance, the larger adhesion energies for the larger biomolecules being attached to an initial Obridge–terminated diamond (111) surface might be due to the transformation to the more stable Oontop–terminated diamond (111) surface. Moreover, the reason to the somewhat larger adhesion energies for the OH– and NH2–terminated diamond (111) surface might be the formation of a larger extent of H bonds between the biomolecule and the surface. Another explanation could be interfacial reactions with the occurrence of an H transfer from the surface to the respective biomolecule. Due to the size of the model systems used in the present investigation, it is practically not possible to analyze these influencing factors more in detail.
The main result from the following study is that H-termination is generally good to use for the diamond (100)-2x1 surface, whilst Obridge–termination is a better choice for the diamond (111) surface. In addition, BMP2 shows the absolutely highest adhesion energies of all candidates in the present study.

Author Contributions

K.L. was supervising the work. Y.T. performed the calculations. K.L. and Y.T. wrote the paper.

Funding

This research was funded by the European Union Seventh Frame programme (FP7) with grant number 242175. The APC was funded by Uppsala University.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Hartl, A.; Schmich, E.; Garrido, J.A.; Hernando, J.; Catharino, S.C.; Walter, S.; Feulner, P.; Kromka, A.; Steinmuller, D.; Stutzmann, M. Protein-modified nanocrystalline diamond thin films for biosensor applications. Nat. Mater. 2004, 3, 736–742. [Google Scholar] [CrossRef] [PubMed]
  2. Kwok, S.C.; Wang, J.; Chu, P.K. Surface energy, wettability, and blood compatibility phosphorus doped diamond-like carbon films. Diam. Relat. Mater. 2005, 14, 78–85. [Google Scholar] [CrossRef]
  3. Zhu, D.; Zhang, L.; Ruther, R.E.; Hamers, R.J. Photo-illuminated diamond as a solid-state source of solvated electrons in water for nitrogen reduction. Nat. Mater. 2013, 12, 836–841. [Google Scholar] [CrossRef] [PubMed]
  4. McEvoy, J.P.; Gascon, J.A.; Batista, V.S.; Brudvig, G.W. The mechanism of photosynthetic water splitting. Photochem. Photobiol. Sci. 2005, 4, 940–949. [Google Scholar] [CrossRef] [PubMed]
  5. Yang, W.; Auciello, O.; Butler, J.E.; Cai, W.; Carlisle, J.A.; Gerbi, J.E.; Gruen, D.M.; Knickerbocker, T.; Lasseter, T.L.; Russell, J.N.; et al. DNA-modified nanocrystalline diamond thin-films as stable, biologically active substrates. Nat. Mater. 2002, 1, 253–257. [Google Scholar] [CrossRef] [PubMed]
  6. Szunerits, S.; Nebel, C.E.; Hamers, R.J. Surface functionalization and biological applications of CVD diamond. MRS Bull. 2014, 39, 517–524. [Google Scholar] [CrossRef]
  7. Willey, T.M.; Bostedt, C.; van Buuren, T.; Dahl, J.E.; Liu, S.G.; Carlson, R.M.K.; Terminello, L.J.; Möller, T. Molecular Limits to the Quantum Confinement Model in Diamond Clusters. Phys. Rev. Lett. 2005, 95, 113401. [Google Scholar] [CrossRef] [PubMed]
  8. Yuan, T.; Larsson, K. Theoretical Study of Size Effects on Surface Chemical Properties for Nanoscale Diamond Particles. J. Phys. Chem. C 2014, 118, 26061–26069. [Google Scholar] [CrossRef]
  9. May, P.W.; Stone, J.C.; Ashfold, M.N.R.; Hallam, K.R.; Wang, W.N.; Fox, N.A. The effect of diamond surface termination species upon field emission properties. Diam. Relat. Mater. 1998, 7, 671–676. [Google Scholar] [CrossRef]
  10. Mackey, B.L.; Russell, J.N.; Crowell, J.E., Jr.; Butler, J.E. Effect of surface termination on the electrical conductivity and broad-band internal infrared reflectance of a diamond (110) surface. Phys. Rev. B 1995, 52, R17009–R17012. [Google Scholar] [CrossRef]
  11. Martin, H.B.; Argoitia, A.; Landau, U.; Anderson, A.B.; Angus, J.C. Hydrogen and Oxygen Evolution on Boron-Doped Diamond Electrodes. J. Electrochem. Soc. 1996, 143, L133–L136. [Google Scholar] [CrossRef]
  12. Nebel, C.E.; Ertl, F.; Sauerer, C.; Stutzmann, M.; Graeff, C.F.O.; Bergonzo, P.; Williams, O.A.; Jackman, R.B. Low temperature properties of the p-type surface conductivity of diamond. Diam. Relat. Mater. 2002, 11, 351–354. [Google Scholar] [CrossRef]
  13. Maier, F.; Ristein, J.; Ley, L. Electron affinity of plasma-hydrogenated and chemically oxidized diamond (100) surfaces. Phys. Rev. B 2001, 64, 165411. [Google Scholar] [CrossRef]
  14. Azevedo, A.F.; Baldan, M.R.; Ferreira, N.G. Nanodiamond Films for Applications in Electrochemical Systems. Int. J. Electrochem. 2012, 16. [Google Scholar] [CrossRef]
  15. Hierholzer, C.; Sama, D.; Toro, J.B.; Peterson, M.; Helfet, D.L. Plate Fixation of Ununited Humeral Shaft Fractures: Effect of Type of Bone Graft on Healing. JBJS 2006, 88, 1446–1447. [Google Scholar]
  16. Klaus, T.; Joerger, R.; Olsson, E.; Granqvist, C.-G. Silver-based crystalline nanoparticles, microbially fabricated. Proc. Nat. Acad. Sci. USA 1999, 96, 13611–13614. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  17. Schrand, A.M.; Dai, L.; Schlager, J.J.; Hussain, S.M.; Osawa, E. Differential biocompatibility of carbon nanotubes and nanodiamonds. Diam. Relat. Mater. 2007, 16, 2118–2123. [Google Scholar] [CrossRef]
  18. Mistry, A.S.; Pham, Q.P.; Schouten, C.; Yeh, T.; Christenson, E.M.; Mikos, A.G.; Jansen, J.A. In vivo bone biocompatibility and degradation of porous fumarate-based polymer/alumoxane nanocomposites for bone tissue engineering. J. Biomed. Mater. Res. Part. A 2010, 92, 451–462. [Google Scholar] [CrossRef]
  19. Kloss, F.R.; Singh, S.; Hächl, O.; Rentenberger, J.; Auberger, T.; Kraft, A.; Klima, G.; Mitterlechner, T.; Steinmüller-Nethl, D.; Lethaus, B.; et al. BMP-2 immobilized on nanocrystalline diamond–coated titanium screws; demonstration of osteoinductive properties in irradiated bone. Head Neck 2013, 35, 235–241. [Google Scholar] [CrossRef]
  20. Ivanova, L.; Popov, C.; Kolev, I.; Shivachev, B.; Karadjov, J.; Tarassov, M.; Kulisch, W.; Reithmaier, J.P.; Apostolova, M.D. Nanocrystalline diamond containing hydrogels and coatings for acceleration of osteogenesis. Diam. Relat. Mater. 2011, 20, 165–169. [Google Scholar] [CrossRef]
  21. Fromell, K.; Forsberg, P.; Karlsson, M.; Larsson, K.; Nikolajeff, F.; Baltzer, L. Designed protein binders in combination with nanocrystalline diamond for use in high-sensitivity biosensors. Anal. Bioanal. Chem. 2012, 404, 1643–1651. [Google Scholar] [CrossRef] [PubMed]
  22. Lewars, E.G. Computational Chemistry: Introduction to the Theory and Applications of Molecular and Quantum Mechanics; Springer International Publishing AG: Basel, Switzerland, 2016. [Google Scholar]
  23. Fang, H.; Kamakoti, P.; Zang, J.; Cundy, S.; Paur, C.; Ravikovitch, P.I.; Sholl, D.S. Prediction of CO2 Adsorption Properties in Zeolites Using Force Fields Derived from Periodic Dispersion-Corrected DFT Calculations. J. Phys. Chem. C 2012, 116, 10692–10701. [Google Scholar] [CrossRef]
  24. Sun, H. COMPASS: An ab Initio Force-Field Optimized for Condensed-Phase ApplicationsOverview with Details on Alkane and Benzene Compounds. J. Phys. Chem. B 1998, 102, 7338–7364. [Google Scholar] [CrossRef]
  25. McQuaid, M.J.; Sun, H.; Rigby, D. Development and validation of COMPASS force field parameters for molecules with aliphatic azide chains. J. Comput. Chem. 2004, 25, 61–71. [Google Scholar] [CrossRef] [PubMed]
  26. Wang, S.; Humphreys, E.S.; Chung, S.-Y.; Delduco, D.F.; Lustig, S.R.; Wang, H.; Parker, K.N.; Rizzo, N.W.; Subramoney, S.; Chiang, Y.-M.; et al. Peptides with selective affinity for carbon nanotubes. Nat. Mater. 2003, 2, 196–200. [Google Scholar] [CrossRef] [PubMed]
  27. Jiang, J.-X.; Su, F.; Trewin, A.; Wood, C.-D.; Campbell, N.-L.; Niu, H.; Dickinson, C.; Ganin, A.Y.; Rosseinsky, M.J.; Khimyak, Y.Z.; et al. Conjugated Microporous Poly(aryleneethynylene) Networks. Angew. Chem. Int. Ed. 2007, 46, 8574–8578. [Google Scholar] [CrossRef]
  28. Jiang, J.-X.; Su, F.; Trewin, A.; Wood, C.D.; Niu, H.; Jones, J.T.A.; Khimyak, Y.Z.; Cooper, A.I. Synthetic Control of the Pore Dimension and Surface Area in Conjugated Microporous Polymer and Copolymer Networks. J. Am. Chem. Soc. 2008, 130, 7710–7720. [Google Scholar] [CrossRef] [PubMed]
  29. Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electron-gas correlation energy. Phys. Rev. B 1992, 45, 13244–13249. [Google Scholar] [CrossRef]
  30. Kohn, W.; Sham, L.J. Self-Consistent Equations Including Exchange and Correlation Effects. Phys. Rev. A 1965, 140, 1133–1138. [Google Scholar] [CrossRef]
  31. Clark, S.J.; Segall, M.D.; Pickard, C.J.; Hasnip, P.J.; Probert, M.I.; Refson, K.; Payne, M.C. First principles methods using CASTEP. Zeitschrift für Kristallographie 2005, 220, 567–570. [Google Scholar] [CrossRef]
  32. Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed]
  33. Hammer, B.; Hansen, L.B.; Nørskov, J.K. Improved adsorption energetics within density-functional theory using revised Perdew-Burke-Ernzerhof functionals. Phys. Rev. B 1999, 59, 7413–7421. [Google Scholar] [CrossRef] [Green Version]
  34. Davidson, D.; Chakravorty, S. A test of the Hirshfeld definition of atomic charges and moments. Theor. Chim. Acta 1992, 83, 319–330. [Google Scholar] [CrossRef]
  35. Mulliken, R.S. Electronic Population Analysis on LCAO–MO Molecular Wave Functions. I. J. Chem. Phys. 1955, 23, 1833–1840. [Google Scholar] [CrossRef]
  36. Euston, S.R. Molecular Dynamics Simulation of Protein Adsorption at Fluid Interfaces: A Comparison of All-Atom and Coarse-Grained Models. Biomacromolecules 2010, 11, 2781–2787. [Google Scholar] [CrossRef] [PubMed]
  37. Petrini, D.; Larsson, K. Electron Transfer from a Diamond (100) Surface to an Atmospheric Water Adlayer:  A Quantum Mechanical Study. J. Phys. Chem. C 2007, 111, 13804–13812. [Google Scholar] [CrossRef]
  38. Petrini, D.; Larsson, K. Theoretical Study of the Thermodynamic and Kinetic Aspects of Terminated (111) Diamond Surfaces. J. Phys. Chem. C 2008, 112, 3018–3026. [Google Scholar] [CrossRef]
  39. Petrini, D.; Larsson, K. A Theoretical Study of the Energetic Stability and Geometry of Hydrogen- and Oxygen-Terminated Diamond (100) Surfaces. J. Phys. Chem. C 2006, 111, 795–801. [Google Scholar] [CrossRef]
  40. Krueger, A.; Lang, D. Functionality is Key: Recent Progress in the Surface Modification of Nanodiamond. Adv. Func. Mater. 2012, 22, 890–906. [Google Scholar] [CrossRef]
  41. Available online: www.pdb.org (accessed on 12 June 2014).
  42. Larsson, K.; Tian, Y. Effect of surface termination on the reactivity of nano-sized diamond particle surfaces for bioapplications. Carbon 2018, 134, 244–254. [Google Scholar] [CrossRef]
  43. Kloss, F.R.; Gassner, R.; Preiner, J.; Ebner, A.; Larsson, K.; Hächl, O.; Tuli, T.; Rasse, M.; Moser, D.; Laimer, K.; et al. The role of oxygen termination of nanocrystalline diamond on immobilisation of BMP-2 and subsequent bone formation. Biomaterials 2008, 29, 2433–2442. [Google Scholar] [CrossRef] [PubMed] [Green Version]
  44. Steinmuller-Nethl, D.; Kloss, F.R.; Najam-Ul-Haq, M.; Rainer, M.; Larsson, K.; Linsmeier, C.; Kohler, G.; Fehrer, C.; Lepperdinger, G.; Liu, X.; et al. Strong binding of bioactive BMP-2 to nanocrystalline diamond by physisorption. Biomaterials 2006, 27, 4547–4556. [Google Scholar] [CrossRef] [PubMed]
  45. Petrini, D.; Larsson, K. Origin of the Reactivity on the Nonterminated (100), (110), and (111) Diamond Surfaces: An Electronic Structure DFT Study. J. Phys. Chem. C 2008, 112, 14367–14376. [Google Scholar] [CrossRef]
  46. Tunc, S.; Maitz, M.F.; Steiner, G.; Vazquez, L.; Pham, M.T.; Salzer, R. In situ conformational analysis of fibrinogen adsorbed on Si surfaces. Colloids and surfaces. Colloids Surf B Biointerfaces 2005, 42, 219–225. [Google Scholar] [CrossRef] [PubMed]
Materials 12 00865 g001 550
Figure 1. (A) Model demonstrating a 2x1-reconstructed diamond (111) surface that is to 100% terminated with H atoms and thereafter attached to a Vascular Endothelial Growth Factor (VEGF) molecule. The orientation of the biomolecule is such that the protein binding pocket is on top and far away from the surface. (B) Five different termination species adsorbed onto a 2x1-reconstructed diamond (100) surface: (a) H, (b) OH, (c) NH2, (d) Obridge and (e) Oontop. (C) Five different termination species that are adsorbed to a diamond (111) surface: (a) H, (b) OH, (c) Oontop, (d) NH2 and (e) Obridge.
Figure 1. (A) Model demonstrating a 2x1-reconstructed diamond (111) surface that is to 100% terminated with H atoms and thereafter attached to a Vascular Endothelial Growth Factor (VEGF) molecule. The orientation of the biomolecule is such that the protein binding pocket is on top and far away from the surface. (B) Five different termination species adsorbed onto a 2x1-reconstructed diamond (100) surface: (a) H, (b) OH, (c) NH2, (d) Obridge and (e) Oontop. (C) Five different termination species that are adsorbed to a diamond (111) surface: (a) H, (b) OH, (c) Oontop, (d) NH2 and (e) Obridge.
Materials 12 00865 g001
Materials 12 00865 g002 550
Figure 2. Adhesion energies (in kJ/mol) for various growth factors attached to diamond (100) and (111) surfaces, being terminated with (a) H, (b) OH, (c) Oontop, (d) Obridge, or (e) NH2 species.
Figure 2. Adhesion energies (in kJ/mol) for various growth factors attached to diamond (100) and (111) surfaces, being terminated with (a) H, (b) OH, (c) Oontop, (d) Obridge, or (e) NH2 species.
Materials 12 00865 g002
Materials 12 00865 g003 550
Figure 3. Adhesion energies as a function of surface termination species for seven different biomolecules attached to diamond (111) and (100)-2x1, respectively; (a) BMP2, (b) VEGF, (c) AGP1, (d) fibronectin, (e) heparin, (f) chitosan and (g) RGD peptide. The surface terminating species are H, OH, Oontop, Obridge and NH2.
Figure 3. Adhesion energies as a function of surface termination species for seven different biomolecules attached to diamond (111) and (100)-2x1, respectively; (a) BMP2, (b) VEGF, (c) AGP1, (d) fibronectin, (e) heparin, (f) chitosan and (g) RGD peptide. The surface terminating species are H, OH, Oontop, Obridge and NH2.
Materials 12 00865 g003
Table
Table 1. Adhesion energy for various biomolecules attached onto an X-terminated diamond (100)-2x1 surface (X = H, OH, Oontop, Obridge and NH2). The biomolecules include VEGF, BMP2, AGP1, fibronectin, heparin, chitosan and RGD. The unit is kJ/mol.
Table 1. Adhesion energy for various biomolecules attached onto an X-terminated diamond (100)-2x1 surface (X = H, OH, Oontop, Obridge and NH2). The biomolecules include VEGF, BMP2, AGP1, fibronectin, heparin, chitosan and RGD. The unit is kJ/mol.
Diamond (100)-2x1HOHOontopObridgeNH2
BMP223122480548052023803
VEGF1580970164011401840
Fibronectin2090805120414501195
AGP1146075083814481115
Heparin601495520512535
Chitosan520480525485535
RGD8003047046010
Table
Table 2. Number of atoms for the biomolecules BMP2, VEGF, fibronectin, AGP1, heparin, chitosan and RGD.
Table 2. Number of atoms for the biomolecules BMP2, VEGF, fibronectin, AGP1, heparin, chitosan and RGD.
BiomoleculesNumber of Atoms in the Molecular Unit
BMP23860
VEGF1531
Fibronectin2944
AGP13383
Heparin 112
Chitosan16
RGD46
Table
Table 3. Adhesion energy for various biomolecules attached onto an X-terminated diamond (111) surface (X = H, OH, Oontop, Obridge and NH2). The biomolecules include VEGF, BMP2, AGP1, fibronectin, heparin, chitosan and RGD. The unit is kJ/mol.
Table 3. Adhesion energy for various biomolecules attached onto an X-terminated diamond (111) surface (X = H, OH, Oontop, Obridge and NH2). The biomolecules include VEGF, BMP2, AGP1, fibronectin, heparin, chitosan and RGD. The unit is kJ/mol.
Diamond (111)HOHOontopObridgeNH2
BMP258008007642011,9406428
VEGF19232040204323022172
Fibronectin11032038200328032401
AGP29401980196635432008
Heparin641639635704680
Chitosan502605603651602
RGD6412481245858

Share and Cite

MDPI and ACS Style

Tian, Y.; Larsson, K. Effect by Diamond Surface Modification on Biomolecular Adhesion. Materials 2019, 12, 865. https://doi.org/10.3390/ma12060865

AMA Style

Tian Y, Larsson K. Effect by Diamond Surface Modification on Biomolecular Adhesion. Materials. 2019; 12(6):865. https://doi.org/10.3390/ma12060865

Chicago/Turabian Style

Tian, Yuan, and Karin Larsson. 2019. "Effect by Diamond Surface Modification on Biomolecular Adhesion" Materials 12, no. 6: 865. https://doi.org/10.3390/ma12060865

APA Style

Tian, Y., & Larsson, K. (2019). Effect by Diamond Surface Modification on Biomolecular Adhesion. Materials, 12(6), 865. https://doi.org/10.3390/ma12060865

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop