Parametric Formulae for Elastic Stress Concentration Factor at the Weld Toe of Distorted Butt-Welded Joints
Abstract
:1. Introduction
2. Finite Element Analysis
2.1. Geometric Model
2.2. Finite Element Model
2.2.1. Finite Element Model for Undistorted Butt-Welded Joints
2.2.2. Finite Element Model for Distorted Butt-Welded Joints
2.3. Application Ranges of Parameters
- Weld toe radius ρ/ts: 0.01–0.40;
- Weld reinforcement height δ/ts: 0.05–0.40;
- Width of weld seam W/ts: 1.0–2.0;
- Flank angle θ: 10°–60°;
- Distortion angle α: 0–3°; and
- Total length of specimen Lfree/ts: 10.0–40.0.
3. Elastic SCF Formulae for Undistorted Butt-Welded Joints
3.1. Overview on Existing Kt Formulae
3.2. The Influence of Weld Width
3.3. Kt Parametric Formula
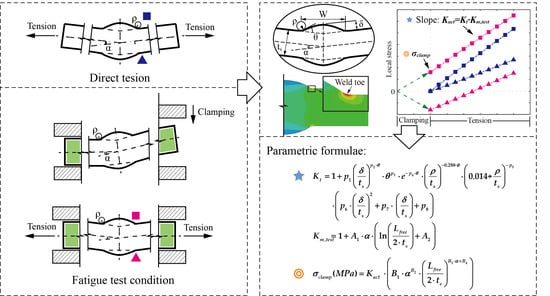
4. Elastic SCF and Clamping Stress Formulae for Distorted Butt-Welded Joints
4.1. Definition of Km,test and Kact
4.2. Km,test, Kact, and σclamp Parametric Formulae
5. Conclusions
- Weld toe radius ρ/ts: 0.01–0.40;
- Weld reinforcement height δ/ts: 0.05–0.40;
- Width of weld seam W/ts: 1.0–2.0;
- Flank angle θ: 10°–60°;
- Distortion angle α: 0–3°; and
- Total length of specimen Lfree/ts: 10.0–40.0.
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Caccese, V.; Blomquist, P.A.; Berube, K.A.; Webber, S.R.; Orozco, N.J. Effect of weld geometric profile on fatigue life of cruciform welds made by laser/GMAW processes. Mar. Struct. 2006, 19, 1–22. [Google Scholar] [CrossRef]
- da Silva, A.L.L.; Correia, J.A.F.O.; de Jesus, A.M.P.; Lesiuk, G.; Fernandes, A.A.; Calçada, R.; Berto, F. Influence of fillet end geometry on fatigue behaviour of welded joints. Int. J. Fatigue 2019, 123, 196–212. [Google Scholar] [CrossRef]
- Pouget, G.; Reynolds, A.P. Residual stress and microstructure effects on fatigue crack growth in AA2050 friction stir welds. Int. J. Fatigue 2008, 30, 463–472. [Google Scholar] [CrossRef]
- Fukaura, K.; Yokoyama, Y.; Yokoi, D.; Tsujii, N.; Ono, K. Fatigue of cold-work tool steels: Effect of heat treatment and carbide morphology on fatigue crack formation, life, and fracture surface observations. Metall. Mater. Trans. A 2004, 35, 1289–1300. [Google Scholar] [CrossRef]
- Yadollahi, A.; Shamsaei, N.; Thompson, S.M.; Elwany, A.; Bian, L. Effects of building orientation and heat treatment on fatigue behavior of selective laser melted 17-4 PH stainless steel. Int. J. Fatigue 2017, 94, 218–235. [Google Scholar] [CrossRef]
- Li, W.; Sakai, T.; Li, Q.; Lu, L.T.; Wang, P. Effect of loading type on fatigue properties of high strength bearing steel in very high cycle regime. Mater. Sci. Eng. A 2011, 528, 5044–5052. [Google Scholar] [CrossRef]
- Radaj, D. Design and Analysis of Fatigue Resistant Welded Structures; Abington Publishing: Abington Cambridge, UK, 1990. [Google Scholar]
- Neuber, H. Über die Berücksichtigung der spannungskonzentration bei festigkeitsberechnungen [Consideration of the stress concentration in strength calculations]. Konstruktion 1968, 20, 245–251. [Google Scholar]
- Fricke, W. Guideline for the Fatigue Assessment by Notch Stress Analysis for Welded Structures; Woodhead Publishing Limited: Sawston Cambridge, UK, 2012. [Google Scholar]
- Iida, K.; Uemura, T. Stress concentration factor formulae widely used in Japan. Fatigue Fract. Engng. Mater. Struct. 1996, 19, 779–786. [Google Scholar] [CrossRef]
- Ushirokawa, O.; Nakayama, E. Stress concentration factor at welded Joints. Ishikawajima-Harima Gihou (Technical Report) 1983, 23, 351–355. (In Japanese) [Google Scholar]
- Nishida, M. Stress Concentration; Morikita Publishing Co.: Chiyoda-ku, Tokyo, Japan, 1967. (In Japanese) [Google Scholar]
- Tsuji, I. Estimation of stress concentration factor at weld toe of non-load carrying fillet welded joints. J. West-Jpn. Soc. Nav. Archit. 1990, 80, 241–251. (In Japanese) [Google Scholar]
- Lawrence, F.V.; Ho, N.J.; Mazumdar, P.K. Predicting the fatigue resistance of welds. Ann. Rev. Mater. Sci. 1981, 11, 401–425. [Google Scholar] [CrossRef]
- Yung, J.Y.; Lawrence, F.V. Analytical and graphical aids for the fatigue design of weldments. Fatigue Fract. Engng. Mater. Struct. 1985, 8, 223–241. [Google Scholar] [CrossRef]
- Monahan, C.C. Early fatigue crack growth at welds. Compt. Mech. 1995, 26, 112–116. [Google Scholar]
- Brennan, F.P.; Peleties, P.; Hellier, A.K. Predicting weld toe stress concentration factors for T and skewed T-joint plate connections. Int. J. Fatigue 2000, 22, 573–584. [Google Scholar] [CrossRef]
- Hellier, A.K.; Brennan, F.P.; Carr, D.G. Weld toe SCF and stress distribution parametric equations for tension (membrane) loading. Adv. Mater. Res. 2014, 891. [Google Scholar] [CrossRef]
- Kiyak, Y.; Madia, M.; Zerbst, U. Extended parametric equations for weld toe stress concentration factors and through-thickness stress distributions in butt-welded plates subject to tensile and bending loading. Weld. World 2016, 60, 1–13. [Google Scholar] [CrossRef]
- Tateishi, K.; Hanibuchi, S. Extremely Low Cycle Fatigue ST Rength of Finished Welded Joints and its Simple Estimation. J. Japan Soc. Civil Eng., Ser. A1 (SE/EE) 2011, 67, 294–306. (In Japanese) [Google Scholar] [CrossRef] [Green Version]
- Tateishi, K.; Hanji, T.; Naruse, W.; Ito, I.; Choi, S. Fatigue strength evaluation for welded joints by newly developed local stress estimation method. Jpn. Sci. Tech. Agcy. (J. Struct. Engng. Ser. A) 2012, 58, 647–654. (In Japanese) [Google Scholar] [CrossRef]
- Dabiri, M.; Ghafouri, M.; Rohani Raftar, H.R.; Björk, T. Utilizing artificial neural networks for stress concentration factor calculation in butt welds. J. Constr. Steel Res. 2017, 138, 488–498. [Google Scholar] [CrossRef]
- Pachoud, A.J.; Manso, P.A.; Schleiss, A.J. New parametric equations to estimate notch stress concentration factors at butt welded joints modeling the weld profile with splines. Engng. Fail. Anal. 2017, 72, 11–24. [Google Scholar] [CrossRef]
- Berge, S.; Myhre, H. Fatigue strength of misaligned cruciform and butt joints. Norw. Marit. Res. 1977, 5, 29–39. [Google Scholar]
- Hobbacher, A. Recommendations for Fatigue Design of Welded Joints and Components, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Xing, S.; Dong, P. An analytical SCF solution method for joint misalignments and application in fatigue test data interpretation. Mar. Struct. 2016, 50, 143–161. [Google Scholar] [CrossRef]
- Ottersböck, M.; Leitner, M.; Stoschka, M. Impact of angular distortion on the fatigue performance of high-strength steel T-joints in as-welded and high frequency mechanical impact-treated condition. Metals 2018, 8, 302. [Google Scholar] [CrossRef] [Green Version]
- Abaqus Unified FEA. Available online: https://www.3ds.com/products-services/simulia/products/abaqus/ (accessed on 31 December 2019).
- Baumgartner, J.; Bruder, T. An efficient meshing approach for the calculation of notch stresses. Weld. World 2013, 57, 137–145. [Google Scholar] [CrossRef]















| Approach | Parametric Formula | Application Range |
|---|---|---|
| Ushirokawa and Nakayama [11] | Equation (A1) | ρ/ts: 0.025–0.35 δ/ts: 0.1–0.25 W/ts: 0.5 θ: 20°–50° |
| Kiyak et al. [19] | Equation (A2) | ρ/ts: 0.01–0.4 δ/ts: 0.075; 0.25 1 W/ts: 1.46 θ: 10°–60° |
| Pachoud et al. [23] | Equation (A3) | ts: 20; 35; 50 mm ρ: 0.4–1.9 mm δ/ts: 0.04–0.1 W/ts: 0.58–1.19 2 θ: 5°–30° |
| Coefficient | ||||||||
| Value | 1.398 | −0.144 | 0.715 | 1.650 | 0.322 | −2.233 | 2.319 | 0.526 |
| Coefficient | ||
| Value | 5.582 | −1.200 |
| Coefficient | ||||
| Value | 56,476.872 | 0.992 | −2.208 | −1.080 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Y.; Ma, R.; Tsutsumi, S. Parametric Formulae for Elastic Stress Concentration Factor at the Weld Toe of Distorted Butt-Welded Joints. Materials 2020, 13, 169. https://doi.org/10.3390/ma13010169
Luo Y, Ma R, Tsutsumi S. Parametric Formulae for Elastic Stress Concentration Factor at the Weld Toe of Distorted Butt-Welded Joints. Materials. 2020; 13(1):169. https://doi.org/10.3390/ma13010169
Chicago/Turabian StyleLuo, Yuxiao, Renle Ma, and Seiichiro Tsutsumi. 2020. "Parametric Formulae for Elastic Stress Concentration Factor at the Weld Toe of Distorted Butt-Welded Joints" Materials 13, no. 1: 169. https://doi.org/10.3390/ma13010169
APA StyleLuo, Y., Ma, R., & Tsutsumi, S. (2020). Parametric Formulae for Elastic Stress Concentration Factor at the Weld Toe of Distorted Butt-Welded Joints. Materials, 13(1), 169. https://doi.org/10.3390/ma13010169