Dynamics Studies of Nitrogen Interstitial in GaN from Ab Initio Calculations
Abstract
:1. Introduction
2. Methods
3. Results
3.1. Configurations of Ni
3.2. Migration of Ni
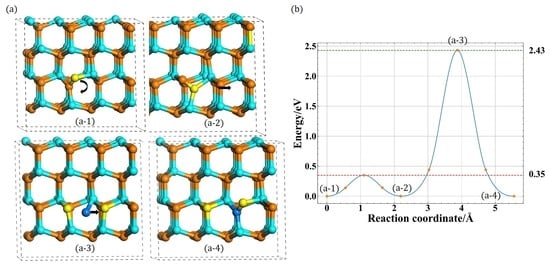
3.2.1. In-Plane Migration
3.2.2. Out-of-Plane Migration
3.3. Stability of Ni-VN Complex
3.4. Comparisons with the Experiments
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
Appendix A



References
- Li, Y.-C.; Chang, L.-B.; Chen, H.-J.; Yen, C.-Y.; Pan, K.-W.; Huang, B.-R.; Kuo, W.-Y.; Chow, L.; Zhou, D.; Popko, E. Phosphor-Free InGaN White Light Emitting Diodes Using Flip-Chip Technology. Materials 2017, 10, 432. [Google Scholar] [CrossRef] [PubMed]
- Polyakov, A.Y.; Lee, I.-H. Deep traps in GaN-based structures as affecting the performance of GaN devices. Mater. Sci. Eng. R Rep. 2015, 94, 1–56. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Yamada, H.; Yamada, T.; Takahashi, T.; Shimizu, M. Fabrication and Evaluation of N-Channel GaN Metal–Oxide–Semiconductor Field-Effect Transistors Based on Regrown and Implantation Methods. Materials 2020, 13, 899. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- He, H.; He, C.; Zhang, J.; Liao, W.; Zang, H.; Li, Y.; Liu, W.-B. Primary damage of 10 keV Ga PKA in bulk GaN material under different temperatures. Nucl. Eng. Technol. 2020, 52, 1537–1544. [Google Scholar] [CrossRef]
- Weaver, B.D.; Martin, P.A.; Boos, J.B.; Cress, C.D. Displacement Damage Effects in AlGaN/GaN High Electron Mobility Transistors. IEEE Trans. Nucl. Sci. 2012, 59, 3077–3080. [Google Scholar] [CrossRef]
- Costanzo, F.; Giofre, R.; Massari, A.; Feudale, M.; Suriani, A.; Limiti, E. A MMIC power amplifier in GaN on Si technology for next generation Q band high throughput satellite systems. Integration 2019, 68, 139–146. [Google Scholar] [CrossRef]
- Belabbas, I.; Chen, J.; Nouet, G. Electronic structure and metallization effects at threading dislocation cores in GaN. Comput. Mater. Sci. 2014, 90, 71–81. [Google Scholar] [CrossRef]
- Ene, V.L.; Dinescu, D.; Zai, I.; Djourelov, N.; Vasile, B.S.; Serban, A.B.; Leca, V.; Andronescu, E. Study of Edge and Screw Dislocation Density in GaN/Al2O3 Heterostructure. Materials 2019, 12, 42055. [Google Scholar] [CrossRef] [Green Version]
- Kanegae, K.; Fujikura, H.; Otoki, Y.; Konno, T.; Yoshida, T.; Horita, M.; Kimoto, T.; Suda, J. Deep-level transient spectroscopy studies of electron and hole traps in n-type GaN homoepitaxial layers grown by quartz-free hydride-vapor-phase epitaxy. Appl. Phys. Lett. 2019, 115, 012103. [Google Scholar] [CrossRef]
- Sunay, U.R.; E Zvanut, M.; Marbey, J.; Hill, S.; Leach, J.H.; Udwary, K. Small non-uniform basal crystal fields in HVPE free-standing GaN:Mg as evidenced by angular dependent and frequency-dependent EPR. J. Phys. Condens. Matter. 2019, 31, 345702. [Google Scholar] [CrossRef]
- Van Bardeleben, H.J.; Cantin, J.-L.; Gerstmann, U.; Scholle, A.; Greulich-Weber, S.; Rauls, E.; Landmann, M.; Schmidt, W.G.; Gentils, A.; Botsoa, J.; et al. Identification of the Nitrogen Split Interstitial (N-N)N in GaN. Phys. Rev. Lett. 2012, 109, 206402. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, F.; Bylaska, E.J.; Weber, W.J. Intrinsic Defect Properties in GaN Calculated by Ab Initio and Empirical Potential Methods. Phys. Rev. B 2004, 70, 245208. [Google Scholar] [CrossRef]
- Lyons, J.L.; Van de Walle, C.G. Computationally predicted energies and properties of defects in GaN. NPJ Comput. Mater. 2017, 3, 180. [Google Scholar] [CrossRef]
- Gao, Y.; Sun, D.; Jiang, X.; Zhao, J. Point defects in group III nitrides: A comparative first-principles study. J. Appl. Phys. 2019, 125, 215705. [Google Scholar] [CrossRef]
- Matsubara, M.; Bellotti, E. A first-principles study of carbon-related energy levels in GaN: I. Complexes formed by substitutional/interstitial carbons and gallium/nitrogen vacancies. J. Appl. Phys. 2017, 121, 195701. [Google Scholar] [CrossRef] [Green Version]
- Xie, Z.; Sui, Y.; Buckeridge, J.; A Catlow, C.R.; Keal, T.W.; Sherwood, P.; Walsh, A.; Farrow, M.R.; Scanlon, D.O.; Woodley, S.M.; et al. Donor and acceptor characteristics of native point defects in GaN. J. Phys. D Appl. Phys. 2019, 52, 335104. [Google Scholar] [CrossRef] [Green Version]
- Diallo, I.C.; Demchenko, D.O. Native Point Defects in GaN: A Hybrid-Functional Study. Phys. Rev. Appl. 2016, 6, 064002. [Google Scholar] [CrossRef] [Green Version]
- Kyrtsos, A.; Matsubara, M.; Bellotti, E. Migration mechanisms and diffusion barriers of carbon and native point defects in GaN. Phys. Rev. B 2016, 93, 245201. [Google Scholar] [CrossRef] [Green Version]
- Limpijumnong, S.; Van de Walle, C.G. Diffusivity of native defects in GaN. Phys. Rev. B 2004, 69, 035207. [Google Scholar] [CrossRef]
- Kresse, G.; Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kresse, G.; Joubert, D. From ultrasoft pseudopotentials to the projector augmented-wave method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Henkelman, G.; Uberuaga, B.P.; Jónsson, H. A climbing image nudged elastic band method for finding saddle points and minimum energy paths. J. Chem. Phys. 2000, 113, 9901–9904. [Google Scholar] [CrossRef] [Green Version]
- Henkelman, G.; Jónsson, H. A dimer method for finding saddle points on high dimensional potential surfaces using only first derivatives. J. Chem. Phys. 1999, 111, 7010–7022. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 11002. [Google Scholar] [CrossRef] [Green Version]
- Schulz, H.; Thiemann, K. Crystal structure refinement of AlN and GaN. Solid State Commun. 1977, 23, 815–819. [Google Scholar] [CrossRef]
- Freysoldt, C.; Neugebauer, J.; Van De Walle, C.G. Fully Ab Initio Finite-Size Corrections for Charged-Defect Supercell Calculations. Phys. Rev. Lett. 2009, 102, 016402. [Google Scholar] [CrossRef] [Green Version]
- Chung, J.W.; Hoke, W.; Chumbes, E.; Palacios, T. AlGaN/GaN Hemt with 300-Ghz Fmax. IEEE Electron. Device Lett. 2010, 31, 195–197. [Google Scholar] [CrossRef]
- Weichuan, X.; Liu, Z.; Qiu, H.; Ranjan, K.; Palacios, T. Inaln/Gan Hemts on Si with High fT of 250 Ghz. IEEE Electron. Device Lett. 2017, 39, 75–78. [Google Scholar]
- Tang, W.; Sanville, E.; Henkelman, G. A grid-based Bader analysis algorithm without lattice bias. J. Phys. Condens. Matter 2009, 21, 084204. [Google Scholar] [CrossRef]
- Henkelman, G.; Arnaldsson, A.; Jónsson, H. A fast and robust algorithm for Bader decomposition of charge density. Comput. Mater. Sci. 2006, 36, 354–360. [Google Scholar] [CrossRef]
- Beck, M.J.; Tsetseris, L.; Pantelides, S.T. Stability and Dynamics of Frenkel Pairs in Si. Phys. Rev. Lett. 2007, 99, 215503. [Google Scholar] [CrossRef] [PubMed]
- Dippong, T.; Levei, E.A.; Cadar, O.; Goga, F.; Toloman, D.; Borodi, G. Thermal behavior of Ni, Co and Fe succinates embedded in silica matrix. J. Therm. Anal. Calorim. 2019, 136, 1587–1596. [Google Scholar] [CrossRef]
- Gerstmann, U.; Rauls, E.; Frauenheim, T.; Overhof, H. Formation and annealing of nitrogen-related complexes in SiC. Phys. Rev. B 2003, 67, 205202. [Google Scholar] [CrossRef]
- Sahoo, B.K.; Sahoo, S.K.; Sahoo, S. Macroscopic polarization and thermal conductivity of GaN. J. Phys. Chem. Solids 2013, 74, 1669–1671. [Google Scholar] [CrossRef]








| Charge State | dN-N (Å) | Parameter c | ||
|---|---|---|---|---|
| This Work | Other Work | Other Work (%) | ||
| 3 | 1.15 | 1.12 a 1.11 b | 2.61 a 3.48 b | 1.50 |
| 2 | 1.20 | 1.18 a | 1.67 a | 1.51 |
| 1 | 1.27 | 1.25 a | 1.57 a | 1.55 |
| 0 | 1.35 | 1.34 a | 0.74 a | 1.75 |
| −1 | 1.44 | 1.45 a 1.41 b | 0.69 a 2.08 b | 2.27 |
| Charge State | Rotation Barrier/eV | In/eV(upward/downward) | Out/eV | In/eV | Out/eV |
|---|---|---|---|---|---|
| −1 | 0.33 | 1.80/1.80 | 1.87 | 1.9 a, 1.6 b | 1.9 a, 1.6 b |
| 0 | 0.35 | 2.34/2.43 | 2.40 | 2.4 a, 2.4 b, 2.33 c | 2.4 a, 2.4 b |
| 1 | 0.27 | 2.48/2.52 | 2.18 | 2.2 a, 2.1 b | 2.1 a, 2.1 b |
| 2 | 0.24 | 1.98/2.08 | 2.13 | 2.1 a, 2.5 b | 2.2 a, 2.5 b |
| 3 | 0.23 | 1.57/1.26 | 2.13 | 2.1 a, 1.4 b | 1.7 a, 1.4 b |
| Defect Type | Charge State | Bond Length/Å |
|---|---|---|
| Ni-VN | +3 | 1.21 |
| +2 | 1.26 | |
| +1 | 1.34 | |
| 0 | 1.44 |
| Defect Type | Charge State | Ni-VN (Ni/VN) | Isolated One (Ni/VN) |
|---|---|---|---|
| Bader Charge(|e|) | 3 | 0.51/1.23 | 0.21/1.43 |
| 2 | 0.67/1.21 | 0.44/1.28 | |
| 1 | 0.84/1.19 | 0.66/1.21 | |
| 0 | 1.04/1.22 | 0.87/1.15 | |
| −1 | – | 1.05/1.07 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, H.; Liu, W.; Zhang, P.; Liao, W.; Tong, D.; Yang, L.; He, C.; Zang, H.; Zong, H. Dynamics Studies of Nitrogen Interstitial in GaN from Ab Initio Calculations. Materials 2020, 13, 3627. https://doi.org/10.3390/ma13163627
He H, Liu W, Zhang P, Liao W, Tong D, Yang L, He C, Zang H, Zong H. Dynamics Studies of Nitrogen Interstitial in GaN from Ab Initio Calculations. Materials. 2020; 13(16):3627. https://doi.org/10.3390/ma13163627
Chicago/Turabian StyleHe, Huan, Wenbo Liu, Pengbo Zhang, Wenlong Liao, Dayin Tong, Lin Yang, Chaohui He, Hang Zang, and Hongxiang Zong. 2020. "Dynamics Studies of Nitrogen Interstitial in GaN from Ab Initio Calculations" Materials 13, no. 16: 3627. https://doi.org/10.3390/ma13163627
APA StyleHe, H., Liu, W., Zhang, P., Liao, W., Tong, D., Yang, L., He, C., Zang, H., & Zong, H. (2020). Dynamics Studies of Nitrogen Interstitial in GaN from Ab Initio Calculations. Materials, 13(16), 3627. https://doi.org/10.3390/ma13163627