Laser Powder Bed Fusion (LPBF) of In718 and the Impact of Pre-Heating at 500 and 1000 °C: Operando Study
Abstract
:1. Introduction
2. Materials and Methods
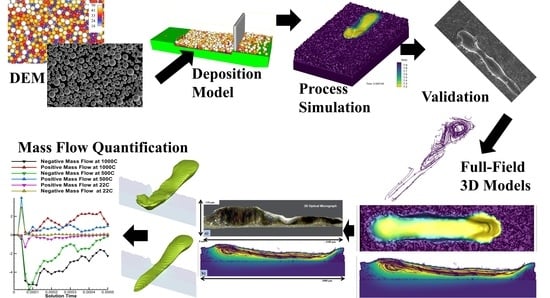
2.1. Powder Bed Modeling
2.2. Modeling of Powder Bed Deposition Process
2.3. Modeling of Thermophysical Properties
2.4. Numerical Model
2.5. Configuration of the Modeling Environment and Variables
2.6. Experimental Procedure
3. Results and Discussion
4. Conclusions
- The melted flow patterns in every region of the entire melt pool have shown a fairly complicated flow pattern due to the interaction of several driving factors. We measured and derived equation a drop in flow velocity from the depression region to the melt pool rear region.
- The propelling factors for various melt flow variations were studied. The Marangoni effect is responsible for the circulation flow from a low surface tension to a high surface tension region on the melted surface. The fluid movement all across depression-zone sidewalls is dominated by evaporation. Hydraulic pressure propels fluid movement from an area of high pressures to a low-pressure area. Buoyance pressure is responsible for fluid convection between low- and high-density regions.
- Only at laser irradiating region of its melt pool, the powerful major factors are recoil liquid momentum and heat convection; just at rear of the melt pool, the dominant major factors have been determined for being high surface tension and the thermal conductivity, respectively.
- Throughout this study, modeling shows an increase in pre-heating level across the melt pool variability (wide, height, and duration).
- greater pre-heating temperature create a melt pool having greater depth and relatively dimension. In modeling, a front sidewall inclination of irradiating region increases with pre-heating temperatures, indicating more laser drill force. Increasing the temperature degree increases penetration.
- As the solidification speed rises, the melting period tends to become shorter. Due to increased retribution force and fluid suppressing, the reversed melt flow from both the laser center region and Marangoni power is not possible leading to higher residual stresses. Lower pre levels typically have faster movement. At higher pre-heating levels the residual stresses can be reduced as the melt pool has more time to release the pressures.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kok, Y.; Tan, X.P.; Wang, P.; Nai, M.L.S.; Loh, N.H.; Liu, E.; Tor, S.B. Anisotropy and heterogeneity of microstructure and mechanical properties in metal additive manufacturing: A critical review. Mater. Des. 2018, 139, 565–586. [Google Scholar] [CrossRef]
- Guo, N.; Leu, M.C. Additive manufacturing: Technology, applications and research needs. Front. Mech. Eng. 2013, 8, 215–243. [Google Scholar] [CrossRef]
- Tiwari, S.K.; Pande, S.; Agrawal, S.; Bobade, S.M. Selection of selective laser sintering materials for different applications. Rapid Prototyp. J. 2015, 21, 630–648. [Google Scholar] [CrossRef]
- Liu, F.H. Synthesis of bioceramic scaffolds for bone tissue engineering by rapid prototyping technique. J. Sol-Gel Sci. Technol. 2012, 64, 704–710. [Google Scholar] [CrossRef]
- Ur Rehman, A.; Sglavo, V.M. 3D printing of geopolymer-based concrete for building applications. Rapid Prototyp. J. 2020, 26, 1783–1788. [Google Scholar] [CrossRef]
- Ur Rehman, A.; Sglavo, V.M. 3D printing of Portland cement-containing bodies. Rapid Prototyp. J. 2021. ahead-of-print. [Google Scholar] [CrossRef]
- Mahmood, M.A.; Popescu, A.C.; Mihailescu, I.N. Metal matrix composites synthesized by laser-melting deposition: A review. Materials 2020, 13, 2593. [Google Scholar] [CrossRef]
- Mahmood, M.A.; Popescu, A.C.; Oane, M.; Channa, A.; Mihai, S.; Ristoscu, C.; Mihailescu, I.N. Bridging the analytical and artificial neural network models for keyhole formation with experimental verification in laser melting deposition: A novel approach. Results Phys. 2021, 26, 104440. [Google Scholar] [CrossRef]
- Körner, C. Additive manufacturing of metallic components by selective electron beam melting—A review. Int. Mater. Rev. 2016, 61, 361–377. [Google Scholar]
- Fayazfar, H.; Salarian, M.; Rogalsky, A.; Sarker, D.; Russo, P.; Paserin, V.; Toyserkani, E. A critical review of powder-based additive manufacturing of ferrous alloys: Process parameters, microstructure and mechanical properties. Mater. Des. 2018, 144, 98–128. [Google Scholar] [CrossRef]
- Ur Rehman, A. Additive Manufacturing of Ceramic Materials and Combinations with New Laser Strategies. Master’s Thesis, Nanjing University of Science and Technology, Nanjing, Jiangsu, China, 2017. [Google Scholar]
- Everton, S.K.; Hirsch, M.; Stavroulakis, P.I.; Leach, R.K.; Clare, A.T. Review of in-situ process monitoring and in-situ metrology for metal additive manufacturing. Mater. Des. 2016, 95, 431–445. [Google Scholar] [CrossRef]
- Sing, S.L.; An, J.; Yeong, W.Y.; Wiria, F.E. Laser and electron-beam powder-bed additive manufacturing of metallic implants: A review on processes, materials and designs. J. Orthop. Res. 2016, 34, 369–385. [Google Scholar] [CrossRef]
- Olakanmi, E.O.; Cochrane, R.F.; Dalgarno, K.W. A review on selective laser sintering/melting (SLS/SLM) of aluminium alloy powders: Processing, microstructure, and properties. Prog. Mater. Sci. 2015, 74, 401–477. [Google Scholar] [CrossRef]
- Ansari, P.; Rehman, A.U.; Pitir, F.; Veziroglu, S.; Mishra, Y.K.; Aktas, O.C.; Salamci, M.U. Selective Laser Melting of 316L Austenitic Stainless Steel: Detailed Process Understanding Using Multiphysics Simulation and Experimentation. Metals 2021, 11, 1076. [Google Scholar] [CrossRef]
- Ullah, A.; Wu, H.; Ur Rehman, A.; Zhu, Y.; Liu, T.; Zhang, K. Influence of laser parameters and Ti content on the surface morphology of L-PBF fabricated Titania. Rapid Prototyp. J. 2021, 27, 71–80. [Google Scholar] [CrossRef]
- Bidare, P.; Maier, R.R.J.; Beck, R.J.; Shephard, J.D.; Moore, A.J. An open-architecture metal powder bed fusion system for in-situ process measurements. Addit. Manuf. 2017, 16, 177–185. [Google Scholar] [CrossRef]
- Yamada, T.; Shobu, T.; Nishimura, A.; Yonemoto, Y.; Yamashita, S.; Muramatsu, T. In-situ X-ray observation of molten pool depth during laser micro welding. J. Laser Micro Nanoeng. 2012, 7, 244–248. [Google Scholar] [CrossRef] [Green Version]
- Scipioni Bertoli, U.; Guss, G.; Wu, S.; Matthews, M.J.; Schoenung, J.M. In-situ characterization of laser-powder interaction and cooling rates through high-speed imaging of powder bed fusion additive manufacturing. Mater. Des. 2017, 135, 385–396. [Google Scholar] [CrossRef]
- Repossini, G.; Laguzza, V.; Grasso, M.; Colosimo, B.M. On the use of spatter signature for in-situ monitoring of Laser Powder Bed Fusion. Addit. Manuf. 2017, 16, 35–48. [Google Scholar] [CrossRef]
- King, W.; Anderson, A.T.; Ferencz, R.M.; Hodge, N.E.; Kamath, C.; Khairallah, S.A. Overview of modelling and simulation of metal powder bed fusion process at Lawrence Livermore National Laboratory. Mater. Sci. Technol. 2015, 31, 957–968. [Google Scholar] [CrossRef]
- Le, T.-N.; Lo, Y.-L.; Lin, Z.-H. Numerical simulation and experimental validation of melting and solidification process in selective laser melting of IN718 alloy. Addit. Manuf. 2020, 36, 101519. [Google Scholar] [CrossRef]
- Rahman, M.S.; Schilling, P.J.; Herrington, P.D.; Chakravarty, U.K. A Comparison of the Thermo-Fluid Properties of Ti-6Al-4V Melt Pools Formed by Laser and Electron-Beam Powder-Bed Fusion Processes. J. Eng. Mater. Technol. 2021, 143. [Google Scholar] [CrossRef]
- Gong, H.; Rafi, K.; Gu, H.; Starr, T.; Stucker, B. Analysis of defect generation in Ti-6Al-4V parts made using powder bed fusion additive manufacturing processes. Addit. Manuf. 2014, 1, 87–98. [Google Scholar] [CrossRef]
- DebRoy, T.; Wei, H.L.; Zuback, J.S.; Mukherjee, T.; Elmer, J.W.; Milewski, J.O.; Beese, A.M.; Wilson-Heid, A.; De, A.; Zhang, W. Additive manufacturing of metallic components—Process, structure and properties. Prog. Mater. Sci. 2018, 92, 112–224. [Google Scholar]
- Frazier, W.E. Metal additive manufacturing: A review. J. Mater. Eng. Perform. 2014, 23, 1917–1928. [Google Scholar]
- Guo, Q.; Zhao, C.; Qu, M.; Xiong, L.; Hojjatzadeh, S.M.H.; Escano, L.I.; Parab, N.D.; Fezzaa, K.; Sun, T.; Chen, L. In-situ full-field mapping of melt flow dynamics in laser metal additive manufacturing. Addit. Manuf. 2020, 31, 100939. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, C.; Qu, M.; Xiong, L.; Escano, L.I.; Hojjatzadeh, S.M.H.; Parab, N.D.; Fezzaa, K.; Everhart, W.; Sun, T.; et al. In-situ characterization and quantification of melt pool variation under constant input energy density in laser powder bed fusion additive manufacturing process. Addit. Manuf. 2019, 28, 600–609. [Google Scholar] [CrossRef]
- Leung, C.L.A.; Marussi, S.; Atwood, R.C.; Towrie, M.; Withers, P.J.; Lee, P.D. In situ X-ray imaging of defect and molten pool dynamics in laser additive manufacturing. Nat. Commun. 2018, 9, 1355. [Google Scholar] [CrossRef] [Green Version]
- Kawahito, Y.; Mizutani, M.; Katayama, S. Elucidation of high-power fibre laser welding phenomena of stainless steel and effect of factors on weld geometry. J. Phys. D Appl. Phys. 2007, 40, 5854–5859. [Google Scholar] [CrossRef]
- Kawahito, Y.; Uemura, Y.; Doi, Y.; Mizutani, M.; Nishimoto, K.; Kawakami, H.; Tanaka, M.; Fujii, H.; Nakata, K.; Katayama, S. Elucidation of the effect of welding speed on melt flows in high-brightness and high-power laser welding of stainless steel on basis of three-dimensional X-ray transmission in situ observation. Weld. Int. 2017, 31, 206–213. [Google Scholar] [CrossRef]
- Olakanmi, E.O. Selective laser sintering/melting (SLS/SLM) of pure Al, Al-Mg, and Al-Si powders: Effect of processing conditions and powder properties. J. Mater. Process. Technol. 2013, 213, 1387–1405. [Google Scholar] [CrossRef]
- Yadroitsev, I.; Krakhmalev, P.; Yadroitsava, I.; Johansson, S.; Smurov, I. Energy input effect on morphology and microstructure of selective laser melting single track from metallic powder. J. Mater. Process. Technol. 2013, 213, 606–613. [Google Scholar] [CrossRef]
- Amato, K.N.; Gaytan, S.M.; Murr, L.E.; Martinez, E.; Shindo, P.W.; Hernandez, J.; Collins, S.; Medina, F. Microstructures and mechanical behavior of Inconel 718 fabricated by selective laser melting. Acta Mater. 2012, 60, 2229–2239. [Google Scholar] [CrossRef]
- Ansari, P.; Salamci, M.U. On the selective laser melting based additive manufacturing of AlSi10Mg: The process parameter investigation through multiphysics simulation and experimental validation. J. Alloys Compd. 2022, 890, 161873. [Google Scholar] [CrossRef]
- Nasab, M.H.; Gastaldi, D.; Lecis, N.F.; Vedani, M. On morphological surface features of the parts printed by selective laser melting (SLM). Addit. Manuf. 2018, 24, 373–377. [Google Scholar] [CrossRef]
- Simonelli, M.; Tuck, C.; Aboulkhair, N.T.; Maskery, I.; Ashcroft, I.; Wildman, R.D.; Hague, R. A Study on the Laser Spatter and the Oxidation Reactions During Selective Laser Melting of 316L Stainless Steel, Al-Si10-Mg, and Ti-6Al-4V. Metall. Mater. Trans. A Phys. Metall. Mater. Sci. 2015, 46, 3842–3851. [Google Scholar] [CrossRef]
- Liu, Y.; Yang, Y.; Mai, S.; Wang, D.; Song, C. Investigation into spatter behavior during selective laser melting of AISI 316L stainless steel powder. Mater. Des. 2015, 87, 797–806. [Google Scholar] [CrossRef]
- Herzog, D.; Seyda, V.; Wycisk, E.; Emmelmann, C. Additive manufacturing of metals. Acta Mater. 2016, 117, 371–392. [Google Scholar] [CrossRef]
- Hebert, R.J. Viewpoint: Metallurgical aspects of powder bed metal additive manufacturing. J. Mater. Sci. 2016, 51, 1165–1175. [Google Scholar] [CrossRef]
- Zhou, Q.; Hayat, M.D.; Chen, G.; Cai, S.; Qu, X.; Tang, H.; Cao, P. Selective electron beam melting of NiTi: Microstructure, phase transformation and mechanical properties. Mater. Sci. Eng. A 2019, 744, 290–298. [Google Scholar] [CrossRef]
- Kamath, C.; El-Dasher, B.; Gallegos, G.F.; King, W.E.; Sisto, A. Density of additively-manufactured, 316L SS parts using laser powder-bed fusion at powers up to 400 W. Int. J. Adv. Manuf. Technol. 2014, 74, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Sohail, M.; Han, S.W.; Na, S.J.; Gumenyuk, A.; Rethmeier, M. Characteristics of weld pool behavior in laser welding with various power inputs. Weld. World 2014, 58, 269–277. [Google Scholar] [CrossRef]
- Matsunawa, A.; Kim, J.-D.; Seto, N.; Mizutani, M.; Katayama, S. Dynamics of keyhole and molten pool in laser welding. J. Laser Appl. 1998, 10, 247–254. [Google Scholar] [CrossRef]
- Rauniyar, S.K.; Chou, K. Melt Pool Analysis and Mesoscale Simulation of Laser Powder Bed Fusion Process (L-PBF) with Ti-6Al-4V Powder Particles. Jom 2019, 71, 938–945. [Google Scholar] [CrossRef]
- Shrestha, S.; Rauniyar, S.; Chou, K. Thermo-Fluid Modeling of Selective Laser Melting: Single-Track Formation Incorporating Metallic Powder. J. Mater. Eng. Perform. 2019, 28, 611–619. [Google Scholar] [CrossRef]
- Wolff, S.J.; Wu, H.; Parab, N.; Zhao, C.; Ehmann, K.F.; Sun, T.; Cao, J. In-situ high-speed X-ray imaging of piezo-driven directed energy deposition additive manufacturing. Sci. Rep. 2019, 9, 962. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gan, Z.; Liu, H.; Li, S.; He, X.; Yu, G. Modeling of thermal behavior and mass transport in multi-layer laser additive manufacturing of Ni-based alloy on cast iron. Int. J. Heat Mass Transf. 2017, 111, 709–722. [Google Scholar] [CrossRef] [Green Version]
- Tian, Y.; Yang, L.; Zhao, D.; Huang, Y.; Pan, J. Numerical analysis of powder bed generation and single track forming for selective laser melting of SS316L stainless steel. J. Manuf. Process. 2020, 58, 964–974. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.M.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. In Additive Manufacturing Handbook Product Development for the Defense Industry; CRC Press: Boca Raton, FL, USA, 2017; pp. 613–628. [Google Scholar] [CrossRef]
- Khairallah, S.A.; Anderson, A.T.; Rubenchik, A.M.; King, W.E. Laser powder-bed fusion additive manufacturing: Physics of complex melt flow and formation mechanisms of pores, spatter, and denudation zones. Acta Mater. 2016, 108, 36–45. [Google Scholar] [CrossRef] [Green Version]
- Peng, J.; Zhang, W.; Wang, X.; Guo, G.; Zhang, F. Numerical simulation of effect of filler wire melting and filling mode on molten pool in laser welding. Hongwai yu Jiguang Gongcheng/Infrared Laser Eng. 2018, 47, 306005. [Google Scholar] [CrossRef]
- Xia, M.; Gu, D.; Yu, G.; Dai, D.; Chen, H.; Shi, Q. Porosity evolution and its thermodynamic mechanism of randomly packed powder-bed during selective laser melting of Inconel 718 alloy. Int. J. Mach. Tools Manuf. 2017, 116, 96–106. [Google Scholar] [CrossRef]
- Aucott, L.; Dong, H.; Mirihanage, W.; Atwood, R.; Kidess, A.; Gao, S.; Wen, S.; Marsden, J.; Feng, S.; Tong, M.; et al. Revealing internal flow behaviour in arc welding and additive manufacturing of metals. Nat. Commun. 2018, 9, 5414. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hojjatzadeh, S.M.H.; Parab, N.D.; Yan, W.; Guo, Q.; Xiong, L.; Zhao, C.; Qu, M.; Escano, L.I.; Xiao, X.; Fezzaa, K.; et al. Pore elimination mechanisms during 3D printing of metals. Nat. Commun. 2019, 10, 3088. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ur Rehman, A.; Pitir, F.; Salamci, M.U. Full-Field Mapping and Flow Quantification of Melt Pool Dynamics in Laser Powder Bed Fusion of SS316L. Materials 2021, 14, 6264. [Google Scholar] [CrossRef]
- Ur Rehman, A.; Mahmood, M.A.; Pitir, F.; Salamci, M.U.; Popescu, A.C.; Mihailescu, I.N. Mesoscopic Computational Fluid Dynamics Modelling for the Laser-Melting Deposition of AISI 304 Stainless Steel Single Tracks with Experimental Correlation: A Novel Study. Metals 2021, 11, 1569. [Google Scholar] [CrossRef]
- Denlinger, E.R.; Irwin, J.; Michaleris, P. Thermomechanical modeling of additive manufacturing large parts. J. Manuf. Sci. Eng. Trans. ASME 2014, 136, 061007. [Google Scholar] [CrossRef]
- Li, C.; Gouge, M.F.; Denlinger, E.R.; Irwin, J.E.; Michaleris, P. Estimation of part-to-powder heat losses as surface convection in laser powder bed fusion. Addit. Manuf. 2019, 26, 258–269. [Google Scholar] [CrossRef]
- Agarwala, M.; Bourell, D.; Beaman, J.; Marcus, H.; Barlow, J. Direct selective laser sintering of metals. Rapid Prototyp. J. 1995, 1, 26–36. [Google Scholar] [CrossRef]
- Aboulkhair, N.T.; Everitt, N.M.; Ashcroft, I.; Tuck, C. Reducing porosity in AlSi10Mg parts processed by selective laser melting. Addit. Manuf. 2014, 1, 77–86. [Google Scholar] [CrossRef]
- Demir, A.G.; Previtali, B. Investigation of remelting and preheating in SLM of 18Ni300 maraging steel as corrective and preventive measures for porosity reduction. Int. J. Adv. Manuf. Technol. 2017, 93, 2697–2709. [Google Scholar] [CrossRef]
- Colopi, M.; Demir, A.G.; Caprio, L.; Previtali, B. Limits and solutions in processing pure Cu via selective laser melting using a high-power single-mode fiber laser. Int. J. Adv. Manuf. Technol. 2019, 104, 2473–2486. [Google Scholar] [CrossRef]
- Wilkes, J.; Hagedorn, Y.C.; Meiners, W.; Wissenbach, K. Additive manufacturing of ZrO2-Al2O3 ceramic components by selective laser melting. Rapid Prototyp. J. 2013, 19, 51–57. [Google Scholar] [CrossRef]
- Kempen, K.; Vrancken, B.; Buls, S.; Thijs, L.; Van Humbeeck, J.; Kruth, J.P. Selective Laser Melting of Crack-Free High Density M2 High Speed Steel Parts by Baseplate Preheating. J. Manuf. Sci. Eng. Trans. ASME 2014, 136, 061026. [Google Scholar] [CrossRef]
- Ali, H.; Ma, L.; Ghadbeigi, H.; Mumtaz, K. In-situ residual stress reduction, martensitic decomposition and mechanical properties enhancement through high temperature powder bed pre-heating of Selective Laser Melted Ti6Al4V. Mater. Sci. Eng. A 2017, 695, 211–220. [Google Scholar] [CrossRef]
- Gussone, J.; Hagedorn, Y.C.; Gherekhloo, H.; Kasperovich, G.; Merzouk, T.; Hausmann, J. Microstructure of γ-titanium aluminide processed by selected laser melting at elevated temperatures. Intermetallics 2015, 66, 133–140. [Google Scholar] [CrossRef]
- Ding, C.; Cui, X.; Jiao, J.; Zhu, P. Effects of substrate preheating temperatures on the microstructure, properties, and residual stress of 12CrNi2 prepared by laser cladding deposition technique. Materials 2018, 11, 2401. [Google Scholar] [CrossRef] [Green Version]
- Buchbinder, D.; Meiners, W.; Pirch, N.; Wissenbach, K.; Schrage, J. Investigation on reducing distortion by preheating during manufacture of aluminum components using selective laser melting. J. Laser Appl. 2014, 26, 012004. [Google Scholar] [CrossRef]
- Kruth, J.P.; Deckers, J.; Yasa, E.; Wauthlé, R. Assessing and comparing influencing factors of residual stresses in selective laser melting using a novel analysis method. Proc. Inst. Mech. Eng. Part B J. Eng. Manuf. 2012, 226, 980–991. [Google Scholar] [CrossRef]
- Leung, C.L.A.; Tosi, R.; Muzangaza, E.; Nonni, S.; Withers, P.J.; Lee, P.D. Effect of preheating on the thermal, microstructural and mechanical properties of selective electron beam melted Ti-6Al-4V components. Mater. Des. 2019, 174, 107792. [Google Scholar] [CrossRef]
- Zhang, K.; Liu, T.; Liao, W.; Zhang, C.; Yan, Y.; Du, D. Influence of laser parameters on the surface morphology of slurry-based Al2O3 parts produced through selective laser melting. Rapid Prototyp. J. 2018, 24, 333–341. [Google Scholar] [CrossRef]
- Antonsson, T.; Fredriksson, H. The effect of cooling rate on the solidification of INCONEL 718. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2005, 36, 85–96. [Google Scholar] [CrossRef]
- Wang, Z.; Guan, K.; Gao, M.; Li, X.; Chen, X.; Zeng, X. The microstructure and mechanical properties of deposited-IN718 by selective laser melting. J. Alloys Compd. 2012, 513, 518–523. [Google Scholar] [CrossRef]
- Gruber, K.; Smolina, I.; Kasprowicz, M.; Kurzynowski, T. Evaluation of Inconel 718 Metallic Powder to Optimize the Reuse of Powder and to Improve the Performance and Sustainability of the Laser Powder Bed Fusion (LPBF) Process. Materials 2021, 14, 1538. [Google Scholar] [CrossRef]
- Cleary, P.W.; Sawley, M.L. DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge. Appl. Math. Model. 2002, 26, 89–111. [Google Scholar] [CrossRef]
- Parteli, E.J.R.; Pöschel, T. Particle-based simulation of powder application in additive manufacturing. Powder Technol. 2016, 288, 96–102. [Google Scholar] [CrossRef]
- Cao, L. Numerical simulation of the impact of laying powder on selective laser melting single-pass formation. Int. J. Heat Mass Transf. 2019, 141, 1036–1048. [Google Scholar] [CrossRef]
- Juan, J.V.; Peter, N.Q. Thermophysical Properties; ASM Handbook Committee: Materials Park, OH, USA, 2018; Volume 17. [Google Scholar]
- Lee, Y.S.; Zhang, W. Modeling of heat transfer, fluid flow and solidification microstructure of nickel-base superalloy fabricated by laser powder bed fusion. Addit. Manuf. 2016, 12, 178–188. [Google Scholar] [CrossRef] [Green Version]
- Tang, M.; Pistorius, P.C.; Beuth, J.L. Prediction of lack-of-fusion porosity for powder bed fusion. Addit. Manuf. 2017, 14, 39–48. [Google Scholar] [CrossRef]
- Promoppatum, P.; Yao, S.C.; Pistorius, P.C.; Rollett, A.D. A Comprehensive Comparison of the Analytical and Numerical Prediction of the Thermal History and Solidification Microstructure of Inconel 718 Products Made by Laser Powder-Bed Fusion. Engineering 2017, 3, 685–694. [Google Scholar] [CrossRef]
- Rosenthal, D. Mathematical Theory of Heat Distribution During Welding and Cutting. Weld. J. 1941, 20, 220–234. [Google Scholar]
- Chen, Q.; Zhao, Y.Y.; Strayer, S.; Zhao, Y.Y.; Aoyagi, K.; Koizumi, Y.; Chiba, A.; Xiong, W.; To, A.C. Elucidating the Effect of Preheating Temperature on Melt Pool Morphology Variation in Inconel 718 Laser Powder Bed Fusion via Simulation and Experiment. Available online: https://www.sciencedirect.com/science/article/pii/S2214860420310149#bb8 (accessed on 30 April 2021).
- Paul, A.; Debroy, T. Free surface flow and heat transfer in conduction mode laser welding. Metall. Trans. B 1988, 19, 851–858. [Google Scholar] [CrossRef]
- Peng, J.; Hu, S.; Wang, X.; Wang, J.; Zhang, F. Effect of Filler Metal on Three-Dimensional Transient Behavior of Keyholes and Molten Pools in Laser Welding. Zhongguo Jiguang/Chinese J. Lasers 2018, 45, 0102003. [Google Scholar] [CrossRef]
- Abderrazak, K.; Bannour, S.; Mhiri, H.; Lepalec, G.; Autric, M. Numerical and experimental study of molten pool formation during continuous laser welding of AZ91 magnesium alloy. Comput. Mater. Sci. 2009, 44, 858–866. [Google Scholar] [CrossRef]
- Tenner, F.; Berg, B.; Brock, C.; Klämpfl, F.; Schmidt, M. Experimental approach for quantification of fluid dynamics in laser metal welding. J. Laser Appl. 2015, 27, S29003. [Google Scholar] [CrossRef]
- Eriksson, I.; Powell, J.; Kaplan, A.F.H. Melt behavior on the keyhole front during high speed laser welding. Opt. Lasers Eng. 2013, 51, 735–740. [Google Scholar] [CrossRef] [Green Version]
- Nakamura, H.; Kawahito, Y.; Nishimoto, K.; Katayama, S. Elucidation of melt flows and spatter formation mechanisms during high power laser welding of pure titanium. J. Laser Appl. 2015, 27, 032012. [Google Scholar] [CrossRef]
- Bidare, P.; Bitharas, I.; Ward, R.M.; Attallah, M.M.; Moore, A.J. Fluid and particle dynamics in laser powder bed fusion. Acta Mater. 2018, 142, 107–120. [Google Scholar] [CrossRef]
- Matsunawa, A.; Seto, N.; Mizutani, M.; Katayama, S. Liquid Motion in Keyhole Laser Welding; Laser Institute of America: Orlando, FL, USA, 2018; pp. G151–G160. [Google Scholar]
- Chang, B.; Allen, C.; Blackburn, J.; Hilton, P.; Du, D. Fluid Flow Characteristics and Porosity Behavior in Full Penetration Laser Welding of a Titanium Alloy. Metall. Mater. Trans. B Process Metall. Mater. Process. Sci. 2015, 46, 906–918. [Google Scholar] [CrossRef]
- Peng, J.; Li, L.; Lin, S.; Zhang, F.; Pan, Q.; Katayama, S. High-Speed X-Ray Transmission and Numerical Study of Melt Flows inside the Molten Pool during Laser Welding of Aluminum Alloy. Math. Probl. Eng. 2016, 2016, 1409872. [Google Scholar] [CrossRef] [Green Version]
- Kawahito, Y.; Nakada, K.; Uemura, Y.; Mizutani, M.; Nishimoto, K.; Kawakami, H.; Katayama, S. Relationship between melt flows based on three-dimensional X-ray transmission in situ observation and spatter reduction by angle of incidence and defocussing distance in high-power laser welding of stainless steel. Weld. Int. 2018, 32, 485–496. [Google Scholar] [CrossRef]
- Zhang, T.; Li, H.; Liu, S.; Shen, S.; Xie, H.; Shi, W.; Zhang, G.; Shen, B.; Chen, L.; Xiao, B.; et al. Evolution of molten pool during selective laser melting of Ti-6Al-4V. J. Phys. D Appl. Phys. 2019, 52, 055302. [Google Scholar] [CrossRef]



























| D10 | D50 | D90 |
|---|---|---|
| 19 | 29 | 41 |
| Ni | Cr | Fe | Al | Co | Cu | Mn | Mo | Nb | Si | Ta | Ti | B | C |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 52.5 | 19.5 | 17.3 | 0.5 | 0.5 | 0.15 | 0.175 | 3.05 | 5.125 | 0.175 | 0.025 | 0.9 | 0.003 | 0.04 |
| GENERAL SPECIFICATION | ENAVISION 250 |
|---|---|
| Production Volume (mm3) | 250 × 250 × 300 (9.8 × 9.8 × 11.8 inch) |
| Adjustable Layer Height | 20–100 μm (0.0007–0.004 inch) |
| Laser Type | Fiber Laser |
| Laser Power | 500W |
| Scanning Speed | Up to 11 m/s (433.07 inch) |
| Scanning System | 3D Dynamic Focused Scanning System |
| Dimension | (L × W × H) 2700 × 1440 × 2030 (106.3 × 56.7 × 79.9 inch) |
| Voltage | 400 V, 3 PH, 50/60 Hz |
| Current | 32 A |
| Inert Gas | Argon/Nitrogen |
| 02 Level | 100 ppm |
| Vacuum Pomp | Yes |
| Operating System | Operating SystemWindows 10/X |
| CONTROL UNIT | |
| Control System | Beckhoff Industrial PC |
| Processor | ProcessorIntel i5–i7 |
| Operating System | Windows 10/X |
| HMI | 15.6 inch, Touch Operated |
| SOFTWARE | |
| Data Preparation Software | Materilliase Magics and Modules |
| Data Processing Software | Ermaksan Build Processor |
| Supported File Types | STL, 3MF, AMF, DAE, FBX, VRML. |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ur Rehman, A.; Pitir, F.; Salamci, M.U. Laser Powder Bed Fusion (LPBF) of In718 and the Impact of Pre-Heating at 500 and 1000 °C: Operando Study. Materials 2021, 14, 6683. https://doi.org/10.3390/ma14216683
Ur Rehman A, Pitir F, Salamci MU. Laser Powder Bed Fusion (LPBF) of In718 and the Impact of Pre-Heating at 500 and 1000 °C: Operando Study. Materials. 2021; 14(21):6683. https://doi.org/10.3390/ma14216683
Chicago/Turabian StyleUr Rehman, Asif, Fatih Pitir, and Metin Uymaz Salamci. 2021. "Laser Powder Bed Fusion (LPBF) of In718 and the Impact of Pre-Heating at 500 and 1000 °C: Operando Study" Materials 14, no. 21: 6683. https://doi.org/10.3390/ma14216683
APA StyleUr Rehman, A., Pitir, F., & Salamci, M. U. (2021). Laser Powder Bed Fusion (LPBF) of In718 and the Impact of Pre-Heating at 500 and 1000 °C: Operando Study. Materials, 14(21), 6683. https://doi.org/10.3390/ma14216683