Fragmentation of Beaded Fibres in a Composite
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Beaded Fibre Preparation
2.3. Single Fibre Fragmentation Tests
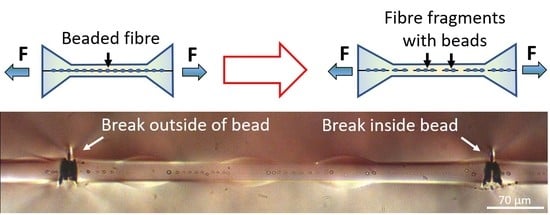
2.3.1. Background
2.3.2. Specimen Fabrication
2.3.3. Test Procedure
3. Results
3.1. Qualitative Analysis under Cross-Polarised Light
3.2. Fragmentation Behaviour and Effective Interfacial Strength
3.3. Distribution of Breaks and Critical Number of Beads
4. Discussion
4.1. Mechanical Interlocking
4.2. Effect of Beads Size and Fibre Volume Fraction
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Determination of Average Fibre Strength at ()
Background
Method 1: Obtaining Weibull Parameters from Fibres at a Single Gauge Length
Method 2: Obtaining Weibull Parameters from Filaments at Three Different Gauge Lengths
Single Fibre Tensile Tests and Results


| Method 1 | Method 2 | ||
|---|---|---|---|
| Scale parameter (m) | 4.69 | 5.10 | |
| Shape parameter () (MPa) | 1466 | 3007 | |
| Control (MPa) | = 0.52 mm | 3179 ± 86 | 3131 ± 79 |
| Beaded fibre (MPa) | = 0.45 mm | 3272 ± 74 | 3217 ± 68 |
Appendix B
Compressive Residual Strain in Fibre due to Beads
Appendix C
References
- Sager, R.J.; Klein, P.J.; Lagoudas, D.C.; Zhang, Q.; Liu, J.; Dai, L.; Baur, J.W. Effect of carbon nanotubes on the interfacial shear strength of T650 carbon fiber in an epoxy matrix. Compos. Sci. Technol. 2009, 69, 898–904. [Google Scholar] [CrossRef]
- Graupner, N.; Rößler, J.; Ziegmann, G.; Müssig, J. Fibre/matrix adhesion of cellulose fibres in PLA, PP and MAPP: A critical review of pull-out test, microbond test and single fibre fragmentation test results. Compos. Part A Appl. Sci. Manuf. 2014, 63, 133–148. [Google Scholar] [CrossRef]
- Herrera-Franco, P.J.; Drzal, L.T. Comparison of methods for the measurement of fibre/matrix adhesion in composites. Composites 1992, 23, 2–27. [Google Scholar] [CrossRef]
- Ehrburger, P.; Donnet, J.B. Interface in composite materials. Philos. Trans. R. Soc. London Ser. A Math. Phys. Sci. 1980, 294, 495–505. [Google Scholar] [CrossRef]
- Tanoglu, M.; McKnight, S.H.; Palmese, G.R.; Gillespie, J.W. Effects of glass-fiber sizings on the strength and energy absorption of the fiber/matrix interphase under high loading rates. Compos. Sci. Technol. 2001, 61, 205–220. [Google Scholar] [CrossRef] [Green Version]
- Gnädinger, F.; Middendorf, P.; Fox, B. Interfacial shear strength studies of experimental carbon fibres, novel thermosetting polyurethane and epoxy matrices and bespoke sizing agents. Compos. Sci. Technol. 2016, 133, 104–110. [Google Scholar] [CrossRef]
- Ritchie, R.O. The conflicts between strength and toughness. Nat. Mater. 2011, 10, 817–822. [Google Scholar] [CrossRef]
- Rodricks, C.W.; Greenfeld, I.; Wagner, H.D. Polymer beads as interfacial obstacles in fibre composites. Compos. Sci. Technol. 2021, 210, 108793. [Google Scholar] [CrossRef]
- Greenfeld, I.; Rodricks, C.W.; Sui, X.; Wagner, H.D. Beaded fiber composites—Stiffness and strength modeling. J. Mech. Phys. Solids 2019, 125, 384–400. [Google Scholar] [CrossRef]
- Greenfeld, I.; Zhang, W.; Sui, X.M.; Wagner, H.D. Intermittent beading in fiber composites. Compos. Sci. Technol. 2018, 160, 21–31. [Google Scholar] [CrossRef]
- Shi, S.; Yang, C.; Nie, M. Enhanced interfacial strength of natural fiber/polypropylene composite with mechanical-interlocking interface. ACS Sustain. Chem. Eng. 2017, 5, 10413–10420. [Google Scholar] [CrossRef]
- Wegst, U.G.K.; Bai, H.; Saiz, E.; Tomsia, A.P.; Ritchie, R.O. Bioinspired structural materials. Nat. Mater. 2015, 14, 23–36. [Google Scholar] [CrossRef] [PubMed]
- Torres, A.M.; Trikanad, A.A.; Aubin, C.A.; Lambers, F.M.; Luna, M.; Rimnac, C.M.; Zavattieri, P.; Hernandez, C.J. Bone-inspired microarchitectures achieve enhanced fatigue life. Proc. Natl. Acad. Sci. USA 2019, 116, 24457–24462. [Google Scholar] [CrossRef] [PubMed]
- Humburg, H.; Zhu, D.; Beznia, S.; Barthelat, F. Bio-inspired tapered fibers for composites with superior toughness. Compos. Sci. Technol. 2012, 72, 1012–1019. [Google Scholar] [CrossRef]
- Blaker, J.J.; Anthony, D.B.; Tang, G.; Shamsuddin, S.R.; Kalinka, G.; Weinrich, M.; Abdolvand, A.; Shaffer, M.S.P.; Bismarck, A. Property and shape modulation of carbon fibers using lasers. ACS Appl. Mater. Interfaces 2016, 8, 16351–16358. [Google Scholar] [CrossRef] [Green Version]
- Zhu, Y.T.; Beyerlein, I.J. Bone-shaped short fiber composites—An overview. Mater. Sci. Eng. A 2002, 326, 208–227. [Google Scholar] [CrossRef]
- Fu, S.; Zhou, B.; Lung, C. On the pull-out of fibres with a branched structure and the inference of strength and fracture toughness of composites. Compos. Sci. Technol. 1993, 47, 245–250. [Google Scholar] [CrossRef]
- Barthelat, F.; Yin, Z.; Buehler, M.J. Structure and mechanics of interfaces in biological materials. Nat. Rev. Mater. 2016, 1, 16007. [Google Scholar] [CrossRef]
- Barthelat, F.; Espinosa, H.D. An experimental investigation of deformation and fracture of nacre—Mother of pearl. Exp. Mech. 2007, 47, 311–324. [Google Scholar] [CrossRef]
- Naleway, S.E.; Porter, M.M.; McKittrick, J.; Meyers, M.A. Structural design elements in biological materials: Application to bioinspiration. Adv. Mater. 2015, 27, 5455–5476. [Google Scholar] [CrossRef] [Green Version]
- Weiner, S.; Traub, W.; Wagner, H.D. Lamellar bone: Structure–function relations. J. Struct. Biol. 1999, 126, 241–255. [Google Scholar] [CrossRef] [PubMed]
- Laurent, C.M.; Palmer, C.; Boardman, R.P.; Dyke, G.; Cook, R.B. Nanomechanical properties of bird feather rachises: Exploring naturally occurring fibre reinforced laminar composites. J. R. Soc. Interface 2014, 11, 20140961. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lingham-Soliar, T.; Bonser, R.H.C.; Wesley-Smith, J. Selective biodegradation of keratin matrix in feather rachis reveals classic bioengineering. Proc. R. Soc. B Biol. Sci. 2010, 277, 1161–1168. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Feih, S.; Wonsyld, K.; Minzari, D.; Westermann, P.; Lilholt, H. Testing Procedure for the Single Fiber Fragmentation Test; Technical Report no. Risø-R-1483(EN); Risø National Laboratory: Roskilde, Denmark, 2004. [Google Scholar]
- Tripathi, D.; Jones, F.R. Single fibre fragmentation test for assessing adhesion in fibre reinforced composites. J. Mater. Sci. 1998, 33, 1–16. [Google Scholar] [CrossRef]
- Awal, A.; Cescutti, G.; Ghosh, S.; Müssig, J. Interfacial studies of natural fibre/polypropylene composites using single fibre fragmentation test (SFFT). Compos. Part A Appl. Sci. Manuf. 2011, 42, 50–56. [Google Scholar] [CrossRef]
- Detassis, M.; Pegoretti, A.; Migliaresi, C.; Wagner, H.D. Experimental evaluation of residual stresses in single fibre composites by means of the fragmentation test. J. Mater. Sci. 1996, 31, 2385–2392. [Google Scholar] [CrossRef]
- Feillard, P.; Désarmot, G.; Favre, J.P. A critical assessment of the fragmentation test for glass/epoxy systems. Compos. Sci. Technol. 1993, 49, 109–119. [Google Scholar] [CrossRef]
- Lacroix, T.; Keunings, R.; Desaeger, M.; Verpoest, I. A new data reduction scheme for the fragmentation testing of polymer composites. J. Mater. Sci. 1995, 30, 683–692. [Google Scholar] [CrossRef]
- Kelly, A.; Tyson, W.R. Tensile properties of fibre-reinforced metals: Copper/tungsten and copper/molybdenum. J. Mech. Phys. Solids 1965, 13, 329–350. [Google Scholar] [CrossRef]
- Cottrell, A.H. Strong solids. Proc. R. Soc. A Math. Phys. Eng. Sci. 1964, 282, 2–9. [Google Scholar] [CrossRef]
- Wagner, H.D.; Zhou, X.F. A twin-fiber fragmentation experiment. Compos. Part A Appl. Sci. Manuf. 1998, 29, 331–335. [Google Scholar] [CrossRef]
- Andersons, J.; Joffe, R.; Hojo, M.; Ochiai, S. Fibre fragment distribution in a single-fibre composite tension test. Compos. Part B Eng. 2001, 32, 323–332. [Google Scholar] [CrossRef]
- Davies, G.D. Durability of adhesive joints. In Handbook of Adhesive Technology, Revised and Expanded; Pizzi, A., Mittal, K.L., Eds.; CRC Press: Boca Raton, FL, USA, 2003; pp. 273–291. ISBN 9780203912225. [Google Scholar]
- Maxwell, A.S.; Broughton, W.; Lodeiro, M.; Shaw, R. NPL Report MN 7 Measurement of Residual Stresses and Strains in Carbon Fibre Composites. Available online: https://eprintspublications.npl.co.uk/4441/1/MN7.pdf (accessed on 15 June 2021).
- Da Silva, L.F.M. Improving bonding at high and low temperatures. In Woodhead Publishing in Materials, Advances in Structural Adhesive Bonding; Dillard, D.A., Ed.; Woodhead Publishing: Cambridge, UK, 2010; pp. 516–546. ISBN 9781845694357. [Google Scholar]
- Greenfeld, I.; Wagner, H.D. Nanocomposite toughness, strength and stiffness: Role of filler geometry. Nanocomposites 2015, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Lamanna, G.; Ceparano, A. Mechanical characterization of sheet moulding composites for the automotive industry. Open Mater. Sci. J. 2014, 8, 108–113. [Google Scholar] [CrossRef] [Green Version]
- Prime, B.R.; Gotro, J. Thermoset Characterization. Available online: https://polymerinnovationblog.com/ebook-store/thermoset-characterization/ (accessed on 6 October 2021).










| Control | Beaded Fibre | p-Value (t-Test) | |
|---|---|---|---|
| Average # breaks at saturation | 28.5 ± 3.6 | 32.8 ± 3.5 | 0.0002 |
| Median # breaks | 28.5 | 32 | |
| (mm) | 0.40 | 0.35 | |
| (mm) | 0.54 | 0.47 | |
| (MPa) * | 3179 ± 85 | 3272 ± 74 | |
| (MPa) | 50.7 ± 7.7 | 59.6 ± 7.8 | 0.0002 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rodricks, C.W.; Greenfeld, I.; Fiedler, B.; Wagner, H.D. Fragmentation of Beaded Fibres in a Composite. Materials 2022, 15, 890. https://doi.org/10.3390/ma15030890
Rodricks CW, Greenfeld I, Fiedler B, Wagner HD. Fragmentation of Beaded Fibres in a Composite. Materials. 2022; 15(3):890. https://doi.org/10.3390/ma15030890
Chicago/Turabian StyleRodricks, Carol Winnifred, Israel Greenfeld, Bodo Fiedler, and Hanoch Daniel Wagner. 2022. "Fragmentation of Beaded Fibres in a Composite" Materials 15, no. 3: 890. https://doi.org/10.3390/ma15030890
APA StyleRodricks, C. W., Greenfeld, I., Fiedler, B., & Wagner, H. D. (2022). Fragmentation of Beaded Fibres in a Composite. Materials, 15(3), 890. https://doi.org/10.3390/ma15030890