Tensile Deformation Behaviors of Pure Ti with Different Grain Sizes under Wide-Range of Strain Rate
Abstract
:1. Introduction
2. Materials and Methods
3. Results
3.1. Initial Microstructure
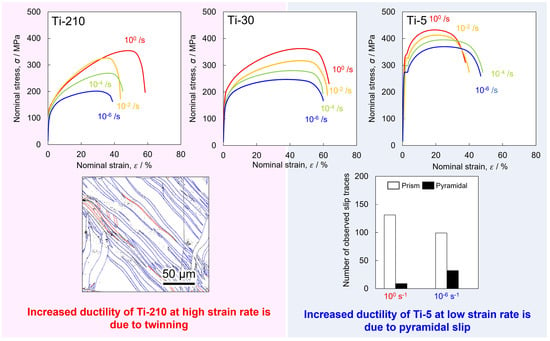
3.2. Evaluation of Mechanical Properties by Tensile Testing
3.3. Evaluation of Mechanical Properties by Tensile Testing
4. Discussion
4.1. Effect of Strain Rates on Twinning
4.2. Effect of Grain Size on Twinning and Work-Hardening Behavior
5. Conclusions
- In all the samples, the 0.2% proof stress and ultimate tensile strength increased with an increase in the strain rate. At the same strain rates, the samples with finer grain sizes exhibited higher strengths. The variation in fracture strain was different for each sample: for Ti-210, the fracture strain increased with increasing strain rates. In contrast, for Ti-5, the fracture strain decreased with increasing strain rates. For Ti-30, the variation in the fracture strain with strain rate was negligible.
- In Ti-30 and Ti-210, the frequency of twinning increased with an increase in the strain. At low strains, twins were preferentially formed, and as deformation progressed, twins formed more frequently. At high strain rates (100 s−1), the frequency of twinning was higher than that at low strain rates (10−6 s−1), and thin twins tended to form more frequently. For Ti-5, the frequency of twinning did not change with an increase in the strain.
- When Ti-30 was deformed at high (100 s−1) and low (10−6 s−1) strain rates up to approximately 15%, the frequency of pyramidal slips tended to increase at low strain rates (10−6 s−1). This change in the frequency of the pyramidal slip activity affects the frequency of twinning.
- In Ti-5, pyramidal slip was more activated at low strain rates than at high strain rates.
- For Ti-210 and Ti-30, the work-hardening rate varied as an S-shaped curve. This corresponded to the introduction of twinning.
- In Ti-210, the greater fracture strain and work-hardening ability at higher strain rates were because of the higher frequency of twinning. In Ti-5, wherein the frequency of twinning was lower, the higher fracture strain at lower strain rates was attributed to the activity of the 1st order pyramidal slip. In Ti-30, the fracture strain was constant regardless of the strain rate. This is because of the contribution of twinning at high strain rates and pyramidal slip at low strain rates.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Orozco-Caballero, A.; Li, F.; Ojos, D.E.-D.L.; Atkinson, M.D.; da Fonseca, J.Q. On the ductility of alpha titanium: The effect of temperature and deformation mode. Acta Mater. 2018, 149, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Salem, A.A.; Kalidindi, S.R.; Doherty, R.D. Strain hardening of titanium: Role of deformation twinning. Acta Mater. 2003, 51, 4225–4237. [Google Scholar] [CrossRef]
- Chun, Y.B.; Yu, S.H.; Semiatin, S.L.; Hwang, S.K. Effect of deformation twinning on microstructure and texture evolution during cold rolling of CP-titanium. Mater. Sci. Eng. A 2005, 398, 209–219. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Guo, W.G.; Cheng, J.Y. Mechanical properties and deformation mechanisms of a commercially pure titanium. Acta Mater. 1999, 47, 3705–3720. [Google Scholar] [CrossRef] [Green Version]
- D’yakonov, G.S.; Zherebtsov, S.V.; Klimova, M.V.; Salishchev, G.A. Microstructure evolution of commercial purity titanium during cryorolling. Phys. Met. Metallogr. 2015, 116, 182–188. [Google Scholar] [CrossRef]
- Wang, T.; Li, B.; Li, M.; Li, Y.; Wang, Z.; Nie, Z. Effects of strain rates on deformation twinning behavior in α-titanium. Mater. Charact. 2015, 106, 218–225. [Google Scholar] [CrossRef]
- Lee, M.-S.; Jo, A.-R.; Hwang, S.-K.; Hyun, Y.-T.; Jun, T.-S. The role of strain rate and texture in the deformation of commercially pure titanium at cryogenic temperature. Mater. Sci. Eng. A 2021, 827, 142042. [Google Scholar] [CrossRef]
- Tsukamoto, G.; Kunieda, T.; Yamasaki, S.; Mitsuhara, M.; Nakashima, H. Effects of temperature and grain size on active twinning systems in commercially pure titanium. J. Alloys Compd. 2021, 884, 161154. [Google Scholar] [CrossRef]
- Paton, N.E.; Backofen, W.A. Plastic deformation of titanium at elevated temperatures. Metall. Trans. 1970, 1, 2839–2847. [Google Scholar] [CrossRef]
- Deng, X.G.; Hui, S.X.; Ye, W.J.; Song, X.Y. Analysis of twinning behavior of pure Ti compressed at different strain rates by Schmid factor. Mater. Sci. Eng. A 2013, 575, 15–20. [Google Scholar] [CrossRef]
- Gurao, N.P.; Kapoor, R.; Suwas, S. Deformation behaviour of commercially pure titanium at extreme strain rates. Acta Mater. 2011, 59, 3431–3446. [Google Scholar] [CrossRef]
- Won, J.W.; Choi, S.-W.; Yeom, J.-T.; Hyun, Y.-T.; Lee, C.S.; Park, S.H. Anisotropic twinning and slip behaviors and their relative activities in rolled alpha-phase titanium. Mater. Sci. Eng. A 2017, 698, 54–62. [Google Scholar] [CrossRef]
- Wang, B.; Liu, H.; Zhang, Y.; Zhou, B.; Deng, L.; Wang, C.; Chen, J.; Zhang, Y. Effect of grain size on twinning behavior of pure titanium at room temperature. Mater. Sci. Eng. A 2021, 827, 142060. [Google Scholar] [CrossRef]
- Murayama, Y.; Obara, K.; Ikeda, K. Effects of deformation twinning on the deformation behavior of textured titanium sheets in plane strain compressive tests. Mater. Trans. 1991, 32, 854–861. [Google Scholar] [CrossRef] [Green Version]
- Murayama, Y.; Obara, K.; Ikeda, K. Effect of twinning on deformation of textured commercially-pure Ti sheets under plane stress states. Mater. Trans. JIM 1993, 34, 801–808. [Google Scholar] [CrossRef] [Green Version]
- Chichili, D.R.; Ramesh, K.T.; Hemker, K.J. The high-strain-rate response of alpha-titanium: Experiments, deformation mechanisms and modeling. Acta Mater. 1998, 46, 1025–1043. [Google Scholar] [CrossRef]
- Ahn, K.; Huh, H.; Yoon, J. Rate-dependent hardening model for pure titanium considering the effect of deformation twinning. Int. J. Mech. Sci. 2015, 98, 80–92. [Google Scholar] [CrossRef]
- Luan, Q.; Britton, T.B.; Jun, T.-S. Strain rate sensitivity in commercial pure titanium: The competition between slip and deformation twinning. Mater. Sci. Eng. A 2018, 734, 385–397. [Google Scholar] [CrossRef]
- Yamamoto, S.; Miyajima, Y.; Watanabe, C.; Monzen, R.; Tsuru, T.; Miura, H. Dependences of grain size and strain-rate on deformation behavior of commercial purity titanium processed by multi-directional forging. Mater. Trans. 2020, 61, 2320–2328. [Google Scholar] [CrossRef]
- Warwick, J.L.W.; Jones, N.G.; Rahman, K.M.; Dye, D. Lattice strain evolution during tensile and compressive loading of CP Ti. Acta Mater. 2012, 60, 6720–6731. [Google Scholar] [CrossRef]
- Becker, H.; Pantleon, W. Work-hardening stages and deformation mechanism maps during tensile deformation of commercially pure titanium. Comput. Mater. Sci. 2013, 76, 52–59. [Google Scholar] [CrossRef]
- Deguchi, M.; Yamasaki, S.; Mitsuhara, M.; Nakashima, H.; Ota, Y. Dislocation motion and microstructure evolution deformed during creep at room temperature in Ti-6Al-4V alloy. J. Jpn. Inst. Light Met. 2020, 70, 405–414. [Google Scholar] [CrossRef]
- Zhu, C.; Chen, Y.; Xu, J.; Yu, H.; Shan, D.; Guo, B. Grain size and specimen thickness effects on twinning behaviors in high strain rate deformation of ultra-thin pure titanium sheet. Mater. Sci. Eng. A 2022, 832, 142417. [Google Scholar] [CrossRef]
- Won, J.W.; Park, C.H.; Hong, S.-G.; Lee, C.S. Deformation anisotropy and associated mechanisms in rolling textured high purity titanium. J. Alloys Compd. 2015, 651, 245–254. [Google Scholar] [CrossRef]
- Kishida, K.; Kim, J.G.; Nagae, T.; Inui, H. Experimental evaluation of critical resolved shear stress for the first-order pyramidal c + a slip in commercially pure Ti by micropillar compression method. Acta Mater. 2020, 196, 168–174. [Google Scholar] [CrossRef]
- Baudoin, P.; Hama, T.; Takuda, H. Influence of critical resolved shear stress ratios on the response of a commercially pure titanium oligocrystal: Crystal plasticity simulations and experiment. Int. J. Plast. 2019, 115, 111–131. [Google Scholar] [CrossRef]
- Rodríguez-Galán, D.; Sabirov, I.; Segurado, J. Temperature and strain rate effect on the deformation of nanostructured pure titanium. Int. J. Plast. 2015, 70, 191–205. [Google Scholar] [CrossRef]
- Li, W.; Yamasaki, S.; Mitsuhara, M.; Nakashima, H. In situ EBSD study of deformation behavior of primary α phase in a bimodal Ti-6Al-4V alloy during uniaxial tensile tests. Mater. Charact. 2020, 163, 110282. [Google Scholar] [CrossRef]
- Jones, I.P.; Hutchinson, W.B. Stress-state dependence of slip in titanium-6Al-4V and other H.C.P metals. Acta Metall. 1981, 29, 951–968. [Google Scholar] [CrossRef]
- Ghaderi, A.; Barnett, M.R. Sensitivity of deformation twinning to grain size in titanium and magnesium. Acta Mater. 2011, 59, 7824–7839. [Google Scholar] [CrossRef]
- Lederich, R.J.; Sastry, S.M.L.; O’Neal, J.E.; Rath, B.B. The effect of grain size on yield stress and work hardening of polycrystalline titanium at 295 K and 575 K. Mater. Sci. Eng. 1978, 33, 183–188. [Google Scholar] [CrossRef]
- Tsukamoto, G.; Kunieda, T.; Mitsuhara, M.; Nakashima, H. Effect of twinning deformation on work hardening in commercially pure titanium. Mater. Sci. Eng. A 2022, 840, 142907. [Google Scholar] [CrossRef]
- Salem, A.A.; Kalidindi, S.R.; Doherty, R.D. Strain hardening regimes and microstructure evolution during large strain compression of high purity titanium. Scr. Mater. 2002, 46, 419–423. [Google Scholar] [CrossRef]
- Wu, X.; Yang, M.; Yuan, F.; Wu, G.; Wei, Y.; Huang, X.; Zhu, Y. Heterogeneous lamella structure unites ultrafine-grain strength with coarse-grain ductility. Proc. Natl. Acad. Sci. USA 2015, 112, 14501–14505. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, Z.; Fu, L.; Fu, B.; Shan, A. Yield point elongation in fine-grained titanium. Mater. Lett. 2013, 96, 1–4. [Google Scholar] [CrossRef]
- Xu, T.; Wang, S.; Wang, W.; Liang, P.; Li, X.; Mitsuzaki, N.; Chen, Z. Multimodal grain structure and tensile properties of cold-rolled titanium after short-duration annealing. Mater. Charact. 2020, 160, 110095. [Google Scholar] [CrossRef]
- Remy, L. Kinetics of f.c.c. deformation twinning and its relationship to stress-strain behaviour. Acta Metall. 1978, 26, 443–451. [Google Scholar] [CrossRef]
















| Ti | Fe | O | N | C | H |
|---|---|---|---|---|---|
| Bal. | 0.03 | 0.03 | 0.002 | 0.006 | 0.0006 |
| Bal. | 0.03 | 0.05 | 0.01 | 0.01 | 0.002 |
| Specimen | [s−1] | ||||
|---|---|---|---|---|---|
| Ti-210 | 10−6 | Test-1 | 93 | 201 | 39 |
| Test-2 | 100 | 221 | 47 | ||
| 10−4 | Test-1 | 108 | 269 | 45 | |
| Test-2 | 106 | 270 | 46 | ||
| 10−2 | Test-1 | 120 | 326 | 55 | |
| Test-2 | 118 | 319 | 56 | ||
| 100 | Test-1 | 126 | 354 | 58 | |
| Test-2 | 134 | 350 | 59 | ||
| Ti-30 | 10−6 | Test-1 | 118 | 247 | 60 |
| Test-2 | 120 | 246 | 52 | ||
| 10−4 | Test-1 | 127 | 280 | 60 | |
| Test-2 | 147 | 301 | 57 | ||
| 10−2 | Test-1 | 148 | 317 | 63 | |
| Test-2 | 152 | 330 | 63 | ||
| 100 | Test-1 | 177 | 363 | 63 | |
| Test-2 | 167 | 361 | 65 | ||
| Ti-5 | 10−6 | Test-1 | 197 | 369 | 47 |
| Test-2 | 218 | 379 | 42 | ||
| 10−4 | Test-1 | 254 | 395 | 48 | |
| Test-2 | 250 | 402 | 48 | ||
| 10−2 | Test-1 | 316 | 413 | 40 | |
| Test-2 | 290 | 415 | 39 | ||
| 100 | Test-1 | 325 | 433 | 41 | |
| Test-2 | 315 | 434 | 39 |
| Specimen | ||
|---|---|---|
| Ti-210 | 0.019 | 0.035 |
| Ti-30 | 0.033 | 0.031 |
| Ti-5 | 0.036 | 0.011 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Deguchi, M.; Yamasaki, S.; Mitsuhara, M.; Nakashima, H.; Tsukamoto, G.; Kunieda, T. Tensile Deformation Behaviors of Pure Ti with Different Grain Sizes under Wide-Range of Strain Rate. Materials 2023, 16, 529. https://doi.org/10.3390/ma16020529
Deguchi M, Yamasaki S, Mitsuhara M, Nakashima H, Tsukamoto G, Kunieda T. Tensile Deformation Behaviors of Pure Ti with Different Grain Sizes under Wide-Range of Strain Rate. Materials. 2023; 16(2):529. https://doi.org/10.3390/ma16020529
Chicago/Turabian StyleDeguchi, Misaki, Shigeto Yamasaki, Masatoshi Mitsuhara, Hideharu Nakashima, Genki Tsukamoto, and Tomonori Kunieda. 2023. "Tensile Deformation Behaviors of Pure Ti with Different Grain Sizes under Wide-Range of Strain Rate" Materials 16, no. 2: 529. https://doi.org/10.3390/ma16020529
APA StyleDeguchi, M., Yamasaki, S., Mitsuhara, M., Nakashima, H., Tsukamoto, G., & Kunieda, T. (2023). Tensile Deformation Behaviors of Pure Ti with Different Grain Sizes under Wide-Range of Strain Rate. Materials, 16(2), 529. https://doi.org/10.3390/ma16020529