An Experimental Study of Mortars with Recycled Ceramic Aggregates: Deduction and Prediction of the Stress-Strain
Abstract
:1. Introduction
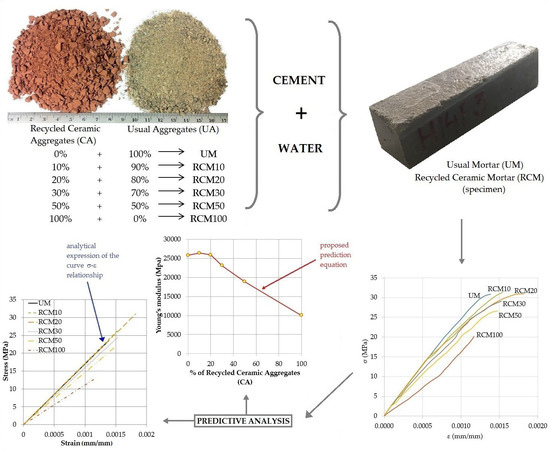
2. Materials and Methods
2.1. Materials and Mortar Dosage
2.2. Experimental Campaign/Specimens
2.3. Details of Tests and Procedures
3. Results
3.1. Density in Hardened State
3.2. Compression Strength
3.3. Calculation of E
3.4. Determining the Prediction Equations of the RCM
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| σ-ε | Stress-strain |
| CA | Recycled aggregates of ceramic |
| UA | Usual aggregates |
| RCM | Recycled ceramic mortars |
| CePo | Ceramic powder |
| c/a | Cement/aggregate |
| w/c | Water/cement |
| fm | Compressive strength |
| PS | Particle size |
| E | Module of elasticity or Young |
| εelastic | Elastic deformation |
| 0.40 fm | 40% of the maximum load of failure |
| εmax. | Maximum deformation of failure |
| Ur | Resiliency |
| T | Toughness |
| MOD | Bulk density in oven-dry condition |
| MSSD | Bulk density in saturated-surface-dry condition |
| DOD | Density in oven-dry condition |
| DSSD | Density in saturated-surface-dry condition |
| UM | Usual mortar |
| SEM | scanning electron microscope |
| G | Grout |
| ITZ | Interfacial transition zone |
| XRD | X-ray diffraction |
| RF | Replacement factor |
| PEr | Refined prediction equations |
| CC | Correctors coefficients |
| TC | Theoretical constants |
| OE | Objective equation |
| ED | Error Differential |
| S | Standard deviation |
| σelastic | Stress in the elastic range |
| σmax. | Up to maximum stress of failure |
References
- Higashiyama, H.; Yamauchi, K.; Sappakittipakorn, M.; Sano, M.; Takahashi, O. A visual investigation on chloride ingress into ceramic waste aggregate mortars having different water to cement ratios. Constr. Build. Mater. 2013, 40, 1021–1028. [Google Scholar] [CrossRef]
- Lavat, A.E.; Trezza, M.A.; Poggi, M. Characterization of ceramic roof tile wastes as pozzolanic admixture. Waste Manag. 2009, 29, 1666–1674. [Google Scholar] [CrossRef] [PubMed]
- Lázaro, C.; Trilles, V.R.; Gómez, F. Incorporación de residuos derivados de la fabricación cerámica y del vidrio reciclado en el proceso cerámico integral. Bol. Soc. Española Cerám. Vidr. 2012, 51, 139–144. [Google Scholar] [CrossRef]
- Corinaldesi, V. Environmentally-friendly bedding mortars for repair of historical buildings. Constr. Build. Mater. 2012, 35, 778–784. [Google Scholar] [CrossRef]
- Wild, S.; Khatib, J.M.; O′Farrell, M. Sulphate resistance of mortar, containing ground brick clay calcined at different temperatures. Cem. Concr. Res. 1997, 27, 697–709. [Google Scholar] [CrossRef]
- O′Farrell, M.; Wild, S.; Sabir, B.B. Resistance to chemical attack of ground brick-PC mortar Part I. Sodium sulphate solution. Cem. Concr. Res. 1999, 29, 1781–1790. [Google Scholar] [CrossRef]
- O’Farrell, M.; Wild, S.; Sabir, B.B. Resistance to chemical attack of ground brick ± PC mortar Part II. Synthetic seawater. Cem. Concr. Res. 2000, 30, 757–765. [Google Scholar] [CrossRef]
- O’Farrell, M.; Wild, S.; Sabir, B.B. Pore size distribution and compressive strength of waste clay brick mortar. Cem. Concr. Compos. 2001, 23, 81–91. [Google Scholar] [CrossRef]
- Moriconi, G.; Corinaldesi, V.; Antonucci, R. Environmentally-friendly mortars: A way to improve bond between mortar and brick. Mater. Struct. 2003, 36, 702–708. [Google Scholar] [CrossRef]
- Turanli, L.; Bektas, F.; Monteiro, P.J.M. Use of ground clay brick as a pozzolanic material to reduce the alkali–silica reaction. Cem. Concr. Res. 2003, 33, 1539–1542. [Google Scholar] [CrossRef]
- O′Farrell, M.; Sabir, B.B.; Wild, S. Strength and chemical resistance of mortars containing brick manufacturing clays subjected to different treatments. Cem. Concr. Compos. 2006, 28, 790–799. [Google Scholar] [CrossRef]
- Toledo Filho, R.D.; Gonçalves, J.P.; Americano, B.B.; Fairbairn, E.M.R. Potential for use of crushed waste calcined-clay brick as a supplementary cementitious material in Brazil. Cem. Concr. Res. 2007, 37, 1357–1365. [Google Scholar] [CrossRef]
- Puertas, F.; García-Díaz, I.; Palacios, M.; Martínez-Ramírez, S. Empleo de residuos cerámicos como materia prima alternativa para la fabricación de clínker de cemento portland. Cem. Hormigón 2007, 907, 20–34. [Google Scholar]
- Pereira-de-Oliveira, L.A.; Castro-Gomes, J.P.; Santos, P.M.S. The potential pozzolanic activity of glass and red-clay ceramic waste as cement mortars components. Constr. Build. Mater. 2012, 31, 197–203. [Google Scholar] [CrossRef]
- Wang, G.; Tian, B. Effect of Waste Ceramic Polishing Powder on the Properties of Cement Mortars. In Proceedings of the International Conference on Energy and Environment Technology ICEET’09, Guilin, China, 16–18 October 2009; IEEE Computer Society: Washington, DC, USA, 2009; pp. 101–104. [Google Scholar]
- Kumavat, H.R.; Sonawane, Y.N. Feasibility Study of Partial Replacement of Cement and Sand in Mortar by Brick Waste Material. Int. J. Innov. Technol. Explor. Eng. 2013, 2, 17–20. [Google Scholar]
- Bektas, F.; Wang, K.; Ceylan, H. Effects of crushed clay brick aggregate on mortar durability. Constr. Build. Mater. 2009, 23, 1909–1914. [Google Scholar] [CrossRef]
- Silva, J.; Brito, J.; Veiga, R. Recycled Red-Clay Ceramic Construction and Demolition Waste for Mortars Production. J. Mater. Civ. Eng. 2010, 22, 236–244. [Google Scholar] [CrossRef]
- Silva, J.; Brito, J.; Veiga, R. Incorporation of fine ceramics in mortars. Constr. Build. Mater. 2009, 23, 556–564. [Google Scholar] [CrossRef]
- Silva, J.; Brito, J.; Veiga, R. Fine ceramics replacing cement in mortars Partial replacement of cement with fine ceramics in rendering mortars. Mater. Struct. 2008, 41, 1333–1344. [Google Scholar] [CrossRef]
- Ay, N.; Ünal, M. The use of waste ceramic tile in cement production. Cem. Concr. Res. 2000, 30, 497–499. [Google Scholar] [CrossRef]
- Jiménez, J.R.; Ayuso, J.; López, M.; Fernández, J.M.; Brito, J. Use of fine recycled aggregates from ceramic waste in masonry mortar manufacturing. Constr. Build. Mater. 2013, 40, 679–690. [Google Scholar] [CrossRef]
- Corinaldesi, V. Mechanical behavior of masonry assemblages manufactured with recycled-aggregate mortars. Cem. Concr. Compos. 2009, 31, 505–510. [Google Scholar] [CrossRef]
- Higashiyama, H.; Yagishita, F.; Sano, M.; Takahashi, O. Compressive strength and resistance to chloride penetration of mortars using ceramic waste as fine aggregate. Constr. Build. Mater. 2012, 26, 96–101. [Google Scholar] [CrossRef]
- Gesoǧlu, M.; Güneyisi, E.; Özturan, T. Effects of end conditions on compressive strength and static elastic modulus of very high strength concrete. Cem. Concr. Res. 2002, 32, 1545–1550. [Google Scholar] [CrossRef]
- Demir, F.; Korkmaz, K.A. Prediction of lower and upper bounds of elastic modulus of high strength concrete. Constr. Build. Mater. 2008, 22, 1385–1393. [Google Scholar] [CrossRef]
- Suto, H. Relation between Modulus of Elasticity and Compressive Strength of Ultrahigh-Strength Mortar with Mixed Silicon Carbide as Fine Aggregate. J. Mater. Sci. Technol. 2001, 17, 579–580. [Google Scholar]
- Zhou, J.; Chen, X. Stress-Strain Behavior and Statistical Continuous Damage Model of Cement Mortar under High Strain Rates. J. Mater. Civ. Eng. 2013, 1, 120–130. [Google Scholar] [CrossRef]
- Martínez, P.; Azuaga, M. Medición del Módulo de Elasticidad de Young. Available online: http://www.fisicarecreativa.com/informes/infor_mecanica/young97.pdf (accessed on 10 January 2016).
- Candelario, M.P. Propiedades Mecánicas de los Materiales. METALOGRAFÍA—UNIVERSIDAD TECNOLÓGICA DE PEREIRA. Available online: http://blog.utp.edu.co/metalografia/2-propiedades-mecanicas-de-los-materiales/ (accessed on 4 April 2015).
- Lima, P.R.L.; Toledo, R.D.; Melo, J.A. Compressive Stress-strain Behaviour of Cement Mortar-composites Reinforced with Short Sisal Fibre. Mater. Res. 2014, 17, 38–46. [Google Scholar] [CrossRef]
- Serrano-Guzmán, M.F.; Perez-Ruiz, D.D. Análisis de sensibilidad para estimar el módulo de elasticidad estático del concreto. Concr. Cem. Investig. Desarro. 2010, 2, 17–30. [Google Scholar]
- Standard Specification for Aggregate for Masonry Mortar; ASTM C144-99; American Society for Testing and Materials: West Conshohocken, PA, USA, 1999.
- Standard Test Method for Density, Relative Density (Specific Gravity), and Absorption; ASTM C128-04a; American Society for Testing and Materials: West Conshohocken, PA, USA, 2004.
- Standard Test Method for Sieve Analysis of Fine and Coarse Aggregates; ASTM C136-06; American Society for Testing and Materials: West Conshohocken, PA, USA, 2006.
- Standard Test Method for Materials Finer than 75-µm (No. 200) Sieve in Mineral; ASTM C117-95; American Society for Testing and Materials: West Conshohocken, PA, USA, 1995.
- Parte 1: Composición, Especificaciones y Criterios de Conformidad de los Cementos Comunes; AENOR, UNE-EN 197-1; Asociación Española de Normalización y Certificación: Madrid, España, 2011.
- Sagoe-Crentsil, K.K.; Brown, T.; Taylor, A.H. Performance of concrete made with commercially produced coarse recycled concrete aggregate. Cem. Concr. Res. 2001, 31, 707–712. [Google Scholar] [CrossRef]
- García-González, J.; Rodríguez-Robles, D.; Juan-Valdés, A.; Morán del Pozo, J.M.; Guerra-Romero, M.I. Pre-saturation technique of the recycled aggregates: Solution to the water absorption drawback in the recycled concrete manufacture. Materials 2014, 7, 6224–6236. [Google Scholar] [CrossRef]
- Mechanical Mixing of Hydraulic Cement Pastes and Mortars of Plastic Consistency; ASTM C305-06; American Society for Testing and Materials: West Conshohocken, PA, USA, 2006.
- Standard Specification for Flow Table for Use in Tests of Hydraulic Cement; ASTM C230/C230M-03; American Society for Testing and Materials: West Conshohocken, PA, USA, 2003.
- Standard Test Method for Air Content of Freshly Mixed Concrete by the Pressure Method; ASTM C231-08b; American Society for Testing and Materials: West Conshohocken, PA, USA, 2008.
- Standard Test Method for Compressive Strength of Hydraulic Cement Mortars; ASTM C109/C109M-05; American Society for Testing and Materials: West Conshohocken, PA, USA, 2005.
- Parte 10: Determinación de la Densidad Aparente en Seco del Mortero Endurecido; AENOR, UNE-EN 1015-10; Asociación Española de Normalización y Certificación: Madrid, España, 2000.
- Determinación de la Densidad Real y Aparente y de la Porosidad Abierta y Total; AENOR, UNE-EN 1936; Asociación Española de Normalización y Certificación: Madrid, España, 2007.
- Standard Test Method for Compressive Strength of Hydraulic-Cement Mortars (Using Portions of Prisms Broken in Flexure); ASTM C349-97; American Society for Testing and Materials: West Conshohocken, PA, USA, 1997.
- Fanella, D.A.; Naaman, A.E. Stress-strain Properties of Fiber Reinforced Mortar in Compression. ACI J. 1985, 82, 475–483. [Google Scholar]
- Ávila, O.; Carrillo, J.; Alcocer, S.M. Rehabilitación de muros de concreto usando CRFA: Ensayos en mesa vibradora. Concreto Cem. Investig. Desarro. 2011, 2, 2–17. [Google Scholar]
- Corinaldesi, V.; Moriconi, G. Behaviour of cementitious mortars containing different kinds of recycled aggregate. Constr. Build. Mater. 2009, 23, 289–294. [Google Scholar] [CrossRef]
- Norme Française Homologué, “Mesure du Module D’élasticité Dynamique”; AFNOR, NF B10-511; Association française de Normalisation: Paris, Francia, 1975.
- FrontlineSolvers. Available online: http://www.solver.com (accessed on 1 July 2015).












| Property 1 | CA | UA |
|---|---|---|
| Without adjusted granulometric profiles | ||
| MOD (kg/m3) | 1182.0 | 1735.1 |
| MSSD (kg/m3) | 1399.1 | 1860.8 |
| Void content (%) | 35.3 | 32.9 |
| With adjusted granulometric profiles | ||
| DOD (kg/m3) | 1820.9 | 2581.6 |
| DSSD (kg/m3) | 2155.4 | 2623.6 |
| Water absorption coefficient (%) | 18.4 | 1.6 |
| Fineness modulus materials | 2.8 | 2.4 |
| Particles < 75 µm (sieve No. 200) (%) | 8.2 | 2.9 |
| Materials (g) | Classification and Proportions of the Mixtures | ||||||
|---|---|---|---|---|---|---|---|
| UM | RCM10 | RCM20 | RCM30 | RCM50 | RCM100 | ||
| Water | 334 | 390 | 355 | 373 | 397 | 476 | |
| Cement | 400 | 433 | 381 | 372 | 348 | 323 | |
| UA 1 | <sieve No. 30 | 800 | 780 | 610 | 521 | 348 | 0 |
| >sieve No. 30 | 800 | 780 | 610 | 521 | 348 | 0 | |
| CA 1 | <sieve No. 30 | 0 | 69 | 122 | 179 | 278 | 517 |
| >sieve No. 30 | 0 | 104 | 183 | 268 | 417 | 775 | |
| Study Variables | ρ (g/cm3) |
|---|---|
| UM | 1.950 |
| RCM10 | 1.948 |
| RCM20 | 1.894 |
| RCM30 | 1.864 |
| RCM50 | 1.798 |
| RCM100 | 1.529 |
| Study Variables | fm (MPa) | 0.40 fm (MPa) | E (MPa) | T (MPa) | Ur (MPa) | εelastic (mm/mm) | εmax. (mm/mm) | E0 (MPa) |
|---|---|---|---|---|---|---|---|---|
| UATM | 28.77 ± 2.28 | 11.51 ± 0.91 | 26252 ± 41 | 0.024 ± 1.8 × 10−4 | 0.003 ± 2.53 × 10−4 | 0.0004 ± 2.18 × 10−5 | 0.0014 ± 2.03 × 10−5 | 23619 ± 1004 |
| CRM10 | 30.58 ± 1.12 | 12.23 ± 0.45 | 26514 ± 53 | 0.029 ± 1.77 × 10−3 | 0.003 ± 7.29 × 10−5 | 0.0005 ± 6.46 × 10−6 | 0.0016 ± 6.53 × 10−5 | 21710 ± 520 |
| CRM20 | 30.95 ± 1.44 | 12.38 ± 0.58 | 26251 ± 31 | 0.035 ± 7 × 10−4 | 0.003 ± 1.4 × 10−4 | 0.0005 ± 2 × 10−5 | 0.0018 ± 3.1 × 10−5 | 20249 ± 542 |
| CRM30 | 30.10 ± 0.99 | 12.04 ± 0.40 | 24064 ± 6 | 0.025 ± 1.97 × 10−4 | 0.003 ± 8.92 × 10−5 | 0.0005 ± 1.45 × 10−5 | 0.0016 ± 3.46 × 10−5 | 21107 ± 304 |
| CRM50 | 26.76 ± 2.48 | 10.71 ± 0.99 | 21731 ± 25 | 0.022 ± 5 × 10−4 | 0.003 ± 1 × 10−4 | 0.0005 ± 2.98 × 10−5 | 0.0015 ± 2.06 × 10−6 | 18940 ± 745 |
| CRM100 | 20.56 ± 0.34 | 8.23 ± 0.14 | 14194 ± 30 | 0.010 ± 8 × 10−4 | 0.002 ± 1.5 × 10−4 | 0.0005 ± 3 × 10−5 | 0.0012 ± 2 × 10−5 | 15891 ± 643 |
| Study Variables | Corrector Coefficient (CC for Mechanical Properties of RCM) | |||
|---|---|---|---|---|
| E | εelastic | Ur | T | |
| UM | 0.9817 | 0.9380 | 1.0086 | 0.6651 |
| RCM10 | 0.9915 | 0.9553 | 1.0572 | 0.8075 |
| RCM20 | 0.9817 | 0.9734 | 1.0855 | 0.9880 |
| RCM30 | 0.8999 | 1.0380 | 1.0716 | 0.7127 |
| RCM50 | 0.8126 | 0.9910 | 1.0291 | 0.6129 |
| RCM100 | 0.5308 | 1.1043 | 0.7480 | 0.2968 |
| Study Variables | E (MPa) | εelastic (mm/mm) | Ur (MPa) | T (MPa) | ||||
|---|---|---|---|---|---|---|---|---|
| Expt. | Simul. | Expt. | Simul. | Expt. | Simul. | Expt. | Simul. | |
| UM | 26,252 | 25,771 | 0.0004 | 0.0004 | 0.003 | 0.002 | 0.024 | 0.018 |
| RCM10 | 26,515 | 26,334 | 0.0005 | 0.0004 | 0.003 | 0.002 | 0.029 | 0.025 |
| RCM20 | 26,251 | 25,493 | 0.0005 | 0.0004 | 0.003 | 0.002 | 0.035 | 0.035 |
| RCM30 | 24,065 | 22,578 | 0.0005 | 0.0005 | 0.003 | 0.003 | 0.025 | 0.020 |
| RCM50 | 21,731 | 18,127 | 0.0005 | 0.0005 | 0.003 | 0.002 | 0.022 | 0.015 |
| RCM100 | 14,194 | 8883 | 0.0005 | 0.0005 | 0.002 | 0.002 | 0.010 | 0.004 |
| PEr of the Curve σ-ε | Application | TC (for the σ-ε Curve of the RCM) | A | B | C | D |
|---|---|---|---|---|---|---|
| PEr for σelastic | 0 ≤ XX% ≤ 50 | 16,337 | 0.893 | 0.242 | −0.704 | 1.253 |
| PEr for σelastic | XX% = 100% | 16,337 | 1.245 | 0.253 | −0.704 | 1.242 |
| PEr for σmax. | 0 ≤ XX% ≤ 100 | 13,113 | 1.179 | 0.253 | −0.704 | 1.242 |
| XX% | Corrector Coefficient (CC for σ-ε Curve of the RCM) | |
|---|---|---|
| CC for PEr up to σelastic | CC for PEr up to σmax. | |
| 0 | 1.7739 | 1.0962 |
| 10 | 1.8005 | 1.1126 |
| 20 | 1.7788 | 1.0992 |
| 30 | 1.6677 | 1.0306 |
| 50 | 1.5276 | 0.9440 |
| 100 | 0.7174 | 0.7174 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cabrera-Covarrubias, F.G.; Gómez-Soberón, J.M.; Almaral-Sánchez, J.L.; Arredondo-Rea, S.P.; Gómez-Soberón, M.C.; Corral-Higuera, R. An Experimental Study of Mortars with Recycled Ceramic Aggregates: Deduction and Prediction of the Stress-Strain. Materials 2016, 9, 1029. https://doi.org/10.3390/ma9121029
Cabrera-Covarrubias FG, Gómez-Soberón JM, Almaral-Sánchez JL, Arredondo-Rea SP, Gómez-Soberón MC, Corral-Higuera R. An Experimental Study of Mortars with Recycled Ceramic Aggregates: Deduction and Prediction of the Stress-Strain. Materials. 2016; 9(12):1029. https://doi.org/10.3390/ma9121029
Chicago/Turabian StyleCabrera-Covarrubias, Francisca Guadalupe, José Manuel Gómez-Soberón, Jorge Luis Almaral-Sánchez, Susana Paola Arredondo-Rea, María Consolación Gómez-Soberón, and Ramón Corral-Higuera. 2016. "An Experimental Study of Mortars with Recycled Ceramic Aggregates: Deduction and Prediction of the Stress-Strain" Materials 9, no. 12: 1029. https://doi.org/10.3390/ma9121029
APA StyleCabrera-Covarrubias, F. G., Gómez-Soberón, J. M., Almaral-Sánchez, J. L., Arredondo-Rea, S. P., Gómez-Soberón, M. C., & Corral-Higuera, R. (2016). An Experimental Study of Mortars with Recycled Ceramic Aggregates: Deduction and Prediction of the Stress-Strain. Materials, 9(12), 1029. https://doi.org/10.3390/ma9121029