Anion Effects on the Ion Exchange Process and the Deformation Property of Ionic Polymer Metal Composite Actuators
Abstract
:1. Introduction
2. Experimental Methods
2.1. Preparation of IPMC Actuators
2.2. Evaluation of Actuator Response to a Step Voltage
2.2.1. Experiment 1: Responses to a Step Voltage before Ion Exchange
2.2.2. Experiment 2: Responses to a Step Voltage after Ion Exchange
2.3. Alternating Current Impedance Measurements
2.3.1. Experiment 3: AC Impedance Measurements before Ion Exchange
2.3.2. Experiment 4: AC Impedance Measurements after Ion Exchange
3. Experimental Results
3.1. Deformation Behavior in Experiments 1 and 2
3.2. Alternating-Current Impedance Measurement
4. Discussion
4.1. Correlation between Characteristic Displacement and Other Parameters
4.2. Relationship between Ion Conductivity and Ion Exchange
4.3. Relationship between Parameters at the Cathode and Ion Exchange
4.4. The Relationship between Characteristic Displacement and Ion Exchange
5. Conclusions
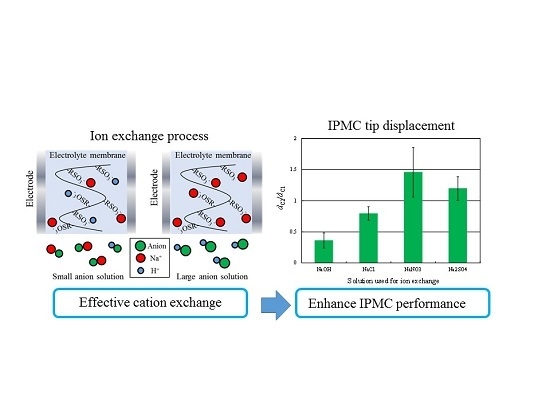
- In the response to 2-V step voltages, the use of smaller anions decreases the charge intensity, discharge intensity, and the characteristic displacement of the IPMC actuator. In contrast, larger anions increase the discharge intensity and characteristic displacement.
- The AC impedance measurement results indicate that smaller anions increase the charge transfer resistance at the cathode and decrease the double-layer capacitance at the cathode. Conversely, larger anions decrease the charge transfer resistance and increase the double-layer capacitance. Furthermore, the ion conductivity greatly increases after ion exchange in NaOH and NaCl solutions.
- The main effect of anion sizes is appeared in the ion exchange process. Anions hardly migrate into the Nafion membrane which has the negatively charged R-SO3− groups. Therefore, anions do not directly affect the deformation principle of IPMC actuators. We consider that anion sizes affect the cation exchange process and that the cation concentration in the membrane directly affects the deformation principle of IPMC actuators.
- When ion exchange was performed in solutions containing larger anions, the cation concentration in the membrane tended to increase. The resistance to hydrated cations migration was reduced under these conditions; thus, the extent to which ion conductivity was increased by ion exchange became large, as did the double-layer capacitance at the cathode. These changes following the ion exchange with solutions incorporating larger anions increased the tip displacement of the IPMCs.
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix
References
- Shahinpoor, M.; Kim, K.J. Ionic polymer-metal composites: I. Fundamentals. Smart Mater. Struct. 2001, 10, 819–833. [Google Scholar] [CrossRef]
- Pugal, D.; Jung, K.; Aabloo, A.; Kim, K.J. Ionic polymer-metal composite mechanoelectrical transduction: Review and perspectives. Polym. Int. 2010, 59, 279–289. [Google Scholar] [CrossRef]
- Tiwari, R.; Garcia, E. The state of understanding of ionic polymer metal composite architecture: A review. Smart Mater. Struct. 2011, 20. [Google Scholar] [CrossRef]
- Carpi, F.; Kornbluh, R.; Sommer-Larsen, P.; Alici, G. Electroactive polymer actuators as artificial muscles: Are they ready for bioinspired applications? Bioinspir. Biomim. 2011, 6. [Google Scholar] [CrossRef] [PubMed]
- Onishi, K.; Sewa, S.; Asaka, K.; Fujiwara, N.; Oguro, K. Morphology of electrodes and bending response of the polymer electrolyte actuator. Electrochim. Acta 2000, 46, 737–743. [Google Scholar] [CrossRef]
- Shahinpoor, M.; Kim, K.J. The effect of surface-electrode resistance on the performance of ionic polymer-metal composite (IPMIC) artificial muscles. Smart Mater. Struct. 2000, 9, 543–551. [Google Scholar] [CrossRef]
- Enikov, E.T.; Seo, G.S. Experimental analysis of current and deformation of ion-exchange polymer metal composite actuators. Exp. Mech. 2005, 45, 383–391. [Google Scholar] [CrossRef]
- Kikuchi, K.; Tsuchitani, S. Nafion (R)-based polymer actuators with ionic liquids as solvent incorporated at room temperature. J. Appl. Phys. 2009, 106. [Google Scholar] [CrossRef]
- Shahinpoor, M.; Bar-Cohen, Y.; Simpson, J.O.; Smith, J. Ionic polymer-metal composites (IPMCs) as biomimetic sensors, actuators and artificial muscles—A review. Smart Mater. Struct. 1998, 9, 543–551. [Google Scholar] [CrossRef]
- Paquette, J.W.; Kim, K.J. Ionomeric electroactive polymer artificial muscle for naval applications. IEEE J. Ocean. Eng. 2004, 29, 729–737. [Google Scholar] [CrossRef]
- Bonomo, C.; Fortuna, L.; Giannone, P.; Graziani, S. A method to characterize the deformation of an IPMC sensing membrane. Sens. Actuators A Phys. 2005, 123–124, 146–154. [Google Scholar] [CrossRef]
- Bonomo, C.; Bruneto, P.; Fortuna, L.; Giannone, P.; Graziani, S.; Strazzeri, S. A tactile sensor for biomedical applications based on IPMCs. IEEE Sens. J. 2008, 8, 1486–1493. [Google Scholar] [CrossRef]
- Shahinpoor, M. Ionic polymeric conductor nanocomposites (IPCNCs) as distributed nanosensors and Nanoactuators. Bioinspir. Biomim. 2008, 3. [Google Scholar] [CrossRef] [PubMed]
- Di, P.G.; Fortuna, L.; Graziani, S.; La, R.M.; Nicolosi, D.; Sicurella, G.; Umana, E. All-organic motion sensors: Electromechanical modeling. IEEE Trans. Instrum. Meas. 2009, 58, 3731–3738. [Google Scholar]
- Krishen, K. Space applications for ionic polymer-metal composite sensors, actuators, and artificial muscles. Acta Astronaut. 2009, 64, 1160–1166. [Google Scholar] [CrossRef]
- Santos, J.; Lopes, B.; Branco, P.J.C. Ionic polymer-metal composite material as a diaphragm for micropump devices. Sens. Actuators A Phys. 2010, 161, 225–233. [Google Scholar] [CrossRef]
- Tiwari, R.; Kim, K.J. Disc-shaped ionic polymer metal composites for use in mechano-electrical applications. Smart Mater. Struct. 2010, 19. [Google Scholar] [CrossRef]
- Sareh, S.; Rossiter, J.; Conn, A.; Drescher, K.; Goldstein, R.E. Swimming like algae: Biomimetic soft artificial cilia. J. R. Soc. Interface 2013, 10. [Google Scholar] [CrossRef] [PubMed]
- Sareh, S.; Rossiter, J. Kirigami artificial muscles with complex biologically inspired morphologies. Smart Mater. Struct. 2013, 22. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Li, J.Y. Electromechanical response of ionic polymer-metal composites. J. Appl. Phys. 2000, 87, 3321–3331. [Google Scholar] [CrossRef]
- Nemat-Nasser, S.; Wu, Y.X. Comparative experimental study of ionic polymer-metal composites with different backbone ionomers and in various cation forms. J. Appl. Phys. 2003, 93, 5255–5267. [Google Scholar] [CrossRef]
- Jung, K.; Nam, J.; Choi, H. Investigations on actuation characteristics of IPMC artificial muscle actuator. Sens. Actuators A Phys. 2003, 107, 183–192. [Google Scholar] [CrossRef]
- Jeon, J.H.; Yeom, S.W.; Oh, I.K. Fabrication and actuation of ionic polymer metal composites patterned by combining electroplating with electroless plating. Compos. Part A 2008, 39, 588–596. [Google Scholar] [CrossRef]
- Kim, S.M.; Kim, K.J. Palladium buffer-layered high performance ionic polymer-metal composites. Smart Mater. Struct. 2008, 17. [Google Scholar] [CrossRef]
- Chang, L.; Chen, H.; Zhu, Z.; Li, B. Manufacturing process and electrode properties of palladium-electroded ionic polymer-metal composite. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Noh, T.G.; Tak, Y.; Nam, J.D.; Choi, H. Electrochemical characterization of polymer actuator with large interfacial area. Electrochim. Acta 2002, 47, 2341–2346. [Google Scholar] [CrossRef]
- Kim, D.; Kim, K.J.; Nam, J.D.; Palmre, V. Electro-chemical operation of ionic polymer-metal composites. Sens. Actuators B Chem. 2011, 155, 106–113. [Google Scholar] [CrossRef]
- Nakamura, T.; Ihara, T.; Horiuchi, T.; Mukai, T.; Asaka, K. Measurement and modeling of electro-chemical properties of ion polymer metal composite by complex impedance analysis. SCIE J. Control Meas. Syst. Integr. 2009, 2, 373–378. [Google Scholar] [CrossRef]
- Palmre, V.; Pugal, D.; Kim, K.J.; Leang, K.K.; Asaka, K.; Aabloo, A. Nanothorn electrodes for ionic polymer-metal composite artificial muscles. Sci. Rep. 2014, 4. [Google Scholar] [CrossRef] [PubMed]
- Aoyagi, W.; Omiya, M. Mechanical and electrochemical properties of an IPMC actuator with palladium electrodes in acid and alkaline solutions. Smart Mater. Struct. 2013, 22. [Google Scholar] [CrossRef]
- Lee, J.W.; Yoo, Y.T. Anion effects in imidazolium ionic liquids on the performance of IPMCs. Sens. Actuators B Chem. 2009, 137, 539–546. [Google Scholar] [CrossRef]
- Fleming, M.J.; Kim, K.J.; Leang, K.K. Mitigating IPMC back relaxation through feedforward and feedback control of patterned electrodes. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Kobayashi, T.; Omiya, M. Deformation behaviors of ionic-polymer-metal composite actuator with palladium electrodes for various solvents, temperatures, and frequencies. Smart Mater. Struct. 2012, 21. [Google Scholar] [CrossRef]
- Bennett, M.D.; Leo, D.J.; Wilkes, G.L.; Beyer, F.L.; Pechar, T.W. A model of charge transport and electromechanical transduction in ionic liquid-swollen Nafion membranes. Polymer 2004, 47, 6782–6796. [Google Scholar] [CrossRef]
- Paquette, J.W.; Kim, K.J.; Nam, J.D.; Tak, Y.S. An Equivalent Circuit Model for Ionic Polymer-metal Composites and Their Performance Improvement by a Clay-based Polymer Nano-composite Technique. J. Intell. Mater. Syst. Struct. 2003, 14, 633–642. [Google Scholar] [CrossRef]
- Ma, S.; Kuse, A.; Siroma, Z.; Yasuda, K. Measuring conductivity of proton conductive membranes in the direction of thickness. ESPEC Corp. Technol. Rep. 2005, 20, 12–20. [Google Scholar]
- Gierke, T.D. The morphology in nafion perfluorinated membrane products, as determined by wide- and small-angle X-ray studies. J. Polym. Sci. Part B Polym. Phys. 1981, 19, 1687–1704. [Google Scholar] [CrossRef]
- Skarda, V.; Rais, J.; Kyrs, M. Hydration of alkali metal cations and protons in polar organic solvents. J. Inorg. Nucl. Chem. 1979, 41, 1443–1446. [Google Scholar] [CrossRef]
- Sata, T. Ion Exchange Membranes: Preparation, Characterization, Modification and Application; The Royal Society of Chemistry: Cambridge, UK, 2004; pp. 10–13. [Google Scholar]
- Inamuddin, Dr.; Mohammad, L. (Eds.) Ion Exchange Technology I Theory and Materials; Springer: Dordrecht, The Netherlands, 2012; pp. 59–60.
- Israelachvili, J. Intermolecular and Surface Forces, 3rd ed.; Academic Press: Cambridge, MA, USA, 2011; p. 79. [Google Scholar]
- Kielland, J. Individual activity coefficients of ions in aqueous solutions. J. Am. Chem. Soc. 1937, 59, 1675–1678. [Google Scholar] [CrossRef]






| Solution | NaOH aq | NaCl aq | NaNO3 aq | Na2SO4 aq |
|---|---|---|---|---|
| Concentration (mol/L) | 0.1 | 0.1 | 0.1 | 0.05 |
| Parameters | NaOH | NaCl | NaNO3 | Na2SO4 | COR |
|---|---|---|---|---|---|
| dC2/dC1 | 0.361 | 0.794 | 1.458 | 1.196 | – |
| Qin2/Qin1 | 0.521 | 0.773 | 1.009 | 1.040 | 0.961 |
| Qout2/Oout1 | 0.366 | 0.710 | 1.214 | 1.405 | 0.921 |
| σ4/σ3 | 1.065 | 1.123 | 1.664 | 1.365 | 0.935 |
| R14/R13 | 1.197 | 0.437 | 0.930 | 1.122 | −0.067 |
| C14/C13 | 0.908 | 0.861 | 0.599 | 1.098 | −0.348 |
| R24/R23 | 0.878 | 1.772 | 0.391 | 0.649 | −0.513 |
| C24/C23 | 0.873 | 0.799 | 1.101 | 1.142 | 0.795 |
© 2016 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC-BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aoyagi, W.; Omiya, M. Anion Effects on the Ion Exchange Process and the Deformation Property of Ionic Polymer Metal Composite Actuators. Materials 2016, 9, 479. https://doi.org/10.3390/ma9060479
Aoyagi W, Omiya M. Anion Effects on the Ion Exchange Process and the Deformation Property of Ionic Polymer Metal Composite Actuators. Materials. 2016; 9(6):479. https://doi.org/10.3390/ma9060479
Chicago/Turabian StyleAoyagi, Wataru, and Masaki Omiya. 2016. "Anion Effects on the Ion Exchange Process and the Deformation Property of Ionic Polymer Metal Composite Actuators" Materials 9, no. 6: 479. https://doi.org/10.3390/ma9060479
APA StyleAoyagi, W., & Omiya, M. (2016). Anion Effects on the Ion Exchange Process and the Deformation Property of Ionic Polymer Metal Composite Actuators. Materials, 9(6), 479. https://doi.org/10.3390/ma9060479