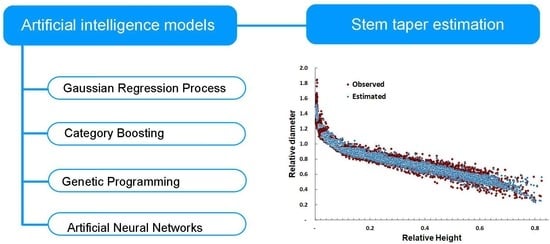
Do AI Models Improve Taper Estimation? A Comparative Approach for Teak
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Data and Data Preprocessing
2.3. Artificial Intelligence Models
2.3.1. Genetic Programming
2.3.2. Gaussian Process Regression (GPR)
2.3.3. Category Boosting (CatBoost)
2.3.4. Artificial Neural Networks (ANN)
2.4. Non-Linear Regression Models
2.5. Goodness of Fit of the Models
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Perez, D. Growth and Volume Equations Developed from Stem Analysis for Tectona Grandis in Costa Rica. J. Trop. For. Sci. 2008, 20, 66–75. [Google Scholar]
- Moret, A.; Jerez, M.; Mora, A. Determinación de Ecuaciones de Volumen Para Plantaciones de Teca (Tectona Grandis L.) En La Unidad Experimental de La Reserva Forestal Caparo, Estado Barinas–Venezuela. Rev. For. Venez. 1998, 42, 41–50. [Google Scholar]
- CONAFOR www.gob.mx/conafor/. Available online: https://www.gob.mx/conafor/documentos/plantaciones-forestales-comerciales-27940/ (accessed on 1 July 2020).
- Kozak, A. My Last Words on Taper Equations. For. Chron. 2004, 80, 507–515. [Google Scholar] [CrossRef]
- Fang, Z.; Borders, B.E.; Bailey, R.L. Compatible Volume-Taper Models for Loblolly and Slash Pine Based on a System with Segmented-Stem Form Factors. For. Sci. 2000, 46, 1–12. [Google Scholar]
- Quiñonez-Barraza, G.; los Santos-Posadas, D.; Héctor, M.; Álvarez-González, J.G.; Velázquez-Martínez, A. Sistema Compatible de Ahusamiento y Volumen Comercial Para Las Principales Especies de Pinus En Durango, México. Agrociencia 2014, 48, 553–567. [Google Scholar]
- Pompa-García, M.; Corral-Rivas, J.J.; Ciro Hernández-Díaz, J.; Alvarez-González, J.G. A System for Calculating the Merchantable Volume of Oak Trees in the Northwest of the State of Chihuahua, Mexico. J. For. Res. 2009, 20, 293–300. [Google Scholar] [CrossRef]
- Cruz-Cobos, F.; los Santos-Posadas, D.; Héctor, M.; Valdez-Lazalde, J.R. Sistema Compatible de Ahusamiento-Volumen Para Pinus Cooperi Blanco En Durango, México. Agrociencia 2008, 42, 473–485. [Google Scholar]
- Tamarit, U.J.C.; De los Santos Posadas, H.M.; Aldrete, A.; Valdez Lazalde, J.R.; Ramírez Maldonado, H.; Guerra De la Cruz, V. Sistema de Cubicación Para Árboles Individuales de Tectona Grandis L. f. Mediante Funciones Compatibles de Ahusamiento-Volumen. Rev. Mex. Cienc. For. 2014, 5, 58–74. [Google Scholar]
- Schikowski, A.B.; Corte, A.P.; Ruza, M.S.; Sanquetta, C.R.; Montano, R.A. Modeling of Stem Form and Volume through Machine Learning. An. Acad. Bras. Cienc. 2018, 90, 3389–3401. [Google Scholar] [CrossRef] [PubMed]
- Nunes, M.H.; Görgens, E.B. Artificial Intelligence Procedures for Tree Taper Estimation within a Complex Vegetation Mosaic in Brazil. PLoS ONE 2016, 11, e0154738. [Google Scholar] [CrossRef]
- Sakici, O.; Ozdemir, G. Stem Taper Estimations with Artificial Neural Networks for Mixed Oriental Beech and Kazdaği Fir Stands in Karabük Region, Turkey. Cerne 2018, 24, 439–451. [Google Scholar] [CrossRef]
- Socha, J.; Netzel, P.; Cywicka, D. Stem Taper Approximation by Artificial Neural Network and a Regression Set Models. Forest 2020, 11, 79. [Google Scholar] [CrossRef]
- Koza, J.R. Introduction to Genetic Programming. In Proceedings of the 9th Annual Conference Companion on Genetic and Evolutionary Computation, London, UK, 7–11 July 2007; pp. 3323–3365. [Google Scholar]
- Rasmussen, C.E. Gaussian Processes for Machine Learning. In Summer School Machine Learning; Springer: Berlin/Heidelberg, Germany, 2003; pp. 63–71. [Google Scholar]
- Jamei, M.; Ahmadianfar, I.; Olumegbon, I.A.; Karbasi, M.; Asadi, A. On the Assessment of Specific Heat Capacity of Nanofluids for Solar Energy Applications: Application of Gaussian Process Regression (GPR) Approach. J. Energy Storage 2021, 33, 102067. [Google Scholar] [CrossRef]
- Samarasinghe, M.; Al-Hawani, W. Short-Term Forecasting of Electricity Consumption Using Gaussian Processes. Master’s Thesis, University of Agder, West Agdelshire, Norway, 2012. [Google Scholar]
- Williams, C.K.; Rasmussen, C.E. Gaussian Processes for Machine Learning; MIT Press: Cambridge, MA, USA, 2006; Volume 2, No. 3; p. 4. [Google Scholar]
- Prokhorenkova, L.; Gusev, G.; Vorobev, A.; Dorogush, A.V.; Gulin, A. CatBoost: Unbiased Boosting with Categorical Features. Adv. Neural Inf. Process. Syst. 2018, 31, 6638–6648. [Google Scholar]
- R Foundation for Statistical Computing. R Core Team: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Haykin, S.; Lippmann, R. Neural Networks, A Comprehensive Foundation. Int. J. Neural Syst. 1994, 5, 363–364. [Google Scholar]
- Basheer, I.A.; Hajmeer, M. Artificial Neural Networks: Fundamentals, Computing, Design, and Application. J. Microbiol. Methods 2000, 43, 3–31. [Google Scholar] [CrossRef]
- Esmaeelzadeh, S.R.; Adib, A.; Alahdin, S. Long-Term Streamflow Forecasts by Adaptive Neuro-Fuzzy Inference System Using Satellite Images and K-Fold Cross-Validation (Case Study: Dez, Iran). KSCE J. Civ. Eng. 2015, 19, 2298–2306. [Google Scholar] [CrossRef]
- Borders, B.E. Systems of Equations in Forest Stand Modeling. For. Sci. 1989, 35, 548–556. [Google Scholar]
- Durbin, J.; Watson, G.S. Testing for Serial Correlation in Least Squares Regression. I; Oxford University Press: Oxford, UK, 1992; pp. 237–259. [Google Scholar]





| Variable | Maximum | Mean | Minimum | Standard deviation |
|---|---|---|---|---|
| Normal diameter D with bark (cm) | 45.00 | 26.89 | 8.50 | 6.81 |
| Total height H of the tree (m) | 27.00 | 18.96 | 9.03 | 3.39 |
| Commercial height (Hc) of the tree (m) | 18.15 | 10.82 | 2.62 | 2.60 |
| Age (years) | 22.00 | 15.99 | 7.5 | 4.62 |
| Parameter | Characteristic |
|---|---|
| Size of the population | 500 individuals |
| Criterion of finishing | 100 generations |
| Maximum size of the tree | 150 nodes, 12 levels |
| Elites | 1 individual |
| Parent selection | Selection per tournament |
| Cross | Sub-tree, 90% of probability |
| Mutation | 15% of mutation rate |
| Function of evaluation | Coefficient of determination R2 |
| Symbolic functions | (+, −, ×, ÷, exp, log) |
| Symbolic terminals | Constant, weight × variable |
| Model | Expression | Number of Equation |
|---|---|---|
| Fang 2000 | I1 = 1 if p1 ≤ z ≤ p2 otherwise I1 = 0 I2 = 1 if p2 ≤ z ≤ 1 otheriwse I2 = 0 | (9) |
| Kozak 2004 | b = 1.3/H | (10) |
| Model | R2 | RMSE (cm) | MBE (cm) | MAE (cm) | DW |
|---|---|---|---|---|---|
| Kozak2004 | 0.985 | 1.070 | −0.063 | 0.746 | 2.055 |
| Fang2000 | 0.974 | 1.405 | −0.125 | 1.120 | 2.053 |
| CatBoost | 0.978 | 1.299 | −0.038 | 0.920 | - |
| GPR | 0.978 | 1.314 | −0.010 | 0.952 | - |
| ANN | 0.985 | 1.085 | −0.082 | 0.751 | - |
| PG | 0.977 | 1.343 | −0.098 | 0.964 | - |
| Fang 2000 | Kozak 2004 | |||
|---|---|---|---|---|
| Parameter | Estimation | Standard Error | Estimation | Standard Error |
| a0 | 0.000068 | 2.181 × 10−8 | 1.223695 | 0.0385 |
| a1 | 1.928423 | 2.507 × 10−7 | 0.990858 | 0.0063 |
| a2 | 0.854570 | 0.08590 | −0.05868 | 0.0132 |
| b1 | 2.259 × 10−6 | 2.181 × 10−8 | 0.124234 | 0.0546 |
| b2 | 9.93 × 10−6 | 2.507 × 10−7 | −1.10823 | 0.0765 |
| b3 | 0.000034 | 2.264 × 10−7 | 0.406955 | 0.0151 |
| b4 | - | - | 7.265247 | 0.5388 |
| b5 | - | - | 0.113903 | 0.00364 |
| b6 | - | - | −0.44487 | 0.0393 |
| p1 | 0.016437 | 0.000183 | - | - |
| p2 | 0.082406 | 0.00205 | - | - |
| 0.507385 | 0.0173 | 0.413999 | 0.0158 | |
| 0.159728 | 0.0109 | 0.136901 | 0.0106 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fernández-Carrillo, V.H.; Quej-Chi, V.H.; De los Santos-Posadas, H.M.; Carrillo-Ávila, E. Do AI Models Improve Taper Estimation? A Comparative Approach for Teak. Forests 2022, 13, 1465. https://doi.org/10.3390/f13091465
Fernández-Carrillo VH, Quej-Chi VH, De los Santos-Posadas HM, Carrillo-Ávila E. Do AI Models Improve Taper Estimation? A Comparative Approach for Teak. Forests. 2022; 13(9):1465. https://doi.org/10.3390/f13091465
Chicago/Turabian StyleFernández-Carrillo, Víctor Hugo, Víctor Hugo Quej-Chi, Hector Manuel De los Santos-Posadas, and Eugenio Carrillo-Ávila. 2022. "Do AI Models Improve Taper Estimation? A Comparative Approach for Teak" Forests 13, no. 9: 1465. https://doi.org/10.3390/f13091465
APA StyleFernández-Carrillo, V. H., Quej-Chi, V. H., De los Santos-Posadas, H. M., & Carrillo-Ávila, E. (2022). Do AI Models Improve Taper Estimation? A Comparative Approach for Teak. Forests, 13(9), 1465. https://doi.org/10.3390/f13091465