Incorporation of Satellite Data and Uncertainty in a Nationwide Groundwater Recharge Model in New Zealand

Abstract

A nationwide model of groundwater recharge for New Zealand (NGRM), as described in this paper, demonstrated the benefits of satellite data and global models to improve the spatial definition of recharge and the estimation of recharge uncertainty. NGRM was inspired by the global-scale WaterGAP model but with the key development of rainfall recharge calculation on scales relevant to national- and catchment-scale studies (i.e., a 1 km × 1 km cell size and a monthly timestep in the period 2000–2014) provided by satellite data (i.e., MODIS-derived evapotranspiration, AET and vegetation) in combination with national datasets of rainfall, elevation, soil and geology. The resulting nationwide model calculates groundwater recharge estimates, including their uncertainty, consistent across the country, which makes the model unique compared to all other New Zealand estimates targeted towards groundwater recharge. At the national scale, NGRM estimated an average recharge of 2500 m${}^3$/s, or 298 mm/year, with a model uncertainty of 17%. Those results were similar to the WaterGAP model, but the improved input data resulted in better spatial characteristics of recharge estimates. Multiple uncertainty analyses led to these main conclusions: the NGRM model could give valuable initial estimates in data-sparse areas, since it compared well to most ground-observed lysimeter data and local recharge models; and the nationwide input data of rainfall and geology caused the largest uncertainty in the model equation, which revealed that the satellite data could improve spatial characteristics without significantly increasing the uncertainty. Clearly the increasing volume and availability of large-scale satellite data is creating more opportunities for the application of national-scale models at the catchment, and smaller, scales. This should result in improved utility of these models including provision of initial estimates in data-sparse areas. Topics for future collaborative research associated with the NGRM model include: improvement of rainfall-runoff models, establishment of snowmelt and river recharge modules, further improvement of estimates of rainfall and AET, and satellite-derived AET in irrigated areas. Importantly, the quantification of uncertainty, which should be associated with all future models, should give further impetus to field measurements of rainfall recharge for the purpose of model calibration.

1. Introduction

Satellite data have been shown to be important for global-scale assessments of water cycle variables, such as rainfall (GPM:[1]), evapotranspiration (ET) [2,3] and groundwater [4]. Global-scale hydrological models are increasingly used to characterise Earth’s groundwater [5,6,7], its fluxes [8,9] and its depletion [10]. Applications of these data and models will become more important with predictions for more climate extremes (i.e., droughts [11] and floods [12]) and consequent pressures on agricultural production and hazard response.

Global-scale satellite data and hydrological models are mostly spatially coarse (typically with grid resolutions of hundreds of square kilometres) and therefore lack the reliability for application at smaller scales. High-resolution data are often needed to cover the diversity of landscapes and climates, such as occurring in countries like New Zealand, where mean annual rainfall can differ from approximately 0.5 to 10 m over relatively short distances and groundwater fluxes are highly variant over the nation.

Studies in spatially diverse climates have shown applicability of higher-resolution satellite data in national or catchment-scale parametrisation of ET. MODIS-based ET (with a resolution of approximately 1 km${}^2$) was shown to be useful at the national scale of New Zealand [13] and Taiwan [14], and at the catchment scale, e.g., in Chili [15] and India [16]. A recent study in Greece also showed that MODIS based ET showed comparable results to modelled AET [17]. The well-known Landsat and Sentinel-2 satellite missions show applicability for more spatially refined (i.e., 100 m${}^2$ grid resolution) ET estimates [18,19].

High-resolution satellite ET data might increase capability of global-scale models (e.g., groundwater recharge) towards application at the national or catchment scale. Because that data-model combination provides large coverage with high spatial resolution, potential benefits include: increasing the spatial resolution of global-scale models; filling the gaps in areas where ground observations are sparse; and providing consistency to better address trans-boundary issues. Trans-boundary issues can occur if water allocation policies are not compatible across boundaries because neighbouring regions use differing data standards and models to assess allocation. The incorporation of higher resolution satellite data into global-scale models should improve understanding of global-scale model behaviour, but might also better assess uncertainty of local-scale models: as most models are calibrated in their local environment, not much is known about their uncertainty, especially near or beyond the boundaries of study areas that are smaller than a whole catchment.

In New Zealand, regional councils are responsible for policy on water allocation. Regional boundaries generally follow catchment boundaries. Groundwater recharge is often a key input to set allocation limits. National guideline limits for groundwater allocation with respect to recharge exist [20,21], but policy and the subsequent recharge assessments are managed at the regional scale. Development of a high-quality national assessment of groundwater resources, including recharge, is challenging. This is because recharge models are inconsistent across regions, partly because of the geography of the country, which includes high mountain ranges and large areas of recent volcanic deposits. To date, New Zealand does not have this consistent nationwide characterisation of groundwater recharge. Therefore, calculation of national-scale groundwater recharge is a key challenge for water resource management. The lack of such a nationwide approach hinders further scientific advances in national hydrological modelling. For example, the New Zealand national surface water model [22] could benefit from better information of groundwater fluxes, such as recharge.

Global recharge models are equipped to cover large areas and could thus fulfill the need for national recharge information. Incorporation of higher-resolution data into these models, e.g., satellite data or national datasets, might further improve the spatial characterisation of those global models. Incorporation of global models with high-resolution data might better the effect of spatial coarseness of those global models.

Uncertainty has not typically been assessed by groundwater recharge models in New Zealand. Most recharge models in New Zealand are some form of soil water balance [23,24,25], where differences can be caused by their different model equations (e.g., derivations of actual ET and rainfall-runoff ratios) or their input data. The impact of recharge uncertainty was demonstrated by White et al. [25], who used three groundwater recharge models for the Central Plains of Canterbury, New Zealand. They showed that estimated groundwater use as a percentage of recharge was highly model-dependent, and because of that dependency varied in between 63% and 80% in a relatively dry year. Another study in New Zealand [26] showed that the difference in three groundwater recharge models applied in one region was most likely caused by the inconsistency of input data and not by the differences in model equations. Groundwater recharge models in New Zealand would therefore highly benefit from a better uncertainty assessment.

This paper describes the calculation of a nationwide model of groundwater recharge from rainfall for New Zealand that incorporates MODIS satellite data of ET and vegetation alongside other national input datasets and is inspired by the global-scale WaterGAP recharge model [8]. The resulting nationwide model calculates groundwater recharge estimates, including their uncertainty, consistent across the country. The principal aim of this research is to assess the applicability of satellite data to downscale global-scale models, i.e., to national and catchment scales. The results are evaluated with local models and ground observations and an analyses of the inherent model equation uncertainty. This paper concludes with a discussion on future research topics, e.g., the advantage that satellite data brings to estimate irrigated areas; recommendations for improved model assumptions; and the need for collaborative research on the topic of groundwater recharge.

2. Method

2.1. General Description

The model in this study is called the Nationwide Groundwater Recharge Model (NGRM). The NGRM has a 1 km × 1 km model grid that covers most of New Zealand, in the national New Zealand Transverse Mercator (NZTM) projection. The NGRM applies monthly MODIS-derived satellite data of evapotranspiration, i.e., MOD16 [3,27]. Earlier studies calculated uncertainty of MOD16 data by taking into account the uncertainty of both ground observations and satellite data in the Penman and Penman-Monteith equations [13]. That uncertainty of MOD16 data was used as one of the inputs for the model uncertainty calculation. Additionally, satellite data of vegetation (MODIS C5 LAI/FPAR [28,29], Figure 1) were used to calculate interception. Satellite data are just one of many input in the NGRM, which also applies data from national databases of precipitation, topography, soil parameters, and geology (Figure 2). A detailed description of input components is in Appendix A.

The NGRM calculates rainfall recharge to groundwater in monthly time steps, currently covering the period of January 2000 to December 2014. The model uses a simple soil water balance: it calculates a mass balance between vertical water inflow and outflow in a simple representation of the soil (i.e., one layer), and it is assumed that any surplus water in the soil layer either drains to groundwater or goes to runoff. Other common soil water balance models are the groundwater recharge module in WaterGAP [8], USGS-SWB [24], Rushton [23]. The NGRM consists of a newly developed method and code, but is largely inspired by the approach of the WaterGAP model, that calculates an initial recharge and then uses several recharge correction factors, i.e., for slope, soil, geology and more. The strengths of the WaterGAP model are, in our opinion: it is a simple but rigorous method; it is a well described and accepted method; and it includes a deeper ‘geology’ layer.

The NGRM is uncalibrated. However, case study comparisons described within this article have been used to improve the nationwide model equations such that the model is considered to provide suitable estimates in these case studies.

2.2. Rainfall Recharge Model Equation

In monthly time steps, rainfall recharge R (in mm) was calculated for time step i as:

$$\begin{array}{c}\hfill R_i=[P_i{f}_{slope}-AE{T}_i-S_{i-1}]f_{soil}{f}_{geol};R_i>0,\end{array}$$

(1)

where:

• $P_i$ is surface rainfall (in mm, after correction for interception and snow);
• $f_{slope}$ is a correction factor for rainfall runoff due to slope [0 to 1];
• $AET$ is actual evapotranspiration (in mm);
• S is soil storage (mm);
• $f_{soil}$ is a correction factor for permeability of soil [0 to 1];
• $f_{geol}$ is a correction factor for the geology [0 to 1].

If $R_i$< 0, it is set to zero and the resulting storage deficit $S_i<S_{i-1}$ is used for the calculation of $R_{i+1}$. Appendix B gives a detailed description of pre-processing, model assumptions, and the assignment of correction factors of slope, soil and geology.

2.3. Uncertainty of Rainfall Recharge

From here onwards, ‘top-down’ uncertainty is defined as the NGRM model equation uncertainty; ‘bottom-up’ uncertainty is defined as the comparison of NGRM modelled output to ground observations or other (local) models.

Top-down uncertainty was calculated by error propagation of Equation (1), i.e., propagating the variance and covariance of all input components [30]:

$${{\sigma }_f}^2={\mathbf{g}}^T\mathbf{V}\mathbf{g}$$

(2)

where ${{\sigma }_f}^2$ is the variance of a function f, which has $n=1$:N input components; $\mathbf{V}$ is the variance-covariance matrix of all input components; $\mathbf{g}$ is a vector of input component $\partial f/\partial n_i$; and ${\mathbf{g}}^T$ is the transpose of $\mathbf{g}$. Appendix C describes the individual components of the variance-covariance matrix.

Top-down model uncertainties were compiled for further analyses. First, mean monthly and mean annual values for each model cell were compiled for comparison with ground-observed data and other local models. Second, NGRM recharge values were binned into simple histograms. Third, NGRM recharge values were binned into 100 bins in between the minimum and maximum recharge, where each bin was plotted against mean and standard deviation of top-down uncertainty per bin. Subsequently, individual model input components ($P_i$, $f_{slope}$, $AET$, S, $f_{soil}$ and $f_{geol}$) were binned and plotted against top-down uncertainty.

3. Results

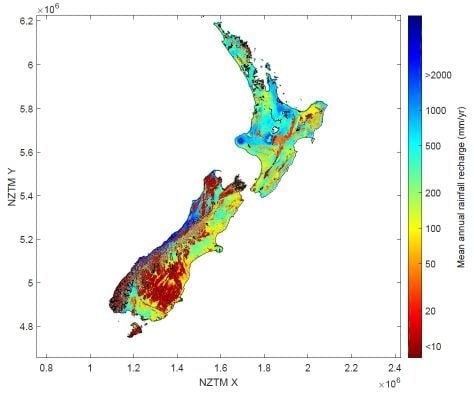
3.1. National Rainfall Recharge Estimates

Application of the NGRM leads to nationwide estimates of rainfall recharge at monthly intervals at 1 km × 1 km grid resolution (mean annual values shown in Figure 3). The time series of recharge and some model components for three (randomly chosen) locations are shown in Figure 4. Mean annual uncertainty is highest at places where rainfall is high (Figure 5, left). Uncertainty of geology plays a minor role in large aquifers, where the geology is permeable, because it does not constrain recharge in those areas. However, relative uncertainty, i.e., as a percentage of the mean annual recharge (Figure 5, right), is largest in areas where hydraulic conductivity is low, which is where the model equation is most sensitive to the high uncertainty of hydraulic conductivity (see Section 4 and Appendix B). Recharge uncertainty is thus affected by rainfall for its high volumes, but also sensitive to geology for its high uncertainty and significant role in the model equation.

The total New Zealand average rainfall recharge for the period 2000–2014 estimated from the NGRM model is 2500 m${}^3$/s, with a model uncertainty $\sigma$ of 17% (

Table 1. 2000–2014 mean rainfall recharge values of the NGRM compiled for New Zealand, the North Island and the South Island, including model uncertainty.

	m${}^3$/s	mm/year
New Zealand	2500 ± 414	298 ± 49
North Island	1334 ± 199	370 ± 55
South Island	1165 ± 212	243 ± 44

). Total rainfall recharge for the North Island is 1334 m${}^3$/s (a mean of 370 mm/year, $\sigma$ 15%); for the South Island it is 1166 m${}^3$/s (a mean of 243 mm/year, $\sigma$ 18%). The national estimate falls within the 2835 m${}^3$/s ($\sigma$ 10%) recharge estimate of the WaterGAP model [8]. Although that estimate is for a different period (1972–1990), rainfall in the two analysis periods is similar (1972 to 1990: 1881 mm/year; 2000–2014: 1839 mm/year).

The resulting recharge data of this study are available for the scientific community (NETCDF-CF1.6 format), through an open data licence (CC BY-NC 4.0: https://creativecommons.org/licenses/by-nc/4.0/), by contacting the authors.

3.2. Analyses of Binned Recharge and Top-Down Uncertainty

The mean recharge uncertainty has most values in between 0 and 10 mm/day, although maximum values occur up to 35 mm/day (Figure 6, left). Recharge uncertainty, relative to recharge, is highest for low values of recharge (Figure 6, right). Mean uncertainty for very low recharge can also be higher than 100% of the recharge value: although not plotted in Figure 6 (right), 26% of all uncertainty values are higher than their recharge (i.e., higher than 100%); and the mean uncertainty in between 0 and 1 mm/day recharge is over 200% of recharge. With increasing recharge, uncertainty diminishes to approximately 13% of recharge.

Figure 7 shows the behaviour of mean recharge and mean uncertainty per input component. In general, rainfall and geology play a dominant role on both recharge and uncertainty. This confirms the findings from Figure 5: in general, recharge according to the NGRM model is most sensitive to the underlying geology and rainfall (Figure 7, left axes). This analyses also shows that the NGRM model equation of recharge is most sensitive to rainfall when rainfall is less than 10 mm/day. Although other input components (AET, soil permeability, PAW and terrain slope) play a less dominant role, they still influence the recharge, e.g., for AET in between 0 and 2 mm/day mean recharge still shows considerable variation (Figure 7, top right). Recharge uncertainty ${\sigma }_R$ is also mostly depending on the geology and rainfall (Figure 7, right axes). The behaviour of ${\sigma }_R$ with increasing rainfall is different than that of recharge. Mean recharge uncertainty is higher than mean recharge over the whole range of $f_{geol}$, i.e., when geology limits recharge, uncertainty becomes significantly higher, also confirming earlier conclusions from Figure 5 (right).

3.3. Bottom-Up Uncertainty: Comparison of NGRM Recharge with Published Case Studies

NGRM recharge estimates were compared to lysimeters in the Canterbury Plains, New Zealand (Figure 8). These four dryland lysimeter stations, located in the plains (‘Airport’, ‘Hororata’, ‘Lincoln’, and ‘Winchmore’), have measured rainfall recharge from 1999 (or earlier) onwards. Hong and White [31] compared these lysimeter observations with two locally applied models (called SOILMOD/DRAIN and SMB-SMC and running at a daily time step) for the period 2000–2004. Mean annual NGRM rainfall recharge estimates for the same period are equal to rainfall recharge observations at three lysimeter stations (

Table 2. Mean annual rainfall recharge for July 2000–June 2004 for four Canterbury lysimeters stations and the NGRM model. All values are in mm/year.

Location	Lysimeter	NGRM
Airport	156	163 ± 23
Hororata	230	139 ± 27
Lincoln	68	67 ± 33
Winchmore	212	195 ± 25

and Figure 9): recharge values fall within the top-down uncertainty $\sigma$ at the Airport, Lincoln and Winchmore locations; at Hororata NGRM estimates much lower recharge, which is mainly caused by one anomalous rainfall event in January 2002 (Figure 10), where torrential rains occurred on the 1st of January, and heavy rain wreaked havoc and caused surface flooding along the east coast of Canterbury from 11–13 January [32,33]. The locally calibrated SOILMOD/DRAIN model handles this anomalous wet event better at Hororata than the NGRM and SMB-SMC model.

NGRM rainfall recharge estimates were compared to a locally calibrated model in the Waimakariri Canterbury Water Management Strategy Zone, New Zealand (Figure 11). The regional council, Environment Canterbury (ECAN), developed an advanced land surface recharge model with a grid resolution of 200 m for this area [35]. This ‘ECAN’ model was built with the MIKE-SHE hydrological platform [36]. The ECAN model gives mean recharge for the time period 1972–2015 for three different model scenarios: a minimum, average, and maximum land surface recharge scenario (Figure 12). The 2000–2013 mean annual recharge (196 ± 27 mm/year) agrees well with the ECAN model’s minimum (195 mm/year) scenario (

Table 3. Mean annual recharge for the Waimakariri catchment management zone model area (mm/year).

	NGRM	ECAN Min	ECAN Average	ECAN Max
Minimum	2	0	0	0
Maximum	432	661	661	664
Mean	196 ± 27	195	247	362
StDev of spatial distribution	110	126	127	120

). Comparing recharge for the two different time periods only creates a maximum estimation error of approximately 12 mm/year, since mean (VCS) rainfall for the model area for 1972–2013 was 798 mm/year; for 2000–2013 it was 763 mm/year; and rainfall recharge was in between approximately 0.25 and 0.45 of rainfall for the different scenarios. The spatial distributions of the mean annual recharge, quantified as a standard deviation, are similar for the NGRM and the ECAN models (110 mm/year for NGRM compared to approximately 125 mm/year for the three ECAN scenarios). However, there are visual spatial differences between the NGRM and the ECAN recharge models, of which the clearest difference is in river areas, where ECAN recharge is high and NGRM recharge is low. It seems likely that the ECAN model is more realistic than the NGRM in these areas, since the ECAN model uses local input data on soil. However, both models lead to the same mean annual recharge. To investigate which of the two models is best in which area requires more in-depth research that takes into account factors as: recharge in areas out of the model boundary, groundwater table depths; spring locations, and baseflow separation methods at multiple gauging locations in the rivers.

Recharge data were compared in the mid-Mataura catchment, located in the Southland Region, New Zealand (Figure 13). The area for this case study consists of five groundwater management zones. The groundwater flow model developed for the mid-Mataura catchment [37] used recharge values that were estimated for polygons with the Rushton method [23]. Mean annual recharge estimates between July 2000 and June 2007 of the NGRM and Rushton model in the five groundwater zones have been used for this comparison. Total mean annual NGRM recharge is lower than the Rushton estimate (131 ± 27 mm/year and 215 mm/year, respectively, see

Table 4. Mean annual rainfall and recharge for the Mid-Mataura model area (mm/year) for the NGRM and the Rushton model.

	NGRM	Rushton
Rainfall	809	903
Recharge	131 ± 27	215
RR ratio	0.16 ± 0.03	0.24

). This is partly caused by the difference in rainfall used for both models (809 mm/year for the NGRM model vs. 903 mm/year for the Rushton model). However, the ratio of recharge and rainfall of NGRM (0.16 ± 0.03) is still lower than the Rushton model (0.24). If Rushton and NGRM uncertainties would be similar, then recharge estimates NGRM would be 2$\sigma$ lower than the Rushton output. However, the Rushton polygons have an unknown but potentially large uncertainty, since there are so few polygons compared to the NGRM model cells (Figure 14). Rushton recharge estimates exclude areas outside the model boundaries that are still in the catchment. This could have implications for recharge occurring in areas in the catchment, but outside the model boundary (see discussion). Further local comparison should thus include an uncertainty estimate of the Rushton recharge, and should include the whole (sub-)catchment and not only the model boundary.

4. Discussion

4.1. Satellite Data to Better Constrain Uncertainty of the NGRM in Irrigated Areas

In irrigated areas, the soil storage receives an additional irrigated amount of water. This is only partly incorporated in the NGRM. The effect of irrigation and interception is taken into account by the AET, since the independent satellite-derived signal picks up vegetation health. Use of an independent satellite-derived signal is thus advantageous: it means that the AET is calculated as higher in these areas as the vegetation health has increased. Other parts of the model cannot always cope well with irrigation. For example, if irrigation is not fully efficient, (i.e., the water drains to groundwater instead of feeding the crop), the excess water will recharge and create an unknown bias in the monthly soil storage of the NGRM model. If water abstraction for irrigation comes from groundwater, the long-term effect of this excess irrigation recharge (a positive flux to recharge) will balance the water abstraction (a negative flux to recharge). However, if irrigation comes from surface water, this could impact both the monthly and the long term estimates of the NGRM recharge estimation. If national irrigation data become readily available, it is recommended to add these to the model equation. However, estimating exact volumes of irrigation is not straightforward and could result in other, much larger, bias of the model estimates. Use of the satellite-derived AET could help in better estimates of irrigated and non-irrigated areas. Furthermore, use of the MOD16 PET in a ratio of AET to PET could give a better, measured, indication of soil water deficit.

4.2. Limitations of the Model Equation and the Model Input Data

NGRM rainfall recharge estimates, including their underlying input satellite data of AET and vegetation, are a valuable new addition to existing national datasets of terrestrial water cycle variables [38,39,40]. For example, national water budgets based on long-term means can be aided by: estimates of baseflow using the long-term mean rainfall recharge; estimates of satellite-derived AET that include irrigation and interception; estimates of unrouted quickflow using the surface runoff that is stored by the model; and estimates of rainfall that are corrected for terrain slope, interception, and snow. Theoretically, a water budget can be made using all NGRM data. However, we acknowledge that implementation of a national water budget requires a much larger effort. This is because of many reasons, of which most relate to either model equation limitations or model input data.

The NGRM model has model limitations, mostly due to its simplifications. Although NGRM matches case studies well in this paper, the model may be too simple in other (sub-)catchments. The NGRM is considered a simplified model that aims for: a national and inter-regional overview; relating differences in existing local models; and estimating rainfall recharge in unexplored territory. The modelled rainfall recharge and its uncertainty estimates are therefore also considered simplified, although recharge estimates and their uncertainty fit well to observed differences with measurements and other local models. Because the model has not been calibrated on a smaller scale, like local models, it has to use generic or simplified assumptions on, e.g., slope-runoff relations, snow correction, hydraulic conductivity and river recharge (see Appendix A). Although case study comparisons have been used to improve the nationwide model equations such that the model is considered to provide suitable estimates in these case studies, uncertainty in explored areas is still relatively unknown. For example, considerable uncertainty remains in mountainous areas. Despite mountain geology being relatively impermeable, substantial amounts of rainfall can still permeate into the ground in high-rainfall climates (e.g., Southern Alps, New Zealand [41], Taiwan [42], British Columbia, Canada [43]). However, the uncertainty of rainfall recharge in mountains is large, because of the large uncertainty of hydraulic conductivity estimates in the NGRM model equation (see Results) and the often unknown location and permeability of fractures and faults. Comparisons with locally calibrated recharge models in this research (Waimakariri and Mataura) show that the NGRM model estimates a low mean recharge (when uncertainty is not taken into account). These local models do not take into account recharge that occurs outside the model boundaries. Recharge in the foothills or in mountainous area is thus not taken into account in these models, since they are not within the model boundary. If recharge outside the model boundaries would occur in reality, but models do not take this into account, then those models could be applied or calibrated incorrectly. Local recharge models should therefore consider taking into account at least the scale of the whole catchment, including the foothills and mountains.

Current national input datasets might not be good enough for model application at the local scale. We considered that model input data of the NGRM model is much finer, and probably better, than that of the large-scale WaterGAP model. However, local application of the NGRM model should embed a careful consideration of the quality of model input data (as should every model). This paragraph discusses three important model input data components: rainfall, ET and soil. Rainfall: NGRM application at the local scale reveals bias in rainfall rather than uncertainty. For example, the national (VCS) rainfall data in a study in the Waipa River catchment of the Waikato region, New Zealand, had to be increased by 15% in order to make it fit with the values of three independent models [26]. Systematic errors or biases in model input components propagate differently from uncertainty as calculated by the NGRM model equations. ET: although MOD16 AET (2000–2013) compares better to lysimeter-derived AET (1999–2011) in the Canterbury Plains of New Zealand than the commonly used average 1960–2006 AET [40] (Figure 15), an earlier study [13] demonstrated that model ‘top-down’ uncertainty in daily Penman PET in New Zealand can be 10–40% and estimation to AET brings more uncertainty because soil moisture and vegetation health are not always well known. Soil: comparison of the NGRM with the ECAN model in the Waimakariri catchment (see Results) showed that land surface recharge of the ECAN model is much higher in the river. This is not caused by a shortcoming of the model equation (as the ECAN model also does not embed a river recharge model), but by the differences in available soil data. The ECAN recharge model uses a local, more spatially detailed, soil data set, which is not available at the national scale. These local data account better for recharge in the very permeable river areas.

4.3. Future Research

This discussion highlights the need for further research on application of adjusted large-scale models and satellite data on the national or regional scale. Future research for improvements in the NGRM model is summarised as:

• The added value of satellite-derived AET in irrigated areas;
• Model improvements on rainfall-runoff, river recharge, snow and snowmelt, soil heterogeneity, hydraulic conductivity;
• Better uncertainty assessment of national input data, such as rainfall and AET;
• Incorporation of larger (catchment-based) model boundaries in future local and regional recharge studies;
• The effect of mountain recharge to groundwater modelling in New Zealand;

The NGRM model is inspired by international, global-scale, research. However, application of the NGRM model at th regional scale requires further improvement of model equations, input data and uncertainty estimates, e.g., locally measured rainfall and ET. Future research should therefore include all available data, starting with the best available, i.e., data from regional councils. In data-sparse regions, the regional data could then be completed with nationwide data, including data from this study and national flow data and statistics (e.g., [38,40]). This recommended research can be best applied in a collaborative environment, with regional councils, national research organisations, and international researchers. In this context, all the mentioned topics of research lead to one overall recommendation, i.e., more and better collaboration between international research of large-scale models and data with national and regional stakeholders in the research fields of groundwater and surface water. International and national research funds should further stimulate this collaborative approach.

5. Conclusions

This paper developed an approach to use large-scale satellite data and global hydrological models to estimate rainfall recharge at the national scale, i.e., across all regions of New Zealand. The model, NGRM, is inspired by the global WaterGAP model, but uses higher resolution input data , i.e., MODIS derived ET and vegetation data and the available nationwide datasets on rainfall, elevation, soil and geology. The NGRM estimates 1 km × 1 km monthly nationwide rainfall recharge from January 2000 to December 2014. A valuable addition to the recharge estimation is the model uncertainty estimate (not typically output from previous rainfall recharge models in New Zealand), based on variance and covariance analyses and model sensitivity of input components in the model environment. The estimated total New Zealand average recharge of the NGRM model results compiles to approximately 2500 m${}^3$/s, or 298 mm/year, with a model uncertainty of 17%. Those results are similar to the WaterGAP model, but the improved input data results in much better spatial characteristics of recharge estimates. Total rainfall recharge for the North Island is 1334 m${}^3$/s (a mean of 370 mm/year, $\sigma$ 15%); for the South Island it is 1166 m${}^3$/s (a mean of 243 mm/year, $\sigma$ 18%).

Although the NGRM model is uncalibrated, its recharge estimates compare well to most local and regional lysimeter data and recharge models. From the case study comparisons it is concluded that the nationwide rainfall recharge model gives a valuable initial estimate when applied at the local or regional scale, and can thus also be used in areas as a valuable initial estimate in data-sparse areas. Local applications might require the model to be calibrated and, as with any model, it is therefore recommended to carefully consider the NGRM model limitations for local application.

This research also provides improved insights into the uncertainty of rainfall recharge models, including the role of recharge model input components. It shows that recharge is most sensitive to rainfall in areas where recharge is high, but that uncertainty in hydraulic conductivity plays an important role in areas where recharge is impeded by geology. Thus, the satellite data of ET and vegetation improve the spatial characteristics of the recharge model without adding significant uncertainty. This research also shows that the combined top-down and bottom-up approach gives a more insightful description of uncertainty and underlines the importance of the availability of ground observations. Future research topics for application of large-scale models at the smaller scale are recommended to focus on collaborative research between international and national researchers and regional water managers, thus covering all spatial scales. Topics for future research include, amongst others: the added value of satellite-derived AET in irrigated areas; improvement of estimates of rainfall and evapotranspiration; and the impact of fracture zones on rainfall recharge within mountainous areas.