Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes
Abstract
:1. Introduction
2. Data and Data Processing
2.1. GRACE Total Water Storage Data
2.2. Precipitation Data
3. Methods
3.1. Empirical Mode Decomposition
- Set , and set , where i is the index of IMF to be extracted
- Extract the i-th IMF
- Set , , where k is the index of iteration
- Identify all local extrema in
- Generate the upper and lower envelopes, and , of by cubic spline interpolation
- Calculate the mean value of upper and lower envelopes as
- Remove from
- Check whether satisfies properties of IMF, namely, the number of extrema and the number of zero crossings must either equal or differ at most by one, and at any point the mean value of the envelope defined by the local maxima and the envelope defined by the local minima is zero. If the properties are satisfied, define as the i-th IMF ; otherwise, set and go to Step 2b.
- Define the current residual and set
- Repeat Steps 2–3 until either the residual becomes a monotonic function, or the number of zero crossings and extrema is the same as that of the successive sifting step.
3.2. Breaking Point Detection
3.3. Event Coincidence Analysis
4. Results
4.1. EMD Results
4.2. TC and BP Results
4.3. ECA Results
5. Discussion
6. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
Abbreviations
| BP | Breakpoint |
| CSR | Center for Space Research |
| EMD | Empirical mode decomposition |
| ECA | Event coincidence analysis |
| GLDAS | Global Land Data Assimilation System |
| GPCP | Global Precipitation Climatology Project |
| GRACE | Gravity Recovery and Climate Experiment |
| IMF | Intrinsic mode function |
| Mascon | Mass concentration |
| JPL | Jet Propulsion Laboratory |
| LSM | Land surface model |
| PDSI | Palmer Drought Severity Index |
| SH | Spherical harmonic |
| SPI | Standardized Precipitation Index |
| TC | TWSA-climatology |
| TRMM | Tropical Rainfall Measuring Mission |
| TWS | Total water storage |
| TWSA | total water storage anomalies |
References
- Diffenbaugh, N.S.; Scherer, M. Observational and model evidence of global emergence of permanent, unprecedented heat in the 20th and 21st centuries. Clim. Chang. 2011, 107, 615–624. [Google Scholar] [CrossRef] [PubMed]
- D’Odorico, P.; Laio, F.; Ridolfi, L. Does globalization of water reduce societal resilience to drought? Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Coumou, D.; Rahmstorf, S. A decade of weather extremes. Nat. Clim. Chang. 2012, 2, 491–496. [Google Scholar] [CrossRef]
- Donat, M.G.; Lowry, A.L.; Alexander, L.V.; O’Gorman, P.A.; Maher, N. More extreme precipitation in the world’s dry and wet regions. Nat. Clim. Chang. 2016, 508–513. [Google Scholar] [CrossRef]
- Mazdiyasni, O.; AghaKouchak, A. Substantial increase in concurrent droughts and heatwaves in the United States. Proc. Natl. Acad. Sci. USA 2015, 112, 11484–11489. [Google Scholar] [CrossRef] [PubMed]
- Milly, P.C.D.; Wetherald, R.T.; Dunne, K.; Delworth, T.L. Increasing risk of great floods in a changing climate. Nature 2002, 415, 514–517. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Alexander, L.; Hegerl, G.C.; Jones, P.; Tank, A.K.; Peterson, T.C.; Trewin, B.; Zwiers, F.W. Indices for monitoring changes in extremes based on daily temperature and precipitation data. Wiley Interdiscip. Rev. Clim. Chang. 2011, 2, 851–870. [Google Scholar] [CrossRef]
- Hao, Z.; Singh, V.P. Drought characterization from a multivariate perspective: A review. J. Hydrol. 2015, 527, 668–678. [Google Scholar] [CrossRef]
- Sadegh, M.; Ragno, E.; AghaKouchak, A. Multivariate copula analysis toolbox (mvcat): Describing dependence and underlying uncertainty using a Bayesian framework. Water Resour. Res. 2017, 53, 5166–5183. [Google Scholar] [CrossRef]
- Riegger, J.; Tourian, M. Characterization of runoff-storage relationships by satellite gravimetry and remote sensing. Water Resour. Res. 2014, 50, 3444–3466. [Google Scholar] [CrossRef]
- Reager, J.; Famiglietti, J. Global terrestrial water storage capacity and flood potential using GRACE. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Reager, J.; Thomas, B.; Famiglietti, J. River basin flood potential inferred using GRACE gravity observations at several months lead time. Nat. Geosci. 2014, 7, 588–592. [Google Scholar] [CrossRef]
- Rodell, M.; Velicogna, I.; Famiglietti, J.S. Satellite-based estimates of groundwater depletion in India. Nature 2009, 460, 999–1002. [Google Scholar] [CrossRef] [PubMed]
- Sun, A.Y.; Green, R.; Swenson, S.; Rodell, M. Toward calibration of regional groundwater models using GRACE data. J. Hydrol. 2012, 422, 1–9. [Google Scholar] [CrossRef]
- Zhao, M.; Velicogna, I.; Kimball, J.S. Satellite observations of regional drought severity in the continental United States using GRACE-based terrestrial water storage changes. J. Clim. 2017, 30, 6297–6308. [Google Scholar] [CrossRef]
- Chen, J.L.; Famigliett, J.S.; Scanlon, B.R.; Rodell, M. Groundwater storage changes: Present status from GRACE observations. In Remote Sensing and Water Resources; Cazenave, A., Champollion, N., Benveniste, J., Chen, J., Eds.; Springer International Publishing: Berlin, Germany, 2016; pp. 207–227. [Google Scholar]
- Ramillien, G.; Famiglietti, J.S.; Wahr, J. Detection of continental hydrology and glaciology signals from GRACE: A review. Surv. Geophys. 2008, 29, 361–374. [Google Scholar] [CrossRef]
- Houborg, R.; Rodell, M.; Li, B.; Reichle, R.; Zaitchik, B.F. Drought indicators based on model-assimilated gravity recovery and climate experiment (GRACE) terrestrial water storage observations. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Zhao, M.; Velicogna, I.; Kimball, J.S. A global gridded dataset of grace drought severity index for 2002–14: Comparison with PDSI and SPEI and a case study of the Australia millennium drought. J. Hydrometeorol. 2017, 18, 2117–2129. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.; Chen, J.; Rodell, M.; Seneviratne, S.; Viterbo, P.; Wilson, C. Total basin discharge for the Amazon and Mississippi river basins from GRACE and a land-atmosphere water balance. Geophys. Res. Lett. 2005, 32. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Reedy, R.C.; Pool, D.R.; Save, H.; Long, D.; Chen, J.; Wolock, D.M.; Conway, B.D.; Winester, D. Hydrologic implications of grace satellite data in the Colorado River basin. Water Resour. Res. 2015, 51, 9891–9903. [Google Scholar] [CrossRef]
- Yeh, P.J.F.; Swenson, S.; Famiglietti, J.; Rodell, M. Remote sensing of groundwater storage changes in Illinois using the Gravity Recovery and Climate Experiment (GRACE). Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Sun, A.Y.; Green, R.; Rodell, M.; Swenson, S. Inferring aquifer storage parameters using satellite and in situ measurements: Estimation under uncertainty. Geophys. Res. Lett. 2010, 37. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.H.; Famiglietti, J.S.; Swenson, S.; Rodell, M. Uncertainty in global groundwater storage estimates in a total groundwater stress framework. Water Resour. Res. 2015, 51, 5198–5216. [Google Scholar] [CrossRef] [PubMed]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Uncertainty in evapotranspiration from land surface modeling, remote sensing, and GRACE satellites. Water Resour. Res. 2014, 50, 1131–1151. [Google Scholar] [CrossRef] [Green Version]
- Rodell, M.; Famiglietti, J.S.; Chen, J.L.; Seneviratne, S.I.; Viterbo, P.; Holl, S.; Wilson, C.R. Basin scale estimates of evapotranspiration using GRACE and other observations. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef]
- Castle, S.L.; Reager, J.T.; Thomas, B.F.; Purdy, A.J.; Lo, M.H.; Famiglietti, J.S.; Tang, Q. Remote detection of water management impacts on evapotranspiration in the Colorado River basin. Geophys. Res. Lett. 2016, 43, 5089–5097. [Google Scholar] [CrossRef]
- Richey, A.S.; Thomas, B.F.; Lo, M.H.; Reager, J.T.; Famiglietti, J.S.; Voss, K.; Swenson, S.; Rodell, M. Quantifying renewable groundwater stress with GRACE. Water Resour. Res. 2015, 51, 5217–5238. [Google Scholar] [CrossRef] [PubMed]
- Frappart, F.; Ramillien, G.; Biancamaria, S.; Mognard, N.M.; Cazenave, A. Evolution of high-latitude snow mass derived from the GRACE gravimetry mission (2002–2004). Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef] [Green Version]
- Schmidt, R.; Flechtner, F.; Meyer, U.; Neumayer, K.-H.; Dahle, C.; König, R.; Kusche, J. Hydrological signals observed by the GRACE satellites. Surv. Geophys. 2008, 29, 319–334. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Longuevergne, L.; Long, D. Ground referencing GRACE satellite estimates of groundwater storage changes in the California Central Valley, USA. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Mocko, D.; Huang, M.; Li, B.; Rodell, M.; Mitchell, K.E.; Cai, X.; Ek, M.B. Comparison and assessment of three advanced land surface models in simulating terrestrial water storage components over the United States. J. Hydrometeorol. 2017, 18, 625–649. [Google Scholar] [CrossRef]
- Khandu, K.; Forootan, E.; Schumacher, M.; Awange, J.L.; Müller Schmied, H. Exploring the influence of precipitation extremes and human water use on total water storage (TWS) changes in the Ganges-Brahmaputra-Meghna river basin. Water Resour. Res. 2016. [Google Scholar] [CrossRef]
- Crowley, J.W.; Mitrovica, J.X.; Bailey, R.C.; Tamisiea, M.E.; Davis, J.L. Land water storage within the Congo basin inferred from GRACE satellite gravity data. Geophys. Res. Lett. 2006. [Google Scholar] [CrossRef]
- Long, D.; Scanlon, B.R.; Longuevergne, L.; Sun, A.Y.; Fernando, D.N.; Himanshu, S. GRACE satellites monitor large depletion in water storage in response to the 2011 drought in Texas. Geophys. Res. Lett. 2013, 40, 3395–3401. [Google Scholar] [CrossRef] [Green Version]
- AghaKouchak, A.; Farahmand, A.; Melton, F.; Teixeira, J.; Anderson, M.; Wardlow, B.; Hain, C. Remote sensing of drought: Progress, challenges and opportunities. Rev. Geophys. 2015, 53, 452–480. [Google Scholar] [CrossRef]
- Yirdaw, S.Z.; Snelgrove, K.R.; Agboma, C.O. GRACE satellite observations of terrestrial moisture changes for drought characterization in the Canadian prairie. J. Hydrol. 2008, 356, 84–92. [Google Scholar] [CrossRef]
- Abelen, S.; Seitz, F.; Abarca-del-Rio, R.; Güntner, A. Droughts and floods in the La Plata basin in soil moisture data and GRACE. Remote Sens. 2015, 7, 7324–7349. [Google Scholar] [CrossRef]
- Humphrey, V.; Gudmundsson, L.; Seneviratne, S.I. Assessing global water storage variability from GRACE: Trends, seasonal cycle, subseasonal anomalies and extremes. Surv. Geophys. 2016, 37, 357–395. [Google Scholar] [CrossRef] [PubMed]
- Maeda, E.E.; Kim, H.; Aragão, L.E.; Famiglietti, J.S.; Oki, T. Disruption of hydroecological equilibrium in southwest Amazon mediated by drought. Geophys. Res. Lett. 2015, 42, 7546–7553. [Google Scholar] [CrossRef]
- Thomas, A.C.; Reager, J.T.; Famiglietti, J.S.; Rodell, M. A GRACE-based water storage deficit approach for hydrological drought characterization. Geophys. Res. Lett. 2014, 41, 1537–1545. [Google Scholar] [CrossRef]
- Long, D.; Shen, Y.; Sun, A.Y.; Hong, Y.; Longuevergne, L.; Yang, Y.; Li, B.; Chen, L. Drought and flood monitoring for a large karst plateau in southwest China using extended GRACE data. Remote Sens. Environ. 2014, 155, 145–160. [Google Scholar] [CrossRef]
- Frappart, F.; Ramillien, G.; Ronchail, J. Changes in terrestrial water storage versus rainfall and discharges in the Amazon basin. Int. J. Climatol. 2013, 33, 3029–3046. [Google Scholar] [CrossRef] [Green Version]
- Kusche, J.; Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L. Mapping probabilities of extreme continental water storage changes from space gravimetry. Geophys. Res. Lett. 2016, 43, 8026–8034. [Google Scholar] [CrossRef]
- Cheng, L.; AghaKouchak, A.; Gilleland, E.; Katz, R.W. Non-stationary extreme value analysis in a changing climate. Clim. Chang. 2014, 127, 353–369. [Google Scholar] [CrossRef]
- Gilleland, E.; Katz, R.W. New software to analyze how extremes change over time. Eos Trans. Am. Geophys. Union 2011, 92, 13–14. [Google Scholar] [CrossRef]
- Katz, R.W. Statistical methods for nonstationary extremes. In Extremes in a Changing Climate; Springer: Berlin, Germany, 2013; pp. 15–37. [Google Scholar]
- Mann, H.B. Nonparametric tests against trend. Econom. J. Econom. Soc. 1945, 245–259. [Google Scholar] [CrossRef]
- Yue, S.; Wang, C. The mann-kendall test modified by effective sample size to detect trend in serially correlated hydrological series. Water Resour. Manag. 2004, 18, 201–218. [Google Scholar] [CrossRef]
- Amiri, A.; Allahyari, S. Change point estimation methods for control chart postsignal diagnostics: A literature review. Qual. Reliab. Eng. Int. 2012, 28, 673–685. [Google Scholar] [CrossRef]
- Lund, R.; Wang, X.L.; Lu, Q.Q.; Reeves, J.; Gallagher, C.; Feng, Y. Changepoint detection in periodic and autocorrelated time series. J. Clim. 2007, 20, 5178–5190. [Google Scholar] [CrossRef]
- Chandola, V.; Banerjee, A.; Kumar, V. Anomaly detection: A survey. ACM Comput. Surv. 2009, 41. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Zeileis, A.; Culvenor, D. Phenological change detection while accounting for abrupt and gradual trends in satellite image time series. Remote Sens. Environ. 2010, 114, 2970–2980. [Google Scholar] [CrossRef]
- Verbesselt, J.; Zeileis, A.; Herold, M. Near real-time disturbance detection using satellite image time series. Remote Sens. Environ. 2012, 123, 98–108. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. A study of the characteristics of white noise using the empirical mode decomposition method. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 2004, 1597–1611. [Google Scholar] [CrossRef]
- Chen, C.-F.; Lai, M.-C.; Yeh, C.-C. Forecasting tourism demand based on empirical mode decomposition and neural network. Knowl. Based Syst. 2012, 26, 281–287. [Google Scholar] [CrossRef]
- Zhang, X.; Lai, K.K.; Wang, S.-Y. A new approach for crude oil price analysis based on empirical mode decomposition. Energy Econ. 2008, 30, 905–918. [Google Scholar] [CrossRef]
- Lee, T.; Ouarda, T. Prediction of climate nonstationary oscillation processes with empirical mode decomposition. J. Geophys. Res. Atmos. 2011, 116. [Google Scholar] [CrossRef]
- Rodell, M.; Houser, P.; Jambor, U.; Gottschalck, J.; Mitchell, K.; Meng, C.; Arsenault, K.; Cosgrove, B.; Radakovich, J.; Bosilovich, M. The global land data assimilation system. Bull. Am. Meteorol. Soc. 2004, 85, 381–394. [Google Scholar] [CrossRef]
- Landerer, F.W.; Swenson, S.C. Accuracy of scaled GRACE terrestrial water storage estimates. Water Resour. Res. 2012, 48. [Google Scholar] [CrossRef]
- Long, D.; Longuevergne, L.; Scanlon, B.R. Global analysis of approaches for deriving total water storage changes from GRACE satellites. Water Resour. Res. 2015, 51, 2574–2594. [Google Scholar] [CrossRef] [Green Version]
- Watkins, M.M.; Wiese, D.N.; Yuan, D.N.; Boening, C.; Landerer, F.W. Improved methods for observing Earth’s time variable mass distribution with GRACE using spherical cap mascons. J. Geophys. Res. Solid Earth 2015, 120, 2648–2671. [Google Scholar] [CrossRef]
- Save, H.; Bettadpur, S.; Tapley, B.D. High-resolution CSR GRACE mascons. J. Geophys. Res. Solid Earth 2016, 121, 7547–7569. [Google Scholar] [CrossRef]
- Scanlon, B.R.; Zhang, Z.; Save, H.; Wiese, D.N.; Landerer, F.W.; Long, D.; Longuevergne, L.; Chen, J. Global evaluation of new GRACE mascon products for hydrologic applications. Water Resour. Res. 2017, 52, 9412–9429. [Google Scholar] [CrossRef]
- Huffman, G.J.; Bolvin, D.T.; Nelkin, E.J.; Wolff, D.B.; Adler, R.F.; Gu, G.; Hong, Y.; Bowman, K.P.; Stocker, E.F. The TRMM multisatellite precipitation analysis (TMPA): Quasi-global, multiyear, combined-sensor precipitation estimates at fine scales. J. Hydrometeorol. 2007, 8, 38–55. [Google Scholar] [CrossRef]
- Rui, H.; Beaudoing, H. Readme Document for Global Land Data Assimilation System Version 2 (GLDAS-2) Products; NASA Goddard Earth Sciences: Washington, DC, USA, 2016. [Google Scholar]
- Vicente-Serrano, S.M.; Beguería, S.; López-Moreno, J.I. A multiscalar drought index sensitive to global warming: The standardized precipitation evapotranspiration index. J. Clim. 2010, 23, 1696–1718. [Google Scholar] [CrossRef]
- Sahoo, A.K.; Sheffield, J.; Pan, M.; Wood, E.F. Evaluation of the tropical rainfall measuring mission multi-satellite precipitation analysis (TMPA) for assessment of large-scale meteorological drought. Remote Sens. Environ. 2015, 159, 181–193. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- Siegmund, J.F.; Siegmund, N.; Donner, R.V. Coincalc—a new R package for quantifying simultaneities of event series. Comput. Geosci. 2017, 98, 64–72. [Google Scholar] [CrossRef]
- Oki, T.; Sud, Y. Design of total runoff integrating pathways (TRIP)—A global river channel network. Earth Interact. 1998, 2, 1–37. [Google Scholar] [CrossRef]
- Trabucco, A.; Zomer, R. Global Aridity Index (Global-Aridity) and Global Potential Evapo-Transpiration (Global-Pet) Geospatial Database; CGIAR Consortium for Spatial Information: Washington, DC, USA, 2009. [Google Scholar]
- EM-DATA. The International Disasters Database; Centre for Research on the Epidemiology of Disasters, Université Catholique de Louvain: Louvain-la-Neuve, Belgium, 2017. [Google Scholar]
- Chen, J.; Wilson, C.; Tapley, B.; Yang, Z.; Niu, G. 2005 drought event in the Amazon river basin as measured by GRACE and estimated by climate models. J. Geophys. Res. Solid Earth 2009, 114. [Google Scholar] [CrossRef]
- Chen, J.L.; Wilson, C.R.; Tapley, B.D. The 2009 exceptional Amazon flood and interannual terrestrial water storage change observed by GRACE. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Ronchail, J.; Frappart, F.; Lavado, W.; Santini, W.; Guyot, J.L. The major floods in the Amazonas river and tributaries (Western Amazon Basin) during the 1970–2012 period: A focus on the 2012 flood. J. Hydrometeorol. 2013, 14, 1000–1008. [Google Scholar] [CrossRef]
- Espinoza, J.C.; Marengo, J.A.; Ronchail, J.; Carpio, J.M.; Flores, L.N.; Guyot, J.L. The extreme 2014 flood in south-western Amazon basin: The role of tropical-subtropical South Atlantic SST gradient. Environ. Res. Lett. 2014, 9. [Google Scholar] [CrossRef] [Green Version]
- Lott, N.; Ross, T. 1.2 Tracking and Evaluating US Billion Dollar Weather Disasters, 1980–2005. Available online: https://www.ncdc.noaa.gov/monitoring-content/billions/docs/lott-and-ross-2006.pdf (accessed on 8 December 2017).
- Awange, J.; Forootan, E.; Kuhn, M.; Kusche, J.; Heck, B. Water storage changes and climate variability within the nile basin between 2002 and 2011. Adv. Water Resour. 2014, 73, 1–15. [Google Scholar] [CrossRef]
- Winsemius, H.; Savenije, H.; Van De Giesen, N.; Van Den Hurk, B.; Zapreeva, E.; Klees, R. Assessment of gravity recovery and climate experiment (GRACE) temporal signature over the Upper Zambezi. Water Resour. Res. 2006, 42. [Google Scholar] [CrossRef]
- Ahmed, M.; Sultan, M.; Wahr, J.; Yan, E. The use of GRACE data to monitor natural and anthropogenic induced variations in water availability across Africa. Earth-Sci. Rev. 2014, 136, 289–300. [Google Scholar] [CrossRef]
- Leblanc, M.; Tweed, S.; Van Dijk, A.; Timbal, B. A review of historic and future hydrological changes in the Murray-Darling basin. Glob. Planet. Chang. 2012, 80, 226–246. [Google Scholar] [CrossRef]
- Hoerling, M.; Eischeid, J.; Kumar, A.; Leung, R.; Mariotti, A.; Mo, K.; Schubert, S.; Seager, R. Causes and predictability of the 2012 Great Plains drought. Bull. Am. Meteorol. Soc. 2014, 95, 269–282. [Google Scholar] [CrossRef]
- Otkin, J.A.; Anderson, M.C.; Hain, C.; Svoboda, M.; Johnson, D.; Mueller, R.; Tadesse, T.; Wardlow, B.; Brown, J. Assessing the evolution of soil moisture and vegetation conditions during the 2012 United States flash drought. Agric. For. Meteorol. 2016, 218, 230–242. [Google Scholar] [CrossRef]
- Syed, T.H.; Famiglietti, J.S.; Rodell, M.; Chen, J.; Wilson, C.R. Analysis of terrestrial water storage changes from GRACE and GLDAS. Water Resour. Res. 2008, 44. [Google Scholar] [CrossRef]
- Sun, A.Y.; Chen, J.; Donges, J. Global terrestrial water storage connectivity revealed using complex climate network analyses. Nonlinear Process. Geophys. 2015, 22, 433–446. [Google Scholar] [CrossRef]
- Sun, A.Y. Predicting groundwater level changes using GRACE data. Water Resour. Res. 2013, 49, 5900–5912. [Google Scholar] [CrossRef]
- Zaitchik, B.F.; Rodell, M.; Reichle, R.H. Assimilation of GRACE terrestrial water storage data into a land surface model: Results for the Mississippi river basin. J. Hydrometeorol. 2008, 9, 535–548. [Google Scholar] [CrossRef]
- Eicker, A.; Schumacher, M.; Kusche, J.; Döll, P.; Schmied, H.M. Calibration/data assimilation approach for integrating GRACE data into the watergap global hydrology model (WGHM) using an ensemble Kalman filter: First results. Surv. Geophys. 2014, 35, 1285–1309. [Google Scholar] [CrossRef]
- Girotto, M.; De Lannoy, G.; Reichle, R.; Rodell, M. Assimilation of gridded GRACE terrestrial water storage observation for improving soil moisture and shallow groundwater estimates. Water Resour. Res. 2016, 52, 4164–4183. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Save, H.; McCullough, C. High-frequency terrestrial water storage signal capture via a regularized sliding window mascon product from GRACE. J. Geophys. Res. Solid Earth 2016, 121, 4014–4030. [Google Scholar] [CrossRef]
- Ramillien, G.; Frappart, F.; Gratton, S.; Vasseur, X. Sequential estimation of surface water mass changes from daily satellite gravimetry data. J. Geodesy 2015, 89, 259–282. [Google Scholar] [CrossRef]








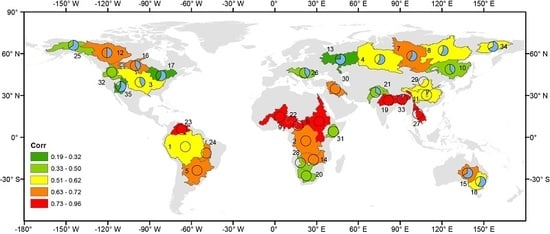
| ID | Basin | Area (×103 km2) | AI | Climate | Mean Period (mon) | P-TWSA Corr. | P-TWSA Lag (mon) | Coin-BP | Coin-TC | Irrig. (%) |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | Amazon | 6234 | 1.25 | H | 28 | 0.59 | 0 | 1 | 0.80 | 0.15 |
| 2 | Congo | 3759 | 0.89 | H | 24 | 0.65 | 0 | 0.86 | 0.61 | 0.01 |
| 3 | Mississippi | 3253 | 0.68 | H | 24 | 0.62 | −5 | 1 | 0.93 | 3.92 |
| 4 | Ob | 2997 | 0.76 | H | 33.6 | 0.53 | −7 | 1 | 1.00 | 0.23 |
| 5 | Parana | 2988 | 0.76 | H | 24 | 0.69 | 0 | 1 | 1.00 | 0.87 |
| 6 | Nile | 2978 | 0.34 | SA | 15.2 | 0.81 | 0 | 0.9 | 0.75 | 1.77 |
| 7 | Yenisei | 2609 | 0.88 | H | 21 | 0.72 | −7 | 1 | 1.00 | 0.03 |
| 8 | Lena | 2346 | 0.77 | H | 24 | 0.58 | −7 | 1 | 0.89 | 0 |
| 9 | Niger | 2124 | 0.34 | SA | 24 | 0.95 | 0 | 1 | 0.56 | 0.18 |
| 10 | Amur | 1868 | 0.83 | H | 24 | 0.50 | −5 | 1 | 1.00 | 2.04 |
| 11 | Yangtze | 1831 | 1.01 | H | 24 | 0.55 | −1 | NA | 0.88 | 8.4 |
| 12 | MacKenzie | 1740 | 0.76 | H | 42 | 0.66 | −6 | 1 | 0.87 | 0 |
| 13 | Volga | 1407 | 0.89 | H | 24 | 0.32 | −9 | 1 | 0.92 | 0.5 |
| 14 | Zambezi | 1341 | 0.55 | SH | 21 | 0.67 | 0 | 1 | 0.80 | 0.3 |
| 15 | Lake Eyre | 1248 | 0.13 | A | 18.7 | 0.66 | −8 | 1 | 0.63 | 0 |
| 16 | Nelson | 1110 | 0.67 | H | 21 | 0.65 | −5 | 1 | 0.92 | 0.6 |
| 17 | St. Lawrence | 1109 | 1.1 | H | 33.6 | 0.25 | −7 | 1 | 0.55 | 0.48 |
| 18 | Murray Darling | 1070 | 0.36 | SA | 24 | 0.60 | −7 | 1 | 0.90 | 2.46 |
| 19 | Ganges | 1032 | 0.73 | H | 28 | 0.89 | 0 | 1 | 0.84 | 30.62 |
| 20 | Orange | 999 | 0.22 | SA | 28 | 0.42 | 0 | 1 | 0.90 | 0.63 |
| 21 | Indus | 971 | 0.39 | SA | 24 | 0.41 | −4 | 1 | 0.65 | 22.71 |
| 22 | Chari | 925 | 0.4 | SA | 21 | 0.96 | 0 | 1 | 0.72 | 0.13 |
| 23 | Orinoco | 912 | 1.34 | H | 21 | 0.83 | 0 | 1 | 1.00 | 0.94 |
| 24 | Tocantins | 876 | 0.99 | H | 24 | 0.69 | 0 | 1 | 1.00 | 0.21 |
| 25 | Yukon | 851 | 0.69 | H | 28 | 0.50 | −8 | 1 | 0.52 | 0 |
| 26 | Danube | 806 | 0.91 | H | 33.6 | 0.41 | −5 | 1 | 1.00 | 4.78 |
| 27 | Mekong | 804 | 0.99 | H | 24 | 0.88 | 0 | 1 | 0.93 | 3.77 |
| 28 | Okavango | 793 | 0.29 | SA | 33.6 | 0.50 | 0 | 1 | 0.76 | 0.02 |
| 29 | Yellow | 786 | 0.52 | SH | 21 | 0.57 | 0 | 1 | 0.67 | 9.19 |
| 30 | Euphrates | 762 | 0.27 | SA | 21 | 0.67 | 0 | 1 | 0.97 | 10.15 |
| 31 | Juba | 741 | 0.26 | SA | 15.3 | 0.43 | 0 | 1 | 0.84 | 0.17 |
| 32 | Columbia | 722 | 0.78 | H | 33.6 | 0.45 | 0 | 1 | 0.67 | 3.98 |
| 33 | Bramaputra | 657 | 1.19 | H | 28 | 0.79 | −1 | 1 | 0.92 | 6.55 |
| 34 | Kolyma | 640 | 0.75 | H | 28 | 0.56 | −8 | 1 | 0.96 | 0 |
| 35 | Colorado | 636 | 0.27 | SA | 24 | 0.19 | −7 | 1 | 0.58 | 2.27 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, A.Y.; Scanlon, B.R.; AghaKouchak, A.; Zhang, Z. Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes. Remote Sens. 2017, 9, 1287. https://doi.org/10.3390/rs9121287
Sun AY, Scanlon BR, AghaKouchak A, Zhang Z. Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes. Remote Sensing. 2017; 9(12):1287. https://doi.org/10.3390/rs9121287
Chicago/Turabian StyleSun, Alexander Y., Bridget R. Scanlon, Amir AghaKouchak, and Zizhan Zhang. 2017. "Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes" Remote Sensing 9, no. 12: 1287. https://doi.org/10.3390/rs9121287
APA StyleSun, A. Y., Scanlon, B. R., AghaKouchak, A., & Zhang, Z. (2017). Using GRACE Satellite Gravimetry for Assessing Large-Scale Hydrologic Extremes. Remote Sensing, 9(12), 1287. https://doi.org/10.3390/rs9121287