Measuring Landscape Albedo Using Unmanned Aerial Vehicles
Abstract
:1. Introduction
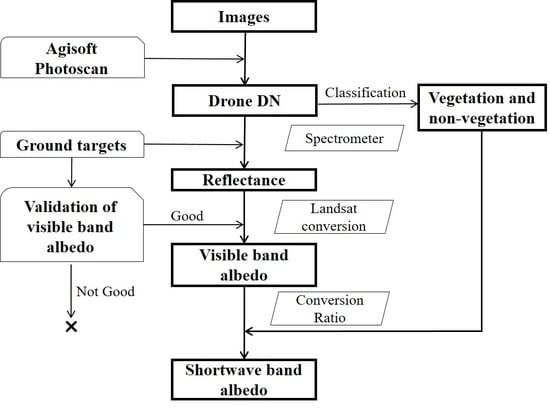
2. Materials and Methods
2.1. UAV Experiments
2.2. Image Processing
2.3. Spectrometer Measurement of Ground Targets
2.4. Landscape Albedo Estimation
2.5. Retrieval of Landscape Albedo from the Landsat Satellite
3. Results
3.1. Relationship Between the DN Values and Spectral Reflectance
3.2. Landscape Visible-Band and Shortwave Albedo
4. Validation
4.1. Validation of LANDSAT Visible Band Albedo Conversion Algorithm
4.2. Landscape Albedo Validation
5. Discussion
5.1. Effect of Sky Conditions on Albedo Estimation
5.2. Uncertainty in Landscape Shortwave Albedo
5.3. Potential Applications
6. Conclusions and Future Outlook
- (1)
- By adopting the method in this study, the landscape visible and shortwave band albedos of the Brooksvale Park were 0.086 and 0.332, respectively. For the Yale playground, the visible band albedo was 0.037, and shortwave albedo was between 0.054 and 0.061.
- (2)
- The Landsat satellite algorithm for converting the satellite spectral albedo to broadband albedo can also be used to convert spectral albedo that is acquired by drones to broadband albedo.
- (3)
- Data for spectral calibration using ground targets should be obtained under sky conditions that match those under which the drone flight take place. Because the relationship between the imagery DN value and the reflectivity is highly nonlinear, the ground targets should cover the range of reflectivity of the entire landscape.
- (4)
- In the current configuration, the drone estimate of the visible band albedo is more satisfactory than its estimate of shortwave albedo, when compared with the Landsat-derived values. We suggest that deployment of a camera with the additional capacity of measuring reflectance in a near-infrared waveband should improve the estimate of shortwave albedo. Future cameras with the capacity to detect mid-infrared reflectance will further improve the shortwave albedo detection. The BRDF effect, which was ignored in this study, should be taken into consideration when deciding the ground calibration targets and training data in future studies.
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Liang, S. Narrowband to broadband conversions of land surface albedo I: Algorithms. Remote Sens. Environ. 2001, 76, 213–238. [Google Scholar] [CrossRef]
- Hock, R. Glacier melt: A review of processes and their modelling. Prog. Phys. Geogr. 2005, 29, 362–391. [Google Scholar] [CrossRef]
- Jin, Y.; Schaaf, C.B.; Gao, F.; Li, X.; Strahler, A.H.; Zeng, X.; Dickinson, R.E. How does snow impact the albedo of vegetated land surfaces as analyzed with MODIS data? Geophys. Res. Lett. 2002, 29, 1374. [Google Scholar] [CrossRef]
- Myhre, G.; Kvalevåg, M.M.; Schaaf, C.B. Radiative forcing due to anthropogenic vegetation change based on MODIS surface albedo data. Geophys. Res. Lett. 2005, 32, L21410. [Google Scholar] [CrossRef]
- Jin, Y.; Randerson, J.T.; Goetz, S.J.; Beck, P.S.; Loranty, M.M.; Goulden, M.L. The influence of burn severity on postfire vegetation recovery and albedo change during early succession in North American boreal forests. J. Geophys. Res. Biogeosci. 2012, 117, G01036. [Google Scholar] [CrossRef]
- Cescatti, A.; Marcolla, B.; Vannan, S.K.; Pan, J.Y.; Román, M.O.; Yang, X.; Ciais, P.; Cook, R.B.; Law, B.E.; Matteucci, G.; et al. Intercomparison of MODIS albedo retrievals and in situ measurements across the global FLUXNET network. Remote Sens. Environ. 2012, 121, 323–334. [Google Scholar] [CrossRef] [Green Version]
- Fernández, T.; Pérez, J.L.; Cardenal, J.; Gómez, J.M.; Colomo, C.; Delgado, J. Analysis of landslide evolution affecting olive groves using UAV and photogrammetric techniques. Remote Sens. 2016, 8, 837. [Google Scholar] [CrossRef]
- Watts, A.C.; Ambrosia, V.G.; Hinkley, E.A. Unmanned aircraft systems in remote sensing and scientific research: Classification and consideration of use. Remote Sens. 2012, 4, 1671–1692. [Google Scholar] [CrossRef]
- Salamí, E.; Barrado, C.; Pastor, E. UAV flight experiments applied to the remote sensing of vegetated areas. Remote Sens. 2014, 6, 11051–11081. [Google Scholar] [CrossRef] [Green Version]
- Nex, F.; Remondino, F. UAV for 3D mapping applications: A review. Appl. Geomat. 2014, 6, 1–15. [Google Scholar] [CrossRef]
- Laliberte, A.S.; Goforth, M.A.; Steele, C.M.; Rango, A. Multispectral remote sensing from unmanned aircraft: Image processing workflows and applications for rangeland environments. Remote Sens. 2011, 3, 2529–2551. [Google Scholar] [CrossRef]
- Stolaroff, J.K.; Samaras, C.; O’Neill, E.R.; Lubers, A.; Mitchell, A.S.; Ceperley, D. Energy use and life cycle greenhouse gas emissions of drones for commercial package delivery. Nat. Commun. 2018, 9, 409. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Li, C.; Wang, Y.; Yuan, H.; Feng, H.; Xu, B.; Yang, X. The DOM generation and precise radiometric calibration of a UAV-mounted miniature snapshot hyperspectral imager. Remote Sens. 2017, 9, 642. [Google Scholar] [CrossRef]
- Sonnentag, O.; Hufkens, K.; Teshera-Sterne, C.; Young, A.M.; Friedl, M.; Braswell, B.H.; Milliman, T.; O’Keefe, J.; Richardson, A.D. Digital repeat photography for phenological research in forest ecosystems. Agric. For. Meteorol. 2012, 152, 159–177. [Google Scholar] [CrossRef]
- Saari, H.; Pellikka, I.; Pesonen, L.; Tuominen, S.; Heikkilä, J.; Holmlnd, C.; Mäkynen, J.; Ojala, K.; Antila, T. Unmanned Aerial Vehicle (UAV) operated spectral camera system for forest and agriculture applications. Proc. SPIE 2011, 8174, 466–471. [Google Scholar]
- Johnson, L.F.; Herwitz, S.; Dunagan, S.; Lobitz, B.; Sullivan, D.; Slye, R. Collection of ultra high spatial and spectral resolution image data over California vineyards with a small UAV. In Proceedings of the International Symposium on Remote Sensing of Environment, Beijing, China, 22–26 April 2003. [Google Scholar]
- Berni, J.A.J.; Suárez, L.; Fereres, E. Remote Sensing of Vegetation from UAV Platforms Using Lightweight Multispectral and Thermal Imaging Sensors. Available online: http://www.isprs.org/proceedings/XXXVIII/1_4_7-W5/paper/Jimenez_Berni-155.pdf (accessed on 21 March 2016).
- Zahawi, R.A.; Dandois, J.P.; Holl, K.D.; Nadwodny, D.; Reid, J.L.; Ellis, E.C. Using lightweight unmanned aerial vehicles to monitor tropical forest recovery. Biol. Conserv. 2015, 186, 287–295. [Google Scholar] [CrossRef] [Green Version]
- Bendig, J.; Yu, K.; Aasen, H.; Bolten, A.; Bennertz, S.; Broscheit, J.; Gnyp, M.L.; Bareth, G. Combining UAV-based plant height from crop surface models, visible, and near infrared vegetation indices for biomass monitoring in barley. Int. J. Appl. Earth Obs. 2015, 39, 79–87. [Google Scholar] [CrossRef]
- Levy, C.; Burakowski, E.; Richardson, A. Novel measurements of fine-scale albedo: Using a commercial quadcopter to measure radiation fluxes. Remote Sens. 2018, 10, 1303. [Google Scholar] [CrossRef]
- Hakala, T.; Suomalainen, J.; Peltoniemi, J.I. Acquisition of Bidirectional Reflectance Factor Dataset Using a Micro Unmanned Aerial Vehicle and a Consumer Camera. Remote Sens. 2010, 2, 819–832. [Google Scholar] [CrossRef] [Green Version]
- Ryan, J.; Hubbard, A.; Box, J.E.; Brough, S.; Cameron, K.; Cook, J.; Cooper, M.; Doyle, S.H.; Edwards, A.; Holt, T.; et al. Derivation of High Spatial Resolution Albedo from UAV Digital Imagery: Application over the Greenland Ice Sheet. Front. Earth Sci. 2017, 5. [Google Scholar] [CrossRef] [Green Version]
- Lebourgeois, V.; Bégué, A.; Labbé, S.; Mallavan, L.; Prévost, B.R. Can Commercial Digital Cameras Be Used as Multispectral Sensors? A Crop Monitoring Test. Sensors 2008, 8, 7300–7322. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lelong, C.C.D.; Burger, P.; Jubelin, G.; Roux, B.; Labbé, S.; Baret, F. Assessment of Unmanned Aerial Vehicles Imagery for Quantitative Monitoring of Wheat Crop in Small Plots. Sensors 2008, 8, 3557–3585. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Markelin, L.; Honkavaara, E.; Peltoniemi, J.; Ahokas, E.; Kuittinen, R.; Hyyppä, J.; Suomalainen, J.; Kukko, A. Radiometric Calibration and Characterization of Large-format Digital Photogrammetric Sensors in a Test Field. Photogramm. Eng. Remote Sens. 2008, 74, 1487–1500. [Google Scholar] [CrossRef]
- Honkavaara, E.; Arbiol, R.; Markelin, L.; Martinez, L.; Cramer, M.; Bovet, S.; Chandelier, L.; Ilves, R.; Klonus, S.; Marshal, P.; et al. Digital Airborne Photogrammetry—A New Tool for quantitative remote sensing? A State-of-Art review on Radiometric Aspects of Digital Photogrammetric Images. Remote Sens. 2009, 1, 577–605. [Google Scholar] [CrossRef] [Green Version]
- Du, M.; Noguchi, N. Monitoring of Wheat Growth Status and Mapping of Wheat Yield’s within-Field Spatial Variations Using Color Images Acquired from UAV-camera System. Remote Sens. 2017, 9, 289. [Google Scholar] [CrossRef]
- Wang, M.; Chen, C.; Pan, J.; Zhu, Y.; Chang, X. A Relative Radiometric Calibration Method Based on the Histogram of Side-Slither Data for High-Resolution Optical Satellite Imagery. Remote Sens. 2018, 10, 381. [Google Scholar] [CrossRef]
- Shuai, Y.; Masek, J.; Gao, F.; Schaaf, C. An algorithm for the retrieval of 30-m snow-free albedo from Landsat surface reflectance and MODIS BRDF. Remote Sens. Environ. 2011, 115, 2204–2216. [Google Scholar] [CrossRef]
- Wang, Z.; Erb, A.M.; Schaaf, C.B.; Sun, Q.; Liu, Y.; Yang, Y.; Shuai, Y.; Casey, K.A.; Roman, M.O. Early spring post-fire snow albedo dynamics in high latitude boreal forests using Landsat-8 OLI data. Remote Sens. Environ. 2016, 185, 71–83. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Available online: http://www.cielmap.com/cielmap/ (accessed on 28 June 2016).
- Agisoft Photoscan User Manual. Available online: http://www.agisoft.com/pdf/photoscan-pro_1_2_en.pdf/ (accessed on 18 July 2016).
- Kruse, F.A.; Lefkoff, A.B.; Boardman, J.W.; Heidebrecht, K.B.; Shapiro, A.T.; Barloon, P.J.; Goetz, A.F.H. The spectral image processing system (SIPS)—Interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Gueymard, C.A. The sun’s total and spectral irradiance for solar energy applications and solar radiation models. Sol. Energy 2004, 76, 423–453. [Google Scholar] [CrossRef]
- He, T.; Liang, S.; Wang, D.; Cao, Y.; Gao, F.; Yu, Y.; Feng, M. Evaluating land surface albedo estimation from Landsat MSS, TM, ETM+, and OLI data based on the unified direct estimation approach. Remote Sens. Environ. 2018, 204, 181–196. [Google Scholar] [CrossRef]
- Landsat8 Surface Reflectance Code (LaSRC) Product Guide. Available online: https://landsat.usgs.gov/sites/default/files/documents/lasrc_product_guide.pdf (accessed on 14 February 2018).
- Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
- Payne, R.E. Albedo of the sea surface. J. Atmos. Sci. 1972, 29, 959–970. [Google Scholar] [CrossRef]
- Brest, C.; Goward, S. Deriving surface albedo measurements from narrow band satellite data. Int. J. Remote Sens. 1987, 8, 351–367. [Google Scholar] [CrossRef]
- Brest, C. Seasonal albedo of an urban/rural landscape from satellite observations. J. Clim. Appl. Meteorol. 1987, 26, 1169–1187. [Google Scholar] [CrossRef]
- Zhao, L.; Lee, X.; Schultz, M. A wedge strategy for mitigation of urban warming in future climate scenarios. Atmos. Chem. Phys. 2017, 17, 9067–9080. [Google Scholar] [CrossRef] [Green Version]
- Akbari, H.; Kolokotsa, D. Three decades of urban heat islands and mitigation technologies research. Energy Build. 2016, 133, 834–842. [Google Scholar] [CrossRef]






| Brooksvale Recreation Park | Yale Playground | |
|---|---|---|
| Location | 41.453°N 72.918°W | 41.317°N 72.928°W |
| Drone experiment date | 9 October 2015 | 30 September 2015 |
| Drone flight time | 10:00 to 10:30 | 14:30 to 15:00 |
| Sky conditions | Overcast | Clear sky |
| Flight duration | 30 min | 20 min |
| Flight altitude (m) | 120 | 90 |
| Camera | Sony NEX-5N | GARMIN VIRB-X |
| UAV platform | Fixed-wing | Quad-rotor |
| Forward overlap | 80% | 80% |
| Side overlap | 60% | 60% |
| Image overlap Area (km2) | >9 0.065 | >9 0.014 |
| Sky Conditions | Brooksvale Park | Yale Playground |
|---|---|---|
| Clear | 28 April 2016 10:00 | 19 April 2016 14:30 |
| Overcast | 7 March 2016 10:00 | 28 April 2016 14:30 |
| Brooksvale Park | Yale Playground | |
|---|---|---|
| Drone-derived visible band albedo | c: 0.077 ± 0.091 | c: 0.037 ± 0.063 |
| o: 0.086 ± 0.110 | o: 0.054 ± 0.090 | |
| Landsat 8 visible band albedo | 0.054 ± 0.011 | 0.047 ± 0.012 |
| Drone-derived shortwave band albedo | c: 0.261 ± 0.395 | SN: 0.054 ± 0.074 |
| o: 0.332 ± 0.527 | SV: 0.061 ± 0.076 | |
| Landsat 8 shortwave band albedo | 0.103 ± 0.019 | 0.128 ± 0.013 |
| Sky Condition | Brooksvale Park | Yale Playground | ||
|---|---|---|---|---|
| Vegetation | Non-Vegetation | Vegetation | Non-Vegetation | |
| Clear | 5.08 | 1.18 | 3.91 | 1.24 |
| Overcast | 6.76 | 1.20 | 5.29 | 1.18 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, C.; Lee, X.; Muhlhausen, J.; Bonneau, L.; Xu, J. Measuring Landscape Albedo Using Unmanned Aerial Vehicles. Remote Sens. 2018, 10, 1812. https://doi.org/10.3390/rs10111812
Cao C, Lee X, Muhlhausen J, Bonneau L, Xu J. Measuring Landscape Albedo Using Unmanned Aerial Vehicles. Remote Sensing. 2018; 10(11):1812. https://doi.org/10.3390/rs10111812
Chicago/Turabian StyleCao, Chang, Xuhui Lee, Joseph Muhlhausen, Laurent Bonneau, and Jiaping Xu. 2018. "Measuring Landscape Albedo Using Unmanned Aerial Vehicles" Remote Sensing 10, no. 11: 1812. https://doi.org/10.3390/rs10111812
APA StyleCao, C., Lee, X., Muhlhausen, J., Bonneau, L., & Xu, J. (2018). Measuring Landscape Albedo Using Unmanned Aerial Vehicles. Remote Sensing, 10(11), 1812. https://doi.org/10.3390/rs10111812