1. Introduction
Urban green cover can be defined as the layer of leaves, branches, and stems of trees and shrubs and the leaves of grasses that cover the urban ground when viewed from above [
1]. This term is typically used to refer to urban green space identified from remote sensing data, as it is in this study. Green space is an essential infrastructure in cities because it provides various products and ecosystem services for urban dwellers that can address support to climate-change mitigation and adaptation, human health and well-being, biodiversity conservation, and disaster risk reduction [
2]. Therefore, inventorying the spatial distribution of urban green cover is imperative in decision-making about urban management and planning [
3].
High-spatial resolution (HR) remote sensing data have shown great potential in identifying both the extent and the corresponding attributes of urban green cover [
4,
5,
6,
7,
8]. In order to fully exploit the information content of the HR images, geographic object-based image analysis (GEOBIA) has become the principal method [
9] and has been successfully applied for urban green cover extraction [
10,
11,
12,
13,
14,
15]. Scale is a crucial aspect in GEOBIA as it describes the magnitude or the level of aggregation and abstraction on which a certain phenomenon can be described [
16]. GEOBIA is sensitive to segmentation scale but has challenges in selecting scale parameters, because different objects can only be perfectly expressed at the scale corresponding to their own granularity. The urban green cover in HR images presents obvious multiscale characteristics, for example, the size of urban green cover varies in a large extent of scales; it can either be a small area with several square meters, such as a private garden, or reach a large area with several square kilometers such as a park. As a result, it is be possible to properly segment all features in a scene using a single segmentation scale, resulting in that over-segmentation (producing too many segments) or under-segmentation (producing too few segments) often occurs [
17]. Therefore, it plays a decisive role in GEOBIA that divide the complex features at the appropriate scale to segment landscape into non-overlapping homogenous regions [
18].
In order to find the optimal scale for each object, the multiscale segmentation can be optimized using three different strategies based on: supervised evaluation measures, unsupervised evaluation measures, and cross-scale optimization. (1) The supervised strategy compares segmentation results with reference by geometric [
19,
20,
21,
22,
23] and arithmetic [
21,
24,
25] discrepancy. This strategy is apparently effective but is, in fact, subjective and time-consuming when creating the reference. (2) The unsupervised strategy defines quality measures, such as intra-region spectral homogeneity [
26,
27,
28,
29,
30,
31] and inter-region spectral heterogeneity [
32,
33,
34], for conditions to be satisfied by an ideal segmentation. It thus characterizes segmentation algorithms by computing goodness measures based on segmentation results without the reference. This strategy is objective but has the added difficulty of designing effective measures. (3) The cross-scale strategy fuses multiscale segmentations to achieve the expression of various granularity of objects at their optimal scale [
35,
36,
37]. It can make better use of the multiscale information than the other two strategies.
Recently, cross-scale strategy has garnered much attention in the multiscale segmentation optimization by using evaluation measures as the indicator. (1) For the unsupervised indicator, some studies generated a single optimal segmentation by fusing multiscale segmentations according to local-oriented unsupervised evaluation [
35,
38,
39]. However, the range of involved scales was found to be limited. By contrast, multiple segmentation scales were selected according to a change in homogeneity [
27,
28,
29]. (2) For the supervised indicator, multiscale segmentation optimization has been achieved by using the single-scale evaluation measure based on different sets of reference objects [
28]. For example, some studies have provided reference objects and suitable segmentation scales for different land cover types [
40,
41]. The difficulty of this strategy is preparing appropriate sets of reference objects that can reflect changes of scales. In our previous work [
37], two discrepancy measures are proposed to assess multiscale segmentation accuracy: the multiscale object accuracy (MOA) measure at object level and the bidirectional consistency accuracy (BCA) measure at pixel level. The evaluation results show that the proposed measures can assess multiscale segmentation accuracy and indicate the manner in which multiple segmentation scales can be selected. These proposed measures can manage various combinations of multiple segmentation scales. Therefore, applications for optimization of multiscale segmentation can be expanded.
In this study, an unsupervised cross-scale optimization method specifically for urban green cover segmentation is proposed. A global optimal segmentation is first selected from multiscale segmentation results by using an optimization indicator. The regions in the global optimal segmentation are then isolated into under- and fine-segmentation parts. The under-segmentation regions are further locally refined by using the same indicator as that in global optimization. Finally, the fine-segmentation part and the refined under-segmented part are combined to obtain the final cross-scale optimization result. The goal of the proposed method is to segment urban vegetation in general, for example, trees and grass together included in one region. The segmentation result of urban green cover can be practically used in urban planning, for example investigation of urban green cover rate [
42,
43], and urban environment monitoring, for example influence analysis of the urban green cover to residential quality [
44,
45].
The contribution of this study is to propose a new cross-scale optimization method specifically for urban green cover to achieve the optimal segmentation scale for each green cover object. The same optimization indicator is designed to be used both to identify the global optimal scale and to refine the under-segmentation. By refining the isolated under-segmented regions for urban green cover, the optimization result can avoid under-segmentation errors as well as reduce over-segmentation errors, achieving higher segmentation accuracies than single-scale segmentation results. The proposed method also holds the potentials to be applied to cross-scale segmentation optimization for different types of urban green cover or even other land cover types by designing proper under-segmentation isolation rule.
The rest of the paper is organized as follows.
Section 2 presents the proposed method of multiscale segmentation optimization.
Section 3 describes the study area and test data.
Section 4 verifies the effectiveness of the proposed method based on experiments.
Section 5 presents the discussions. Finally, conclusions are drawn in
Section 6.
2. Method
2.1. General Framework
This study proposes a multiscale optimization method for urban green cover segmentation, which aims to comprehensively utilize multiscale segmentation results to achieve optimal scale expression of urban green cover.
Figure 1 shows the general framework of the proposed method. First, a global optimal segmentation is selected from the multiscale segmentation results by using an optimization indicator. The indicator is the local peak (
LP) of the change rate (
CR) of the mean value of spectral standard deviation (
SD) of each segment. Second, the regions in the global optimal segmentation result are isolated into under- and fine-segmentation parts, based on designed under-segmentation isolation rule. Third, the under-segmentation regions are refined by using the same optimization indicator
LP in a local version. Finally, the fine-segmented part and the optimized under-segmented part are combined to obtain the final cross-scale optimization result.
2.2. Hierarchical Multiscale Segmentation
The hierarchical multiscale segmentation is composed of multiple segments from fine to coarse at each location, in which the small objects are supposed to be represented by fine segments at certain segmentation scales and the large objects are represented by coarse segments correspondingly. Furthermore, a fine-scale segment smaller than a real object is supposed to represent a part of the object, while a coarse-scale segment larger than a real object is to represent an object group. A preliminary requirement for the multiscale segments is that the segments at the same location should be nested. Otherwise the object boundaries would be conflict when combining or fusing the multiscale segments.
The hierarchical multiscale segmentation is represented using a segment tree model [
46], as shown in
Figure 2. The tree nodes at different levels represent segments at different scales. An arc connecting a parent and a child node represents the inclusion relation between segments at adjacent scales. The leaf nodes represent the segments at the finest scale and the nodes at upper levels represent segments at coarser scales. Finally, the root node represents the whole image. An ancestry path in the tree is defined as the path from a leaf node up to the root node, revealing the transition from object part to the whole scene. The hierarchical context of each leaf node is conveyed by the ancestry path, in which a segment is gradually becoming coarser and finally reaching the whole image.
Several region-based segmentation methods can be applied to produce the required hierarchical multiscale segmentations, for example multiresolution segmentation method [
47], mean-shift method [
48] and hierarchical method [
49]. Specifically, the multiresolution segmentation method [
47] is used in the study, in which the shape parameter is set as 0.5 by default. The regions at each segmentation scale are represented by the nodes at the same level in the segment tree. Finally, the segment tree is constructed by recording the multiscale segmentation.
2.3. Selecting Global Optimal Scale
We need to first select a global optimal segmentation scale and then refine the under-segmentation part for urban green cover. Thus, unlike other optimal scale selection methods for compromising under- and over-segmentation errors, we design an indicator to select an optimal scale in which segmentation results mainly include reasonable under-segmented and fine-segmented regions, reducing over-segmented regions as much as possible.
Referring to the standard deviation indicator [
28], we adopt the indicator focusing on homogeneity of segments by calculating the mean value of spectral standard deviation (
SD) of each segment.
SD is defined as below:
where
SDki is the standard deviation of digital number (DN) of spectral band
k in segment
i;
n is the number of segments in the image; and
b is the number of spectral bands of the image.
With the increase of the scale parameter,
SD will change as following. Generally, it tends to increase because the homogeneity of segments is gradually decreased in the region merging procedure. Near the scale that the segments are close to the real objects, the change rate of
SD will increase suddenly because of the influence of the boundary pixels [
29].
To find the scale in which the green cover segments are closest to the real objects, we propose indicator
CR to represent the change rate of
SD and indicator
LP to represent the local peak of
CR. They are defined respectively as below:
where
l is the segmentation scale and Δ
l is the increment in scale parameter, that is the lag at which the scale parameter grows. The scale increment has powerful control over the global optimal segmentation because it can smooth the heterogeneity measure resulting in the optimal segmentation occurred in different scales [
50]. Experimentally, the small increments (e.g., 1) produces optimal segmentation in finer scales while the large increments (e.g., 100) produces optimal segmentation in coarser scales [
28]. Hence, the medium increment (e.g., 10) of scale is adopted in the study.
According to the aforementioned change law of SD, near the scale that the segments are close to the real objects, the CR will increase suddenly because of the influence of the boundary pixels of green cover segments. Thus, a LP will appear when the global optimal segmentation scale is coming for several segments. However, there are several LPs within a set of increased scale parameters because not all the segments have the same optimal segmentation scale. The global optimal segmentation is identified as the scale with largest LP, because the largest LP indicates that most of the segments in the image reach the optimal segmentation state. Furthermore, the large LP could also be caused by the large SD value of coarse segments, because the large SD will produce large CR and corresponding large LP, revealing the under-segmentation state. Therefore, the next step is to optimize the under-segmentation part of the global optimal segmentation result for green cover objects.
2.4. Isolating Under-Segmented Regions
In order to obtain the under-segmented regions for green cover from the globally optimized segmentation result, further isolation of segments is required. When a green cover object is in the under-segmentation state, it is often mixed with other adjacent objects and the spectral standard deviation (
SDi) is thus great. Moreover, since the normalized difference vegetation index (NDVI) has a good performance to distinguish between green cover and other features, when other objects are mixed with the green cover object, the NDVI value of the region is not very high, that is lower than that of green cover objects, as well as not very low, that is higher than that of non-green cover objects. NDVI is defined as the ratio of difference between near infrared band and red band values to their sum [
51]. Thus, NDVI of a region is calculated as below:
where
NIRj and
Rj are DNs of near infrared and red band for pixel
j, respectively; and
m is the number of pixels in region
i.
Therefore, a region with a high
SDi value and a medium
NDVIi value can be considered an under-segmentation region for green cover. The isolation rule for an under-segmentation region with green cover are thus defined as below:
where
TSD,
TN1, and
TN2 are thresholds that need to be set by users. We set it by the trial-and-error strategy. A segment with
SDi lower than
TSD is viewed as fine segment because of the high homogeneity. If the
NDVIi value of region
i is higher than
TN2, it is viewed as fine segmentation of green cover; and if it is lower than
TN1, it is viewed as not containing green cover and will not be involved in the successive refining procedure.
2.5. Refining Under-Segmented Regions
For each individual region in the under-segmentation part, the segment tree is first used to quantify the spatial context relationship of the regions at different scales and the appropriate segmentation scale is then selected through the optimization indicator LP. Finally, the under-segmentation part is replaced by the optimized segments. The specific steps are performed as follows:
- (1)
Select one under-segmented region Ri, extract the segmentations at lower scales than the global optimal scale in region Ri.
- (2)
Compute the LP of each scale and the local optimal scale of green cover is defined as scale with a largest LP in region Ri.
- (3)
Replace Ri with the local optimal scale segmentation.
- (4)
Repeat step (1)–(3) until all under-segmented regions are refined according to Equation (5).
2.6. Accuracy Assessment
Segmentation quality evaluation strategies include visual analysis, system-level evaluation, empirical goodness, and empirical discrepancy methods [
37]. The last two methods are also known as unsupervised and supervised evaluation methods, respectively. The unsupervised evaluation method calculates indexes of homogeneity within segments and heterogeneity between segments [
35]. It does not require ground truth but the explanatory of designing measures and the meaning of measure values is insufficient. The supervised evaluation method compares segmentation results with ground truth and its discrepancy can directly reveal the segmentation quality [
52]. Region-based
precision and
recall measures are sensitive to both geometric and arithmetic errors. Thus, the supervised evaluation method is used to assess the segmentation accuracy of the multiscale optimization.
Precision is the ratio of true positives to the sum of true positives and false positives, and
recall is the ratio of true positives to the sum of true positives and false negatives. Given the segmentation result
S with
n segments {
S1,
S2, …,
Sn} and the reference
R with
m objects {
R1,
R2, …,
Rm}, the
precision measure is calculated by matching {
Ri} to each segment
Si and the
recall measure by matching {
Si} to each reference object
Ri. When calculating the
precision measure, the matched reference object (
Rimax) for each segment
Si is first identified, where
Rimax has the largest overlapping area with
Si. The
precision measure is then defined as [
23]:
where |
| denotes the area that is represented by the number of pixels in a region.
Similarly, the matched segment (
Simax) for each reference object
Ri is searched according to the maximal overlapping area criterion and the
recall measure is defined as [
23]:
The
precision and
recall measures both range from 0 to 1. Using these two measures can determine both under- and over-segmented situations. An under-segmented result will have a large
recall and a low
precision. By contrast, if the result is over-segmented, the
precision is high but the
recall is low. If the
precision and
recall values of one segmentation result are both higher than another, this result is considered to have a better segmentation quality. However, we do not know which one is better when one measure in larger than another and the other measure is smaller than another. Hence, we should combine these two measures into one. In this study, we use the harmonic average of
precision and
recall called
F-score [
53], which is defined as:
where an
F-score reaches its best value at 1 (perfect
precision and
recall) and worst at 0.
3. Data
The study area is located in Nanjing City (32°02′38″N, 118°46′43″E), which is the capital of Jiangsu Province of China and the second largest city in the East China region (
Figure 3), with an administrative area of 6587 km
2 and a total population of 8335 thousand as of 2017. As one of the four garden cities in China, Nanjing has a wealth of urban green spaces than many of other cities. The urban green cover rate in the built-up area of Nanjing is 44.85% in 2018.
In this study, an IKONOS-2 image acquired on 19 October 2010 and a WorldView-2 image acquired on 29 July 2015 in Nanjing are used as the HR data. Both the images consist of four spectral bands: blue, green, red, and near infrared. The spatial resolution of the multispectral bands of the IKONOS-2 image is improved from 3.2 m to 0.8 m after pan-sharpening. The spatial resolution of the multispectral bands of the WorldView-2 image is 2 m.
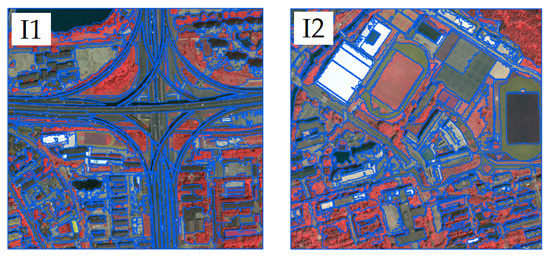
Two test images identified as I1 and I2 are subsets of the IKONOS-2 and the WorldView-2 images, respectively, containing urban green cover in traffic area, residential area, campus area, park area, commercial area, and industrial area, which are the typical areas in urban. The size of I1 and I2 are 2286 × 1880 and 1478 × 974 pixels and the area are approximate 2.8 km
2 and 5.8 km
2, respectively. As shown in
Figure 4, there are abundant green cover objects distributed in the images and various in size and shape.
In order to evaluate the segmentation accuracy, we randomly select some green cover objects as reference. The reference objects are uniformly distributed in the test images and various in size and shape. Each reference object is delineated by one person and reviewed by other to catch any obvious errors. Finally, we collect 130 reference objects for each test image. It is noted that if there are trees covered a road, this area will be digitized as green cover objects. The area of the smallest reference object is only 59.5 m2, whereas the area of the biggest reference object is 14,063.1 m2. Hence, it is not possible to properly segment all of the green cover objects using a single segmentation scale.
4. Results
4.1. Global Optimal Scale Selection
The multiscale segmentation results are produced by applying multiresolution segmentation method. For I1, the scale parameters are set from 10 to 250 by increment of 10. Since the spatial resolution of I2 is coarser than I1, the scale parameters are set from 10 to 125 by increment of 5. If we set the same scale parameters for I2 as those for I1, the coarse segmentation scales (e.g., >130) would be seriously under-segmented and the homogeneity of segments at these coarse scales would change randomly, which could not benefit the optimization procedure and could even do harm to the optimization procedure.
The multiscale segmentations cover apparently over-segmentation, medium segmentation, and apparently under-segmentation. The optimization indicators
SD,
CR, and
LP are respectively calculated for each segmentation result and shown in
Figure 5. When the scale parameter increases,
SD gradually increases, which indicates that the regions are gradually growing and the homogeneity decreases. Correspondingly, in the process of
SD change,
CR appears multiple local peaks. The indicator
LP can highlight these local peaks of
CR very well. We can see that
LP appears at segmentation scales of 80, 110, 150, 170, 190, and 220 for I1, in which
LP reaches the maximum at 220. For I2,
LP appears at segmentation scales of 45, 55, 60, 70, 80, 85, 95, 105, and 120, where
LP is the largest at 105. Therefore, the segmentation with the scale parameter of 220 and 105 is taken as the global optimal segmentation scale for I1 and I2.
Combining with the supervised evaluation results of the multiscale segmentations (
Figure 6), we can know that the selected global optimal segmentation scale is at the under-segmentation status for green cover objects. For both I1 and I2, the
precision value is apparently lower than the
recall value in the optimal scale, which indicates the under-segmentation status. To further illustrate this, the selected I2 segmentation result at scale 105 is presented in
Figure 7, in which we can clearly see that except for several fine-segmented green cover objects with relatively large size, many green cover objects are shown as under-segmented.
The selected global optimal segmentation of green cover tends to appear in the case of coarse scales. As a result, the over-segmentation errors are reduced, while some green cover objects with small size will inevitably be in an under-segmentation state and single scale cannot achieve optimal segmentation of green cover objects of different sizes. Therefore, it is necessary to further optimize the global optimal segmentation by refining the under-segmented regions.
4.2. Under-Segmented Region Isolation
The under-segmented regions are isolated by the rule in Equation (5). The threshold values of TSD, TN1, and TN2 are set as 40, 0.05, and 0.25 for test image I1 and as 40, 0.10, and 0.55 for test image I2. The threshold values of NDVIi for I2 is set as different for I1, this is mainly because the different acquisition date between I1 and I2, between which the vegetation growth status is different.
To illustrate the effectiveness of the designed isolation rule for under-segmentation with green cover, several sample segments in the global optimal segmentations are presented in
Figure 8. It can be seen that the under-segmented regions containing green cover have medium
NDVIi values and high
SDi values, as shown in
Figure 8a,b,f,g. The fine-segmentation of green cover present high
NDVIi values as shown in
Figure 8c,i. A special case of fine-segmentation is shown in
Figure 8h, which is a segment mainly containing sparse grass and the
NDVIi value is thus not very high. However, the relatively low
SDi value of grass segment can prevent it to be wrongly identified as under-segmentation. The segments without green cover usually present low
NDVIi value as shown in
Figure 8d. A special case of segment without green cover is shown in
Figure 8e, where the roof segment has a medium
NDVIi value because of the roof material. However, the relatively low
SDi value can prevent it to be wrongly identified as under-segmentation containing green cover.
To further validate the effectiveness of the isolation rule, the up-left part of the isolation results of I1 and I2 is zoomed in
Figure 9. It can be seen that the green cover and other objects are mixed in the isolated under-segmented regions. In the fine-segmentation part, the regions are either fine-segmented green cover or segments without green cover.
4.3. Under-Segmented Region Refinement
The multiscale optimized segmentation is obtained by refining the under-segmented part of the global optimal scale. In the refinement segmentation result, with the benefit of cross-scale refinement strategy, the segments are at different segmentation scales to achieve the optimal segmentation scale for each green cover object. The histogram of segmentation scales in the refinement results is shown in
Figure 10. The refined segments almost cover all the segmentation scales finer than the selected global optimal scale. There are many segments at the small segmentation scales, for example scale 20 to 40 for I1 and scale 15 to 25 for I2, because there are many small-size green cover objects in urban area, such as single trees.
To illustrate the effectiveness of achieving optimal scale for each green cover object, the sample refinement results from test images are enlarged to present in
Figure 11 with labels of the scale number for each segment. Generally, it can be seen that large green cover objects are segmented at relatively coarse segmentation scales while small green cover objects are segmented at relatively small segmentation scales. The green cover objects, especially the small ones, tend to be segmented by a single segment.
The supervised evaluation results of segmentation before and after refinement are presented in
Table 1 to quantify the effectiveness of the under-segmentation refinement. It can be seen that the
precision value is apparently improved after refinement, showing that the under-segmented green cover objects can be effectively refined. The
recall value is decreased mainly because the reduced under-segmentation. Therefore, the
F-score after refinement is apparent improved than that before refinement. The segmentation results before and after refinement shown in
Figure 12 further prove this.
To quantify the effectiveness of cross-scale optimization, the refinement result is compared with single-scale segmentation that has the highest
F-score in the produced multiscale segmentations, which is at scale 70 for I1 and 35 for I2. The supervised evaluation results are also presented in
Table 1. It can be seen that the
precision of the refinement result is slightly lower than that of the single-scale best result while the
recall is higher, which could be caused by the over-segmentation of the large green cover objects. Another reason for the lower
precision for the refinement result could be caused by the wrong identification of under-segmented green cover objects, which makes the under-segmentation cannot be refined and thus lowers the precision accuracy. As a whole, the
F-score of the refinement result is slightly higher than that of the single-scale best segmentation, which could mainly be caused by the reduced under-segmentation errors in the refining procedure. The segmentation results presented in
Figure 11 further show the difference. As highlighted by the yellow rectangles, the existed under-segmentation errors in the single-scale best segmentation can be effectively reduced by the proposed refining strategy, which indicates the effectiveness of the refining procedure on overcoming under-segmentation errors. According to the comparison result with single-scale best segmentation, we can safely conclude that the proposed unsupervised multiscale optimization method can automatically produce optimal segmentation result at least equals to single-scale best segmentation indicated by supervised evaluation. Furthermore, the proposed refining strategy can help to reduce under-segmentation errors even in the single-scale best segmentation.
6. Conclusions
In this paper, a multiscale optimized segmentation method for urban green cover is proposed. The global optimal segmentation result is first selected from the hierarchical multiscale segmentation results by using the optimization indicator global LP. Based on this, under-segmented regions and fine-segmented regions are isolated by the designed rule. For under-segmented regions, local LP is used for refinement, which ultimately allows urban green cover objects of different sizes to be expressed at their optimal scale.
The effectiveness of proposed cross-scale optimization method is proved by experiments based on two test HR images in Nanjing, China. With the benefit of cross-scale optimization, the proposed unsupervised multiscale optimization method can automatically produce optimal segmentation result with higher segmentation accuracy than single-scale best segmentation indicated by supervised evaluation. Furthermore, the proposed refining strategy is demonstrated to be able to effectively reduce under-segmentation errors.
The proposed method can be improved and extended in the future, for example optimizing segmentation for different types of urban green cover or even other land cover types. The key step is to design appropriate isolation rule of under-segmentation for specific applications. To further explore the potentials of the proposed method would be the main future work based on this study.