Hierarchical Regularization of Building Boundaries in Noisy Aerial Laser Scanning and Photogrammetric Point Clouds
Abstract
:1. Introduction
2. Related Work
3. Hierarchical Regularization of Building Boundaries from Noisy Point Clouds
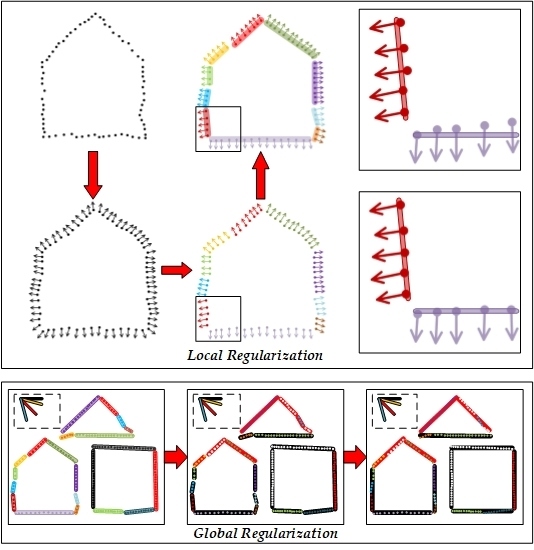
3.1. Overview of the Approach
3.2. Shiftable Line Fitting for Local Regularization
3.2.1. Outlier-Free Neighborhood Estimation
3.2.2. Robust Normal Estimation of Boundaries
3.2.3. Line Fitting with Shiftable Points
3.3. Constrained Model Selection for Global Regularization
3.3.1 Constrained Model Extension
3.3.2 Model Selection Using Graph Cut
4. Experimental Evaluation
4.1. Description of the Test Data and Evaluation Methods
4.2. Experimental Comparison of the Photogrammetric Point Clouds
4.3. Experimental Comparison of ALS Point Clouds
5. Discussions
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vosselman, G.; Maas, H. Airborne and Terrestrial Laser Scanning; Whittles Publishing: Caithness, UK, 2010; p. 336. [Google Scholar]
- Berger, M.; Tagliasacchi, A.; Seversky, L.; Alliez, P.; Levine, J.; Sharf, A.; Silva, C. State of the art in surface reconstruction from point clouds. In EUROGRAPHICS Star Reports; The Eurographics Association: Geneve, Switzerland, 2014; pp. 161–185. [Google Scholar]
- Moulon, P.; Monasse, P.; Marlet, R. Global fusion of relative motions for robust, accurate and scalable structure from motion. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013; pp. 3248–3255. [Google Scholar]
- Vu, H.; Labatut, P.; Pons, J.; Keriven, R. High accuracy and visibility-consistent dense multiview stereo. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 889–901. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Zhu, Q.; Du, Z.; Zhang, Y.; Ding, Y. Reliable spatial relationship constrained feature point matching of oblique aerial images. Photogramm. Eng. Remote Sens. 2015, 81, 49–58. [Google Scholar] [CrossRef]
- Rupnik, E.; Nex, F.; Toschi, I.; Remondino, F. Aerial multi-camera systems: Accuracy and block triangulation issues. ISPRS J. Photogramm. Remote Sens. 2015, 101, 233–246. [Google Scholar] [CrossRef]
- Xie, L.; Hu, H.; Wang, J.; Zhu, Q.; Chen, M. An asymmetric re-weighting method for the precision combined bundle adjustment of aerial oblique images. ISPRS J. Photogramm. Remote Sens. 2016, 117, 92–107. [Google Scholar] [CrossRef]
- Hirschmuller, H. Stereo processing by semiglobal matching and mutual information. IEEE Trans. Pattern Anal. Mach. Intell. 2008, 30, 328–341. [Google Scholar] [CrossRef] [PubMed]
- Hu, H.; Chen, C.; Wu, B.; Yang, X.; Zhu, Q.; Ding, Y. Texture-aware dense image matching using ternary census transform. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2016, 3, 59–66. [Google Scholar] [CrossRef]
- Zlatanova, S.; Rahman, A.A.; Shi, W. Topological models and frameworks for 3D spatial objects. Comput. Geosci. 2004, 30, 419–428. [Google Scholar] [CrossRef] [Green Version]
- Biljecki, F.; Ledoux, H.; Stoter, J. An improved LOD specification for 3D building models. Comput. Environ. Urban Syst. 2016, 59, 25–37. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.P.; Jain, K.; Mandla, V.R. Virtual 3D city modeling: Techniques and applications. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2013, 2, 73–91. [Google Scholar] [CrossRef]
- Biljecki, F.; Stoter, J.; Ledoux, H.; Zlatanova, S.; Çöltekin, A. Applications of 3D City Models: State of the Art Review. ISPRS Int. J. Geo-Inf. 2015, 4, 2842–2889. [Google Scholar] [CrossRef] [Green Version]
- Poux, F.; Neuville, R.; Nys, G.; Billen, R. 3D Point Cloud Semantic Modelling: Integrated Framework for Indoor Spaces and Furniture. Remote Sens. 2018, 10, 1412. [Google Scholar] [CrossRef]
- Bosche, F.; Haas, C.T.; Akinci, B. Automated recognition of 3D CAD objects in site laser scans for project 3D status visualization and performance control. J. Comput. Civ. Eng. 2009, 23, 311–318. [Google Scholar] [CrossRef]
- Lafarge, F.; Mallet, C. Creating large-scale city models from 3D-point clouds: A Robust Approach with Hybrid Representation. Int. J. Comput. Vis. 2012, 99, 69–85. [Google Scholar] [CrossRef]
- Albers, B.; Kada, M.; Wichmann, A. Automatic extraction and regularization of building outlines from airborne LIDAR point clouds. In Proceedings of the 2016 XXIII ISPRS Congress, Prague, Czech Republic, 12–19 July 2016. [Google Scholar]
- Cabral, R.; Furukawa, Y. Piecewise planar and compact floorplan reconstruction from images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Columbus, OH, USA, 23–28 June 2014; pp. 628–635. [Google Scholar]
- Lee, J.; Han, S.; Byun, Y.; Kim, Y. Extraction and regularization of various building boundaries with complex shapes utilizing distribution characteristics of airborne LIDAR points. ETRI J. 2011, 33, 547–557. [Google Scholar] [CrossRef]
- Xie, L.; Hu, H.; Zhu, Q.; Wu, B.; Zhang, Y. Hierarchical regularization of polygons for photogrammetric point clouds of oblique images. ISPRS-Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 42, 35–40. [Google Scholar] [CrossRef]
- Li, Z.; Openshaw, S. Algorithms for automated line generalization1 based on a natural principle of objective generalization. Int. J. Geogr. Inf. Syst. 1992, 6, 373–389. [Google Scholar] [CrossRef]
- Garrido, A.; Garcia-Silvente, M. Boundary simplification using a multiscale dominant-point detection algorithm. Pattern Recog. 1998, 31, 791–804. [Google Scholar] [CrossRef]
- Sester, M. Optimization approaches for generalization and data abstraction. Int. J. Geogr. Inf. Sci. 2005, 19, 871–897. [Google Scholar] [CrossRef]
- Xie, J.; Feng, C. An integrated simplification approach for 3D buildings with sloped and flat roofs. ISPRS Int. J. Geo-Inf. 2016, 5, 128. [Google Scholar] [CrossRef]
- Kada, M.; Luo, F. Generalisation of building ground plans using half-spaces. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2006, 36, 2–5. [Google Scholar]
- Xiao, Y.; Wang, C.; Li, J.; Zhang, W.; Xi, X.; Wang, C.; Dong, P. Building segmentation and modeling from airborne LiDAR data. Int. J. Digit. Earth 2015, 8, 694–709. [Google Scholar] [CrossRef]
- Douglas, D.H.; Peucker, T.K. Algorithms for the reduction of the number of points required to represent a digitized line or its caricature. Cartographica 1973, 10, 112–122. [Google Scholar] [CrossRef]
- Reumann, K.; Witkam, A. Optimizing curve segmentation in computer graphics. In Proceedings of the International Computing Symposium, Davos, Switzerland, 4–7 September 1973; pp. 467–472. [Google Scholar]
- Zhao, Z.; Saalfeld, A. Linear-time sleeve-fitting polyline simplification algorithms. Proc. AutoCarto 1997, 13, 214–223. [Google Scholar]
- Opheim, H. Fast data reduction of a digitized curve. Geo-Processing 1982, 2, 33–40. [Google Scholar]
- Dyken, C.; Dæhlen, M.; Sevaldrud, T. Simultaneous curve simplification. J. Geogr. Syst. 2009, 11, 273–289. [Google Scholar] [CrossRef]
- Kim, C.; Habib, A.; Mrstik, P. New approach for planar patch segmentation using airborne laser data. In Proceedings of the ASPRS, Tampa, FL, USA, 7–11 May 2007. [Google Scholar]
- Weidner, U.; Förstner, W. Towards automatic building extraction from high-resolution digital elevation models. ISPRS J. Photogramm. Remote Sens. 1995, 50, 38–49. [Google Scholar] [CrossRef]
- Jung, J.; Jwa, Y.; Sohn, G. Implicit Regularization for Reconstructing 3D Building Rooftop Models Using Airborne LiDAR Data. Sensors 2017, 17, 621. [Google Scholar] [CrossRef]
- Xu, J.; Wan, Y.; Yao, F. A method of 3D building boundary extraction from airborne LIDAR points cloud. In Proceedings of the IEEE Symposium on Photonics and Optoelectronic (SOPO), Chengdu, China, 19–24 June 2010; pp. 1–4. [Google Scholar]
- Li, M.; Nan, L.; Smith, N.; Wonka, P. Reconstructing building mass models from UAV images. Comput. Graph. 2016, 54, 84–93. [Google Scholar] [CrossRef] [Green Version]
- Sester, M.; Neidhart, H. Reconstruction of building ground plans from laser scanner data. In Proceedings of the AGILE08, Girona, Spain, 4–8 August 2008; p. 111. [Google Scholar]
- Oesau, S.; Lafarge, F.; Alliez, P. Indoor scene reconstruction using feature sensitive primitive extraction and graph-cut. ISPRS J. Photogramm. Remote Sens. 2014, 90, 68–82. [Google Scholar] [CrossRef] [Green Version]
- Poullis, C. A framework for automatic modeling from point cloud data. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 2563–2575. [Google Scholar] [CrossRef]
- Turker, M.; Koc-San, D. Building extraction from high-resolution optical spaceborne images using the integration of support vector machine (SVM) classification, Hough transformation and perceptual grouping. Int. J. Appl. Earth Observ. Geoinf. 2015, 34, 58–69. [Google Scholar] [CrossRef]
- Ley, A.; Hänsch, R.; Hellwich, O. Automatic building abstraction from aerial photogrammetry. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2017, 4, 243–250. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, Y.; Liu, X.; Zhao, Z. 3D building roof reconstruction from airborne LiDAR point clouds: A framework based on a spatial database. Int. J. Geogr. Inf. Sci. 2017, 31, 1359–1380. [Google Scholar] [CrossRef]
- Gross, H.; Thoennessen, U.; Hansen, W.V. 3D modeling of urban structures. Int. Arch. Photogram. Remote Sens. 2005, 36, W24. [Google Scholar]
- Ma, R. Building Model Reconstruction from Lidar Data and Aerial Photographs. Ph.D. Thesis, The Ohio State University, Columbus, OH, USA, 2005. [Google Scholar]
- Gamba, P.; Dell’ Acqua, F.; Lisini, G.; Trianni, G. Improved VHR urban area mapping exploiting object boundaries. IEEE Trans. Geosci. Remote Sens. 2007, 45, 2676–2682. [Google Scholar] [CrossRef]
- Vosselman, G. Building reconstruction using planar faces in very high density height data. Int. Arch. Photogram. Remote Sens. 1999, 32, 87–94. [Google Scholar]
- Zhao, Z.; Duan, Y.; Zhang, Y.; Cao, R. Extracting buildings from and regularizing boundaries in airborne lidar data using connected operators. Int. J. Remote Sens. 2016, 37, 889–912. [Google Scholar] [CrossRef]
- Awrangjeb, M. Using point cloud data to identify, trace, and regularize the outlines of buildings. Int. J. Remote Sens. 2016, 37, 551–579. [Google Scholar] [CrossRef] [Green Version]
- Alharthy, A.; Bethel, J. Heuristic filtering and 3D feature extraction from LIDAR data. Int. Arch. Photogram. Remote Sens. Spat. Inf. Sci. 2002, 34, 29–34. [Google Scholar]
- Li, M.; Wonka, P.; Nan, L. Manhattan-world urban reconstruction from point clouds. In European Conference on Computer Vision; Springer: Cham, Switzerland, 2016; pp. 54–69. [Google Scholar]
- Pohl, M.; Meidow, J.; Bulatov, D. Simplification of polygonal chains by enforcing few distinctive edge directions. In Scandinavian Conference on Image Analysis; Springer: Cham, Switzerland, 2017; pp. 3–14. [Google Scholar]
- Sampath, A.; Shan, J. Building boundary tracing and regularization from airborne LiDAR point clouds. Photogramm. Eng. Remote Sens. 2007, 73, 805–812. [Google Scholar] [CrossRef]
- Guercke, R.; Sester, M. Building footprint simplification based on hough transform and least squares adjustment. In Proceedings of the 14th Workshop of the ICA Commission on Generalisation and Multiple Representation, Paris, France, 3–8 July 2011. [Google Scholar]
- Ikehata, S.; Yang, H.; Furukawa, Y. Structured indoor modeling. In Proceedings of the IEEE International Conference on Computer Vision, Santiago, Chile, 11–18 December 2015; pp. 1323–1331. [Google Scholar]
- Gilani, S.; Awrangjeb, M.; Lu, G. An Automatic Building Extraction and Regularisation Technique Using LiDAR Point Cloud Data and Orthoimage. Remote Sens. 2016, 8, 258. [Google Scholar] [CrossRef]
- Arikan, M.; Schwärzler, M.; Flöry, S.; Wimmer, M.; Maierhofer, S. O-snap: Optimization-based snapping for modeling architecture. ACM Trans. Graph. 2013, 32, 6. [Google Scholar] [CrossRef]
- Monszpart, A.; Mellado, N.; Brostow, G.J.; Mitra, N.J. RAPter: Rebuilding man-made scenes with regular arrangements of planes. ACM Trans. Graph. 2015, 34, 1–12. [Google Scholar] [CrossRef]
- Nan, L.; Jiang, C.; Ghanem, B.; Wonka, P. Template assembly for detailed urban reconstruction. Comput. Graph. Forum 2015, 34, 217–228. [Google Scholar] [CrossRef]
- Favreau, J.; Lafarge, F.; Bousseau, A. Fidelity vs. simplicity: A global approach to line drawing vectorization. ACM Trans. Graph. 2016, 35, 120. [Google Scholar] [CrossRef]
- Wang, J.; Fang, T.; Su, Q.; Zhu, S.; Liu, J.; Cai, S.; Tai, C.; Quan, L. Image-based building regularization using structural linear features. IEEE Trans. Visual. Comput. Graph. 2016, 22, 1760–1772. [Google Scholar] [CrossRef]
- Schnabel, R.; Wahl, R.; Klein, R. Efficient RANSAC for point-cloud shape detection. Comput. Graph. Forum 2007, 26, 214–226. [Google Scholar] [CrossRef]
- Verdie, Y.; Lafarge, F.; Alliez, P. LOD generation for urban scenes. ACM Trans. Graph. 2015, 34. [Google Scholar] [CrossRef]
- Guo, B.; Menon, J.; Willette, B. Surface reconstruction using alpha shapes. In Computer Graphics Forum; Wiley Online Library: Hoboken, NJ, USA, 1997; pp. 177–190. [Google Scholar]
- Avron, H.; Sharf, A.; Greif, C.; Cohen-Or, D. ℓ 1-Sparse reconstruction of sharp point set surfaces. ACM Trans. Graph. 2010, 29, 135. [Google Scholar] [CrossRef]
- Agarwal, S.; Mierle, K. Ceres Solver. 2016. Available online: http://ceres-solver.org/ (accessed on 25 October 2018).
- Kolmogorov, V.; Zabih, R. What energy functions can be minimized via graph cuts? IEEE Trans. Pattern Anal. Mach. Intell. 2004, 26, 147–159. [Google Scholar] [CrossRef] [Green Version]
- Boykov, Y.; Veksler, O.; Zabih, R. Fast approximate energy minimization via graph cuts. Pattern Analysis and Machine Intelligence. IEEE Trans. Pattern Anal. Mach. Intell. 2001, 23, 1222–1239. [Google Scholar] [CrossRef]
- Rottensteiner, F.; Sohn, G.; Gerke, M.; Wegner, J.D. ISPRS test project on urban classification and 3D building reconstruction. In Commission III-Photogrammetric Computer Vision and Image Analysis; Working Group III/4-3D Scene Analysis; 2013; pp. 1–17. Available online: http://www2.isprs.org/tl_files/isprs/wg34/ docs/ComplexScenes_revision_v4.pdf (accessed on 9 December 2018).
- Bentley. Context Capture Create 3D Models from Simple Photographs. 2018. Available online: https://www.bentley.com/en/products/brands/contextcapture (accessed on 25 October 2018).
- Rusu, R.B.; Cousins, S. 3D is here: Point cloud library (PCL). In Proceedings of the 2011 IEEE International Conference on Robotics and automation (ICRA), Shanghai, China, 9–13 May 2011; pp. 1–4. [Google Scholar]
- Zhu, Q.; Li, Y.; Hu, H.; Wu, B. Robust point cloud classification based on multi-level semantic relationships for urban scenes. ISPRS J. Photogramm. Remote Sens. 2017, 129, 86–102. [Google Scholar] [CrossRef]
- Huttenlocher, D.P.; Klanderman, G.A.; Rucklidge, W.J. Comparing images using the Hausdorff distance. IEEE Trans. Pattern Anal. Mach. Intell. 1993, 15, 850–863. [Google Scholar] [CrossRef]
- Rau, J.Y. A Line-based 3D Roof Model Reconstruction Algorithm: Tin-Merging and Reshaping (TMR). ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 3, 287–292. [Google Scholar] [CrossRef]
- Sohn, G.; Jwa, Y.; Jung, J.; Kim, H. An Implicit Regularization for 3D Building Rooftop Modeling Using Airborne LIDAR Data. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2012, 1, 305–310. [Google Scholar] [CrossRef]
- Awrangjeb, M.; Lu, G.; Fraser, C. Automatic Building Extraction from LIDAR Data Covering Complex Urban Scenes. ISPRS Ann. Photogramm. Remote Sens. Spat. Inf. Sci. 2014, 40, 25–32. [Google Scholar] [CrossRef]
















| Area Name | Point Number | Point Density (pt/m2) | Detected Planes (Groups) |
|---|---|---|---|
| Centre | 3,005,398 | 81 | 381 (29) |
| Area Name | Point Number | Point Density (pt/m2) | Detected Planes (Groups) |
|---|---|---|---|
| Area-4 | 1,291,120 | 6.15 | 45 (1) |
| Area-5 | 1,138,977 | 5.42 | 34 (1) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Zhu, Q.; Hu, H.; Wu, B.; Li, Y.; Zhang, Y.; Zhong, R. Hierarchical Regularization of Building Boundaries in Noisy Aerial Laser Scanning and Photogrammetric Point Clouds. Remote Sens. 2018, 10, 1996. https://doi.org/10.3390/rs10121996
Xie L, Zhu Q, Hu H, Wu B, Li Y, Zhang Y, Zhong R. Hierarchical Regularization of Building Boundaries in Noisy Aerial Laser Scanning and Photogrammetric Point Clouds. Remote Sensing. 2018; 10(12):1996. https://doi.org/10.3390/rs10121996
Chicago/Turabian StyleXie, Linfu, Qing Zhu, Han Hu, Bo Wu, Yuan Li, Yeting Zhang, and Ruofei Zhong. 2018. "Hierarchical Regularization of Building Boundaries in Noisy Aerial Laser Scanning and Photogrammetric Point Clouds" Remote Sensing 10, no. 12: 1996. https://doi.org/10.3390/rs10121996
APA StyleXie, L., Zhu, Q., Hu, H., Wu, B., Li, Y., Zhang, Y., & Zhong, R. (2018). Hierarchical Regularization of Building Boundaries in Noisy Aerial Laser Scanning and Photogrammetric Point Clouds. Remote Sensing, 10(12), 1996. https://doi.org/10.3390/rs10121996