Estimation of Forest Canopy Height and Aboveground Biomass from Spaceborne LiDAR and Landsat Imageries in Maryland

Abstract

Mapping the regional distribution of forest canopy height and aboveground biomass is worthwhile and necessary for estimating the carbon stocks on Earth and assessing the terrestrial carbon flux. In this study, we produced maps of forest canopy height and the aboveground biomass at a 30 m spatial resolution in Maryland by combining Geoscience Laser Altimeter System (GLAS) data and Landsat spectral imageries. The processes for calculating the forest biomass included the following: (i) processing the GLAS waveform and calculating spatially discrete forest canopy heights; (ii) developing canopy height models from Landsat imagery and extrapolating them to spatially contiguous canopy heights in Maryland; and, (iii) estimating forest aboveground biomass according to the relationship between canopy height and biomass. In our study, we explore the ability to use the GLAS waveform to calculate canopy height without ground-measured forest metrics (R² = 0.669, RMSE = 4.82 m, MRE = 15.4%). The machine learning models performed better than the principal component model when mapping the regional forest canopy height and aboveground biomass. The total forest aboveground biomass in Maryland reached approximately 160 Tg. When compared with the existing Biomass_CMS map, our biomass estimates presented a similar distribution where higher values were in the Western Shore Uplands region and Folded Application Mountain section, while lower values were located in the Delmarva Peninsula and Allegheny Mountain regions.

1. Introduction

Increasing concerns regarding global climatic changes have emphasized the urgency of finding efficient ways to quantify terrestrial carbon stocks at regional, continental, and global scales [1]. Forest biomass is of primary importance for the assessment and management of carbon resources on Earth. At the same time, changes in forest biomass can be a good proxy for the analysis of the global carbon cycle and a valid resource for the estimation of sequestration and carbon sources/sinks [2,3]. Scientific researchers also use forest biomass to study ecosystem biodiversity [4,5]. In recent years, efforts have been made to mitigate the deforestation and emissions of greenhouse gases. Such forest biomass studies will record valuable information that can be used to evaluate the effects of these efforts. Furthermore, it is helpful to provide governments with constructive suggestions for biodiversity conservation and ecosystem management. Hence, it is strongly necessary to explore an efficient approach to assess forest biomass at regional, continental, and even global scales.

Field forest measurements provide a straightforward, accurate method in order to calculate the amount of terrestrial aboveground forest resources and evaluate the global carbon cycle [6]. Tree metrics, such as height, DBH (diameter at breast height), tree age, tree species, and LAI (leaf area index) can link forest biomass estimates with allometric relationships [7,8,9,10]. Nevertheless, ground inventory campaigns require huge investments of labor, time, and money, which result in inconsistency over large regions and the lack of ground-based inventories in remote areas.

LiDAR is another method to link forest height and other biophysical characteristics. It can be used to make digital three-dimensional (3D)-representations of the target and high-resolution maps with wide applications in forestry [11,12,13]. Tree heights obtained by airborne LiDAR have proven to be a good predictor of forest biomass [14]. Naesset and Goabakken explained 88% and 85% of the variability in aboveground and belowground biomass, respectively, using airborne LiDAR [15]. Drake et al. explored the sensitivity of LiDAR to differences in canopy structure and aboveground biomass in a dense, neotropical rainforest [16]. However, the application of airborne LiDAR to forest biomass also has challenges as airborne LiDAR relies heavily on financial support and does not cover the global surface. Thus, researchers have turned to Earth observation satellites to obtain nearly real-time overviews of the terrestrial carbon stocks [17]. The NASA (National Aeronautics and Space Administration) GLAS (Geoscience Laser Altimeter System) instrument, on board the ICESat (Ice, Cloud and Land Elevation Satellite) records the full waveforms of detected footprints (~65 m on the surface of Earth), which provide vertical information of the surface of the Earth, including vegetation [18,19]. The GLAS waveform has demonstrated tremendous potential in calculating forest canopy heights and biomasses even though it was designed with the primary objective of monitoring polar ice sheets. One of the distinct superiorities of GLAS data is that we are able to acquire tree heights within a single footprint, which makes it a valuable supplement to field inventories. Therefore, the ICESat potentially supports the study of terrestrial carbon resources, especially in remote areas that humans are unable to reach. However, GLAS data, which are distributed as scattered points, cannot provide spatially contiguous records. Thus, interpolation processes, such as the kriging method [20,21,22] or spatially continuous optical imagery, are included to produce regional forest biomass estimates [23,24,25,26,27,28,29,30,31].

Multispectral sensors record the information from visible light to short wave infrared light, and red and near-infrared light are sensitive to vegetation. Therefore, spectral imagery offers another resource for estimating forest aboveground biomass. Landsat sensors provide 16-day repeat coverage of the surface of the Earth with a spatial resolution of 30 m. Numerous studies have proven the feasibility of using Landsat data to survey forest resources and monitor the changes in terrestrial carbon stocks [32,33,34,35,36,37,38].

NASA is planning to launch ICESat-2 and GEDI (The Global Ecosystem Dynamics Investigation) in 2018; ESA (The European Space Agency) will launch BIOMASS in 2020. These missions will provide great supports for the research of forest biomass and carbon cycle. Therefore, it is necessary to study efficient methods of evaluating forests to service further research. The main purpose of this paper was to analyze and compare the performances of the principal components model and three machine learning models, including BPANN (backpropagation artificial neuronal network), SVR (support vector regression), and RF (random forest) for estimating the forest biomass. Our basic processes were (i) to compute the forest canopy height within discrete GLAS footprints using the full waveform parameter; (ii) to link the canopy height produced by GLAS with the vegetation indexes and then establish the principal component model and machine learning models to map spatially contiguous canopy heights; and, (iii) to develop a power equation from the forest canopy heights to estimate the aboveground biomass. Finally, we compare our estimates to other existing forest aboveground biomass values in Maryland and explain why our method has potential at larger scales.

2. Study Area and Datasets

2.1. Study Area

Maryland (37.8°N–39.8°N, 75.0°W–79.5°W) lies in the mid-Atlantic region of the United States, bordering Virginia and Washington to the south and west and covering a land area of ~25,600 km² [39]. The east of Maryland is relatively flat with elevations from 0–200 m and has a humid subtropical climate, with hot, humid summers and short, cool winters, while the opposite region around the Appalachian Mountains is higher and more complicated with elevations from 150–900 m and has a humid continental climate. The rainfall in Maryland ranges from 890–1140 mm and is even greater at higher elevations. Maryland is divided into 24 counties when considering the political functions, and it can also be separated into nine physical regions when natural elements, such as location, topography, and climate are concerned (Figure 1a). Overall, Maryland has a wide array of climates due to the variances in the elevation and proximity to water.

Maryland possesses abundant forest resources, and the forested lands account for 42.8% of the total land cover in spite of the urbanization that occurred by 2000 [40]. From the forest distribution map produced by the MRLC (Multi-Resolution Land Characteristics Consortium (Figure 1b)), it is apparent that Maryland is dominated by deciduous forest apart from the evergreen forests in the southeast and there are only minimal mixed forests in the western shore upland region. It is the wide variabilities in the topography and natural environment and the abundant forest resources that make Maryland a suitable place to study forest biomass.

2.2. ICESat GLAS Laser Altimetry Data

The GLAS instrument was mounted on the Ice, Cloud and Land Elevation Satellite (ICESat) and was the first satellite-based earth orbiting laser altimeter that was part of the Earth Observing System (EOS) of NASA and was operational from January 2003 to October 2009 [41]. Even though the primary purpose of the ICESat mission was to take ice sheet elevation measurements in the polar regions [42], GLAS data have been widely applied to accurately map regional, continental, and global vegetation heights and carbon volumes with active pulse emission/reception [43]. The laser altimeters provide the range between the spacecraft and the illuminated spot on the surface of the Earth by measuring the round-trip travel time of the laser pulse. The GLAS sensor acquires altimetry information at 1064 nm with 40 Hz lasers, which consequently leave nominal ~65 m diameter footprints and ~170 m intervals between spots [44].

GLAS laser altimeter data can be downloaded from the National Snow and Ice Data Center (NSIDC) website (https://nsidc.org/data/icesat). The database provides 15 Level-1 and Level-2 data products (GLA01 to GLA15), and the GLA01 and GLA14 products were used in this study. The instrument determines the range by measuring the time between the emission of the laser pulse and the detection of the photons reflected from the surface of the Earth. The detected pulse is digitized in 1ns (15 cm) range bins. From a total of 1000 selected range bins, a smaller number 544 over land and ice sheets and 200 over oceans and sea ice regions was selected for transmission. The corresponding range widths of the transmissions were 81.5 m and 30 m. What requires more attention is that the size from 1 to 151 bins is prolonged to 4 ns (60 cm), starting from L3A; therefore, the length of the corresponding waveform increases to 150 m [45,46]. GLA01 is a level 1A product and records the actual waveform. GLA14 is a level 2 land product and contains other crucial information on the footprints, such as the elevation (i_elev), latitude (i_lat), longitude (i_lon), transmission time of the first shot in the frame in J2000 (i_UTMTime), start and end range increment of the signal (i_SigBegOff, i_SigEndOff), signal saturation index (i_satNdx), standard deviation of the background noise (i_sDevNsObl), max amplitude of the received echo (i_maxRecAmp), likely presence of clouds (i_Frir_qaFlag), amplitude of the Gaussian distribution (i_Gamp), sigma of the Gaussian distribution (i_Gsigma), and the centroid range increment for the Gaussian fits (gpCntRngOFF). Sun et al. demonstrate that the six Gaussian distributions have a strong relationship with the vertical features of the forest and the underlying topography [47].

In this study, we downloaded all year round GLAS data in Maryland from 2005–2008 to maintain consistency with the validation data. Then, we extracted the data from the raw GLAS file using the IDL tools provided by the NSIDC. Next, it was necessary to filter out invalid data according to the parameters of GLA14. We deleted all of the contaminated points when i_satNdx exceeded 2 or the SNR (signal-to-noise ratio = i_maxRecAmp/ i_sDevNsObl) was less than 60. At the same time, we only retained the cloud-free footprint when the i_Frir_qaFlag was equal to 15. We also used NLCD 2011 (National Land Cover Database 2011) to select points, which were within forest areas in Maryland. Finally, the selected dataset contained a total of 2720 valid GLAS records (Figure 1b). The laser campaigns we used in this study included 3B, 3C, 3D, 3E, 3G, 3H, 3I, 3J, and 3K. The ICESat elevation corresponded to the TOPEX/Poseidon ellipsoid; so, we converted it into WGS84 to maintain consistency with other data. After that, the GLAS waveforms needed to be filtered using wavelet transformation to eliminate sharp noise. Furthermore, a critical step was to decompose the GLAS waveform into multiple Gaussian distribution curves, as described in previous studies [17,47,48]. Finally, we quantified the background noise by calculating the mean value and standard deviation of the background signal, and then we set thresholds to identify the start and end of the signal. The start noise and end noise presented different characteristics, so we dealt with them separately. Usually, the threshold is defined as the mean value plus n times of the standard deviation. However, the value of n varies in different studies (n = 3 [47], n = 3.5 [49], n = 4 [50], n = 4.5 [51]). In this study, n = 3 was used. Furthermore, we also calculated the slope index [52] within each footprint to reduce the impact of terrain.

2.3. CMS_RF Forest Canopy Height and Aboveground Biomass for Maryland

The CMS (Carbon Monitoring System) forest canopy height and aboveground biomass data, as part of the NASA CMS plan, are accessible from the ORNL DAAC (The Oak Ridge National Laboratory Distributed Active Archive Center) CMS website (https://daac.ornl.gov/cgi-bin/dsviewer.pl?ds_id=1320). The NASA CMS is designed to make significant contributions to characterizing, quantifying, and predicting the evolution of global carbon sources and sinks by improving the monitoring of carbon stocks and fluxes. This dataset provided a 30-m gridded estimation of canopy height and aboveground biomass for the state of Maryland in 2011 [53]. The tree canopy height was modeled by high-resolution (one meter) airborne LiDAR, which is then aggregated to a height distribution of 30 m [54]. The aboveground biomass map was produced by combining the leaf-off LiDAR data with file allometric estimates from 848 variable plots across Maryland. Field-based estimates were then related to the LiDAR height and volume metrics using random forest regression models to generate a statewide biomass map. The aboveground biomass map explained ~50% of the variability when compared with the field plots (R² = 0.49, RMSE = 89.3 Mg ha⁻¹, n = 848), and was then cross validated with FIA (forest inventory and national analysis program) data that showed better agreement (R² = 0.69, RMSE = 58.2 Mg ha⁻¹, n = 1055). More details of the canopy height and aboveground biomass are available in [39,55].

2.4. Landsat Data

The Landsat program is co-managed by NASA and USGS (United States Geological Survey) and provides the longest continuous records to help policymakers and land managers to make wise and farsighted decisions regarding global resources and the environment. Multi-temporal data ensures the possibility of downloading cloud-free, high quality, and atmospherically uncontaminated imageries covering the entire state [56]. The TM (Thematic Mapper) and ETM+ (Enhanced Thematic Mapper Plus) data record information from visible to infrared light, which has been proven in previous studies as qualified to distinguish different land cover types or even vegetation types with different volumes [57,58,59,60,61]. Powell et al. modeled live aboveground biomass using Landsat satellite imagery and derived the trajectories of the biomass dynamics in Arizona and Minnesota [62]. Liu et al. built an algorithm to estimate the forest aboveground biomass using TM data, which provided a reliable estimate (R² = 0.71, RMSE = 39.60 Mg ha⁻¹) in the Changbai Mountains [24].

We downloaded surface reflectance data products that had been atmospherically corrected, from the USGS website (https:earthexplorer.usgs.gov). In this study, the data included six scenes of TM imagery (P14R33_20090521, P14R34_20090521, P15R32_20110603, P15R33_20100429, P16R32_20090519, and P16R33_20090519) and two scenes of ETM+ imagery (P17R32_20090518, and P17R33_20090518), which were acquired during the vegetation growing period in this study. The products were mapped in World Geodetic System (WGS) 84 datum and the Universal Transverse Mercator (UTM) projection.

2.5. National Land Cover Database 2011

We downloaded the NLCD 2011 from https://www.mrlc.gov.nlcd2011.php. The data are the most recent national land cover product created by the MRLC Consortium. The product uses Landsat imagery as the primary data resource and has a spatial resolution of 30 m. The database classifies the national surface into 20 land cover types, and deciduous forest, evergreen forest, and mixed forest constitute the American forest. The overall accuracies of NLCD 2011 was 88% [63]. The NLCD 2011 has been recognized as an important source to analyze carbon cycle problems within certain land cover types at both the regional and national scales [64]. The CMS_RF forest canopy height and the aboveground biomass introduced in Section 2.3 were also calculated with the help of the NLCD.

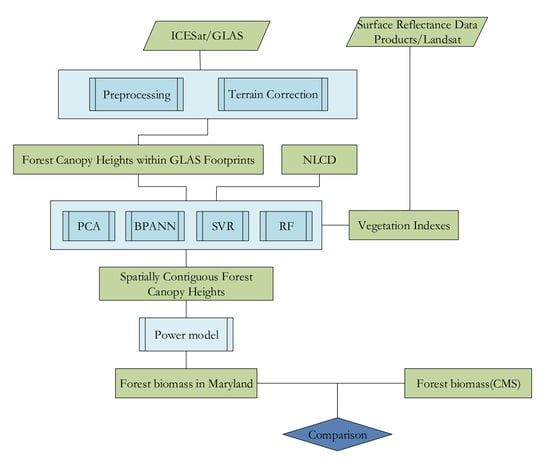
3. Methods

3.1. Estimating Forest Canopy Height from the GLAS Waveform

After the preprocessing steps described in Section 2.2, we extracted several key variables (Figure 2) needed to calculate the forest canopy height and biomass from the GLAS waveforms. Even though the GLA14 product contains information that can be used to identify these critical parameters, we chose to define the key positions through a series of algorithms when considering the underlying noise in the GLA14 data [49]. The total waveform length, which is the distance from signal start to signal end, contains all of the vertical height information in the vegetation region and even includes some topographic slope noise [18]. The signal start and end were determined using the start and end thresholds acquired by the preprocessing steps. The last peak was regarded as the ground peak only if the amplitude was higher than those of the nearby peaks and the distance between the selected peak and the signal end exceeded the half width of the laser pulse (60 cm) [18,65,66]. The centroid of the waveform records the half energy from the signal start to the ground peak. The trailing edge extent was determined as the difference between the signal end and the last bin where the signal intensity of the waveform is half the maximum intensity. In this study, we calculated the distance from the signal start to the ground peak as the canopy height, and then added the terrain index to optimize the canopy height within GLAS footprint.

An approach developed by Mahoney [52] for calculating the slope from GLAS was applied for terrain correction. We used a simple way to calculate the slope ($\mathsf{\theta }$) within each GLAS footprint with Equation (1).

$$\mathsf{\theta }=\mathrm{atan}(\frac{2\ast Trai{l}_{ext}}{d})$$

(1)

where $Trai{l}_{ext}$ is the trailing edge extent; and $d$ is the mean diameter for the GLAS footprint.

In this process, $Trai{l}_{ext}$ was directly used as the terrain index. We built a linear formula to combine the maximum canopy height and terrain index to improve the accuracy of the estimated canopy height.

3.2. Extrapolating Canopy Height to the Study Area

Using the GLAS waveform to supplement field inventory data is a significant method to evaluate the forest volume and carbon stocks at regional and global scales. However, the GLAS data are scattered over the study area, so it is necessary to combine these data with spectral imageries (Landsat imageries) to produce a spatially contiguous canopy height map. The size of a GLAS footprint is approximately 65 m, while the resolution of Landsat imagery is 30 m. Thus, we upscaled the spectral data to 60 m, and then built relationships between the forest canopy height and the vegetation indexes. Next, we applied the relationships to the non-upscaled imageries. In total, we selected five vegetation indexes, the NDVI (normalized difference vegetation index) [67,68,69], EVI (enhanced vegetation index) [68], RVI (ratio vegetation index) [70], DVI (difference vegetation index) [69], and the VARI (visible atmospherically resistant index) [71].

In order to take into account all the vegetation indexes, we conducted PCA (principal components analysis), machine learning models (BPANN, SVR, and RF) to estimate the spatially contiguous canopy height.

PCA is a statistical procedure that uses an orthogonal transformation to convert a set of observations of possibly correlated variables into a set of values of linearly uncorrelated variables called principal components. These new components are linear combinations of the original variables [72,73,74]. The first principal component has the largest possible variance (that is, accounts for as much of the variability in the data as possible), and each succeeding component in turn has the highest variance possible under the constraint that it is orthogonal to the preceding components. The resulting vectors are an uncorrelated orthogonal basis set. Thus, PCA is often used in data reduction to identify a small number of factors that can explain most of the variances.

The BPANN algorithm consists of forward-propagation of the data stream and back-propagation of the error signal. For the forward propagation, the direction is input layer→hidden layer→output layer, and each layer determines the next layer. If the results fail to meet the expected output, the error signal helps adjust the data stream in reverse [75]. BPANN is sensitive to the number of neurons in hidden layers and the type of activation functions for the layers [76]. In this process, Matlab toolboxes were used to train the models. We chose three categories of transfer functions: the tansig (hyperbolic tangent sigmoid), logsig (log-sigmoid), and purelin (linear) transfer function. The tansig transfer function can produce both positive and negative values, which tends to yield faster training than the logsig transfer function, which produces only positive values. In terms of training algorithms, we chose traingd, traingdx, trainingda, trainrp, trainlm, trainbfg, trainscg, trainoss, traincgf, and traincgp. More detailed information of these training algorithms is available in [77].

The SVR is a version of SVM (support vector machine) for regression. Its basic idea is to minimize the structural risk and keep the target as flat as possible [78]. The main design of a SVR model is the kernel, which is an inner product in the SVR feature space. Since inner products induce distance metrics and vice versa, the basic goal in SVR kernel design is to find an appropriate metric in the SVR feature space relevant to the regression problem [79]. The Libsvm toolbox supports two kinds of formulations for regression. In this study, we trained ν-SVR [80] and ε-SVR [81], and chose linear, polynomial, and RBF (Radial Basis Function) kernels.

Random forest is an ensemble learning method that constructs a multitude of decision trees and then outputs a mean prediction regression of the individual trees [82]. RF takes advantage of two powerful machine learning techniques: bagging and random feature selection. In bagging, each tree is trained on a bootstrap sample of the training data, and predictions are determined by the majority vote of the trees. It performs a type of cross-validation in parallel using the so-called out-of-bag samples to assess the predictions [83]. In this research, we changed the number of trees and the features randomly selected in each node of each tree in order to optimize the model.

Furthermore, to avoid overfitting, we conducted 10-fold cross validation to analyze the result of each model.

3.3. Estimating Forest Aboveground Biomass in Maryland

Forest canopy height provides a crucial indicator to calculate the forest aboveground biomass. Several studies have studied the relationships between canopy height and biomass [1,51,84]. In this section, we extracted forest canopy height and biomass from CMS maps within GLAS shot locations, and then developed a power model from forest canopy height to biomass. Similarly, 1800 points were used to establish the model and 920 points were used to validate the model.

4. Results

4.1. GLAS Waveform to Forest Canopy Height

After preprocessing the GLAS waveform data and identifying the key parameters, we obtained 2720 forest canopy heights in Maryland. Figure 3a shows the results of the simple canopy height method (R² = 0.606, RMSE = 4.78 m, MRE = 15.9%).

Furthermore, we also used 1820 points to establish a linear empirical relationship (Equation (2)) in order to optimize canopy height ($\mathrm{H}$).

$$\mathrm{H}=H_{max}-0.73\ast Trai{l}_{ext}$$

(2)

where $H_{max}$ presents the distance between the signal start and ground peak.

Figure 3b illustrates the evaluation result of the terrain corrected canopy height by the remaining 900 points (R² = 0.669, RMSE = 4.82 m, MRE = 15.4%). This result indicates that the method in this study was qualified and reliable, and terrain correction could improve the estimation accuracy. In previous studies, Lee et al. [85] and Cao et al. [86] conducted slope correction by $\mathrm{H}=H_{max}-0.5\ast d\ast \tan \left(\theta \right)$, which was similar to ours. Therefore, we considered the equation to be reliable for the slope correction.

4.2. Extrapolating Canopy Height to the Study Area

When considering the high correlations between vegetation indexes, PCA was first conducted to reduce the number of variances. We extracted the principal components if the corresponding eigenvalue exceeded 1. Finally, only the first principal component was selected. Figure 4 shows the relationship between the first principal component and canopy height.

We also trained 22 BPANN models, four SVR models, and 11 RF models to estimate the forest canopy height. Appendix

Table A1. Results (R²) using different parameters in the BP-ANN model.

Cross Validation	no.1	no.2	no.3	no.4	no.5	no.6	no.7	no.8	no.9	no.10	Average Value
5,t,l,tlm	0.441	0.328	0.439	0.422	0.443	0.322	0.423	0.479	0.340	0.289	0.392
8,t,l,tlm	0.427	0.420	0.453	0.399	0.438	0.406	0.396	0.411	0.341	0.299	0.399
20,t,l,tlm	0.234	0.362	0.497	0.430	0.435	0.411	0.270	0.426	0.326	0.265	0.366
50,t,l,tlm	0.308	0.246	0.563	0.239	0.240	0.377	0.207	0.330	0.238	0.251	0.300
8,t,t,tlm	0.418	0.383	0.473	0.435	0.452	0.438	0.402	0.408	0.330	0.310	0.405
8,t,l,tlm	0.461	0.409	0.454	0.446	0.409	0.414	0.385	0.451	0.286	0.337	0.405
8,l,t,tlm	0.413	0.398	0.464	0.424	0.437	0.418	0.381	0.268	0.345	0.290	0.384
8,l,l,tlm	0.468	0.368	0.457	0.402	0.458	0.419	0.376	0.393	0.328	0.307	0.398
8,l,p,tlm	0.481	0.434	0.425	0.439	0.440	0.433	0.409	0.500	0.373	0.352	0.429
8,p,t,tlm	0.461	0.403	0.430	0.438	0.442	0.436	0.383	0.485	0.339	0.326	0.414
8,p,l,tlm	0.214	0.436	0.420	0.413	0.434	0.438	0.417	0.430	0.321	0.339	0.389
8,p,p,tlm	0.468	0.413	0.391	0.401	0.403	0.414	0.418	0.457	0.350	0.328	0.404
8,t,l,tgd	0.408	0.051	0.287	0.217	0.206	0.321	0.216	0.301	0.013	0.256	0.228
8,t,l,tgdx	0.448	0.412	0.382	0.396	0.408	0.400	0.408	0.469	0.344	0.352	0.402
8,t,l,tgda	0.462	0.407	0.372	0.373	0.370	0.424	0.397	0.423	0.339	0.306	0.387
8,t,l,trp	0.477	0.426	0.422	0.445	0.432	0.436	0.421	0.481	0.357	0.345	0.424
8,t,l,tlm	0.449	0.402	0.446	0.439	0.422	0.408	0.381	0.454	0.338	0.335	0.407
8,t,l,tfg	0.463	0.429	0.435	0.455	0.436	0.442	0.423	0.470	0.375	0.351	0.428
8,t,l,tcg	0.478	0.427	0.427	0.443	0.419	0.436	0.418	0.469	0.345	0.364	0.423
8,t,l,tss	0.480	0.425	0.422	0.439	0.421	0.444	0.414	0.452	0.363	0.357	0.422
8,t,l,tgf	0.470	0.365	0.425	0.347	0.427	0.443	0.417	0.478	0.352	0.352	0.408
8,t,l,tgp	0.401	0.433	0.406	0.412	0.433	0.434	0.409	0.476	0.359	0.355	0.412

5, 8, 20, 50 represent the the number of neurons in hidden layers; t, l, p represent the tansig, logsig, and purelin transfer function; tgd, tgdx, tgda, trp, tlm, tfg, tcg, tss, tgf, tgp represent traingd, traingdx, trainingda, trainrp, trainlm, trainbfg, trainscg, trainoss, traincgf, and traincgp training algorithms, respectively. The bold were the experiments with the best validation results.

summarizes the BPANN performances (R²) using different numbers of neurons, transfer functions, and training algorithms. Generally, all of the BPANN models obtained similar performance results. It can be seen that eight neurons-model performed best, while 50 neurons-model gained a poor result. The different transfer functions and training algorithms seemingly had few effects on the results, except for the training algorithm of traingd. The best BPANN model was constructed by eight neurons, logsig, and purelin transfer functions, and a trainlm training algorithm. Appendix

Table A2. Results (R²) using different parameters in the SVR model.

Cross Validation	no.1	no.2	no.3	no.4	no.5	no.6	no.7	no.8	no.9	no.10	Average Value
-s 4 -t 2 -c 1 -g 1 -n 0.5	0.477	0.418	0.405	0.416	0.383	0.414	0.406	0.466	0.336	0.332	0.405
-s 3 -t 0 -c 1 -g 1 -p 0.1	0.468	0.410	0.389	0.400	0.401	0.413	0.419	0.452	0.350	0.328	0.403
-s 3 -t 1 -c 1 -g 1 -p 0.1	0.455	0.378	0.379	0.394	0.418	0.406	0.379	0.427	0.363	0.339	0.394
-s 3 -t 2 -c 1 -g 1 -p 0.1	0.471	0.425	0.410	0.422	0.389	0.426	0.412	0.466	0.330	0.344	0.409

-s 3, -s 4 represent ε-SVR and ν-SVR; -t 0, -t 1, -t 2 represent the linear, polynomial and RBF kernels; -c represents the cost function; -g represents the gamma function; and -p and -n are the parameters in cost function for ε-SVR and ν-SVR respectively. We used defaults for -c, -g, -p and -n. The bold were the experiments with the best validation results.

illustrates the SVR performances using different SVR formulations and kernels. This showed that these SVR models obtained nearly the same performances, and the model with ε-SVR, RBF kernel performed better than the others. Similarly, few variations were seen in different RF models. Appendix

Table A3. Results using different parameters in the RF model.

Cross Validation	no.1	no.2	no.3	no.4	no.5	no.6	no.7	no.8	no.9	no.10	Average Value
10_2_1	0.407	0.376	0.655	0.432	0.416	0.402	0.389	0.435	0.409	0.396	0.432
50_2_1	0.480	0.410	0.689	0.459	0.439	0.418	0.393	0.468	0.456	0.409	0.462
100_2_1	0.482	0.419	0.700	0.469	0.442	0.417	0.398	0.471	0.452	0.420	0.467
200_2_1	0.478	0.424	0.704	0.475	0.442	0.424	0.395	0.476	0.449	0.418	0.468
500_2_1	0.478	0.423	0.707	0.473	0.446	0.428	0.396	0.482	0.445	0.423	0.470
1000_2_1	0.480	0.423	0.706	0.475	0.445	0.430	0.396	0.482	0.443	0.423	0.470
100_1_1	0.481	0.419	0.693	0.470	0.451	0.424	0.392	0.474	0.440	0.412	0.466
100_3_1	0.472	0.414	0.708	0.465	0.439	0.414	0.393	0.487	0.438	0.427	0.466
100_4_1	0.461	0.415	0.712	0.447	0.447	0.413	0.399	0.476	0.432	0.429	0.463
100_5_1	0.457	0.421	0.713	0.445	0.429	0.411	0.388	0.474	0.434	0.424	0.460
100_2_0	0.472	0.414	0.707	0.465	0.429	0.411	0.395	0.486	0.440	0.428	0.465

10, 50, 100, 200, 500, 1000 represent the number of trees; 1, 2, 3, 4, 5 in the second parameter represent the features randomly selected in each node of each tree; and 1, 0 in the third parameter represent calculating the importance or not. The bold were the experiments with the best validation results.

demonstrates that the more trees gained better results, and when the number of features randomly selected in each node of each tree was 2, the result was better.

Next, we respectively chose the best model to analyze the performances of three machine learning models. The evaluation results (Figure 5) indicated that machine learning models could potentially be used to estimate forest canopy heights from spectral imagery. The three methods performed similarly with R² values from 0.42 to 0.46, RMSE values from 3.71 m to 4.11 m, and MRE values from 10.6 to 11.96%, and the RF model reached the most acceptable agreement with the validated canopy height from GLAS (R² = 0.46, RMSE = 3.71 m, MRE = 10.6%). However, there was a common limitation where the canopy height estimates were lower than the validated values in the high canopy height areas (greater than 35 m), while the canopy height estimates were higher in the low canopy height areas (less than 15 m). Namely, most estimates were inclined to fall in a median area, which usually resulted from the machine learning model.

Next, we applied the first principal component power model and three machine learning models to the entirety of Maryland. Figure 6 demonstrates that these four models performed similarly even though there were subtle differences. Overall, the forest canopy height was relatively high at 30–50 m within the Western Shore Uplands region and Folded Application Mountain section, while it was lower at 10–20 m in the Blue Ridge province and Allegheny Mountain section. The trees with extremely low canopy heights (0–10 m) were scattered at the edges of the forest instead of being aggregating into blocks. The Lowland and Upland sections were made up of median forest heights (10–30 m). From the distribution of these models, machine learning models performed better than the first principal component power model that produced canopy height concentrated at 20–40 m and showed few local variations. However, machine learning models require significant additional costs in terms of time, effort, and computational resources.

4.3. Forest Canopy Height to Aboveground Biomass

In this section, we developed a general model to estimate forest biomass from the spatially contiguous canopy height data throughout Maryland. Figure 7 demonstrates that the biomass and canopy height in Maryland are closely linked, and the evaluation results were satisfactory (R² = 0.70, RMSE = 35.81 Mg/ha, MRE = 17.0%). Cao [86] and Lefsky [50] discussed biomass estimation models in their studies, and our equation was similar to those in the previous studies. Therefore, we considered the equation to be valuable and reliable for biomass estimation in Maryland.

As shown in Figure 8, the forest aboveground biomass ranged from 0–400 Mg/ha. As we estimated the forest aboveground biomass using a direct, univariate power model, the distribution of the biomass resembled the canopy heights. The forest biomass in the Western Shore Uplands region and Folded Application Mountain section was higher. In contrast, the lower biomass forests were distributed in the Blue Ridge province and Allegheny Mountain regions. Similarly, the first principal component model failed to distinguish the high biomass and low biomass areas. After taking the model evaluation results described in Section 3.2 and the forest biomass distribution described in this section into comprehensive consideration, we suggest that the RF estimate was the best.

4.4. Comparing Biomass Estimates to Other Data Resources

In this section, we compared our forest biomass maps with Biomass_CMS in terms of the distribution and quantity. As introduced in Section 2.3, the forest Biomass_CMS in Maryland was produced by the NASA CMS using LiDAR and allometric estimates with small footprints. Overall, our biomass estimates shared a similar distribution with Biomass_CMS, where higher values were obtained in the Western Shore Uplands region, while lower values were located in Blue Ridge province and Allegheny Mountain region. However, the Biomass_CMS appeared more scattered with low biomass flecks due to the land cover errors. The non-forest, which was mistakenly regarded as forest, may be identified as high biomass, according to the spectral information (the biomass data source in this study), while the Biomass_CMS was small when considering the lower airborne LiDAR values (the Biomass_CMS data source). Figure 9 demonstrates the distribution of forest biomass difference between the biomass estimated by RF and Biomass_CMS in Maryland. It can be seen that 53% of the absolute difference of forest biomass were less than 50 Mg/ha, and 85% for 100 Mg/ha. In this map, positive values represent that the Biomass_RF exceeded the Biomass_CMS. Our method overvalued the forest biomass in the Folded Application Mountain section and southern areas in the Upland section. The areas where the difference exceeded 100 Mg/ha took up around 10% of the total forest in Maryland. On the other hand, our model underestimated the forest biomass in some small areas of the Allegheny Mountain region, Upland section, and Western Shore Upland region.

Next, the forest biomass in each physical region and political county were statistically compared to quantitatively analyze the biomass distribution. Figure 10 presents the forest aboveground biomass (Tg) in each county and physical region and the total values throughout Maryland. The estimates from all of the models had parallel tendencies. Garrett and Allegany counties had the most abundant forest resources (more than 15 Tg) due to the large forest areas, followed by Charles, Baltimore, and Frederick counties (more than 10 Tg). In contrast, there were five counties (Worcester, Talbot, Dorchester, Somerset, and Baltimore City) where the forest aboveground biomass was less than 3 Tg. When analyzing the biomass based on the physical regions, distinct characteristics were recognized. The forest biomass in the Western Shore Uplands region (approximately 45 Tg) constituted 30% of the total forest aboveground biomass in Maryland, which was far more than that in other regions. In contrast, the Great Valley section and the Western Shore Lowlands region contained the least forest, around 3Tg. Following the Western Shore Uplands region, the upland section had the second highest forest biomass (nearly 35 Tg). Then, the Allegheny Mountain section, Delmarva Lowlands region, and Folded Appalachian Mountains section followed, where the forest resources were similarly rich (approximately 20 Tg). In addition, the Blue Ridge Province and the Lowland section made petty contributions to the forest biomass in Maryland.

The total biomass in the state of Maryland reached approximately 160 Tg (Figure 10). Generally, our models all overvalued the total forest biomass in Maryland. The BPANN method gained the highest estimate with 171 Tg, while the SVR estimate was comparatively lower with 166.2 Tg, which most likely resulted from the underestimation of some areas.

5. Discussion

We estimated the forest canopy height and aboveground biomass in the state of Maryland by combining spaceborne LiDAR, spectral imageries, and forest resource data produced by NASA. The results showed the capacity of our approach for regional-scale forest biomass estimation and allowed us to evaluate the various sources of error and uncertainty.

5.1. Processing the GLAS Waveform

The GLAS waveform provides a crucial approach to calculate forest parameters, such as canopy height, especially without any tree metrics. Even though the GLAS records the waveform along only the narrow flight lines, it still presented a strong ability to extract valuable forest parameters, which has also been proven in a large number of studies. We estimated the canopy height from GLAS by calculating the distance from the start of the signal to the ground peak and added the terrain index to optimize the canopy height. Then, a regression was run between the estimated canopy height from the GLAS waveform and the canopy height from the NASA CMS with an acceptable result (R² = 0.669, RMSE = 4.82 m, MRE = 15.4%). Nevertheless, the result also suggests that future efforts need to focus on forming a better relationship.

In Section 3.1, we introduced a series of Gaussian parameters within the GLA14 product that could be used to estimate the canopy height. Gaussian parameters always include mass noise, so they may fail to reliably estimate the canopy height. Thus, we utilized a different method in this study. The procedure comprised preprocessing the GLAS waveform, identifying critical parameters, and, adding the terrain index to optimize canopy height. Even though we filtered out invalid GLAS points, some still failed to produce the desired canopy height. The error may be caused by the fact that each GLAS laser had different pulse intensities. If we deal with all of the GLAS data using the same method, some may lead to errors. We can separately process waveform according to GLAS laser in future study. Furthermore, to gain a large number of the GLAS data, we did not filter out the points that were recorded within leaf off periods. This may be another error source.

5.2. Extrapolating to A Larger Spatial Scale with Spectral Images

The extrapolation process described in this article was used to establish the first component model and machine learning models between the canopy height estimated from GLAS and the vegetation indexes from spectral imageries. Therefore, the quality of the spatially contiguous canopy height heavily depended on the spectral imageries. In this study, we first upscaled the Landsat data to 60 m to keep it spatially consistent with the GLAS waveform data, and then the model that was established at the upscaled resolution was used to estimate the spatially continuous canopy height at the original resolution of 30 m. A scale effect may exist between the remote sensing data of different spatial resolutions, which might cause an error when applying the relationship built from 60 m resolution data to 30 m resolution data. The study area was covered by eight Landsat imagery scenes. Even though we selected images that were as close as possible during the vegetation growing season, there were still variations in the acquisition time. Due to the different phenophases of the forest in different images, the vegetation index that corresponded to the same biomass value might present different records in different images. That is, using the same formula to estimate biomass over multiple scene images is likely to introduce an error. Furthermore, the difference in the spectral bandpass of Landsat5 and Landsat7 may introduce errors, as it leads to a difference performance between the indices that we used to estimate forest biomass. Landsat data also contains the information of SWIR (short wave infrared), which supports the detection of vegetation sensitivity, so it is worthwhile adding SWIR data into the estimation models in further study.

5.3. Linking Forest Canopy Height to Biomass

In this study, the forest aboveground biomass was calculated through a power equation that is associated with canopy height. The evaluation result (R² = 0.70, RMSE = 35.81 Mg/ha, MRE = 17.0%) proved the equation to be reliable when producing a biomass map in Maryland. Our biomass estimation formula agreed well with previous studies [50,86]. However, the CMS maps error, as described in Section 2.3, will reduce the accuracy of our model. Apart from the forest canopy height, the forest aboveground biomass also maintained a close relationship with the DBH [9]. We can improve the accuracy by adding other remote sensing parameters that are related to DBH, such as LAI in future research.

5.4. Future Development

The GLAS instrument offers an unprecedented opportunity to estimate canopy height and biomass without field-measured trees metrics. Even though its principal objective was to measure ice sheet elevation change and sea ice thickness, the GLAS products were also widely applied to monitor land and vegetation. In this article, we only focused on only the vegetation within Maryland where the forest is relatively homogeneous. In future studies, an improved method will be put forward to compute the forest biomass at the continental or even global scales. Fortunately, NASA is planning to launch ICESat-2 and GEDI in 2018, and ESA will launch BIOMASS in 2020. With these data, researchers will have free access to the latest valuable data for assessing terrestrial forest changes.

6. Conclusions

This study demonstrated that the combination of the GLAS waveform and Landsat imagery could be used to monitor the forest aboveground biomass in Maryland. The total forest aboveground biomass in Maryland reached approximately 160 Tg. As the GLAS and Landsat data both covered the global surface, this method has the potential to evaluate forest resources at a larger scale. In this study, we conducted four different methods to estimate forest biomass and compared their performances. From the distribution of the estimates, machine learning models perform better than the first principal component power model, which produced canopy height concentrated in 20-40m and showed few local variations. However, machine learning models require significant additional costs in terms of time, effort, and computational resources.