Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure
Abstract
:1. Introduction
- to demonstrate the potential of TLS to detect changes in the vertical structure of the forest before and after liana removal
- to study the reproducibility of the TLS-derived metrics by comparing the structural metrics from two time steps of the control plot.
2. Materials and Methods
2.1. Study Site
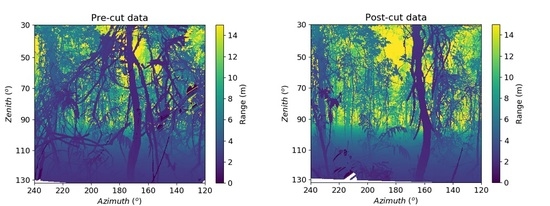
2.2. Experimental Set-Up
2.3. LiDAR Data
2.4. Co-Registration of Bi-Temporal Data
2.5. Vertical Plant Profiles
2.6. Nearest Neighbor Distance
2.7. Canopy Height Models
3. Results and Discussion
3.1. Vertical Plant Profiles
3.2. Nearest Neighbor Distance
3.3. Canopy Height Models
3.4. Limitations of the Study
4. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| TLS | Terrestrial Laser Scanning |
| DBH | Diameter at Breast Height |
| PAI | Plant Area Index |
| LAI | Leaf Area Index |
| PAVD | Plant Area Volume Density |
| CHM | Canopy Height Model |
| LiDAR | Light Detection and Ranging |
| PCL | Portable Canopy LiDAR |
| COI | Crown Occupancy Index |
| BCI | Barro Colorado Island |
| BCNM | Barro Colorado Natural Monunment |
| SPD | Sorted Pulse Data |
| ICP | Iterative Closest Point |
| KS | Kolmogorov–Smirnov |
| ANN | Average Nearest Neighbor |
Appendix A
Appendix A.1. Vertical Profiles of Pgap, PAI and PAVD

Appendix A.2. Co-Registration of the Bi-Temporal Scans
- We isolated the ground points from the TLS data of two time steps for both the removal and control plot using the Cloth Simulation Filter (CSF) algorithm implemented in CloudCompare. CSF is a tool to extract ground points from a discrete return LiDAR data [52].
- We derived stem maps from TLS for the two time steps following the method mentioned in Section 2.7.
- We used the stem points plus the ground points from these two pieces of different temporal data as input for the first coarse manual registration in CloudCompare with one point cloud as reference and the other as the one to be aligned.
- We then applied the transformation matrix from the manual registration to the whole point cloud to be aligned.
- We used the ICP algorithm [53] implemented in CloudCompare for fine registration after the first coarse manual registration. We selected all the points from the ground up to 4 m for fine registration.
- We applied the transformation matrix that resulted from the ICP fine registration to the whole point cloud to be aligned.

Appendix A.3. Additional Results

References
- Crowley, T.J. Causes of climate change over the past 1000 years. Science 2000, 289, 270–277. [Google Scholar] [CrossRef] [PubMed]
- Woods, P. Effects of logging, drought, and fire on structure and composition of tropical forests in Sabah, Malaysia. Biotropica 1989, 21, 290–298. [Google Scholar] [CrossRef]
- Wright, S.J. Tropical forests in a changing environment. Trends Ecol. Evol. 2005, 20, 553–560. [Google Scholar] [CrossRef] [PubMed]
- Schnitzer, S.A.; Bongers, F. Increasing liana abundance and biomass in tropical forests: Emerging patterns and putative mechanisms. Ecol. Lett. 2011, 14, 397–406. [Google Scholar] [CrossRef] [PubMed]
- Schnitzer, S.A.; Bongers, F. The ecology of lianas and their role in forests. Trends Ecol. Evol. 2002, 17, 223–230. [Google Scholar] [CrossRef]
- Rodríguez-Ronderos, M.E.; Bohrer, G.; Sanchez-Azofeifa, A.; Powers, J.S.; Schnitzer, S.A. Contribution of lianas to plant area index and canopy structure in a Panamanian forest. Ecology 2016, 97, 3271–3277. [Google Scholar] [CrossRef] [PubMed]
- Muthumperumal, C.; Parthasarathy, N. Diversity, distribution and resource values of woody climbers in tropical forests of southern Eastern Ghats, India. J. For. Res. 2013, 24, 365–374. [Google Scholar] [CrossRef]
- Bongers, F.; Schnitzer, S.; Traore, D. The importance of lianas and consequences for forest management in West Africa. BioTerre. 2002. Available online: https://www.researchgate.net/profile/Frans_Bongers/publication/40797530_The_importance_of_lianas_and_consequences_for_forest_management_in_West_Africa/links/0c960529614f4e6557000000.pdf (accessed on 22 March 2018).
- Hegarty, E.E. Distribution and abundance of vines in forest communities. Biol. Vines 1991, 313–334. [Google Scholar]
- Schnitzer, S.A.; Carson, W.P. Treefall gaps and the maintenance of species diversity in a tropical forest. Ecology 2001, 82, 913–919. [Google Scholar] [CrossRef]
- Vidal, E.; Johns, J.; Gerwing, J.J.; Barreto, P.; Uhl, C. Vine management for reduced-impact logging in eastern Amazonia. For. Ecol. Manag. 1997, 98, 105–114. [Google Scholar] [CrossRef]
- Putz, F.E. The natural history of lianas on Barro Colorado Island, Panama. Ecology 1984, 65, 1713–1724. [Google Scholar] [CrossRef]
- Appanah, S.; Putz, F. Climber abundance in virgin dipterocarp forest and the effect of pre-felling climber cutting on logging damage [Peninsular Malaysia]. Malays. For. 1984, 47, 335–342. [Google Scholar]
- Schnitzer, S.A.; Parren, M.P.; Bongers, F. Recruitment of lianas into logging gaps and the effects of pre-harvest climber cutting in a lowland forest in Cameroon. For. Ecol. Manag. 2004, 190, 87–98. [Google Scholar] [CrossRef]
- Pérez-Salicrup, D.R. Effect of liana cutting on tree regeneration in a liana forest in Amazonian Bolivia. Ecology 2001, 82, 389–396. [Google Scholar] [CrossRef]
- Gerwing, J.J. Testing liana cutting and controlled burning as silvicultural treatments for a logged forest in the eastern Amazon. J. Appl. Ecol. 2001, 38, 1264–1276. [Google Scholar] [CrossRef]
- Marshall, A.R.; Coates, M.A.; Archer, J.; Kivambe, E.; Mnendendo, H.; Mtoka, S.; Mwakisoma, R.; Figueiredo, R.J.; Njilima, F.M. Liana cutting for restoring tropical forests: A rare palaeotropical trial. Afr. J. Ecol. 2017, 55, 282–297. [Google Scholar] [CrossRef] [Green Version]
- Reid, J.P.; Schnitzer, S.A.; Powers, J.S. Short and long-term soil moisture effects of liana removal in a seasonally moist tropical forest. PLoS ONE 2015, 10, e0141891. [Google Scholar] [CrossRef] [PubMed]
- Van Der Heijden, G.M.; Powers, J.S.; Schnitzer, S.A. Lianas reduce carbon accumulation and storage in tropical forests. Proc. Natl. Acad. Sci. USA 2015, 112, 13267–13271. [Google Scholar] [CrossRef] [PubMed]
- Hancock, S.; Essery, R.; Reid, T.; Carle, J.; Baxter, R.; Rutter, N.; Huntley, B. Characterising forest gap fraction with terrestrial lidar and photography: An examination of relative limitations. Agric. For. Meteorol. 2014, 189, 105–114. [Google Scholar] [CrossRef] [Green Version]
- Calders, K.; Origo, N.; Disney, M.; Nightingale, J.; Woodgate, W.; Armston, J.; Lewis, P. Variability and bias in active and passive ground-based measurements of effective plant, wood and leaf area index. Agric. For. Meteorol. 2018, 252, 231–240. [Google Scholar] [CrossRef]
- Danson, F.M.; Hetherington, D.; Morsdorf, F.; Koetz, B.; Allgower, B. Forest canopy gap fraction from terrestrial laser scanning. IEEE Geosci. Remote Sens. Lett. 2007, 4, 157–160. [Google Scholar] [CrossRef] [Green Version]
- Jupp, D.L.; Culvenor, D.; Lovell, J.; Newnham, G.; Strahler, A.; Woodcock, C. Estimating forest LAI profiles and structural parameters using a ground-based laser called ‘Echidna®. Tree Physiol. 2009, 29, 171–181. [Google Scholar] [CrossRef] [PubMed]
- Calders, K.; Armston, J.; Newnham, G.; Herold, M.; Goodwin, N. Implications of sensor configuration and topography on vertical plant profiles derived from terrestrial LiDAR. Agric. For. Meteorol. 2014, 194, 104–117. [Google Scholar] [CrossRef]
- Yang, X.; Strahler, A.H.; Schaaf, C.B.; Jupp, D.L.; Yao, T.; Zhao, F.; Wang, Z.; Culvenor, D.S.; Newnham, G.J.; Lovell, J.L.; et al. Three-dimensional forest reconstruction and structural parameter retrievals using a terrestrial full-waveform lidar instrument (Echidna®). Remote Sens. Environ. 2013, 135, 36–51. [Google Scholar] [CrossRef]
- Liang, X.; Litkey, P.; Hyyppa, J.; Kaartinen, H.; Vastaranta, M.; Holopainen, M. Automatic stem mapping using single-scan terrestrial laser scanning. IEEE Trans. Geosci. Remote Sens. 2012, 50, 661–670. [Google Scholar] [CrossRef]
- Calders, K.; Schenkels, T.; Bartholomeus, H.; Armston, J.; Verbesselt, J.; Herold, M. Monitoring spring phenology with high temporal resolution terrestrial LiDAR measurements. Agric. For. Meteorol. 2015, 203, 158–168. [Google Scholar] [CrossRef]
- Srinivasan, S.; Popescu, S.C.; Eriksson, M.; Sheridan, R.D.; Ku, N.W. Multi-temporal terrestrial laser scanning for modeling tree biomass change. For. Ecol. Manag. 2014, 318, 304–317. [Google Scholar] [CrossRef]
- Liang, X.; Hyyppä, J.; Kaartinen, H.; Holopainen, M.; Melkas, T. Detecting changes in forest structure over time with bi-temporal terrestrial laser scanning data. ISPRS Int. J. Geo-Inf. 2012, 1, 242–255. [Google Scholar] [CrossRef]
- Olivier, M.D.; Robert, S.; Fournier, R.A. A method to quantify canopy changes using multi-temporal terrestrial lidar data: Tree response to surrounding gaps. Agric. For. Meteorol. 2017, 237, 184–195. [Google Scholar] [CrossRef]
- Parker, G.G.; Harding, D.J.; Berger, M.L. A portable LIDAR system for rapid determination of forest canopy structure. J. Appl. Ecol. 2004, 41, 755–767. [Google Scholar] [CrossRef]
- Sánchez-Azofeifa, A.; Portillo-Quintero, C.; Durán, S. Structural effects of liana presence in secondary tropical dry forests using ground LiDAR. Biogeosci. Discuss. 2015, 12, 17153–17175. [Google Scholar] [CrossRef]
- Sánchez-Azofeifa, G.A.; Guzmán-Quesada, J.A.; Vega-Araya, M.; Campos-Vargas, C.; Durán, S.M.; D’Souza, N.; Gianoli, T.; Portillo-Quintero, C.; Sharp, I. Can terrestrial laser scanners (TLSs) and hemispherical photographs predict tropical dry forest succession with liana abundance? Biogeosciences 2017, 14, 977. [Google Scholar] [CrossRef]
- Schnitzer, S.A.; Kuzee, M.E.; Bongers, F. Disentangling above-and below-ground competition between lianas and trees in a tropical forest. J. Ecol. 2005, 93, 1115–1125. [Google Scholar] [CrossRef]
- Schnitzer, S.A.; Rutishauser, S.; Aguilar, S. Supplemental protocol for liana censuses. For. Ecol. Manag. 2008, 255, 1044–1049. [Google Scholar] [CrossRef]
- Bunting, P.; Armston, J.; Lucas, R.M.; Clewley, D. Sorted pulse data (SPD) library. Part I: A generic file format for LiDAR data from pulsed laser systems in terrestrial environments. Comput. Geosci. 2013, 56, 197–206. [Google Scholar] [CrossRef]
- Bunting, P.; Armston, J.; Clewley, D.; Lucas, R.M. Sorted pulse data (SPD) library—Part II: A processing framework for LiDAR data from pulsed laser systems in terrestrial environments. Comput. Geosci. 2013, 56, 207–215. [Google Scholar] [CrossRef]
- Girardeau-Montaut, D. Cloudcompare-Open Source Project. OpenSource Project. 2011. Available online: http://www.danielgm.net/cc/ (accessed on 14 November 2016).
- Massey, F.J., Jr. The Kolmogorov-Smirnov test for goodness of fit. J. Am. Stat. Assoc. 1951, 46, 68–78. [Google Scholar] [CrossRef]
- Burt, A.; Disney, M.; Calders, K. Extracting individual trees from lidar point clouds using treeseg. Methods Ecol. Evol. 2018. in review. [Google Scholar]
- Popescu, S.C.; Wynne, R.H.; Nelson, R.F. Measuring individual tree crown diameter with lidar and assessing its influence on estimating forest volume and biomass. Can. J. Remote Sens. 2003, 29, 564–577. [Google Scholar] [CrossRef]
- Krooks, A.; Kaasalainen, S.; Kankare, V.; Joensuu, M.; Raumonen, P.; Kaasalainen, M. Predicting tree structure from tree height using terrestrial laser scanning and quantitative structure models. Silva Fenn 2014, 48, 1125. [Google Scholar] [CrossRef]
- Larjavaara, M.; Muller-Landau, H.C. Measuring tree height: A quantitative comparison of two common field methods in a moist tropical forest. Methods Ecol. Evol. 2013, 4, 793–801. [Google Scholar] [CrossRef]
- Maas, H.G.; Bienert, A.; Scheller, S.; Keane, E. Automatic forest inventory parameter determination from terrestrial laser scanner data. Int. J. Remote Sens. 2008, 29, 1579–1593. [Google Scholar] [CrossRef]
- Calders, K.; Newnham, G.; Burt, A.; Murphy, S.; Raumonen, P.; Herold, M.; Culvenor, D.; Avitabile, V.; Disney, M.; Armston, J.; et al. Nondestructive estimates of above-ground biomass using terrestrial laser scanning. Methods Ecol. Evol. 2015, 6, 198–208. [Google Scholar] [CrossRef]
- Fournier, R.A.; Côté, J.F.; Bourge, F.; Durrieu, S.; Piboule, A.; Béland, M. A method addressing signal occlusion by scene objects to quantify the 3D distribution of forest components from terrestrial lidar. In Proceedings of the SilviLaser 2015, La Grande Motte, France, 28–30 September 2015; pp. 29–31. [Google Scholar]
- Hancock, S.; Anderson, K.; Disney, M.; Gaston, K.J. Measurement of fine-spatial-resolution 3D vegetation structure with airborne waveform lidar: Calibration and validation with voxelised terrestrial lidar. Remote Sens. Environ. 2017, 188, 37–50. [Google Scholar] [CrossRef]
- Clark, D.B.; Clark, D.A. Distribution and effects on tree growth of lianas and woody hemiepiphytes in a Costa Rican tropical wet forest. J. Trop. Ecol. 1990, 6, 321–331. [Google Scholar] [CrossRef]
- Avalos, G.; Mulkey, S.S.; Kitajima, K.; Wright, S.J. Colonization strategies of two liana species in a tropical dry forest canopy. Biotropica 2007, 39, 393–399. [Google Scholar] [CrossRef]
- Tobin, M.F.; Wright, A.J.; Mangan, S.A.; Schnitzer, S.A. Lianas have a greater competitive effect than trees of similar biomass on tropical canopy trees. Ecosphere 2012, 3, 1–11. [Google Scholar] [CrossRef]
- Wilkes, P.; Lau, A.; Disney, M.; Calders, K.; Burt, A.; de Tanago, J.G.; Bartholomeus, H.; Brede, B.; Herold, M. Data acquisition considerations for Terrestrial Laser Scanning of forest plots. Remote Sens. Environ. 2017, 196, 140–153. [Google Scholar] [CrossRef]
- Zhang, W.; Qi, J.; Wan, P.; Wang, H.; Xie, D.; Wang, X.; Yan, G. An easy-to-use airborne LiDAR data filtering method based on cloth simulation. Remote Sens. 2016, 8, 501. [Google Scholar] [CrossRef]
- Besl, P.J.; McKay, N.D. Method for registration of 3-D shapes. In Sensor Fusion IV: Control Paradigms and Data Structures; International Society for Optics and Photonics: Bellingham, WA, USA, 1992; Volume 1611, pp. 586–607. [Google Scholar]












| Plot Type | Tree No. | Diameter at Breast Height (cm) | Height (m) | No. of Liana Stems on the Tree | Basal Area of Liana Load (cm2) |
|---|---|---|---|---|---|
| Removal Plot | 1 | 10.9 | 12.3 | 5 | 9.09 |
| 2 | 16.1 | 15.3 | 18 | 60.83 | |
| 3 | 12.6 | 13.3 | |||
| 4 | 43.7 | 25.2 | 10 | 83.13 | |
| 5 | 15.3 | 14.9 | 18 | 96.29 | |
| Control Plot | 1 | 47.4 | 26.1 | - | - |
| 2 | 11.7 | 12.8 | - | - | |
| 3 | 21.2 | 17.7 | - | - | |
| 4 | 15.5 | 14.9 | - | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Krishna Moorthy, S.M.; Calders, K.; Di Porcia e Brugnera, M.; Schnitzer, S.A.; Verbeeck, H. Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure. Remote Sens. 2018, 10, 810. https://doi.org/10.3390/rs10060810
Krishna Moorthy SM, Calders K, Di Porcia e Brugnera M, Schnitzer SA, Verbeeck H. Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure. Remote Sensing. 2018; 10(6):810. https://doi.org/10.3390/rs10060810
Chicago/Turabian StyleKrishna Moorthy, Sruthi M., Kim Calders, Manfredo Di Porcia e Brugnera, Stefan A. Schnitzer, and Hans Verbeeck. 2018. "Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure" Remote Sensing 10, no. 6: 810. https://doi.org/10.3390/rs10060810
APA StyleKrishna Moorthy, S. M., Calders, K., Di Porcia e Brugnera, M., Schnitzer, S. A., & Verbeeck, H. (2018). Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure. Remote Sensing, 10(6), 810. https://doi.org/10.3390/rs10060810