Next Article in Journal
Cloud Classification in Wide-Swath Passive Sensor Images Aided by Narrow-Swath Active Sensor Data
Next Article in Special Issue
Hydrologic Evaluation of Multi-Source Satellite Precipitation Products for the Upper Huaihe River Basin, China
Previous Article in Journal
Terrestrial Laser Scanning to Detect Liana Impact on Forest Structure
Previous Article in Special Issue
Decorrelation of Satellite Precipitation Estimates in Space and Time
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 10
Issue 6
10.3390/rs10060811
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Rain Microstructure Parameters Vary with Large-Scale Weather Conditions in Lausanne, Switzerland

by
Wael Ghada
1,*,
Allan Buras
1,
Marvin Lüpke
1,
Christian Schunk
1 and
Annette Menzel
1,2
1
Department of Ecology and Ecosystem Management, Technical University of Munich, Hans-Carl-von-Carlowitz-Platz 2, D-85354 Freising, Germany
2
Institute for Advanced Study, Technical University of Munich, Lichtenbergstraße 2a, D-85748 Garching, Germany
*
Author to whom correspondence should be addressed.
Remote Sens. 2018, 10(6), 811; https://doi.org/10.3390/rs10060811
Submission received: 9 April 2018 / Revised: 12 May 2018 / Accepted: 22 May 2018 / Published: 23 May 2018
(This article belongs to the Special Issue Remote Sensing of Precipitation)
Browse Figures
Versions Notes

Abstract

:
Rain properties vary spatially and temporally for several reasons. In particular, rain types (convective and stratiform) affect the rain drop size distribution (DSD). It has also been established that local weather conditions are influenced by large-scale circulations. However, the effect of these circulations on rain microstructures has not been sufficiently addressed. Based on DSD measurements from 16 disdrometers located in Lausanne, Switzerland, we present evidence that rain DSD differs among general weather patterns (GWLs). GWLs were successfully linked to significant variations in the rain microstructure characterized by the most important rain properties: rain intensity (R), mass weighted rain drop diameter (Dm), and rain drop concentration (N), as well as Z = ARb parameters. Our results highlight the potential to improve radar-based estimations of rain intensity, which is crucial for several hydrological and environmental applications.

Graphical Abstract

1. Introduction

Ground measurements of the rain drop size distribution (DSD) have attracted scientists’ attention for a variety of reasons. (1) Variations in the rain DSD influence the relationship between the radar reflectivity factor (Z) and the rainfall intensity (R) [1]. An accurate estimation of R is essential for important applications in hydrology, water management, and flood protection; (2) Rain kinetic energy depends on rain DSD and influences soil erosion in different scales [2,3]; (3) Rain drops have the potential to wash particulate pollutants off impermeable surfaces, affecting the ecology of urban waterways [4]; (4) Rainfall distorts telecommunication signals and radio propagation, especially at high frequencies [5], all of which are influenced by rain DSD [6]; (5) Specific methods used to separate rain type (convective and stratiform) are based on rain DSD [7,8]. Consequently, different tools and methods have been developed to detect rain DSD and to improve our understanding of its underlying processes.
Automated disdrometers measure rain DSD on the ground with high temporal resolution. These measurements are used to detect variations in the rain DSD on different temporal and local scales. Rain DSD parameters may vary at a scale of a few meters, and the small sampling areas of disdrometers contribute to this variation [9]. The rain DSD also varies within the area of one weather radar pixel (1 km2) [10]. The detected spatial variation increases with the increasing distance between disdrometers [11]. It exists even when decreasing the temporal resolution [12]. DSD parameter variation has also been confirmed on regional [13] and global [14] scales. Seasonality, rain type, climate regime, and their combinations also result in different rain DSD [15,16,17]. The rain DSD even differs from event to event [18].
Rain DSD variation is linked to the microphysical processes of rain formation such as coalescence [19], fragmentation [19,20], evaporation [19,21,22], and size sorting of rain drops by wind drafts [23]. Also conditions such as the height of freezing levels, the boundary layer relative humidity [24], and aerosols’ abundance and properties [25,26] influence rain DSD.
Rain DSD evolves under the complex micro- and mesoscale conditions. For example, topography influences the interaction between rain forming processes in orographic rain [27,28,29]. In addition, rain DSD varies within the stages of squall lines [16,30]. It also varies in convective versus stratiform rain, continental versus maritime rain, and warm versus cold rain [24,31,32]. Munchak et al. [24] explained that convective rain is associated with strong updrafts where cloud tops are above the freezing level, and both warm and cold rain forming processes occur. In contrast, updraft in stratiform rain is limited, and cold processes prevail. Rain DSD observations confirm the distinct microstructure between both rain types, with larger drops and higher intensities in convective rain [8,13,33,34]. Since they are based on prevailing flow directions and source regions of air masses govern several of the aforementioned influencing factors at the local scale, we hypothesize that large scale weather conditions may help to improve our knowledge about and thus modeling of parameters related to rain DSD.
Weather type classification has proven to be useful in understanding climatic processes and the link between the variability of local weather conditions and atmospheric circulations [35,36]. Weather types represent the atmospheric conditions that prevail over a large area and remain relatively stable for several days (a minimum of three days) [37]. These atmospheric conditions include the location of sea-level, semi-permanent pressure centers, the position and paths of frontal zones and the existence of cyclonic or anticyclonic circulation types [38]. Methods have been developed and used to classify weather types into patterns and groups [35]. In this paper, the classification of weather types by Hess and Brezowsky [39] is used. Their classes are called general weather patterns and are abbreviated as GWL, which is derived from the German word “Großwetterlage.” In this classification, each day is assigned to one of 29 GWL classes or a transitional type, and each GWL lasts three days or more [40]. The relationship between large-scale weather types and local weather phenomena has been verified previously, e.g., some weather types have a major influence on the generation of extremely hot days [41]. Moreover, GWLs influence stream flows [42], floods [43,44], forest fires [45], and even debris-flow events [46]. More directly, GWLs have a substantial influence on precipitation totals, particularly on their extreme values [47,48,49] and even seasonal extremes [50]. Consequently, because changes in weather type frequencies relate to changes in precipitation amounts and extremes [51], a better understanding of the impact of large-scale circulations on intense (sub-)daily precipitation is required [52].
Synoptic weather types provide a combination of meteorological factors that influence the rain DSD. Fernandez-Raga et al. [53] provided convincing evidence that weather patterns with northern components are associated with smaller rain drops in Leon, Spain. On the other hand, western and southwestern components carry humidity from the Atlantic and have larger drops. Hachani et al. [29] verified the different rain DSD characteristics and Z–R relationship between different factors including weather patterns, seasons, location, and rain fall type in the Cévennes–Vivarais region, France. They also investigated the combined effects of weather patterns and locations. However, the combined effect of rain type and weather patterns on the rain DSD has not yet been addressed.
Based on these outlined knowledge gaps, we address two general questions here.
(I)
Does the rain microstructure differ between general weather patterns in both convective and stratiform rain types?
(II)
How much does this influence the radar reflectivity and rain rate, i.e., the Z–R relation?

2. Materials and Methods

2.1. Data Sources

We based our analyses on a published dataset collected by 16 “OTT PARSIVEL” disdrometers spanning the period from December 2008 through September 2010 in Lausanne, Switzerland (the EPFL-LTE campaign) [54]. The disdrometers were deployed over an area of less than 1 km2. The aim of the original campaign was to assess the spatial variability within the area covered by one pixel of weather radar. The dataset has temporal resolutions of 20 s and 30 s. A detailed map of the disdrometers locations, a description of the campaign, data structure, and the measured parameters is given in Jaffrain et al. [10,11]. For the purpose of this paper, when comparing properties between GWLs, all the intervals were aggregated to a one-minute temporal resolution. Each minute interval measured by a device was considered to be a realization of the rain properties of the associated GWL, which means that up to 16 simultaneous realizations of rain properties were available for each minute of rain. It is important to note that the 16 disdrometers were not deployed at the same time, and not all of them measured for the entire 22-month period. This resulted in variations in the total rain duration and amount measured across the devices. The accumulated rain amount and duration measured by each device along with the start and end dates of the measurements are provided in Table S1.
There was also a difference between the total mean amount of rain recorded over the network that is reported in the published dataset (1275 mm) [54] and the total mean reported in our analysis (1027 mm). This is a result of the filtering procedures, which are explained in Section 2.5.
The German Meteorological Service (DWD) performs a daily classification of the general weather patterns. This classification is based on Hess and Brezowsky [39] and includes 29 GWL classes and 1 transitional class. The daily records of this classification are published online [55,56,57]. The 29 GWLs can be aggregated according to the patterns of the air parcel movements (zonal, meridional, or mixed), the rotation direction (cyclonic or anti-cyclonic), and the flow direction. Table 1 lists all the GWLs and the corresponding five major classes of flow directions [50]. Each GWL is associated to one of these five classes, which indicates the origin of the moving air parcels, as derived from the wind flow direction at upper levels (500 hPa). These five classes are referred to as the flow directions throughout the text.

2.2. Measurement Device

The “OTT PARSIVEL” disdrometer is an optical, laser-based device that measures the size and velocity of hydrometeors. It counts the number of hydrometeors that fall in 32 diameter ranges and 32 velocity ranges. The first two diameter ranges are not used by the disdrometer and are always empty leaving an actual detection range of 0.31–24.5 mm. The 32 velocity ranges extend from 0.05 m·s−1 to 20.8 m·s−1. A list of the diameter ranges is available in [58]. The disdrometer uses a horizontal laser sheet with a detection area of 54 cm2 (180 mm × 30 mm). Whenever a hydrometeor passes through this sheet, the laser signal is reduced and the diameter is calculated according to this reduction. The velocity is derived from the size of the hydrometeor and the time it takes to pass the laser detection sheet. In addition, OTT PARSIVEL disdrometers provide an automated separation for the precipitation type based on the combination of the size and velocity values in each interval. A more detailed description of the OTT PARSIVEL device is provided by Löffler-Mang and Joss [59].
The disdrometer raw output was used in this study to obtain the values of the rain intensity R [mm·h−1], reflectivity Z [mm6·m−3 and d B Z ], total drop concentration N [m−3], and mass weighted diameter Dm [mm]. Equations (A1)–(A5) [16,60,61] were used to obtain these values (Appendix A). The parameters, R, Dm, and N, best illustrate the distinct physical rain properties for both rain types.

2.3. Separation of Convective and Stratiform Rain Intervals

Several methods to separate convective and stratiform rain are available in the literature. These methods are based on instrumental data, e.g., from radar and wind profilers. Some methods have also suggested the use of rain DSD parameters [7,8]. Here the separation of convective and stratiform rain intervals follows the simple procedure proposed by Bringi et al. [15], which has already been adopted in several studies [18,62]. Rain is regarded as convective if R is larger than 10 mm·h−1 or if the standard deviation of the rain intensities over five consecutive two-minute intervals is larger than 1.5 mm·h−1; otherwise, the rain interval is considered to be stratiform.

2.4. Data Filtering

Error sources and shortcomings of disdrometers in general and OTT PARSIVEL disdrometers in particular include: wind effects, unstable laser source, splashing effect, drops falling through the edges of the detection area (margin fallers), non-rain particles such as insects and flying seeds, drops falling simultaneously through the device detection area (masking effect), and the small sampling area [9,63,64]. To minimize these errors, we adopted the procedure suggested and explained in detail by Friedrich et al. [64], composed of the following steps in the presented order.
  • Intervals characterized by high wind speed were completely removed from the dataset. These intervals were indicated by the existence of large drops D > 5 mm with a low falling speed V < 1 m·s−1.
  • All particles larger than 8 mm in diameter were not considered to be rain and filtered out.
  • Particles with velocities higher than 160% of the associated terminal velocity for the diameter class center as given by Atlas et al. [65] were filtered out (margin fallers).
  • Small particles (D < 2 mm) with low velocity (<40% of the terminal velocity) were filtered out (splashing).
  • Large particles (D > 5 mm) with low velocity (<40% of the terminal velocity) were filtered out (hail).
  • For particles with a diameter between 2 mm and 5 mm, a fall velocity threshold was established based on the average terminal velocity of rain and graupel for each diameter bin. Then, all particles with a fall velocity below this threshold were filtered out.
In addition, we excluded:
  • Intervals associated with a damaged laser signal as reported in the raw output of the disdrometers;
  • Intervals associated with snow, hail, frozen rain, or mixed precipitation as reported by the disdrometer;
  • Intervals with rain intensities lower than 0.1 mm·h−1;
  • Intervals where three or less diameter bins recorded rain drops to ensure the existence of a drop size distribution; and
  • Intervals of rain that occurred in the transitional GWL U.
In total, the dataset was composed of rain DSD records in 25 GWLs, after excluding the transitional GWL U, and four other GWLs for which no rain was recorded (Table 1). These 25 GWLs form the base of the results in Section 3.1. However, when discriminating the rain type into convective and stratiform, the inhomogeneous frequency of GWLs, as well as the variation in the rain duration and rain amount per GWL, resulted in a varying number of rain intervals detected for each GWL–rain type combination. Some GWLs had only a small number of rain intervals per rain type. Therefore, to compare the rain microstructure (Section 3.2) and the Z–R parameters (Section 3.3), GWLs that had less than 500 min of accumulated convective duration or 1000 min of accumulated stratiform rain over all 16 devices (shaded cells in Table 1) were excluded from the analysis in these sections. This reduced the number of GWLs to 20 for stratiform rain and 16 for convective rain. The lower threshold in the case of convective rain was based on the generally lower duration of detected convective rain per GWL.

2.5. Assessing the Performance of the Z–R Relation

Rain intensity R [mm·h−1] retrieval from weather radars is generally based on the Z relation:
Z = A × R b ,
where Z [mm6·m−3] is usually measured directly by the weather radar, while A and b are determined for each rain type separately. Then, Equation (1) is used to determine R. Here, conversely, the values of R and Z were calculated for each interval from the raw output of the disdrometers, as explained in Appendix A. Then, a linear regression of log(Z) and R was used to determine the values of A and b using two models. The general Z–R model takes only rain type into account, resulting in one value of A and one value of b for each rain type, convective and stratiform. In the GWL Z–R model, A and b are specifically determined for each combination of GWL and rain type.
To evaluate the performance of the two models, the mean absolute error (MAE) of the rain intensity (R) estimations of each model was used as recommended by Willmott and Matsuura [66]. The R values based on Equation (A1) were considered to be the accurate observed values, while the model outputs of R were considered to be the prediction. MAE is given by
  MAE = n − 1 ∑ 1 n | e i | ,
where n is the number of observations, e i is the model prediction error: e i = V m i − V o i , V m i is the model prediction value, V o i is the observed value, and i is the observation index.
The relative error was also used to assess the overestimation (or underestimation) of the total rain amount by both models for the entire dataset, as well as for each GWL-rain type combination:
  RE = ∑ e i / ∑ V o i .
To obtain a robust evaluation of both models, we separated the dataset into a training subset (2/3 of the rain intervals in each GWL/rain type combination chosen randomly) and a testing subset (the remaining 1/3 of the dataset). Both models were built based on the training subset, then evaluated by calculating MAE and RE from the testing subset. The whole process was repeated 100 times and the reported values in Section 3.3 represent the mean of these repetitions.
The 16 disdrometers were deployed within 1 km2, which allows comparisons of the spatial variation of A and b at this scale versus their GWL-specific variations. Therefore, the A and b values were determined for each device-rain type combination and then were compared with the A and b values of the GWL Z–R model.

2.6. Statistical Tests

For the parameters R, Dm, and N, a normality check was performed by means of visual inspections (QQ plots and histograms) and a Shapiro–Wilk normality test. Because all parameters were non-normally distributed (p-value of Shapiro–Wilk test < 0.05), non-parametric tests were chosen. To compare more than two groups, the Kruskal–Wallis test was performed to detect the existence of significantly different parameters (p-value < 0.05) between GWLs and a pairwise Wilcoxon test was performed to check the significance of the differences between each pair of GWLs. These steps were performed for each rain type separately. A similar procedure was followed when comparing these parameters between flow directions (cf. Table 1).
To compare the spatial variability of the Z–R parameters (A and b) against their GWL variability, the A and b values were calculated for each device and then for each GWL. A normality check was performed for the A and b values. An F-test was used for the normally distributed parameters (only A in the case of stratiform rain), and Levene’s test was used for the non-normally distributed parameters. The normality check and the variance comparisons were performed separately for each rain type.
Data filtering, analyses, and plots were performed using the statistical computing environment R [67], the integrated development environment RStudio [68], and the data visualization package ggplot2 [69].

3. Results

3.1. Variation in Rain Duration, Amount and Rates with Rain Type and GWL

This section provides an overview of the rain records in general and within each rain type and GWL. We aim at demonstrating the variation in convective rain proportions between GWLs, which emphasizes the importance of separation by rain type for comparing rain microstructure among GWLs (see Section 4.2).
After filtering, a total of 598,665 one-minute DSD samples (42% of the total dataset) were included in the analyses. The total detected rain amount was 16,439 mm accumulated over the 16 disdrometers, with a median rain intensity of 0.79 mm·h−1 (standard deviation (sd): 3.37 mm·h−1). Convective rain covered on average only 11% of the detected rain duration (Figure 1a). However, the amount of rain in the convective intervals represented approximately 40% of the total detected rain (Figure 1b). This is due to the large difference in the rain intensities between the stratiform and convective rain (medians of 0.69 mm·h−1 (sd: 1.1 mm·h−1) and 4.49 mm·h−1 (sd: 8.5 mm·h−1), respectively) (Figure 1c).
In general, the proportions of the convective rain duration and the rain amount for convective and stratiform rain were similar for the 16 disdrometers, despite the differences in the accumulated rain durations and amounts detected by the 16 devices (as explained in Section 2.1).
However, the convective rain was not distributed evenly across GWLs; variations in the proportion of convective rain were detected both in the rain duration and the rain amount (Figure 2b,c). While some GWLs recorded higher than the average (11%) proportion of convective rain duration (e.g., HM, NZ, TRM, and TM), less than the average convective rain duration was measured in others (e.g., WS, NEZ, SEZ, and TRW) (Figure 2b). The variation between GWLs was higher regarding the rain amount (Figure 2c), with convective rain representing more than 65% of the rain amount for HM and NZ but 17% of WS and less than 2% for SEZ and HFZ.
Visual inspection of the convective rain proportions did not reveal differences between cyclonic and anticyclonic GWLs in duration or rain amount. Conversely, the flow direction revealed small convective rain duration proportions in the NE–E (6%) compared to higher percentages in the other flow directions, especially CE (17%) (Figure 3a). NE–E circulations were also associated with the smallest proportion of convective rain amount (31%) compared to the four other flow directions (37–51%) (Figure 3b). This was confirmed by comparing individual GWLs; the highest proportion of convective rain duration and amount occurred in HM, which belongs to GWLs with no specific flow direction CE, while no convective rain was recorded in some NE–E circulations such as HFZ and NEA (Figure 2b,c).

3.2. Rain Microstructure

3.2.1. Drop Size Distribution (DSD)

GWL-specific rain DSDs differed from each other and from the overall mean rain DSD. This is illustrated for both rain types by comparing the mean rain concentrations for each 1 mm of the diameter range (Figure 4). To aid in the interpretation, the plot in Figure 4 contains a selection of GWLs that demonstrated a distinct DSD shape.
In the case of stratiform rain (Figure 4a), most GWL-averaged concentrations followed the overall average concentration shape and fell within ±400 drops around the average rain concentration per diameter range. The variance was larger near the peak concentration, which corresponds to a drop size of 0.69 mm, and became smaller as the rain drop diameter diverged from the peak. The highest peaks of the stratiform rain concentration were associated with the GWLs SWA, NZ, and TM. SEZ had the lowest peak. The concentration curve had a broader peak shifted to the left side (a high number of small drops) for HNFZ, while HFA was slightly shifted to the right and recorded the highest number of drops larger than 1.5 mm in diameter. These differences led to significant differences between GWLs when assessing the rain microstructure parameters (see Section 3.2.2).
In contrast to the pronounced peak in stratiform rain DSD, convective rain showed a wider range of high concentrations (0.69–0.94 mm) (Figure 4b). The curves for convective rain were shifted toward larger diameters with much higher rain drop concentrations. The variation in the concentration averages between GWLs was much larger in all diameter ranges reaching up to ±1000 drops near the peak. The highest peaks were associated with the GWLs WS, SWA, TM, and NZ, with TM having the highest concentration of drops smaller than 1.5 mm in diameter. GWLs with the lowest concentration peaks were HFA, BM, TB, and WW. WW, HM, and HFA had the highest number of drops larger than 1.5 mm in diameter.
Testud et al. [70] proposed the concept of normalized distribution to compare rain DSDs without presumptions about their shapes. The results of applying the method of normalized DSD are provided in Figures S1 and S2.

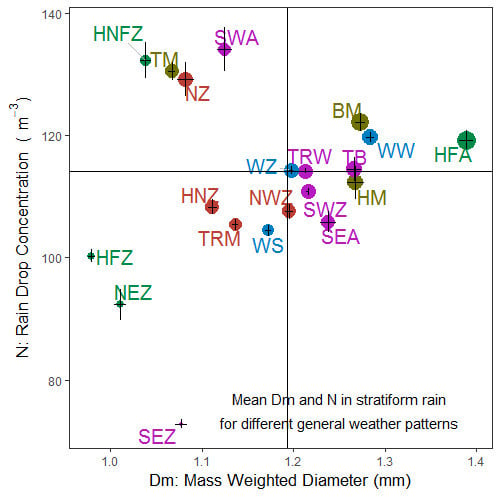
3.2.2. Rain Parameters R, Dm and N

While the differences between GWLs regarding the rain DSD appear to be small, the high number of drops per interval and the large number of intervals led to significant differences in the three main rain parameters. The following comparisons were made without discrimination between the different devices.
When analyzing the stratiform rain intervals, the average values of R, N, and Dm of the three most frequent GWLs (TRW, SWZ, and WZ) were very close to the overall averages of these parameters (Figure 5a). These three GWLs are typical Atlantic frontal systems associated with moderate temperatures and therefore average rain intensities. GWLs with high average R (HFA, BM, WW, TB, and HM) recorded the highest Dm values, while GWLs with the highest N averages were associated with close to average R values. Conversely, GWLs with the smallest R averages (SEZ, NEZ, and HFZ) had low values of both average Dm and N. GWLs that belong to the same flow direction (identical colors in Figure 5a) are clustered in the space of N and Dm, with the exception of some outliers (HFA, SEZ, and SWA).
The R, Dm, and N values of stratiform rain vary significantly between the five classes of flow direction (cf. Table 1) despite their considerable variance within each flow direction. NE–E GWLs had the smallest average value of R associated with the lowest average Dm (Figure 6). CE had the highest value of R with the highest value of N and a very high value of Dm. Both S and W had very high values of R and Dm.
For convective rain, the three parameters R, Dm, and N had larger values and variations among GWLs than those for stratiform rain (Figure 5b). The average R values ranged from 3.67 mm·h−1 for NWZ to 8.56 mm·h−1 for HFA. High average R values were associated with large drops (Dm) and vice versa, with the exception of two cases: (1) TM had the second highest average R despite having a very low Dm, while N was comparably large and (2) WW had a less than average R value despite having the highest average Dm due to a small average N. The most frequent GWLs in convective rain (SWZ, WZ, and TRW) had higher than average R values but close to average Dm values.
The R, Dm and N values also varied for different flow directions in convective rain (Figure 6b). NW–N GWLs had the smallest rain intensity despite having the largest average N values. The other four flow directions recorded higher values of both Dm and R. This pattern differs from the one demonstrated in stratiform rain, which might be an indication of a larger influence of local conditions in convective rain.

3.3. The Z–R Relation

Based on the global Z–R model for the entire dataset, A was estimated to be 295 for stratiform rain and 278 for convective rain. The values for b were 1.49 for stratiform rain and 1.54 for convective rain. For the GWL Z–R model, the A and b values differed between the individual GWLs in both rain types (Figure 7). Most A values for stratiform rain were clustered in the range of 215–350, while b values clustered in the range of 1.35–1.65, with the exception of SEZ, which had higher values for both A and b. Convective rain had a larger range for both A (189–371) and b (1.36–1.84) compared to stratiform rain (excluding the SEZ results).
The spatial variation of the A and b values from a selection of events in this dataset has been discussed in detail by Jaffrain and Berne [71]. In our case, comparable results were achieved by using the entire dataset to estimate the A and b values associated with each of the 16 devices. The variability of the A and b values was significantly larger for the GWL Z–R model compared to the spatial variability in both rain types (Figure 7).
The mean average error (MAE) in the rain rates indicated a better performance of the GWL model in comparison to the global model (Table 2).
Using the global model resulted in a 10.4% overestimation of the total detected rain amount, while using the GWL model resulted in an overestimation of 9.4%. The improvement resulting from using the GWL Z–R model was particularly high within some GWLs. For stratiform rain, the improvement reached 55%, 21%, and 11% for SEZ, WW, and HM, respectively. For convective rain, the improvement reached 92%, 47%, and 15% for WW, HM, and BM, respectively (Figure 8). These GWLs showed distinct averages of Dm and N, as illustrated in Figure 5.

4. Discussion

4.1. Weather Type Classification

The Hess–Brezowsky classification was chosen due to its availability even for a longer period, its proven suitability for Central Europe, and its basis on the surface and 500 hPa height pressure patterns with the latter being especially important for the formation of precipitation [47]. The Hess–Brezowsky circulation type records experienced a shift in frequencies in the mid-1980s and therefore should not be used for climatological analyses [72]. However, this is not a problem in our case because the dataset and the analyses were limited to a period shorter than two years, which does not fall within the mid-1980s.
Another concern is the influence of orographic rain on the proportion of convective rain per GWL and per flow direction. The chosen method is not able to distinguish orographic rain. However, we assume that the proportion of orographic rain within a specific GWL or flow direction would be stable for a given location. Seasonality also might influence the proportion of convective rain per GWL. Unfortunately, the dataset used does not allow for a proper analysis of likely seasonal variation.

4.2. Rain Type Classification

Separation of convective and stratiform rain by the described simple method of [15] is prone to misclassification. This method does not recognize intervals where both convective and stratiform rain occur [73,74]. In addition, the transition between convective and stratiform rain cannot be properly distinguished by using the five successive 2-min rain intensity records [74]. However, it was chosen because data necessary for other separation methods were not available (e.g., wind profilers or 2D video disdrometers [75,76]).
The proportion of the convective rain amount in this dataset (40%) falls within the range reported for Central Europe by Rulfová and Kyselý [76] (30–50%). A higher percentage of convective rain is reported for tropical areas: on average 52% and 45% for continental and oceanic convective rain, respectively [77]. Even higher levels (52–69%) are reached for different locations in India [13].
Stratiform rain was more frequent than convective rain in all GWLs. However, convective rain represented more than half the total rain amount in some GWL classes, while this percentage dropped to less than 2% for other classes. GWLs with no specific prevailing flow direction (CE) provided a higher probability of convective rain due to their low-pressure gradients. Most GWLs associated with clear flow directions had a smaller proportion of convective rain because frontal structures may prevail. Despite the limited measurement duration of some of the addressed weather patterns, our results indicate that some GWLs provide conditions that favor one rain type more than the other.
Convective rain is expected to be more frequent with larger rain amounts in the future, especially because it is more sensitive than stratiform rain to the increase in temperature [78]. For example, convective rain has shown a positive trend in all seasons in the Czech Republic [79] and is expected to increase under climate change scenarios [80]. For Switzerland, there is an increase in the annual occurrence of convective weather types [81] and summer convective rain at high elevations [82]. The proportion of convective rain at elevated altitudes is expected to be higher in the future [83]. The reported trends in the proportion of convective rain, along with our results regarding the strong variation in the proportion of convective rain with GWL, highlight the importance of inspecting rain properties for both rain types separately. In other words, a comparison between general weather types without separating convective and stratiform rain may overestimate or underestimate the differences in the addressed rain properties. This error would be influenced by the different proportions of convective rain among these weather types.

4.3. Rain Microstructure

Differences in the rain microstructure were detected between GWL classes for both rain types. These differences were demonstrated by comparing the mean rain DSD and the parameters R, Dm, and N. While the reasons behind these variations for individual GWLs remain largely unclear, the flow directions provide a partial explanation via the associated temperatures and the availability of condensation nuclei and water content.
Particularly in stratiform rain, western and southern circulations bring high water content from the Atlantic and the Mediterranean, which produces high rain intensity. The moisture flux in this area, and generally in the northern hemisphere above 30° N, is westerly and south westerly [84]. Aerosols influence cloud properties by acting as cloud condensation nuclei (CCN) [85]. The aerosol availability appears to be limited for the western, southern, and northwestern circulations in comparison to the northeastern circulations [86]. This is due to anthropogenic activities; a higher concentration of aerosols is reported when the sources are in Russia, Central Europe, and Eastern Europe [87]. Heavily industrialized areas in Germany, the Czech Republic, and Poland are also sources of high particle number concentrations [88]. Consequently, for the study area, the high water content and low CCN in western and southern circulation forces water particles to condensate on a smaller number of nuclei and makes rain drops comparatively large. Conversely, the northern flow direction is associated with low temperatures and forces air parcels to travel a longer distance over terrestrial areas; this lowers the average water content in comparison to other flow directions. Therefore, lower average values of R and Dm were observed. Only in the case of CE, where no flow direction is dominant, did R, Dm, and N exhibit high values, which might indicate a high availability of both CCN and water content. May et al. [89] reported a large number of small drops for high aerosol regimes, but an inverse relation between rain concentration and aerosol concentration in convective clouds. According to Cecchini et al. [90], an increase in CCN leads to higher rain drop concentrations in stratiform rain, and larger rain droplets in convective rain. This falls in line with our conclusions regarding NE–E GWLs, which have higher than average rain concentration in stratiform rain and larger than average rain drop size in convective rain.
Unfortunately, this does not explain the variations between individual GWLs that share the same flow direction. Grouping GWLs by flow direction is not a very precise procedure; the wind direction at higher levels might fluctuate to some extent even within individual GWLs when inspecting a specific location. This means that the source regions and back trajectories might be different within the same GWL [91]. In addition, as the GWL classes change, the site may be influenced by the previous or the upcoming GWL because the classification is done over a large scale. Furthermore, seasonal influences might play a role and there might be an effect of the main alpine ridge, especially for the south and east flow directions, as well as of the mountainous borders between Switzerland and France for the north and west flow directions [92,93,94].
Variations in the rain microstructure between GWLs and flow directions were also detected for convective rain. However, the patterns of these differences were different than the ones for stratiform rain. It might be that, during convective rain, the water content is already sufficiently high. R, N and Dm might be influenced largely by rain formation microscale processes, the height of freezing levels or the boundary layer relative humidity [24], and the local aspects such as topography [92]. All of these might act in combination with the influence of the general weather conditions and produce the observed variation. In other words, GWLs seem to provide conditions that stimulate specific regional and local processes, which enhance or suppress specific rain-forming processes, which in turn influence the observed rain DSD for both rain types.
In a study carried out in Leon, Spain, Fernandez-Raga et al. [53] found that rain drops associated with the northern flow direction had a smaller size compared to other flow directions. This is because most of the moisture transported from the north would precipitate before reaching the measurement site. Conversely, the high Atlantic moisture causes large rain drop size to be associated with western flows. Our results also reveal that GWLs associated with northern flow directions (NE–E and NW–N) had smaller rain drops compared to other flow directions, with the exception of NE–E for convective rain. Our results are in agreement despite using different classifications of the large-scale weather circulations and different locations within Europe. On the other hand, it appears in the reported results of Hachani et al. [29] that northeast circulations are characterized by low concentrations and large drops for the Cévennes–Vivarais region in France. The results also discuss the weak influence of the distance from the Mediterranean Sea, the seasonal influence, the rain type influence, and a combination of these effects. However, the combined effect of rain type and synoptic weather patterns was not addressed, which might be the main reason for the different observation regarding northeast flow direction.

4.4. The Z–R Relation

Jaffrain and Berne [71] demonstrated the spatial variation of the A and b values for a selection of 36 events in the same dataset. In this study, we obtained similar values using the entire dataset. In addition, we demonstrated that the GWL-specific variation exceeds the 1-km2 spatial variation of the A and b values for both rain types. This led to an improved estimation of the rain amount when accounting for the GWL variation over the entire measurement duration. This improvement was particularly high for some individual GWLs, especially those with distinct values of Dm and N, such as SEZ and WW in stratiform rain and WW and HM in convective rain. Interestingly, these GWLs were frequently encountered (Table 1), which rules out the concern of small sample size effect. The rain amount overestimation within 1 km2, which can reach up to +15% as reported by Jaffrain and Berne [71], appears to be propagated to the rain amount estimation within individual GWLs.
The different synoptic features of GWLs at different locations (e.g., one station gets southerly maritime wind for one GWL whereas another gets eastward continental winds for the same GWL) may result in differing rain microstructures at these locations. Due to this local effect of GWLs, GWL models have to be calibrated for each station specifically.
Unfortunately, the number of intervals for each device within each GWL is not large enough to draw decisive conclusions about the spatial variation of the rain estimation within each GWL. A longer measurement period covering a larger number of rain events within each GWL may lead to more concrete conclusions, especially if associated with more precise wind directions at high elevations. Ground measurements over a wider area might help our understanding of the complexity of the interaction between the flow directions at different elevations and the topography and their influence on the rain microstructure.

5. Conclusions

Ground measurements of the rain drop size distribution (DSD) recorded by 16 disdrometers in the period of December 2008–September 2010 during the EPFL-LTE campaign were separated into convective and stratiform intervals and then combined with records of general weather patterns (GWL) to investigate the variations in the rain microstructure between the GWLs.
Convective rain proportions varied among GWLs in both duration and rain amount. These variations along with the previously established influence of rain type on rain DSD suggest that it is important to take the rain type into account when comparing GWLs.
The highest rain amounts and longest rain durations were recorded for the GWLs TRW, SWZ, and WZ. Consequently, these GWLs controlled the total averaged rain parameters. Nevertheless, other GWLs had different rain DSDs. The variation was stronger near the peak of the rain DSD. Significant differences were detected in the values of the rain intensity R, the mass weighted mean diameter Dm, and the rain concentration N. GWLs associated with high averaged R also recorded large rain drops and vice versa.
The values of R, Dm, and N were significantly different between flow directions. In the case of stratiform rain, northern flow (NE–E and NW–N) recorded the smallest average drop size and lowest average R values. S, W, and CE circulations had large drops and high R values. High numbers of drops were recorded in GWLs associated with CE and NE–E. Variations also exist in the case of convective rain; however, the pattern is different and might be affected by local conditions.
The parameters of the Z–R relation varied significantly between GWLs, and estimating R based on the GWL-specific Z–R relations improved the total rain amount estimation for the entire dataset and for both rain types. The improvement is highest for individual GWLs, which revealed distinct rain microstructures such as SEZ and WW in stratiform rain and WW and HM in convective rain.
To our knowledge, this is the first study in Central Europe linking rain DSD to synoptic weather types and general flow directions for each individual rain type. The effect of the described variations with GWL and the flow direction, e.g., on the Z–R parameters, might improve the current radar estimation of R. In future studies, the microstructure of extreme and heavy rain within each GWL, the role of the wind direction at high levels, and improved separation methods of convective and stratiform rain should be addressed to reveal more about the properties of rain within large-scale circulations. However, addressing the inherent spatial and temporal variability of the rain microstructure within each GWL calls for a larger dataset to provide sufficient rain measurements within each GWL and to support these results.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/10/6/811/s1, Table S1: “Accumulated rain duration and rain amount per disdrometer”, Figure S1: “Normalized rain DSD for a selection of GWLs in stratiform rain”, Figure S2: “Normalized rain DSD for a selection of GWLs in Convective rain”.

Author Contributions

Wael Ghada and Annette Menzel conceptualized the research idea. Wael Ghada performed the data processing with support from Allan Buras and Marvin Lüpke. Wael Ghada wrote the manuscript. All authors contributed to the interpretation of results and the editing of the manuscript.

Acknowledgments

We thank those behind the EPFL-LTE campaign 2008–2010 for the published raw DSD records, the Deutscher Wetterdienst (German Meteorological Service-DWD) for providing records of GWLs, and Clemens Wastl for his insight regarding the influence of GWLs. This work was supported by the German Research Foundation (DFG) and the Technical University of Munich (TUM) in the framework of the Open Access Publishing Program. The first author thanks the Deutscher Akademischer Austauschdienst (DAAD) for financial support. We appreciate the valuable comments provided by four anonymous reviewers.

Conflicts of Interest

The authors declare no conflict of interest. The founding sponsors had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript; and in the decision to publish the results.

Appendix A

The following equations were used to calculate the key rain properties for each time step based on the disdrometer raw output.
  • Rain intensity (R) (mm·h−1) [16]
    R = 60 × 60 × π / ( 6 × 1000000   ∆ T ) ∑ i = 1 i = 32 ∑ j = 1 j = 32 ( x i , j   D i 3 / A i )
    x i , j : Detected number of drops that fall in diameter range i and velocity range j.
    ∆ T (s): Temporal resolution = 60 s in this case.
    A i   (m2): Corrected detection area [60]: A i = 180 × ( 30 − D i / 2 ) / 1000000 .
    D i   (mm): Mean diameter of drops that fall in diameter range i.
  • Reflectivity (Z) (mm6·m−3) [16]
    Z = ∑ i = 1 i = 32 ∑ j = 1 j = 32 ( x i , j   D i 6 / ( A i   V j ∆ T ) )
    V j ( m · s − 1 ) : Mean velocity of drops in velocity range j.
    The reflectivity is usually expressed in another unit [dBZ]:
    Z [ d B Z ] = 10 × log 10 ( Z [ mm 6 ·   m − 3 ] ) .
  • Total drop concentration (N) (m−3), i.e., the total number of drops per m3 [16]:
    N = ∑ i = 1 i = 32 ∑ j = 1 j = 32 x i , j / ( V j   ∆ T   W i   A i )
    W i (mm): Width of a diameter range i.
  • Mass weighted diameter (Dm) (mm) [61]:
    D m = ∑ i = 1 i = 32 ∑ j = 1 j = 32 ( x i , j   D i 4 ) ∑ i = 1 i = 32 ∑ j = 1 j = 32 ( x i , j   D i 3 ) .

References

  1. Hazenberg, P.; Yu, N.; Boudevillain, B.; Delrieu, G.; Uijlenhoet, R. Scaling of raindrop size distributions and classification of radar reflectivity–rain rate relations in intense Mediterranean precipitation. J. Hydrol. 2011, 402, 179–192. [Google Scholar] [CrossRef]
  2. Lal, R. Soil Erosion Research Methods, 2nd ed.; Soil and Water Conservation Society; St. Lucie Press: Ankeny, IA, USA, 1994. [Google Scholar]
  3. Angulo-Martínez, M.; Barros, A.P. Measurement uncertainty in rainfall kinetic energy and intensity relationships for soil erosion studies: An evaluation using PARSIVEL disdrometers in the Southern Appalachian Mountains. Geomorphology 2015, 228, 28–40. [Google Scholar] [CrossRef]
  4. Murphy, L.U.; Cochrane, T.A.; O’Sullivan, A. Build-up and wash-off dynamics of atmospherically derived Cu, Pb, Zn and TSS in stormwater runoff as a function of meteorological characteristics. Sci. Total Environ. 2015, 508, 206–213. [Google Scholar] [CrossRef] [PubMed]
  5. Moupfouma, F.; Martin, L. Modelling of the rainfall rate cumulative distribution for the design of satellite and terrestrial communication systems. Int. J. Satell. Commun. Netw. 1995, 13, 105–115. [Google Scholar] [CrossRef]
  6. Shkarofsky, I. Dependence of rain attenuation and cross-polarization on drop size distribution. IEEE Trans. Antennas Propag. 1979, 27, 538–542. [Google Scholar] [CrossRef]
  7. Thurai, M.; Gatlin, P.N.; Bringi, V.N. Separating stratiform and convective rain types based on the drop size distribution characteristics using 2D video disdrometer data. Atmos. Res. 2016, 169, 416–423. [Google Scholar] [CrossRef]
  8. Caracciolo, C.; Porcù, F.; Prodi, F. Precipitation classification at mid-latitudes in terms of drop size distribution parameters. Adv. Geosci. 2008, 16, 11–17. [Google Scholar] [CrossRef]
  9. Tapiador, F.J.; Navarro, A.; Moreno, R.; Jiménez-Alcázar, A.; Marcos, C.; Tokay, A.; Durán, L.; Bodoque, J.M.; Martín, R.; Petersen, W. On the Optimal Measuring Area for Pointwise Rainfall Estimation: A Dedicated Experiment with 14 Laser Disdrometers. J. Hydrometeorol. 2017, 18, 753–760. [Google Scholar] [CrossRef]
  10. Jaffrain, J.; Studzinski, A.; Berne, A. A network of disdrometers to quantify the small-scale variability of the raindrop size distribution. Water Resour. Res. 2011, 47, W00H06. [Google Scholar] [CrossRef]
  11. Jaffrain, J.; Berne, A. Quantification of the Small-Scale Spatial Structure of the Raindrop Size Distribution from a Network of Disdrometers. J. Appl. Meteorol. Climatol. 2012, 51, 941–953. [Google Scholar] [CrossRef]
  12. Jameson, A.R.; Larsen, M.L.; Kostinski, A.B. Disdrometer Network Observations of Finescale Spatial–Temporal Clustering in Rain. J. Atmos. Sci. 2015, 72, 1648–1666. [Google Scholar] [CrossRef]
  13. Das, S.; Maitra, A. Characterization of tropical precipitation using drop size distribution and rain rate-radar reflectivity relation. Theor. Appl. Climatol. 2018, 132, 275–286. [Google Scholar] [CrossRef]
  14. Gatlin, P.N.; Thurai, M.; Bringi, V.N.; Petersen, W.; Wolff, D.; Tokay, A.; Carey, L.; Wingo, M. Searching for Large Raindrops: A Global Summary of Two-Dimensional Video Disdrometer Observations. J. Appl. Meteorol. Climatol. 2015, 54, 1069–1089. [Google Scholar] [CrossRef]
  15. Bringi, V.N.; Chandrasekar, V.; Hubbert, J.; Gorgucci, E.; Randeu, W.L.; Schoenhuber, M. Raindrop Size Distribution in Different Climatic Regimes from Disdrometer and Dual-Polarized Radar Analysis. J. Atmos. Sci. 2003, 60, 354–365. [Google Scholar] [CrossRef]
  16. Chen, B.; Wang, J.; Gong, D. Raindrop Size Distribution in a Midlatitude Continental Squall Line Measured by Thies Optical Disdrometers over East China. J. Appl. Meteorol. Climatol. 2016, 55, 621–634. [Google Scholar] [CrossRef]
  17. Maki, M.; Keenan, T.D.; Sasaki, Y.; Nakamura, K. Characteristics of the Raindrop Size Distribution in Tropical Continental Squall Lines Observed in Darwin, Australia. J. Appl. Meteorol. 2001, 40, 1393–1412. [Google Scholar] [CrossRef]
  18. Islam, T.; Rico-Ramirez, M.A.; Thurai, M.; Han, D. Characteristics of raindrop spectra as normalized gamma distribution from a Joss–Waldvogel disdrometer. Atmos. Res. 2012, 108, 57–73. [Google Scholar] [CrossRef]
  19. Hu, Z.; Srivastava, R.C. Evolution of Raindrop Size Distribution by Coalescence, Breakup, and Evaporation: Theory and Observations. J. Atmos. Sci. 1995, 52, 1761–1783. [Google Scholar] [CrossRef]
  20. Villermaux, E.; Bossa, B. Single-drop fragmentation determines size distribution of raindrops. Nat. Phys. 2009, 5, 697–702. [Google Scholar] [CrossRef]
  21. Kumjian, M.R.; Ryzhkov, A.V. The Impact of Evaporation on Polarimetric Characteristics of Rain: Theoretical Model and Practical Implications. J. Appl. Meteorol. Climatol. 2010, 49, 1247–1267. [Google Scholar] [CrossRef]
  22. Rosenfeld, D.; Mintz, Y. Evaporation of Rain Falling from Convective Clouds as Derived from Radar Measurements. J. Appl. Meteorol. 1988, 27, 209–215. [Google Scholar] [CrossRef]
  23. Kumjian, M.R.; Ryzhkov, A.V. The Impact of Size Sorting on the Polarimetric Radar Variables. J. Atmos. Sci. 2012, 69, 2042–2060. [Google Scholar] [CrossRef]
  24. Munchak, S.J.; Kummerow, C.D.; Elsaesser, G. Relationships between the Raindrop Size Distribution and Properties of the Environment and Clouds Inferred from TRMM. J. Clim. 2012, 25, 2963–2978. [Google Scholar] [CrossRef]
  25. Berg, W.; L’Ecuyer, T.; van den Heever, S. Evidence for the impact of aerosols on the onset and microphysical properties of rainfall from a combination of satellite observations and cloud-resolving model simulations. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
  26. Givati, A.; Rosenfeld, D. Separation between Cloud-Seeding and Air-Pollution Effects. J. Appl. Meteorol. 2005, 44, 1298–1314. [Google Scholar] [CrossRef]
  27. Harikumar, R. Orographic effect on tropical rain physics in the Asian monsoon region. Atmos. Sci. Lett. 2016, 17, 556–563. [Google Scholar] [CrossRef]
  28. Zwiebel, J.; van Baelen, J.; Anquetin, S.; Pointin, Y.; Boudevillain, B. Impacts of orography and rain intensity on rainfall structure. The case of the HyMeX IOP7a event. Q. J. R. Meteorol. Soc. 2016, 142, 310–319. [Google Scholar] [CrossRef]
  29. Hachani, S.; Boudevillain, B.; Delrieu, G.; Bargaoui, Z. Drop Size Distribution Climatology in Cévennes-Vivarais Region, France. Atmosphere 2017, 8. [Google Scholar] [CrossRef]
  30. Wen, J.; Zhao, K.; Huang, H.; Zhou, B.; Yang, Z.; Chen, G.; Wang, M.; Wen, L.; Dai, H.; Xu, L.; et al. Evolution of microphysical structure of a subtropical squall line observed by a polarimetric radar and a disdrometer during OPACC in Eastern China. J. Geophys. Res. 2017, 122, 8033–8050. [Google Scholar] [CrossRef]
  31. Steiner, M.; Smith, J.A. Convective versus stratiform rainfall: An ice-microphysical and kinematic conceptual model. Atmos. Res. 1998, 47-48, 317–326. [Google Scholar] [CrossRef]
  32. Rosenfeld, D.; Ulbrich, C.W. Cloud Microphysical Properties, Processes, and Rainfall Estimation Opportunities. In Radar and Atmospheric Science: A Collection of Essays in Honor of David Atlas; American Meteorological Society: Boston, MA, USA, 2003. [Google Scholar]
  33. Campos, E.F.; Zawadzki, I.; Petitdidier, M.; Fernández, W. Measurement of raindrop size distributions in tropical rain at Costa Rica. J. Hydrol. 2006, 328, 98–109. [Google Scholar] [CrossRef]
  34. Penide, G.; Kumar, V.V.; Protat, A.; May, P.T. Statistics of Drop Size Distribution Parameters and Rain Rates for Stratiform and Convective Precipitation during the North Australian Wet Season. Mon. Weather Rev. 2013, 141, 3222–3237. [Google Scholar] [CrossRef]
  35. Huth, R.; Beck, C.; Philipp, A.; Demuzere, M.; Ustrnul, Z.; Cahynová, M.; Kyselý, J.; Tveito, O.E. Classifications of atmospheric circulation patterns: Recent advances and applications. Ann. N. Y. Acad. Sci. 2008, 1146, 105–152. [Google Scholar] [CrossRef] [PubMed]
  36. Ramos, A.M.; Barriopedro, D.; Dutra, E. Circulation weather types as a tool in atmospheric, climate, and environmental research. Front. Environ. Sci. 2015, 3. [Google Scholar] [CrossRef]
  37. Brdossy, A.; Caspary, H.J. Detection of climate change in Europe by analyzing European atmospheric circulation patterns from 1881 to 1989. Theor. Appl. Climatol. 1990, 42, 155–167. [Google Scholar] [CrossRef]
  38. Baur, F.; Hess, P.; Nagel, H. Kalender der Grosswetterlagen Europas 1881–1939. Bad Homburg 1944, 35. [Google Scholar]
  39. Gerstengarbe, F.-W.; Werner, P.C.; Busold, W.; Hess, P.; Brezowsky, H. Katalog der Grosswetterlagen Europas nach Paul Hess und Helmuth Brezowski 1881–1992; 4., vollständig neu bearbeitete Aufl.; Selbstverlag des Deutschen Wetterdienstes: Offenbach am Main, Germany, 1993; p. 244. Available online: https://www.dwd.de/DE/leistungen/pbfb_verlag_berichte/pdf_einzelbaende/113_pdf.pdf?__blob=publicationFile&v=3 (accessed on 23 May 2018).
  40. BUISHAND, T.A.; BRANDSMA, T. Comparison of circulation classification schemes for predicting temperature and precipitation in the Netherlands. Int. J. Climatol. 1997, 17, 875–889. [Google Scholar] [CrossRef]
  41. Cony, M.; Martín, L.; Hernándes, E.; Del Teso, T. Synoptic Patterns That Contribute to Extremely Hot Days in Europe. Available online: http://www.scielo.org.mx/scielo.php?script=sci_arttext&pid=S0187-62362010000400001 (accessed on 9 April 2018).
  42. Steirou, E.; Gerlitz, L.; Apel, H.; Merz, B. Links between large-scale circulation patterns and streamflow in Central Europe: A review. J. Hydrol. 2017, 549, 484–500. [Google Scholar] [CrossRef]
  43. Jacobeit, J.; Glaser, R.; Luterbacher, J.; Wanner, H. Links between flood events in central Europe since AD 1500 and large-scale atmospheric circulation modes. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
  44. Petrow, T.; Merz, B.; Lindenschmidt, K.-E.; Thieken, A.H. Aspects of seasonality and flood generating circulation patterns in a mountainous catchment in south-eastern Germany. Hydrol. Earth Syst. Sci. 2007, 11, 1455–1468. [Google Scholar] [CrossRef]
  45. Wastl, C.; Schunk, C.; Lüpke, M.; Cocca, G.; Conedera, M.; Valese, E.; Menzel, A. Large-scale weather types, forest fire danger, and wildfire occurrence in the Alps. Agric. For. Meteorol. 2013, 168, 15–25. [Google Scholar] [CrossRef]
  46. Nikolopoulos, E.I.; Borga, M.; Marra, F.; Crema, S.; Marchi, L. Debris flows in the eastern Italian Alps: Seasonality and atmospheric circulation patterns. Nat. Hazards Earth Syst. Sci. 2015, 15, 647–656. [Google Scholar] [CrossRef]
  47. Ustrnul, Z.; Czekierda, D. Circulation background of the atmospheric precipitation in Central Europe (based on the Polish example). Meteorol. Z. 2001, 10, 103–111. [Google Scholar] [CrossRef]
  48. Ducić, V.; Luković, J.; Burić, D.; Stanojević, G.; Mustafić, S. Precipitation extremes in the wettest Mediterranean region (Krivošije) and associated atmospheric circulation types. Nat. Hazards Earth Syst. Sci. 2012, 12, 687–697. [Google Scholar] [CrossRef]
  49. Nowosad, J.; Stach, A. Relation between extensive extreme precipitation in Poland and atmospheric circulation. Quaest. Geogr. 2014, 33, 115–129. [Google Scholar] [CrossRef]
  50. Planchon, O.; Quénol, H.; Dupont, N.; Corgne, S. Application of the Hess-Brezowsky classification to the identification of weather patterns causing heavy winter rainfall in Brittany (France). Nat. Hazards Earth Syst. Sci. 2009, 9, 1161–1173. [Google Scholar] [CrossRef]
  51. Hoy, A.; Schucknecht, A.; Sepp, M.; Matschullat, J. Large-scale synoptic types and their impact on European precipitation. Theor. Appl. Climatol. 2014, 116, 19–35. [Google Scholar] [CrossRef]
  52. Blenkinsop, S.; Chan, S.C.; Kendon, E.J.; Roberts, N.M.; Fowler, H.J. Temperature influences on intense UK hourly precipitation and dependency on large-scale circulation. Environ. Res. Lett. 2015, 10. [Google Scholar] [CrossRef]
  53. Fernandez-Raga, M.; Castro, A.; Marcos, E.; Palencia, C.; Fraile, R. Weather types and rainfall microstructure in Leon, Spain. Int. J. Climatol. 2017, 37, 1834–1842. [Google Scholar] [CrossRef]
  54. Berne, A.; Jaffrain, J. GPM Ground Validation NASA EPFL-LTE Parsivel DSD Data Lausanne, Switzerland; NASA Global Hydrology Resource Center DAAC: Huntsville, AL, USA, 2016.
  55. Knittel, J. Großwetterlage: Januar bis Dezember 2008. Available online: https://www.dwd.de/DE/leistungen/grosswetterlage/2008/gwl_zusammenfassung.pdf?__blob=publicationFile&v=3 (accessed on 3 April 2018).
  56. Knittel, J. Großwetterlage: Januar bis Dezember 2009. Available online: https://www.dwd.de/DE/leistungen/grosswetterlage/2009/gwl_zusammenfassung.pdf?__blob=publicationFile&v=3 (accessed on 3 April 2018).
  57. Knittel, J. Großwetterlage: Januar bis Dezember 2010. Available online: https://www.dwd.de/DE/leistungen/grosswetterlage/2010/gwl_zusammenfassung.pdf?__blob=publicationFile&v=3 (accessed on 3 April 2018).
  58. OTT MESSTECHNIK GmbH & Co. K. Present Weather Sensor Parsivel: Operating Instructions. Available online: https://www.esrl.noaa.gov/psd/data/obs/instruments/OpticalDisdrometer.pdf (accessed on 29 March 2018).
  59. Löffler-Mang, M.; Joss, J. An Optical Disdrometer for Measuring Size and Velocity of Hydrometeors. J. Atmos. Ocean. Technol. 2000, 17, 130–139. [Google Scholar] [CrossRef]
  60. Raupach, T.H.; Berne, A. Correction of raindrop size distributions measured by Parsivel disdrometers, using a two-dimensional video disdrometer as a reference. Atmos. Meas. Tech. 2015, 8, 343–365. [Google Scholar] [CrossRef]
  61. Marzuki, M.; Randeu, W.L.; Schönhuber, M.; Bringi, V.N.; Kozu, T.; Shimomai, T. Raindrop Size Distribution Parameters of Distrometer Data With Different Bin Sizes. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3075–3080. [Google Scholar] [CrossRef]
  62. Marzano, F.S.; Cimini, D.; Montopoli, M. Investigating precipitation microphysics using ground-based microwave remote sensors and disdrometer data. Atmos. Res. 2010, 97, 583–600. [Google Scholar] [CrossRef]
  63. Tokay, A.; Petersen, W.A.; Gatlin, P.; Wingo, M. Comparison of Raindrop Size Distribution Measurements by Collocated Disdrometers. J. Atmos. Ocean. Technol. 2013, 30, 1672–1690. [Google Scholar] [CrossRef]
  64. Friedrich, K.; Kalina, E.A.; Masters, F.J.; Lopez, C.R. Drop-Size Distributions in Thunderstorms Measured by Optical Disdrometers during VORTEX2. Mon. Weather Rev. 2013, 141, 1182–1203. [Google Scholar] [CrossRef]
  65. Atlas, D.; Srivastava, R.C.; Sekhon, R.S. Doppler radar characteristics of precipitation at vertical incidence. Rev. Geophys. 1973, 11, 1–35. [Google Scholar] [CrossRef]
  66. Willmott, C.J.; Matsuura, K. Advantages of the mean absolute error (MAE) over the root mean square error (RMSE) in assessing average model performance. Clim. Res. 2005, 30, 79–82. [Google Scholar] [CrossRef]
  67. Team, R.C. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2017; Available online: https://www.R-project.org/ (accessed on 22 May 2018).
  68. Team, R. RStudio. Integrated Development Environment for R; RStudio Inc.: Boston, MA, USA, 2016; Available online: http://www.rstudio.com/ (accessed on 22 May 2018).
  69. Wickham, H. ggplot2. Elegant Graphics for Data Analysis; Springer: New York, NY, USA, 2009. [Google Scholar]
  70. Testud, J.; Oury, S.; Black, R.A.; Amayenc, P.; Dou, X. The Concept of “Normalized” Distribution to Describe Raindrop Spectra: A Tool for Cloud Physics and Cloud Remote Sensing. J. Appl. Meteorol. 2001, 40, 1118–1140. [Google Scholar] [CrossRef]
  71. Jaffrain, J.; Berne, A. Influence of the Subgrid Variability of the Raindrop Size Distribution on Radar Rainfall Estimators. J. Appl. Meteorol. Climatol. 2012, 51, 780–785. [Google Scholar] [CrossRef]
  72. Cahynová, M.; Huth, R. Enhanced lifetime of atmospheric circulation types over Europe: Fact or fiction? Tellus A 2009, 61, 407–416. [Google Scholar] [CrossRef]
  73. Tokay, A.; Short, D.A. Evidence from Tropical Raindrop Spectra of the Origin of Rain from Stratiform versus Convective Clouds. J. Appl. Meteorol. 1996, 35, 355–371. [Google Scholar] [CrossRef]
  74. Bukovčić, P.; Zrnić, D.; Zhang, G. Convective–stratiform separation using video disdrometer observations in central Oklahoma—The Bayesian approach. Atmos. Res. 2015, 155, 176–191. [Google Scholar] [CrossRef]
  75. Williams, C.R.; Ecklund, W.L.; Gage, K.S. Classification of Precipitating Clouds in the Tropics Using 915-MHz Wind Profilers. J. Atmos. Ocean. Technol. 1995, 12, 996–1012. [Google Scholar] [CrossRef]
  76. Rulfová, Z.; Kyselý, J. Trends of Convective and Stratiform Precipitation in the Czech Republic, 1982–2010. Adv. Meteorol. 2014, 2014, 1–11. [Google Scholar] [CrossRef]
  77. Yang, S.; Smith, E.A. Convective–Stratiform Precipitation Variability at Seasonal Scale from 8 Yr of TRMM Observations: Implications for Multiple Modes of Diurnal Variability. J. Clim. 2008, 21, 4087–4114. [Google Scholar] [CrossRef]
  78. Berg, P.; Moseley, C.; Haerter, J.O. Strong increase in convective precipitation in response to higher temperatures. Nat. Geosci 2013, 6, 181–185. [Google Scholar] [CrossRef]
  79. Rulfová, Z.; Kyselý, J. Disaggregating convective and stratiform precipitation from station weather data. Atmos. Res. 2013, 134, 100–115. [Google Scholar] [CrossRef]
  80. Rulfová, Z.; Beranová, R.; Kyselý, J. Climate change scenarios of convective and large-scale precipitation in the Czech Republic based on EURO-CORDEX data. Int. J. Climatol. 2017, 37, 2451–2465. [Google Scholar] [CrossRef]
  81. Stefanicki, G.; Talkner, P.; Weber, R.O. Frequency Changes of Weather Types in the Alpine Region since 1945. Theor. Appl. Climatol. 1998, 60, 47–61. [Google Scholar] [CrossRef]
  82. Giorgi, F.; Torma, C.; Coppola, E.; Ban, N.; Schär, C.; Somot, S. Enhanced summer convective rainfall at Alpine high elevations in response to climate warming. Nat. Geosci 2016, 9, 584–589. [Google Scholar] [CrossRef]
  83. Fischer, A.M.; Keller, D.E.; Liniger, M.A.; Rajczak, J.; Schär, C.; Appenzeller, C. Projected changes in precipitation intensity and frequency in Switzerland: A multi-model perspective. Int. J. Climatol. 2015, 35, 3204–3219. [Google Scholar] [CrossRef]
  84. Van der Ent, R.J.; Savenije, H.H.G.; Schaefli, B.; Steele-Dunne, S.C. Origin and fate of atmospheric moisture over continents. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef]
  85. Lohmann, U.; Feichter, J. Global indirect aerosol effects: A review. Atmos. Chem. Phys. 2005, 5, 715–737. [Google Scholar] [CrossRef]
  86. Ackermann, I.J.; Hass, H.; Memmesheimer, M.; Ebel, A.; Binkowski, F.S.; Shankar, U. Modal aerosol dynamics model for Europe. Atmos. Environ. 1998, 32, 2981–2999. [Google Scholar] [CrossRef]
  87. Birmili, W.; Wiedensohler, A.; Heintzenberg, J.; Lehmann, K. Atmospheric particle number size distribution in central Europe: Statistical relations to air masses and meteorology. J. Geophys. Res. 2001, 106, 32005–32018. [Google Scholar] [CrossRef]
  88. Byčenkienė, S.; Plauškaitė, K.; Dudoitis, V.; Ulevicius, V. Urban background levels of particle number concentration and sources in Vilnius, Lithuania. Atmos. Res. 2014, 143, 279–292. [Google Scholar] [CrossRef]
  89. May, P.T.; Bringi, V.N.; Thurai, M. Do We Observe Aerosol Impacts on DSDs in Strongly Forced Tropical Thunderstorms? J. Atmos. Sci. 2011, 68, 1902–1910. [Google Scholar] [CrossRef]
  90. Cecchini, M.A.; Machado, L.A.T.; Artaxo, P. Droplet Size Distributions as a function of rainy system type and Cloud Condensation Nuclei concentrations. Atmos. Res. 2014, 143, 301–312. [Google Scholar] [CrossRef]
  91. Hondula, D.M.; Sitka, L.; Davis, R.E.; Knight, D.B.; Gawtry, S.D.; Deaton, M.L.; Lee, T.R.; Normile, C.P.; Stenger, P.J. A back-trajectory and air mass climatology for the Northern Shenandoah Valley, USA. Int. J. Climatol. 2010, 30, 569–581. [Google Scholar] [CrossRef]
  92. Fuhrer, O.; Schär, C. Embedded Cellular Convection in Moist Flow past Topography. J. Atmos. Sci. 2005, 62, 2810–2828. [Google Scholar] [CrossRef]
  93. Cotton, W.R.; Bryan, G.; van den Heever, S.C. The Influence of Mountains on Airflow, Clouds, and Precipitation. In Storm and Cloud Dynamics: The Dynamics of Clouds and Precipitating Mesoscale Systems, 2nd ed.; Cotton, W.R., Bryan, G.H., van den Heever, S.C., Eds.; Academic Press: Burlington, MA, USA, 2011; pp. 673–750. [Google Scholar]
  94. Rotunno, R.; Houze, R.A. Lessons on orographic precipitation from the Mesoscale Alpine Programme. Q. J. R. Meteorol. Soc. 2007, 133, 811–830. [Google Scholar] [CrossRef]
Remotesensing 10 00811 g001 550
Figure 1. (a) A bar plot of accumulated rain duration in hours; (b) a bar plot of accumulated rain amount in mm; and (c) a boxplot of rain intensities in mm·h−1 for each rain type at Lausanne, Switzerland (December 2008–September 2010). Error bars in panels (a) and (b) are based on the standard error across devices. In panel (c) outliers are not shown, medians (means) are represented by the horizontal thick lines (black points), and the lower and upper hinges represent the first and third quartiles, while the upper (lower) whisker extends from the upper (lower) hinge to the largest (smallest) value no further than 1.5 times the interquartile range from the hinge [69].
Figure 1. (a) A bar plot of accumulated rain duration in hours; (b) a bar plot of accumulated rain amount in mm; and (c) a boxplot of rain intensities in mm·h−1 for each rain type at Lausanne, Switzerland (December 2008–September 2010). Error bars in panels (a) and (b) are based on the standard error across devices. In panel (c) outliers are not shown, medians (means) are represented by the horizontal thick lines (black points), and the lower and upper hinges represent the first and third quartiles, while the upper (lower) whisker extends from the upper (lower) hinge to the largest (smallest) value no further than 1.5 times the interquartile range from the hinge [69].
Remotesensing 10 00811 g001
Remotesensing 10 00811 g002 550
Figure 2. (a) Bar plots of the accumulated rain duration in hours; (b) proportion of the convective rain duration averaged over the 16 devices for each GWL (see Table 1); and (c) proportion of the convective rain amount averaged over the 16 devices for each GWL. Error bars are based on the standard error across devices. GWLs are grouped by flow direction and within each flow direction ordered by accumulated rain duration over all disdrometers. Dashed lines represent the overall proportion of the convective rain duration in panel (b) and the convective rain amount in panel (c).
Figure 2. (a) Bar plots of the accumulated rain duration in hours; (b) proportion of the convective rain duration averaged over the 16 devices for each GWL (see Table 1); and (c) proportion of the convective rain amount averaged over the 16 devices for each GWL. Error bars are based on the standard error across devices. GWLs are grouped by flow direction and within each flow direction ordered by accumulated rain duration over all disdrometers. Dashed lines represent the overall proportion of the convective rain duration in panel (b) and the convective rain amount in panel (c).
Remotesensing 10 00811 g002
Remotesensing 10 00811 g003 550
Figure 3. Proportion of convective rain (a) duration and (b) amount averaged over the 16 devices within each flow direction (cf. Table 1). Error bars are based on the standard error. Dashed lines represent the overall proportion of the convective rain duration and amount.
Figure 3. Proportion of convective rain (a) duration and (b) amount averaged over the 16 devices within each flow direction (cf. Table 1). Error bars are based on the standard error. Dashed lines represent the overall proportion of the convective rain duration and amount.
Remotesensing 10 00811 g003
Remotesensing 10 00811 g004 550
Figure 4. Mean concentrations (number of drops per 1 m3 of air volume and per 1 mm of the diameter range (A4)) in (a) stratiform rain and (b) convective rain. To aid the interpretation, the plot is limited to a selection of GWLs that demonstrated distinct DSDs. The dashed black line indicates the mean DSD in both rain types regardless of GWL.
Figure 4. Mean concentrations (number of drops per 1 m3 of air volume and per 1 mm of the diameter range (A4)) in (a) stratiform rain and (b) convective rain. To aid the interpretation, the plot is limited to a selection of GWLs that demonstrated distinct DSDs. The dashed black line indicates the mean DSD in both rain types regardless of GWL.
Remotesensing 10 00811 g004
Remotesensing 10 00811 g005 550
Figure 5. Scatter plot of the rain parameters per GWL with the mean mass weighted diameter (Dm) on the horizontal axis and the mean concentration (N) on the vertical axis. The size of each dot corresponds to the rain intensity (R) associated with a particular GWL. The colors indicate the five considered flow directions (cf. Table 1) in (a) stratiform rain and (b) convective rain. The horizontal lines represent the standard error of Dm. The vertical lines represent the standard error of N.
Figure 5. Scatter plot of the rain parameters per GWL with the mean mass weighted diameter (Dm) on the horizontal axis and the mean concentration (N) on the vertical axis. The size of each dot corresponds to the rain intensity (R) associated with a particular GWL. The colors indicate the five considered flow directions (cf. Table 1) in (a) stratiform rain and (b) convective rain. The horizontal lines represent the standard error of Dm. The vertical lines represent the standard error of N.
Remotesensing 10 00811 g005
Remotesensing 10 00811 g006 550
Figure 6. Scatter plot of rain parameters for each flow direction with the mean mass weighted diameter (Dm) for each flow direction on the horizontal axis and the mean concentration (N) for each flow direction on the vertical axis. The size of each dot represents the rain intensity associated with the corresponding flow direction. The colors indicate the five flow directions (see Table 1) in (a) stratiform rain and (b) convective rain. The horizontal lines represent the standard error of Dm. The vertical lines represent the standard error of N. Note the difference in absolute values for the two panels.
Figure 6. Scatter plot of rain parameters for each flow direction with the mean mass weighted diameter (Dm) for each flow direction on the horizontal axis and the mean concentration (N) for each flow direction on the vertical axis. The size of each dot represents the rain intensity associated with the corresponding flow direction. The colors indicate the five flow directions (see Table 1) in (a) stratiform rain and (b) convective rain. The horizontal lines represent the standard error of Dm. The vertical lines represent the standard error of N. Note the difference in absolute values for the two panels.
Remotesensing 10 00811 g006
Remotesensing 10 00811 g007 550
Figure 7. A and b values for the GWL Z–R model (white circles) and the 16 devices (dots) in (a) stratiform and (b) convective rain. The grey area represents the range of A and b values as they vary spatially (across the devices).
Figure 7. A and b values for the GWL Z–R model (white circles) and the 16 devices (dots) in (a) stratiform and (b) convective rain. The grey area represents the range of A and b values as they vary spatially (across the devices).
Remotesensing 10 00811 g007
Remotesensing 10 00811 g008 550
Figure 8. Relative error (RE) of the accumulated rain amount estimated by the global Z–R model (black) and the GWL Z–R model (grey) for (a) stratiform rain and (b) convective rain.
Figure 8. Relative error (RE) of the accumulated rain amount estimated by the global Z–R model (black) and the GWL Z–R model (grey) for (a) stratiform rain and (b) convective rain.
Remotesensing 10 00811 g008
Table
Table 1. General weather patterns (GWLs) according to Hess and Brezowsky [39] and their classification based on the flow direction [50]. This table also includes the accumulated rain duration over all devices for each GWL in both rain types. Gray cells indicate GWLs with small sample sizes, which are not further considered in the analyses.
Table 1. General weather patterns (GWLs) according to Hess and Brezowsky [39] and their classification based on the flow direction [50]. This table also includes the accumulated rain duration over all devices for each GWL in both rain types. Gray cells indicate GWLs with small sample sizes, which are not further considered in the analyses.
Flow DirectionGWLAccumulated Duration [min]
ConvectiveStratiform
W:
Westerly		WAAnticyclonic Westerly2441
WZCyclonic Westerly12,10179,492
WSSouth-Shifted Westerly128835,715
WWMaritime Westerly 345430,797
S:
Southerly		SWAAnticyclonic Southwesterly6234404
SAAnticyclonic Southerly00
SEAAnticyclonic Southeasterly94954
SWZCyclonic Southwesterly15,12983,369
SZCyclonic Southerly5296
TBLow over the British Isles10017703
TRWTrough over Western Europe8979137,716
SEZCyclonic Southeasterly3711,670
NW–N:
Northwesterly, Northerly		NWAAnticyclonic Northwesterly0121
NAAnticyclonic Northerly00
HNAIcelandic High, Ridge C.E. *00
HBHigh over the British Isles1883
NWZCyclonic Northwesterly171420,052
NZCyclonic Northerly15074573
HNZIcelandic High, Trough C.E.107613,672
TRMTrough over C.E.596732,031
CE:
Main high/low pressure area over Central Europe (no specific prevailing direction)		HMHigh over C.E.26736464
TMLow (Cut-Off) over C.E.215713,966
BMRidge across C.E.335818,977
NE–E:
Northeasterly, Easterly		NEAAnticyclonic Northeasterly0977
HFAScandinavian High, Ridge C.E.6967734
HNFAHigh Scandinavia-Iceland, Ridge C.E.00
NEZCyclonic Northeasterly1293711
HFZScandinavian High, Trough C.E.06756
HNFZHigh Scandinavia-Iceland, Trough C.E.9249361
-UTransitional00
* Central Europe (C.E.).
Table
Table 2. Mean average error (MAE) in the rain rate R [mm·h−1] calculated by the GWL Z–R model and the general Z–R relation. The values are given for the entire dataset and for each rain type separately.
Table 2. Mean average error (MAE) in the rain rate R [mm·h−1] calculated by the GWL Z–R model and the general Z–R relation. The values are given for the entire dataset and for each rain type separately.
Whole Dataset Stratiform Rain Convective Rain
Global model0.5840.3572.52
GWL model 0.550.3452.3

Share and Cite

MDPI and ACS Style

Ghada, W.; Buras, A.; Lüpke, M.; Schunk, C.; Menzel, A. Rain Microstructure Parameters Vary with Large-Scale Weather Conditions in Lausanne, Switzerland. Remote Sens. 2018, 10, 811. https://doi.org/10.3390/rs10060811

AMA Style

Ghada W, Buras A, Lüpke M, Schunk C, Menzel A. Rain Microstructure Parameters Vary with Large-Scale Weather Conditions in Lausanne, Switzerland. Remote Sensing. 2018; 10(6):811. https://doi.org/10.3390/rs10060811

Chicago/Turabian Style

Ghada, Wael, Allan Buras, Marvin Lüpke, Christian Schunk, and Annette Menzel. 2018. "Rain Microstructure Parameters Vary with Large-Scale Weather Conditions in Lausanne, Switzerland" Remote Sensing 10, no. 6: 811. https://doi.org/10.3390/rs10060811

APA Style

Ghada, W., Buras, A., Lüpke, M., Schunk, C., & Menzel, A. (2018). Rain Microstructure Parameters Vary with Large-Scale Weather Conditions in Lausanne, Switzerland. Remote Sensing, 10(6), 811. https://doi.org/10.3390/rs10060811

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop