Remote Sensing of Phytoplankton Size Class in Northwest Atlantic from 1998 to 2016: Bio-Optical Algorithms Comparison and Application
Abstract
:1. Introduction
2. Materials and Methods
2.1. In Situ Measurements
2.2. Satellite Data
2.2.1. Satellite Dataset
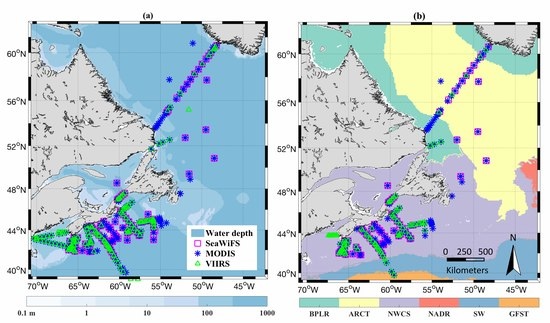
2.2.2. Biogeochemical Provinces and Climate Change Compatible Time Series of Ocean Color in the NWA
2.3. PSC Algorithms and Ranking Method
2.3.1. PSC Algorithms
2.3.2. Algorithm Assessment Method
2.4. Accuracy Assessment
3. Results
3.1. PSC Algorithm Comparison Results
3.1.1. SeaWiFS
3.1.2. MODIS
3.1.3. VIIRS
4. Discussion
4.1. Uncertainties Associated with Satellite-Derived Inputs
4.1.1. OCx Chla Products
4.1.2. Phytoplankton Absorption Coefficient Products
4.2. Model Selection for Monitoring PSC in the NWA
4.3. PSC in Northwest Atlantic
4.3.1. Temporal Variation of Microphytoplankton in NWA
4.3.2. Anomaly Analysis of Microphytoplankton in NWA
4.3.3. Discussion on the Microphytoplankton Variation in NWA
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- International Ocean-Colour Coordinating Group (IOCCG). Phytoplankton Functional Types from Space; International Ocean-Colour Coordinating Group: Dartmouth, NS, Canada, 2014. [Google Scholar]
- Sieburth, J.M.; Smetacek, V.; Lenz, J. Pelagic ecosystem structure: Heterotrophic compartments of the plankton and their relationship to plankton size fractions. Limnol. Oceanogr. 1978, 23, 1256–1263. [Google Scholar] [CrossRef]
- Marañón, E. Cell size as a key determinant of phytoplankton metabolism and community structure. Annu. Rev. Mar. Sci. 2015, 7, 241–264. [Google Scholar] [CrossRef] [PubMed]
- Finkel, Z.V.; Beardall, J.; Flynn, K.J.; Quigg, A.; Rees, T.A.V.; Raven, J.A. Phytoplankton in a changing world: Cell size and elemental stoichiometry. J. Plankton Res. 2009, 32, 119–137. [Google Scholar] [CrossRef]
- Irwin, A.J. Scaling-up from nutrient physiology to the size-structure of phytoplankton communities. J. Plankton Res. 2006, 28, 459–471. [Google Scholar] [CrossRef] [Green Version]
- Nair, A.; Sathyendranath, S.; Platt, T.; Morales, J.; Stuart, V.; Forget, M.-H.; Devred, E.; Bouman, H. Remote sensing of phytoplankton functional types. Remote Sens. Environ. 2008, 112, 3366–3375. [Google Scholar] [CrossRef]
- Key, T.; McCarthy, A.; Campbell, D.A.; Six, C.; Roy, S.; Finkel, Z.V. Cell size trade-offs govern light exploitation strategies in marine phytoplankton. Environ. Microbiol. 2010, 12, 95–104. [Google Scholar] [CrossRef] [PubMed]
- Kirk, J.T.O. Light and Photosynthesis in Aquatic Ecosystems, 3rd ed.; Cambridge University Press: Cambridge, UK, 2011; ISBN 978-0-521-15175-7. [Google Scholar]
- Morel, A.; Bricaud, A. Theoretical results concerning light absorption in a discrete medium, and application to specific absorption of phytoplankton. Deep Sea Res. Part A Oceanogr. Res. Pap. 1981, 28, 1375–1393. [Google Scholar] [CrossRef]
- Chisholm, S.W. Phytoplankton size. In Primary Productivity and Biogeochemical Cycles in the Sea; Springer: New York, NY, USA, 1992. [Google Scholar]
- Roy, S.; Llewellyn, C.A.; Egeland, E.S.; Johnsen, G. Phytoplankton Pigments: Characterization, Chemotaxonomy and Applications in Oceanography; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Jeffrey, S.; Mantoura, R.; Wright, S. Phytoplankton Pigments in Oceanography: Guidelines to Modern Methods; Unesco Publishing: Paris, France, 1997; ISBN 92-3-103275-5. [Google Scholar]
- Vidussi, F.; Claustre, H.; Manca, B.B.; Luchetta, A.; Marty, J.C. Phytoplankton pigment distribution in relation to upper thermocline circulation in the eastern Mediterranean Sea during winter. J. Geophys. Res. Oceans 2001, 106, 19939–19956. [Google Scholar] [CrossRef] [Green Version]
- Uitz, J.; Claustre, H.; Morel, A.; Hooker, S.B. Vertical distribution of phytoplankton communities in Open Ocean: An assessment based on surface chlorophyll. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]
- Hood, R.R.; Laws, E.A.; Armstrong, R.A.; Bates, N.R.; Brown, C.W.; Carlson, C.A.; Chai, F.; Doney, S.C.; Falkowski, P.G.; Feely, R.A. Pelagic functional group modeling: Progress, challenges and prospects. Deep Sea. Res. Part II Top. Stud. Oceanogr. 2006, 53, 459–512. [Google Scholar] [CrossRef] [Green Version]
- Quere, C.L.; Harrison, S.P.; Colin Prentice, I.; Buitenhuis, E.T.; Aumont, O.; Bopp, L.; Claustre, H.; Cotrim Da Cunha, L.; Geider, R.; Giraud, X. Ecosystem dynamics based on plankton functional types for global ocean biogeochemistry models. Glob. Chang. Biol. 2005, 11, 2016–2040. [Google Scholar] [CrossRef]
- Moloney, C.L.; Field, J.G. The size-based dynamics of plankton food webs. I. A simulation model of carbon and nitrogen flows. J. Geophys. Res. 1991, 13, 1003–1038. [Google Scholar] [CrossRef]
- Marinov, I.; Doney, S.C.; Lima, I.D. Response of ocean phytoplankton community structure to climate change over the 21st century: Partitioning the effects of nutrients, temperature and light. Biogeosciences 2010, 7, 3941–3959. [Google Scholar] [CrossRef]
- Sathyendranath, S.; Cota, G.; Stuart, V.; Maass, H.; Platt, T. Remote sensing of phytoplankton pigments: A comparison of empirical and theoretical approaches. Int. J. Remote Sens. 2001, 22, 249–273. [Google Scholar] [CrossRef]
- Kostadinov, T.S.; Siegel, D.A.; Maritorena, S. Retrieval of the particle size distribution from satellite ocean color observations. J. Geophys. Res. 2009, 114. [Google Scholar] [CrossRef] [Green Version]
- Loisel, H.; Nicolas, J.M.; Sciandra, A.; Stramski, D.; Poteau, A. Spectral dependency of optical backscattering by marine particles from satellite remote sensing of the global ocean. J. Geophys. Res. Oceans 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Sathyendranath, S.; Lazzara, L.; Prieur, L. Variations in the spectral values of specific absorption of phytoplankton. Limnol. Oceanogr. 1987, 32, 403–415. [Google Scholar] [CrossRef] [Green Version]
- Reynolds, R.A.; Stramski, D.; Mitchell, B.G. A chlorophyll-dependent semianalytical reflectance model derived from field measurements of absorption and backscattering coefficients within the southern ocean. J. Geophys. Res. Oceans 2001, 106, 7125–7138. [Google Scholar] [CrossRef]
- Alvain, S.; Moulin, C.; Dandonneau, Y.; Bréon, F.M. Remote sensing of phytoplankton groups in case 1 waters from global seawifs imagery. Deep Sea Res. Part I Oceanogr. Res. Pap. 2005, 52, 1989–2004. [Google Scholar] [CrossRef] [Green Version]
- Devred, E.; Sathyendranath, S.; Stuart, V.; Platt, T. A three component classification of phytoplankton absorption spectra: Application to ocean-color data. Remote Sens. Environ. 2011, 115, 2255–2266. [Google Scholar] [CrossRef]
- Devred, E.; Sathyendranath, S.; Stuart, V.; Maass, H.; Ulloa, O.; Platt, T. A two-component model of phytoplankton absorption in the open ocean: Theory and applications. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef] [Green Version]
- Bricaud, A. Natural variability of phytoplanktonic absorption in oceanic waters: Influence of the size structure of algal populations. J. Geophys. Res. 2004, 109. [Google Scholar] [CrossRef] [Green Version]
- Barnes, C.; Irigoien, X.; De Oliveira, J.A.; Maxwell, D.; Jennings, S. Predicting marine phytoplankton community size structure from empirical relationships with remotely sensed variables. J. Plankton Res. 2011, 33, 13–24. [Google Scholar] [CrossRef]
- Palacz, A.P.; John, M.A.S.; Brewin, R.J.W.; Hirata, T.; Gregg, W.W. Distribution of phytoplankton functional types in high-nitrate low-chlorophyll waters in a new diagnostic ecological indicator model. Biogeosci. Discuss. 2013, 10, 8103–8157. [Google Scholar] [CrossRef] [Green Version]
- Brewin, R.J.W.; Hardman-Mountford, N.J.; Lavender, S.J.; Raitsos, D.E.; Hirata, T.; Uitz, J.; Devred, E.; Bricaud, A.; Ciotti, A.; Gentili, B. An intercomparison of bio-optical techniques for detecting dominant phytoplankton size class from satellite remote sensing. Remote Sens. Environ. 2011, 115, 325–339. [Google Scholar] [CrossRef]
- Di Cicco, A.; Sammartino, M.; Marullo, S.; Santoleri, R. Regional empirical algorithms for an improved identification of phytoplankton functional types and size classes in the mediterranean sea using satellite data. Front. Mar. Sci. 2017, 4, 126. [Google Scholar] [CrossRef]
- Kostadinov, T.S.; Cabré, A.; Vedantham, H.; Marinov, I.; Bracher, A.; Brewin, R.J.; Bricaud, A.; Hirata, T.; Hirawake, T.; Hardman-Mountford, N.J. Inter-comparison of phytoplankton functional type phenology metrics derived from ocean color algorithms and earth system models. Remote Sens. Environ. 2017, 190, 162–177. [Google Scholar] [CrossRef]
- Longhurst, A. The Atlantic Ocean; Elsevier Science Publishers: New York, NY, USA, 2006; pp. 131–268. ISBN 978-0-12-455521-1. [Google Scholar]
- Devred, E.; Sathyendranath, S.; Platt, T. Delineation of ecological provinces using ocean colour radiometry. Mar. Ecol. Prog. Ser. 2007, 346, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Department of Fisheries and Oceans (DFO). Optical, Chemical, and Biological Oceanographic Conditions on the Scotian Shelf and in the Eastern Gulf of Maine in 2015; Fishery and Oceans Canada: Ottawa, Canada, 2017. [Google Scholar]
- Yentsch, C.S. Measurement of visible light absorption by particulate matter in the ocean. Limnol. Oceanogr. 1962, 7, 207–217. [Google Scholar] [CrossRef] [Green Version]
- Mitchell, B.; Kiefer, D. Determination of absorption and fluorescence excitation spectra for phytoplankton. In Marine Phytoplankton and Productivity; Springer: Berlin/Heidelberg, Germany, 1984; pp. 157–169. [Google Scholar]
- Hoepffner, N.; Sathyendranath, S. Effect of pigment composition on absorption properties of phytoplankton. Mar. Ecol. Prog. Ser. 1991, 73, 11–23. [Google Scholar] [CrossRef]
- Kyewalyanga, M.N.; Platt, T.; Sathyendranath, S. Estimation of the photosynthetic action spectrum: Implication for primary production models. Mar. Ecol. Prog. Ser. 1997, 146, 207–223. [Google Scholar] [CrossRef]
- Stuart, V.; Head, E.J. The Second Seawifs Hplc Analysis Round-Robin Experiment (Seaharre-2) (p. 112); NASA/TM: Greenbelt, MD, USA, 2005; p. 124. [Google Scholar]
- Craig, S.E.; Jones, C.T.; Li, W.K.W.; Lazin, G.; Horne, E.; Caverhill, C.; Cullen, J.J. Deriving optical metrics of coastal phytoplankton biomass from ocean colour. Remote Sens. Environ. 2012, 119, 72–83. [Google Scholar] [CrossRef]
- Lee, Z.; Carder, K.L.; Arnone, R.A. Deriving inherent optical properties from water color: A multiband quasi-analytical algorithm for optically deep waters. Appl. Opt. 2002, 41, 5755–5772. [Google Scholar] [CrossRef] [PubMed]
- Belo Couto, A.; Brotas, V.; Mélin, F.; Groom, S.; Sathyendranath, S. Inter-comparison of oc-cci chlorophyll-a estimates with precursor data sets. Int. J. Remote Sens. 2016, 37, 4337–4355. [Google Scholar] [CrossRef]
- Swift, J.H. The arctic waters. In The Nordic Seas; Springer: Berlin/Heidelberg, Germany, 1986; pp. 129–154. [Google Scholar]
- Hirata, T.; Aiken, J.; Hardman-Mountford, N.; Smyth, T.J.; Barlow, R.G. An absorption model to determine phytoplankton size classes from satellite ocean colour. Remote Sens. Environ. 2008, 112, 3153–3159. [Google Scholar] [CrossRef]
- Brewin, R.J.W.; Sathyendranath, S.; Hirata, T.; Lavender, S.J.; Barciela, R.M.; Hardman-Mountford, N.J. A three-component model of phytoplankton size class for the Atlantic Ocean. Ecol. Model. 2010, 221, 1472–1483. [Google Scholar] [CrossRef]
- Claustre, H.; Hooker, S.B.; Van Heukelem, L.; Berthon, J.-F.; Barlow, R.; Ras, J.; Sessions, H.; Targa, C.; Thomas, C.S.; van der Linde, D.; et al. An intercomparison of hplc phytoplankton pigment methods using in situ samples: Application to remote sensing and database activities. Mar. Chem. 2004, 85, 41–61. [Google Scholar] [CrossRef]
- Shanmugam, P.; Ahn, Y.-H.; Ryu, J.-H.; Sundarabalan, B. An evaluation of inversion models for retrieval of inherent optical properties from ocean color in coastal and open sea waters around Korea. J. Oceanogr. 2010, 66, 815–830. [Google Scholar] [CrossRef]
- Partensky, F.; Hoepffner, N.; Li, W.K.; Ulloa, O.; Vaulot, D. Photoacclimation of Prochlorococcus sp. (prochlorophyta) strains isolated from the North Atlantic and the Mediterranean Sea. Plant Physiol. 1993, 101, 285–296. [Google Scholar] [CrossRef] [PubMed]
- Moore, L. Comparative physiology of synechococcus and prochlorococcus: Influence of light and temperature on growth, pigments, fluorescence and absorptive properties. Mar. Ecol. Prog. Ser. 1995, 116, 259–275. [Google Scholar] [CrossRef]
- Jeffrey, S. A report of green algal pigments in the central North Pacific Ocean. Mar. Biol. 1976, 37, 33–37. [Google Scholar] [CrossRef]
- Simon, N.; Barlow, R.G.; Marie, D.; Partensky, F.; Vaulot, D. Characterization of oceanic photosynthetic picoeukaryotes by flow cytometry. J. Phycol. 1994, 30, 922–935. [Google Scholar] [CrossRef]
- Gonzalez Taboada, F.; Anadon, R. Seasonality of north Atlantic phytoplankton from space: Impact of environmental forcing on a changing phenology (1998–2012). Glob. Chang. Biol. 2014, 20, 698–712. [Google Scholar] [CrossRef] [PubMed]
- Department of Fisheries and Oceans (DFO). Oceanographic Conditions in the Atlantic Zone in 2012; Fishery and Oceans Canada: Ottawa, Canada, 2013. [Google Scholar]
- Department of Fisheries and Oceans (DFO). Oceanographic Conditions in the Atlantic Zone in 2013; Fishery and Oceans Canada: Ottawa, Canada, 2014. [Google Scholar]
- Department of Fisheries and Oceans (DFO). Oceanographic Conditions in the Atlantic Zone in 2014; Fishery and Oceans Canada: Ottawa, Canada, 2015. [Google Scholar]
- Department of Fisheries and Oceans (DFO). Oceanographic Conditions in the Atlantic Zone in 2015; Fishery and Oceans Canada: Ottawa, Canada, 2016. [Google Scholar]
- Department of Fisheries and Oceans (DFO). Oceanographic Conditions in the Atlantic Zone in 2016; Fishery and Oceans Canada: Ottawa, Canada, 2017. [Google Scholar]
- Head, E.J.; Pepin, P. Spatial and inter-decadal variability in plankton abundance and composition in the northwest Atlantic (1958–2006). J. Plankton Res. 2010, 32, 1633–1648. [Google Scholar] [CrossRef]













| Dataset | Sensor/Source | Quantity | Usage |
|---|---|---|---|
| Coincident Rrs and in situ pigments a (Figure 1a) | SeaWiFS | 268 |
|
| MODIS | 644 | ||
| VIIRS | 319 | ||
| Coincident Rrs and in situ phytoplankton absorption (Figure 1b) | SeaWiFS | 138 | Evaluation of the IOP products |
| MODIS | 318 | ||
| VIIRS | 130 | ||
| Daily satellite image | OC-CCI v3.1 | 1998 to 2016 | Generate the PSC in NWA |
| Model | Reference | Type | Size Classes | Satellite Input Variables | |||
|---|---|---|---|---|---|---|---|
| Chla | aph(λ) 1 | aph(λ) 2 | SST | ||||
| A | Hirata et al. (2008) | Abundance-based | 3 | √ | |||
| B | Hirata et al. (2008) | Abundance-based | 3 | √ | |||
| C | Hirata et al. (2008) | Abundance-based | 3 | √ | |||
| D | Devred et al. (2006) | Abundance-based | 2 | √ | |||
| E | Devred et al. (2011) | Abundance-based | 3 | √ | |||
| F | Devred et al. (2011) | Spectral-based | 3 | √ | |||
| G | Devred et al. (2011) | Spectral-based | 3 | √ | |||
| H | Brewin et al. (2010) | Abundance-based | 3 | √ | |||
| I | Barnes et al. (2011) | Ecological-based | 3 | √ | √ | ||
| SeaWiFS | MODIS | VIIRS | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Dataset | Method | Micro % | Nano + Pico % | Nano % | Pico % | Micro % | Nano + Pico % | Nano % | Pico % | Micro % | Nano + Pico % | Nano % | Pico % |
| Northwest Atlantic | A | 24.2 ± 6.5 | 75.3 ± 7.4 | 94.8 ± 5.5 | 13.0 ± 12.9 | 21.2 ± 4.5 | 56.2 ± 4.8 | 75.1± 5.4 | 52.1 ± 8.2 | 40.8 ± 8.8 | 48 ± 6.2 | 69.3 ± 8.5 | 50 ± 8.6 |
| B | 17.5 ± 5.8 | 24.7 ± 7.3 | 46.0 ± 9.3 | 69.6 ± 19.4 | 1.0 ± 1.1 | 0.6 ± 0.7 | 0 | 90.7 ± 5.5 | 1 ± 1.8 | 0.42 ± 0.8 | 0 | 97.3 ± 4.1 | |
| C | 47.5 ± 7.7 | 69.3 ± 7.9 | 95.4 ± 5.3 | 52.2 ± 18.4 | 40.2 ± 5.5 | 71.4 ± 4.4 | 94.8 ± 3.5 | 24.6 ± 6.8 | 19.4 ± 7.0 | 76.8 ± 5.3 | 95.0 ± 5.0 | 30.4 ± 7.7 | |
| D | 80.6 ± 6.2 | 88.0 ± 5.7 | \ | \ | 74.0 ± 5.0 | 83.1 ±3.7 | \ | \ | 60.0 ± 8.8 | 89.4 ± 3.9 | \ | \ | |
| E | 83.1 ± 5.9 | 81.7 ± 6.7 | 0 | 52.2 ± 18.4 | 79.5 ± 4.6 | 78.0 ± 4.1 | 0 | 28.0 ± 7.0 | 70.1 ± 8.4 | 86.0 ± 4.4 | 0 | 30.0 ± 7.7 | |
| F | 86.6 ± 5.3 | 16.7 ± 6.4 | 21.3 ± 7.7 | 0 | 87.9 ± 3.8 | 40.0 ± 4.7 | 43.6 ± 6.1 | 0 | 89.1 ± 6.3 | 64.3 ± 6.0 | 69.8 ± 8.5 | 0 | |
| G | 55.7 ± 7.6 | 91.2 ± 5.0 | 3.4 ± 2.9 | 78.3 ± 18.3 | 52.8 ± 5.6 | 85.4 ± 3.5 | 0 | 57.2 ± 7.8 | 59.2 ± 9.0 | 96.2 ± 2.5 | 0 | 65.6 ± 8.3 | |
| H | 63.7 ± 7.5 | 94.4 ± 4.2 | 92.0 ± 6.2 | 30.4 ± 17.3 | 53.0 ± 5.6 | 94.4 ± 2.4 | 89.3 ± 4.2 | 11.4 ± 4.9 | 33.3 ± 8.2 | 99.2 ± 1.4 | 93.0 ± 5.5 | 13.0 ± 5.6 | |
| I | 0 | 100 ± 1.7 | 100 ± 3.9 | 47.8 ± 18.8 | 0 | 100.0 ± 0.9 | 100 ± 2.5 | 2.1 ± 1.9 | 0 | 100 ± 0.9 | 96.0 ± 4.7 | 21.4 ± 6.9 | |
| No. of samples | 165 | 121 | 81 | 14 | 305 | 403 | 187 | 133 | 110 | 240 | 87 | 122 | |
| Open Ocean (Brewin et al. 2011) | B | 36.5 ± 7.6 | 96 ± 1.8 | 22.1 ±5.4 | 93.1 ±3.2 | \ | \ | \ | \ | \ | \ | \ | \ |
| C | 90.1 ± 4.7 | 95.1 ± 1.9 | 37.1 ± 6.4 | 87.4 ±4.1 | \ | \ | \ | \ | \ | \ | \ | \ | |
| D | 91 ± 4.5 | 94 ± 2.1 | \ | \ | \ | \ | \ | \ | \ | \ | \ | \ | |
| No. of samples | 92 | 285 | 112 | 173 | \ | \ | \ | \ | \ | \ | \ | \ | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, X.; Devred, E.; Johnson, C. Remote Sensing of Phytoplankton Size Class in Northwest Atlantic from 1998 to 2016: Bio-Optical Algorithms Comparison and Application. Remote Sens. 2018, 10, 1028. https://doi.org/10.3390/rs10071028
Liu X, Devred E, Johnson C. Remote Sensing of Phytoplankton Size Class in Northwest Atlantic from 1998 to 2016: Bio-Optical Algorithms Comparison and Application. Remote Sensing. 2018; 10(7):1028. https://doi.org/10.3390/rs10071028
Chicago/Turabian StyleLiu, Xiaohan, Emmanuel Devred, and Catherine Johnson. 2018. "Remote Sensing of Phytoplankton Size Class in Northwest Atlantic from 1998 to 2016: Bio-Optical Algorithms Comparison and Application" Remote Sensing 10, no. 7: 1028. https://doi.org/10.3390/rs10071028
APA StyleLiu, X., Devred, E., & Johnson, C. (2018). Remote Sensing of Phytoplankton Size Class in Northwest Atlantic from 1998 to 2016: Bio-Optical Algorithms Comparison and Application. Remote Sensing, 10(7), 1028. https://doi.org/10.3390/rs10071028