Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model
Abstract
:1. Introduction
2. Methodology
2.1. GNSS SPP and RTD Mathematical Models
2.2. A Real-Time Adaptive Weighting Model
3. Data and Experiments
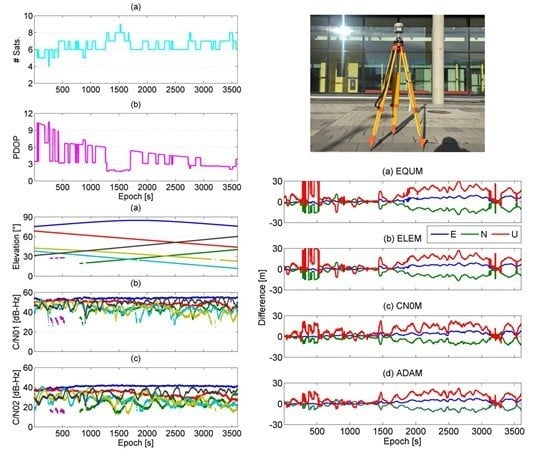
4. Results and Discussion
4.1. Template Functions
4.2. Static Experiment Near Buildings
4.3. Static Experiment Near Trees
4.4. Kinematic Experiment
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Li, T.; Zhang, H.; Gao, Z.; Chen, Q.; Niu, X. High-accuracy positioning in urban environments using single-frequency multi-GNSS RTK/MEMS-IMU integration. Remote Sens. 2018, 10, 205. [Google Scholar] [CrossRef]
- Cai, C.; Pan, L.; Gao, Y. A precise weighting approach with application to combined L1/B1 GPS/BeiDou positioning. J. Navig. 2014, 67, 911–925. [Google Scholar] [CrossRef]
- Hsu, L.; Jan, S.; Groves, P.; Kubo, N. Multipath mitigation and NLOS detection using vector tracking in urban environments. GPS Solut. 2015, 19, 249–262. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Shen, Y. Comparison and analysis of unmodelled errors in GPS and BeiDou signals. Geodesy Geodyn. 2017, 8, 41–48. [Google Scholar] [CrossRef]
- Li, B.; Zhang, Z.; Shen, Y.; Yang, L. A procedure for the significance testing of unmodeled errors in GNSS observations. J. Geodesy 2018, 1–16. [Google Scholar] [CrossRef]
- Pietrantonio, G.; Riguzzi, F. Three-dimensional strain tensor estimation by GPS observations: Methodological aspects and geophysical applications. J. Geodyn. 2004, 38, 1–18. [Google Scholar] [CrossRef]
- Shu, Y.; Fang, R.; Liu, J. Stochastic Models of Very High-Rate (50 Hz) GPS/BeiDou Code and Phase Observations. Remote Sens. 2017, 9, 1188. [Google Scholar] [Green Version]
- Koch, K. Parameter Estimation and Hypothesis Testing in Linear Models; Springer: Berlin, Germany, 1999. [Google Scholar]
- Li, B.; Shen, Y.; Lou, L. Efficient estimation of variance and covariance components: A case study for GPS stochastic model evaluation. Geosci. Remote Sens. IEEE Trans. 2011, 49, 203–210. [Google Scholar] [CrossRef]
- Baarda, W. A Testing Procedure for Use in Geodetic Networks; Rijkscommissie voor Geodesie: Kanaalweg 4, Delft, The Netherlands, 1968. [Google Scholar]
- Teunissen, P. Testing Theory: An Introduction; VSSD: Delft, The Netherlands, 2000. [Google Scholar]
- Bischoff, W.; Heck, B.; Howind, J.; Teusch, A. A procedure for testing the assumption of homoscedasticity in least squares residuals: A case study of GPS carrier-phase observations. J. Geodesy 2005, 78, 397–404. [Google Scholar] [CrossRef]
- Euler, H.; Goad, C. On optimal filtering of GPS dual frequency observations without using orbit information. Bull. Géodésique 1991, 65, 130–143. [Google Scholar] [CrossRef]
- King, R.; Bock, Y. Documentation for the GAMIT GPS Analysis Software; Massachusetts Institute of Technology: Cambridge, MA, USA, 2000; Available online: http://www-gpsg.mit.edu/~simon/gtgk/GAMIT.pdf (accessed on 24 June 2018).
- Dach, R.; Hugentobler, U.; Fridez, P.; Meindl, M. Bernese GPS Software, version 5.0; Astronomical Institute, University of Bern: Bern, Switzerland, 2007. [Google Scholar]
- Amiri-Simkooei, A.; Teunissen, P.; Tiberius, C. Application of least-squares variance component estimation to GPS observables. J. Surv. Eng. 2009, 135, 149–160. [Google Scholar] [CrossRef]
- Li, B.; Zhang, L.; Verhagen, S. Impacts of BeiDou stochastic model on reliability: Overall test, w-test and minimal detectable bias. GPS Solut. 2017, 21, 1095–1112. [Google Scholar] [CrossRef]
- Axelrad, P.; Comp, C.; Macdoran, P.F. SNR-based multipath error correction for GPS differential phase. IEEE Trans. Aerosp. Electron. Syst. 1996, 32, 650–660. [Google Scholar] [CrossRef]
- Bilich, A.; Larson, K. Mapping the GPS multipath environment using the signal-to-noise ratio (SNR). Radio Sci. 2007, 43, 3442–3446. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. A new signal-to-noise-ratio based stochastic model for GNSS high-precision carrier phase data processing algorithms in the presence of multipath errors. In Proceedings of the ION GNSS 2006, Fort Worth, TX, USA, 26–29 September 2006; pp. 276–285. [Google Scholar]
- Talbot, N. Optimal weighting of GPS carrier phase observations based on the signal-to-noise ratio. In Proceedings of the International Symposia on Global Positioning Systems, Gold Coast, Queensland, Australia, 17–19 October 1998. [Google Scholar]
- Brunner, F.; Hartinger, H.; Troyer, L. GPS signal diffraction modelling: The stochastic SIGMA-Δ model. J. Geodesy 1999, 73, 259–267. [Google Scholar] [CrossRef]
- Hartinger, H.; Brunner, F. Variances of GPS phase observations: The SIGMA-ε model. GPS Solut. 1999, 2, 35–43. [Google Scholar] [CrossRef]
- Wieser, A.; Brunner, F. An extended weight model for GPS phase observations. Earth Planets Space 2000, 52, 777–782. [Google Scholar] [CrossRef] [Green Version]
- de Bakker, P.; Tiberius, C.; van der Marel, H.; van Bree, R. Short and zero baseline analysis of GPS L1 C/A, L5Q, GIOVE E1B, and E5aQ signals. GPS Solut. 2012, 16, 53–64. [Google Scholar] [CrossRef]
- Li, B. Stochastic modeling of triple-frequency BeiDou signals: Estimation, assessment and impact analysis. J. Geodesy 2016, 90, 593–610. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, B.; Shen, Y.; Yang, L. A noise analysis method for GNSS signals of a standalone receiver. Acta Geod. Geophys. 2017, 52, 301–316. [Google Scholar] [CrossRef]
- Luo, X.; Mayer, M.; Heck, B.; Awange, J. A Realistic and Easy-to-Implement Weighting Model for GPS Phase Observations. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6110–6118. [Google Scholar] [CrossRef]
- Yu, W.; Chen, B.; Dai, W.; Luo, X. Real-Time Precise Point Positioning Using Tomographic Wet Refractivity Fields. Remote Sens. 2018, 10, 928. [Google Scholar] [CrossRef]
- Comp, C.; Axelrad, P. Adaptive SNR-based carrier phase multipath mitigation technique. IEEE Trans. Aerosp. Electron. Syst. 1998, 34, 264–276. [Google Scholar] [CrossRef]
- Braasch, M. Multipath. In Springer Handbook of Global Navigation Satellite Systems; Springer: Berlin, Germany, 2017; pp. 443–468. [Google Scholar]
- Bilich, A.; Larson, K.; Axelrad, P. Modeling GPS phase multipath with SNR: Case study from the Salar de Uyuni, Boliva. J. Geophys. Res. Solid Earth 2008, 113. [Google Scholar] [CrossRef] [Green Version]
- Groves, P.; Jiang, Z.; Rudi, M.; Strode, P. A Portfolio Approach to NLOS and Multipath Mitigation in Dense Urban Areas. In Proceedings of the 26th International Technical Meeting of the Satellite Division of the Institute of Navigation (ION GNSS+ 2013), Nashville, TN, USA, 16–20 September 2013; pp. 3231–3247. [Google Scholar]
- Strode, P.; Groves, P. GNSS multipath detection using three-frequency signal-to-noise measurements. GPS Solut. 2016, 20, 399–412. [Google Scholar] [CrossRef]
- Lau, L.; Cross, P. Development and testing of a new ray-tracing approach to GNSS carrier-phase multipath modelling. J. Geodesy 2007, 81, 713–732. [Google Scholar] [CrossRef]
- Moradi, R.; Schuster, W.; Feng, S.; Jokinen, A.; Ochieng, W. The carrier-multipath observable: A new carrier-phase multipath mitigation technique. GPS Solut. 2014, 19, 73–82. [Google Scholar] [CrossRef]
- Kaplan, E.; Hegarty, C. Understanding GPS: Principles and Applications; Artech House: Norwood, MA, USA, 2006. [Google Scholar]
- Misra, P.; Enge, P. Global Positioning System: Signals, Measurements, and Performance; Ganga-Jamuna Press: Lincoln, MA, USA, 2012. [Google Scholar]
- Klobuchar, J. Ionospheric time-delay algorithm for single-frequency GPS users. IEEE Trans. Aerosp. Electron. Syst. 1987, 325–331. [Google Scholar] [CrossRef]
- Hopfield, H. Two-quartic tropospheric refractivity profile for correcting satellite data. J. Geophys. Res. Atmos. 1969, 74, 4487–4499. [Google Scholar] [CrossRef]
- Odijk, D. Weighting ionospheric corrections to improve fast GPS positioning over medium distances. In Proceedings of the ION GPS, Salt Lake City, UT, USA, 19–22 September 2000; pp. 1113–1123. [Google Scholar]
- Lau, L.; Cross, P. Investigations into phase multipath mitigation techniques for high precision positioning in difficult environments. J. Navig. 2007, 60, 457–482. [Google Scholar] [CrossRef]
- Bona, P. Precision, cross correlation, and time correlation of GPS phase and code observations. GPS Solut. 2000, 4, 3–13. [Google Scholar] [CrossRef]
- Dow, J.; Neilan, R.; Rizos, C. The international GNSS service in a changing landscape of global navigation satellite systems. J. Geodesy 2009, 83, 191–198. [Google Scholar] [CrossRef]

















| SPP | RTD | |||||||
|---|---|---|---|---|---|---|---|---|
| EQUM | ELEM | CN0M | ADAM | EQUM | ELEM | CN0M | ADAM | |
| E | 11.73 | 11.35 | 11.79 | 11.15 | 4.36 | 4.19 | 3.83 | 3.59 |
| N | 22.44 | 18.43 | 12.37 | 10.74 | 8.69 | 7.63 | 6.00 | 5.91 |
| U | 36.03 | 30.74 | 18.99 | 15.65 | 14.92 | 13.43 | 11.57 | 10.84 |
| 3D | 44.04 | 37.59 | 25.55 | 22.01 | 17.81 | 16.00 | 13.58 | 12.86 |
| SPP | RTD | |||||||
|---|---|---|---|---|---|---|---|---|
| EQUM | ELEM | CN0M | ADAM | EQUM | ELEM | CN0M | ADAM | |
| E | 3.20 | 3.18 | 3.02 | 3.01 | 0.41 | 0.43 | 0.38 | 0.38 |
| N | 3.97 | 3.64 | 3.69 | 3.49 | 0.65 | 0.62 | 0.58 | 0.62 |
| U | 5.08 | 3.93 | 4.36 | 3.60 | 2.32 | 2.01 | 2.23 | 1.90 |
| 3D | 7.20 | 6.23 | 6.46 | 5.85 | 2.44 | 2.15 | 2.34 | 2.03 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Li, B.; Shen, Y.; Gao, Y.; Wang, M. Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model. Remote Sens. 2018, 10, 1157. https://doi.org/10.3390/rs10071157
Zhang Z, Li B, Shen Y, Gao Y, Wang M. Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model. Remote Sensing. 2018; 10(7):1157. https://doi.org/10.3390/rs10071157
Chicago/Turabian StyleZhang, Zhetao, Bofeng Li, Yunzhong Shen, Yang Gao, and Miaomiao Wang. 2018. "Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model" Remote Sensing 10, no. 7: 1157. https://doi.org/10.3390/rs10071157
APA StyleZhang, Z., Li, B., Shen, Y., Gao, Y., & Wang, M. (2018). Site-Specific Unmodeled Error Mitigation for GNSS Positioning in Urban Environments Using a Real-Time Adaptive Weighting Model. Remote Sensing, 10(7), 1157. https://doi.org/10.3390/rs10071157