An Improved BDS Satellite-Induced Code Bias Correction Model Considering the Consistency of Multipath Combinations

Abstract

The satellite-induced systematic biases were identified to exist in the code observations from BeiDou navigation satellite system (BDS) satellites using multipath (MP) combinations. The current correction model for satellite-induced code bias (SICB) does not take into account the consistency of MP combinations, which limits the accuracy of the developed model. Both the cycle slips and different tracking of a satellite at different stations can affect the absolute values of MP combinations, although the variations remain unchanged. An improved SICB piecewise linear correction model as a function of elevations is proposed. We estimate the model parameters for each frequency and for each satellite. The single-difference of MP combinations in the domain of elevation angles is carried out to remove the unknown ambiguities and stable hardware delays so that the SICB modeling is free of the effects of MP combination inconsistency. In addition, a denser elevation node separation of 1°, rather than the 10° usually employed by the traditional model, is used to describe the more precise SICB variations. The SICB corrections show significant differences among orbit types and frequency bands. The SICB variations have much less effect on Inclined Geosynchronous Orbit (IGSO) satellites than on Medium Earth Orbit (MEO) satellites for the regional BDS (BDS-2). The B1 signal has the largest SICB corrections, which can be up to 0.9 m close to zenith for BDS-2 MEO satellites, and the B2 signal follows. After adding the SICB corrections to the code observations, the elevation-dependent code biases vanish, and we can obtain improved code observations. After applying the improved SICB correction model, the root mean square (RMS) values of MP combination time series are reduced by 7%, 6% and 2%, and 18%, 14% and 5% on the B1, B2 and B3 frequencies for the BDS-2 IGSO and MEO satellites, respectively. For comparison, we also establish the traditional SICB correction model. With the traditional SICB correction model, the corresponding RMS MP combinations are smaller than those of uncorrected MP series, but slightly larger than those of corrected MP series using the improved SICB correction model. To validate the effectiveness and correctness of our proposed model, single-frequency precise point positioning (PPP) processing with BDS-2 MEO and IGSO satellites is conducted. An accuracy improvement of 24%, 19% and 89%, and 7%, 7% and 6% for the single-frequency PPP applying the improved SICB corrections over the case without SICB corrections and the case using the traditional SICB corrections in east, north and vertical directions is achieved, respectively. Although only centimeter-level SICB variations could be observed for the two legacy signals B1 and B3 and the three new navigation signals B1C, B2a and B2b transmitted by the satellites of global BDS demonstration system (BDS-3S), we still establish an effective SICB correction model on the B1 and B3 frequencies for BDS-3S IGSO satellites, and the RMS MP combinations are reduced by 1–4% after applying the improved SICB corrections.

1. Introduction

As one of the Global Navigation Satellite Systems (GNSSs), the BeiDou navigation satellite system (BDS) has been a relevant and valuable complement for establishing improved positioning, navigation and timing (PNT) services. The regional BDS (BDS-2) has been providing stable and continuous PNT services for customers in the Asia-Pacific region since 27 December 2012. Currently, the BDS-2 constellation consists of six geostationary orbit (GEO) satellites (C01–C05, C17), six inclined geosynchronous orbit (IGSO) satellites (C06–C10, C15/C13), and three medium earth orbit (MEO) satellites (C11, C12, C14). At present, the BDS-2 GEO satellite C17 has still not been put into use. All BDS-2 satellites are able to provide B1, B2 and B3 signals with a center frequency of 1561.098, 1207.14 and 1268.52 MHz, respectively [1].

The BDS implementation has been performed in three steps in terms of its deployment timeline: BeiDou navigation demonstration system (BDS-1) by 2000, BDS-2 by 2012 and global BDS (BDS-3) by 2020. Following the “three-step” strategy, the BDS-3 is under construction. The constellation deployment of BDS-3 is expected to be completed by 2020, and the enhanced PNT services will be able to be provided to the global users at that time. The full constellation of BDS-3 will be composed of five GEO satellites, three IGSO satellites and 27 MEO satellites. As of 29 March 2018, a total of eight BDS-3 satellites (C19–C22, C27–C30) have been launched. All these satellites are currently unavailable because they are still in the phase of flight tests. A BDS-3 demonstration system (BDS-3S) was established before the launch of the first BDS-3 satellite, including three MEO satellites (C33–C35) and two IGSO satellites (C31, C32). The BDS-3S satellite C35 was launched on 1 February 2016, but its antenna failed to transmit navigation signals. The BDS-3S is used to validate the design of BDS-3, including inter-satellite links, new hydrogen clock and complex ranging signals. All the BDS-3S satellites, except C31, are capable of transmitting three new navigation signals, namely, B1C centered at 1575.42 MHz, B2a at 1176.45 MHz, and B2b at 1207.14 MHz, which overlap with Galileo E1/E5a/E5b and GPS L1/L5 signals so as to enhance the compatibility and interoperability with other GNSS systems. In addition, all these satellites, including C31, can also broadcast signals on the two legacy frequencies B1 and B3 to ensure that the BDS-2 can be smoothly transited to BDS-3 [2].

With the signal transmission of BDS-2 satellite M1, a new type of systematic biases existing in code observations was identified [3]. As for other BDS-2 satellites, Montenbruck et al. [4] also observed the systematic code biases. Wanninger and Beer [5] provided more details. They concluded that the code biases with a varying range of approximately 1 m from horizon to zenith were both frequency- and elevation-dependent. They also found significant differences between code bias variations of IGSO-type and MEO-type satellites. In addition, the systematic code biases should be attributed to the transmitting satellites, because they were not dependent on the station location or receiver type. Therefore, the bias is termed satellite-induced code bias (SICB) in this study. The mechanism of SICB has now been identified clearly, and the root cause is the spacecraft internal multipath. The impedance mismatch between antenna elements and power divider network causes reflection signals. The downlink antenna retransmits the reflection signals. At the satellite end, the inner reflection signals depend on the bore-sight angles. Consequently, the elevation-dependent multipath errors can be observed at the user end [6].

Figure 1 shows the principle of multipath. The objects near the receiver will reflect the direct signals, and thus the reflected signals are generated. The reflected signals go through a longer path than the direct signals, which causes the large propagation delay. The received signals are the superposition of the direct and the reflected signals. The magnitude of the multipath errors is related to the distance between the antenna and the object, the angle of the reflected signal, and the characteristics of the reflector [7]. The principle of SICB is similar, but the reflection occurs at the satellite ends.

In order to mitigate or even eliminate the effects of SICB, a piecewise linear correction model for each frequency of BDS-2 IGSO-type and MEO-type satellites based on the trends of SICB against satellite elevation angles was proposed by Wanninger and Beer [5]. The SICB correction model was stable over time. After adding the correction values to the original code observations, the elevation-dependent SICB variations almost disappeared. Many researchers have focused on the refinement of this SICB correction model since then. To reduce the number of correction parameters, a correction model based on third-order polynomial fitting was developed by Lou et al. [8]. The SICB correction values were produced together with their stochastic information by Guo et al. [9], and the stochastic information can be used as precision indexes to refine the stochastic models of code measurements. According to Zou et al. [10] and Fu et al. [11], it was found that there existed obvious differences with respect to SICB variations against elevations for satellites with the same orbit type. Thus, they improved the correction model by estimating the correction values for each BDS-2 satellite, rather than IGSO-type or MEO-type satellites. All the above SICB correction models were established using the multipath (MP) combinations over all continuous ambiguity blocks. However, the MP combination inconsistency in terms of its absolute value, which is caused by the cycle slips and different tracking of a satellite at different stations, was ignored during the modeling process. In addition, the detailed SICB variations with elevation angles were vanished when using the piecewise linear fitting with a node separation of 5° or 10°, or especially the polynomial fitting. Due to the negative effects of the above two flaws, the accuracy of the current SICB correction model needs to be further improved.

The precise applications using the code measurements will be severely affected by the SICB. Many efforts have been made to investigate the benefits from SICB correction model. After applying the SICB correction values, an accuracy improvement of larger than 80% in the vertical direction could be achieved for the single-frequency precise point positioning (PPP) with BDS-2 IGSO and MEO satellites [12]. With the careful SICB consideration, the three-dimensional (3D) accuracy of overlapping orbits was improved from 11.0 and 14.0 cm to 6.9 and 10.5 cm for the BDS-2 MEO and IGSO satellites, respectively [13]. The precise correction of SICB resulted in a significant improvement of larger than 75% for wide-lane uncalibrated phase delay (UPD) estimation and a minor improvement of less than 25% for narrow-lane UPD estimation with respect to the PPP ambiguity resolution [14]. The long-term stability of differential code bias (DCB) for BDS-2 MEO satellites was improved by 12–28% after the SICB was corrected [15]. In this contribution, the single-frequency PPP is also used to verify our proposed SICB correction model.

The code observations from BDS-2 GEO satellites also suffer from the SICB effects. Following Lou et al. [8], the SICB variations of BDS-2 GEO satellites could be roughly corrected by the SICB correction model of BDS-2 IGSO satellites. However, the SICB correction for BDS-2 GEO satellites plays a limited role in improving the ambiguity-float PPP performance because the elevation angles of these satellites are almost constant. In addition, the code observations of BDS-2 GEO satellites are severely biased by ground multipath effects with an amplitude of 1–2 m, which are caused by ground-reflected satellite signals. Wang et al. [16] developed a method similar to the concept of sidereal filtering to remove both the SICB and ground multipath effects, and the feasibility of this method was verified by the improved position solutions. However, the correction values can only be obtained station-by-station. In other words, this method is station dependent, which limits its application. Therefore, BDS-2 GEO satellites are excluded from our SICB modeling analysis.

Since obvious SICB variations were identified for BDS-2 satellites, many studies have focused on the SICB for BDS-3S satellites since their real tracking data became available [6,17,18,19]. It was concluded that the marginal SICB variations might be negligible for the two legacy signals, as well as the three new navigation signals of all available BDS-3S satellites. The reason for the remarkable SICB mitigation is that the voltage standing-wave ratios of power divider networks are cut down for the BDS-3S satellites [6]. All the above results were obtained based on all-in-view antennas, the code observations that suffered from the severe ground multipath effects. SICB variations with a small size could be easily concealed. To gain more insight into the SICB of BDS-3S satellites, a 40-m dish antenna was used for analysis by Zhou et al. [20], so that the negative effects of the ground multipath errors can be removed. The results indicated that SICB variations with a level of about 0.1 m still existed for BDS-3S satellites. Most importantly, strong elevation-dependent SICB variations were still observed for the code observations from BDS-3S IGSO satellites on B1 and B3 frequencies. Therefore, an effective SICB correction model for the legacy signals of BDS-3S IGSO satellites should be established.

In this study, an improved SICB piecewise linear correction model is proposed, taking into account the consistency of MP combinations. We use a denser elevation node separation of 1° to describe more precise SICB variations so that our correction model can also be applied to BDS-3S satellites with much smaller SICB variations. We start with the modeling method for the SICB (Section 2). Subsequently, we show and analyze our results (Section 3). Finally, the conclusions are provided (Section 4).

2. Elevation-Dependent Modeling of Satellite-Induced Code Bias

2.1. Formulation of MP Combinations

Following the standard BDS measurement model, the code observations and the carrier phase observations on the ith frequency can be modeled as:

$$P_i=\rho +c\mathrm{d}{t}_r-c\mathrm{d}t+I\cdot {\gamma }_i+T+{\mu }_{r,i}+{\mu }_i+M_i+{\epsilon }_i+{\beta }_i$$

(1)

$$L_i=\rho +c\mathrm{d}{t}_r-c\mathrm{d}t-I\cdot {\gamma }_i+T+N_i+b_{r,i}+b_i+m_i+{\xi }_i$$

(2)

with ${\gamma }_i=f_1^2/f_i^2$, where P is the measured pseudorange, L is the measured carrier phase, ρ is the geometric distance between the phase centers of the receiver and the satellite antennas, cdt_r is the receiver clock offset, cdt is the satellite clock offset, I is the slant ionospheric delay on the B1 frequency, γ is the ionospheric delay factor with respect to the I, f is the signal frequency, T is the tropospheric path delay, N is the integer phase ambiguity, μ_r and μ are the receiver- and satellite-dependent code hardware delays, respectively, b_r and b are the phase hardware delays at the receiver and satellite ends, respectively, M and m are the multipath effects in the pseudorange and carrier phase observations, respectively, ε and ξ are the receiver code and phase measurement noises, respectively, and β is the elevation-dependent SICB in BDS code observations, which is the focus of this study.

In order to analyze the SICB β, the effects of the other terms shown in Equation (1) should be eliminated as much as possible. The linear combination of the code and carrier phase observations is an effective way to remove the common terms in the code and carrier phase observation equations, namely, Equations (1) and (2). The frequency-independent terms, including the geometric distance, receiver clock offset, satellite clock offset and the tropospheric delay, can be removed when the sum of the combination coefficients is equal to zero. In addition, the frequency-dependent ionospheric delay can also be removed by forming the ionospheric-free combination based on its dispersive nature. According to the above statements, we actually need a geometry-free and ionospheric-free (GFIF) combination. In addition, the GFIF combination should only involve the code observations on a single frequency so that we can model the SICB for each frequency. The MP combination, which is usually used to analyze the characteristics of GNSS code observations, is an optimal case for the required GFIF combination. The dual-frequency carrier phase observations and single-frequency code observations can be used to form the MP combinations. The MP combinations for the code observations on the ith frequency can be described as shown below [21]:

$$\begin{array}{ll}{\mathrm{MP}}_i& =P_i+(a_{ijq}-1)\cdot L_j-a_{ijq}\cdot L_q\\ & =N_{e,ijq}+\left[M_i+{\epsilon }_i+(a_{ijq}-1)\cdot (m_j+{\xi }_j)-a_{ijq}\cdot (m_q+{\xi }_q)\right]+{\beta }_i\end{array}$$

(3)

with

$$\{\begin{array}{l}{a}_{ijq}=({\lambda }_i^2+{\lambda }_j^2)/({\lambda }_j^2-{\lambda }_q^2)\hfill \\ N_{e,ijq}={\mu }_{r,i}+{\mu }_i+(a_{ijq}-1)\cdot (N_j+b_{r,j}+b_j)-a_{ijq}\cdot (N_q+b_{r,q}+b_q)\hfill \end{array}$$

(4)

where i, j and q denote three carrier frequencies, a denotes a linear factor, λ denotes the wavelength, N_e denotes the float phase ambiguity grouped with the constant code and phase hardware delays at both receiver and satellite ends, which is usually considered to be stable when there are no cycle slips, and the bracket describes the effects of multipath and noise errors in the MP combinations. For convenience, one of the carrier phase observations usually adopts the same frequency as the code observations in most practical applications, namely i = j or i = q. The means for selection of linear factor a is that the geometric contribution (antenna movement, satellite orbit, and satellite clock), tropospheric delay, and ionospheric delay cancel out. As shown in Equation (3), the MP combinations mainly contain the float phase ambiguity, the multipath and noise errors and the SICB. Therefore, the long-term changes—namely, the elevation-dependent SICB variations—can be detected by the MP combinations.

2.2. Traditional SICB Modeling

In traditional SICB modeling, the float phase ambiguities in Equation (3) are roughly determined as the average values of the MP combination time series over each continuous tracking arc [5,9]. After subtracting the estimated phase ambiguities from the MP combination time series, the remaining series are used to model the long-term changes, namely SICB, based on the relationship with elevation angles. When employing this method, only MP variations over continuous ambiguity blocks, rather than absolute MP values, can be acquired. Both the different tracking of a satellite at different stations and cycle slips can affect the absolute level of the remaining MP series. The consistency of different ambiguity blocks cannot be ensured. This is because the true integer phase ambiguities and hardware delay terms cannot be obtained. Additional biases will be brought in by the alignment of different MP combination time series with a removal of average values. The additional biases will degrade the modeling accuracy of SICB.

Figure 2 illustrates the MP combination time series of B1 signal with and without cycle slips at 500 consecutive epochs for BDS-2 MEO satellite C12 at station SGG1 on 13 July 2016. We artificially add a cycle slip at the 250th epoch so that its effects on SICB modeling can be analyzed. For the three continuous ambiguity arcs, the respective float phase ambiguities are calculated. It is clearly seen that there are constant differences between the absolute MP values with and without cycle slips. The MP differences reach −0.251 and 0.251 m before and after the cycle slip occurs, respectively. For further analysis, Figure 3 shows the MP combination time series as a function of elevations. The third-order polynomial fitting is conducted for the MP series, and these results are also provided in Figure 3. The MP fitting values with and without cycle slips show significant differences at elevation angles lower than 50° and higher than 70°, which will negatively affect the elevation-dependent modeling of SICB.

Figure 4 presents the MP combination time series of B1 signal at 800 consecutive epochs for BDS-2 MEO satellite C14 at stations ASCG (7.92°S, 14.33°W) and NKLG (0.35°N, 9.67°E) on 19 August 2016. The tracking time of C14 is different at the two stations located in different longitude and latitude regions. Figure 5 shows the dependence of the MP combination time series on the elevation angles. The third-order polynomial fitting is also carried out for these MP series. The MP fitting values at stations ASCG and NKLG show differences at both ends of elevations, but the MP differences with a level of several centimeters are much smaller than those caused by the cycle slips shown in Figure 3. The different tracking of a satellite at different stations also has navigate effects on the SICB modeling.

The results shown in Figure 2, Figure 3, Figure 4 and Figure 5 indicate that both the cycle slips and the different tracking of a satellite at different stations can negatively affect the SICB modeling due to the inconsistency of the absolute level of MP combinations caused by the calculation of float phase ambiguities, which is a severe flaw for the traditional SICB modeling approach. This flaw will degrade the modeling accuracy, and must be carefully repaired.

2.3. Improved SICB Modeling

Actually, we do not need to compute the float phase ambiguities. In this study, the between-elevation single-difference (BESD) is used to remove the invariable integer phase ambiguities and constant hardware delay terms so that the SICB modeling is free of the effects of MP combination inconsistency caused by the cycle slips and different tracking of a satellite at different stations. Elevation-dependent piecewise linear modeling is employed for SICB [5]. To describe more precise SICB variations, a denser elevation node separation of 1°, rather than the 5° or 10° adopted by previous studies, is used. The elevation node separation of 1° is empirically determined. If the separation is oversized, the accuracy of the developed model will degrade, because a lot of details about SICB variations are missing. If the separation is undersized, the errors caused by multipath effects and measurement noises will be enlarged, since the BESD processing is conducted. In view of the fact that the MP values at integer elevation angles cannot usually be obtained, the epochs with float elevation angles nearest to the respective integers are first singled out. The difference between the float elevation angle and its nearest integer should be smaller than 0.1° in this contribution. Assuming that the SICB linearly changes over elevation angles for a very small elevation range, the elevation-differenced (ED) SICB on the ith frequency for satellite s between two consecutive integer elevation angles E_k+1 and E_k at station r can be computed as:

$$\Delta {\beta }_i{(E_{k+1},E_k)}_r^s=\left[{\mathrm{MP}}_i{(t_{k+1},E_{f,k+1})}_r^s-{\mathrm{MP}}_i{(t_k,E_{f,k})}_r^s\right]/(E_{f,k+1}-E_{f,k})$$

(5)

where Δ stands for the BESD processing, and E_f,k and E_f,k+1 are the corresponding float elevation angles at epochs t_k and t_k+1, respectively. It is assumed that no cycle slips occur between epochs t_k and t_k+1.

Assuming there are a total of n sets of ED SICB estimates on the ith frequency for satellite s between integer elevation angles E_k+1 and E_k for all the selected stations and days, the average processing can be carried out to mitigate the effects of multipath errors and measurement noises, that is:

$$\Delta {\beta }_i{(E_{k+1},E_k)}^s=\left({\displaystyle \sum _{r=1}^n\Delta {\beta }_i{(E_{k+1},E_k)}_r^s}\right)/n$$

(6)

According to Equation (6), we can only obtain a series of precise ED SICB estimates. Assuming that the SICB at the elevation angle 45° (E_k0 = 45°) on the ith frequency for satellite s is d, the SICB estimates at an integer elevation angle E_k can be expressed as:

$$\{\begin{array}{ll}{\beta }_i{(E_k)}^s=d_i^s+{\displaystyle \sum _{p=k_0+1}^k\Delta {\beta }_i{(E_p,E_{p-1})}^s}\hfill & E_k>{45}^{\circ }\hfill \\ {\beta }_i{(E_k)}^s=d_i^s\hfill & E_k={45}^{\circ }\hfill \\ {\beta }_i{(E_k)}^s=d_i^s-{\displaystyle \sum _{p=k+1}^{k_0}\Delta {\beta }_i{(E_p,E_{p-1})}^s}\hfill & E_k<{45}^{\circ }\hfill \end{array}$$

(7)

For the purpose of fixing the absolute level of the SICB model, a zero-mean restriction is introduced for the model values of all used MP combinations [5]. Assuming that there is a total of n sets of MP combinations for all the selected stations and days on the ith frequency from satellite s, the following condition is introduced:

$${\displaystyle \sum _{p=1}^n{\beta }_i{(E_{k,p})}^s}=0$$

(8)

With Equation (8), the numerical value of the unknown parameter d can be solved. The absolute SICB model can be constructed with the solved parameter d. The reason for the selection of the reference elevation 45° is that the estimation accuracy of the ED SICBs at mid elevations is better than that at low and high elevations.

The SICB correction model and SICB model are opposite in sign. We establish the SICB correction model for each frequency and for each satellite using the observations from all the selected stations and days, as the SICB does not depend on the station location, receiver type or time.

3. Results and Discussion

The data sets from 60 globally distributed stations are adopted for analysis, as shown in Figure 6. The Multi-GNSS Experiment (MGEX) stations, which are marked in red and green, are all able to track signals on B1 and B2 frequencies for BDS-2 satellites. The green ones can also track the BDS-2 B3 signal. Both yellow and blue points refer to the international GNSS Monitoring and Assessment System (iGMAS) stations. The yellow ones have the capability of offering both B1/B2/B3 BDS-2 and B1/B3 BDS-3S tracking, while the blue ones are capable of tracking the B1, B2 and B3 signals of BDS-2 satellites. The station SGG1 located in Wuhan University and the iGMAS station XIA1, which are marked in black, can track all available signals for BDS-3S and BDS-2 satellites, except for B2 BDS-2 tracking at station XIA1. The analysis period spans a week from 7 to 13 July 2016 at station SGG1, two weeks from 2 to 15 September 2016 at station XIA1, and 32 days from 15 August to 15 September 2016 at other stations.

Figure 7 shows the time series of MP combinations of each BDS-2 and BDS-3S satellite at station SGG1 on 13 July 2016. We use the carrier phase observations on the B3 frequency to form the MP combinations for the code observations on the B1 and B1C frequencies, while the carrier phase observations on the B1 frequencies are used to form the B2, B3, B2a and B2b MP combinations. The MP combination time series of the B1C signal for C32 are not presented because of frequent gross errors. For the BDS-2 GEO satellites, the MP series contain apparent bias variations, which can reach up to 2 m on B1 and B2 frequencies, due to the severe ground multipath effects. Bias variations can also be observed in MP series from BDS-2 MEO and IGSO satellites, but with less fluctuation and smaller amplitude. With regard to BDS-3S satellites, no significant bias variations can be noticed, except for the C31. The MP series of C31 on the B1 frequency show systematic long-term variations, especially for the period 18:15~24:00 (Figure 7).

For further analysis, the root mean square (RMS) statistics of the high- and low-frequency components in the time series of MP combinations for each BDS-2 and BDS-3S satellite on each frequency are provided in Figure 8. We can separate the high- and low-frequency components in MP series using wavelet decomposition and reconstruction. We employ the Symlet wavelet “sym5”. The datasets from SGG1 on 7–13 July 2016 are adopted. The long-term changes, namely SICB variations, are mainly reflected by the low-frequency components, while the code multipath and noise (CMN) errors are mainly contained in the high-frequency components. The magnitude of phase multipath and noise (PMN) errors is very small, and thus they can be ignored. Actually, partial multipath effects will be also included in the low-frequency components, especially for the BDS-2 GEO satellites. Due to the presence of SICB, the RMSs of the low-frequency components are relatively larger for BDS-2 satellites, especially for the BDS-2 GEO satellites, the RMSs of which are enlarged by the severe ground multipath effects. For the new navigation signals and the legacy signal B3 of BDS-3S satellites, the RMSs of the low-frequency components are all smaller than 2.5 cm. Regarding the low-frequency components on B1 frequency for BDS-3S satellites, the corresponding RMS values are 7.2, 5.4, 3.1 and 4.1 cm for C31, C32, C33 and C34, respectively. We can conclude that the SICB variations should be very small for the BDS-3S satellites.

According to Zhou et al. [20], the results using a 40-m dish antenna to remove ground multipath effects revealed that the SICB variations still existed in the code observations of the three new navigation signals and two legacy signals of all four BDS-3S satellites, although they were confined to a peak amplitude of about 0.1 m. In addition, the elevation-dependent variations of SICB were still noticeable in the legacy bands of B1 and B3 for the BDS-3S IGSO satellites. As to the SICB values for the signals of BDS-3S MEO satellites on B1 and B3 frequencies and for all new navigation signals, they have a certain relationship with both azimuths and elevations. Thus, an effective elevation-dependent SICB correction model on the legacy B1 and B3 frequencies for BDS-3S IGSO satellites should be established. Moreover, we still establish the elevation-dependent SICB correction model for the signals of BDS-3S MEO satellites on B1 and B3 frequencies to further confirm the conclusions given in Zhou et al. [20].

The CMN can be used as an important index to characterize the quality of code observations. Figure 9 shows the dependence of RMSs of the high-frequency components in the time series of MP combinations on the satellite elevations at station SGG1. The RMSs are calculated for each increment of 5° in satellite elevations. It is clearly seen that B3, B2a and B2b exhibit the smallest CMN (Figure 9), which are signals with a high chipping rate of 10.23 Mcps. The chipping rates of all BDS signals are provided in Pan et al. [22]. The B2a, B2b and B3 signals of BDS-3S satellites show a comparable performance for CMN, and the RMS CMN is 15–23 cm at low elevation angles and 2–3 cm at zenith. As to the B1C signal of BDS-3S satellites, pseudorange errors of 13 cm are obtained close to zenith (90°), whereas increased values of about 0.6 m are encountered at low elevations. The RMS CMN of B1C signal is systematically larger than that of B1 signal by several centimeters because of the lower code chipping rate of B1C, which is equal to half that of B1 signal. The unexpected RMS statistics of CMN for B1 signal at satellite elevation angles from 30° to 50° can be attributed to the scarce observations. Compared with the BDS-3S satellites, the BDS-2 CMN on B1 and B3 frequencies show superior performance at mid and low elevations, and exceeds the BDS-3S CMN by several millimeters to 2 cm at elevation angles higher than 60°. The CMN for the BDS-2 B2 signal is of the same order of magnitude as that for the BDS-2 B1 signal. Differing surroundings near the station and the differing tracking performance of specific receivers and antennae in terms of multipath sensitivity will cause CMN differences, which can be revealed by direct comparison with the results from XIA1 of 2–15 September 2016 shown in the bottom sub-panels of Figure 9. The CMN results for B2a frequency at station XIA1 have to be excluded because of frequent gross errors.

Based on the MP combination time series from all the selected days and stations, the elevation-dependent piecewise linear correction model parameters for SICB with an elevation node separation of 1° are estimated for each frequency covered by this study, and for each BDS-3S and BDS-2 satellite. With the use of linear interpolation, we can obtain the SICB corrections between given nodes. We should add the corrections to the original code observations so that the SICB variations can be removed.

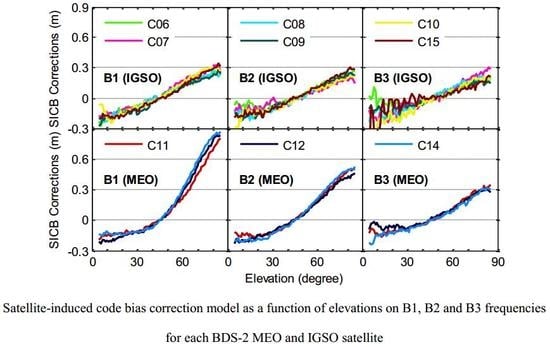
The estimated correction model parameters for BDS-2 satellites are shown in Figure 10. The code observations in the B1 band from BDS-2 MEO satellites are seriously impacted by SICB, and the SICB corrections reach approximately 0.9 m close to zenith. The SICB variations have much less effect on the BDS-2 IGSO satellites than the BDS-2 MEO satellites. The code observations on the B2 frequency are less affected by the SICB than those on the B1 frequency. The B3 signal has the smallest SICB corrections. The SICB corrections on the same frequency are very consistent for satellites with the same orbit type, and the differences among them are usually at a level of several centimeters. To pursue high accuracy, we still establish the SICB correction model for each satellite rather than IGSO-type or MEO-type satellites [10,11].

Figure 11 provides the estimated correction model parameters for BDS-3S satellites. In conjunction with the results shown in Figure 10, we can conclude that the SICB corrections for BDS-3S satellites are much smaller than those for BDS-2 satellites, and are usually confined to 0.1 m. It is interesting to notice that the SICB corrections on B3 frequency at elevations larger than 20° for C31 and at elevations larger than 40° for C32 are strongly elevation dependent, while the corresponding SICB corrections at other elevations are unstable due to the effects of the larger receiver CMN. We can deduce that the SICB corrections for the two legacy signals of all BDS-3S IGSO satellites depend on the elevations, although the elevation-dependent characteristics of SICB corrections with a small range of variance are severely contaminated by the receiver CMN for some cases. As to the BDS-3S MEO satellites, the estimated SICB corrections on the B1 frequency also seem to be elevation dependent. However, the SICB values of these satellites are different at the same elevation angles with different azimuth angles [20]. Thus, the established elevation-dependent SICB correction model for the B1 and B3 signals of BDS-3S MEO satellites is not applicable, as will be demonstrated in the following. The abnormal fluctuation of SICB corrections for the BDS-3S satellites at low elevations can be attributed to the larger CMN.

To validate the effectiveness of our SICB correction model, the SICB corrections are added to the original code observations to reform the MP combinations. Figure 12 illustrates the distribution of MP combination time series with application of SICB corrections for BDS-2 IGSO satellites. Datasets from 58 stations spanning 32 days are used. For the purpose of comparison, the distribution of original MP combination time series is also presented in this figure. It is clearly seen that both the uncorrected and corrected MP combinations are approximately normally distributed, but the expectations of the former ones show a slight deviation from zero. Compared with the original MP series, the MP series with SICB corrections account for larger percent of smaller errors. In each panel, the RMSs of MP series are also provided. The RMS values of corrected MP series are reduced by 7%, 6% and 2% over the uncorrected MP series on the B1, B2 and B3 frequencies, respectively. The corresponding results for BDS-2 MEO satellites are shown in Figure 13. The benefits from the SICB correction for IGSO satellites are smaller than those for MEO satellites. The decrease in RMS values for the corrected MP series over the uncorrected MP series is 18%, 14% and 5% on the three frequencies, respectively. Figure 12 involves 11.5, 11.5 and 5.4 million epoch-wise MP values for B1, B2 and B3 frequencies, respectively, while the corresponding numbers are 3.7, 3.7 and 2.1 million for the three frequencies in Figure 13, respectively. These numbers are just used to clarify the condition of the inputs for the SICB modeling. The number of epoch-wise MP values of BDS-2 MEO satellites is significantly smaller than that of BDS-2 IGSO satellites due to the relatively shorter tracking time. Theoretically, the accuracy of the model parameters will be improved when more datasets are involved in the SICB modeling. However, no more improvements can be achieved after the amount of data reaches a critical point, even if more datasets are subsequently included [23]. According to Li et al. [23], the number of epoch-wise MP values is sufficient for the SICB modeling in this study.

To further analyze the improved measurements, we reconstruct the elevation-dependent SICB correction model for the BDS-2 IGSO and MEO satellites using the code observations corrected by the previously established SICB correction model. The results are shown in Figure 14. It is clearly seen that the elevation-dependent model values after applying the SICB corrections are close to zero, indicating the successful correction of SICB for the code observations. The improved code measurements can be safely used for precise applications.

As shown in the Introduction section, many researchers have established various SICB correction models [5,8,9,10,11]. These existing models are all referred to as “traditional SICB correction models” in this paper. However, we cannot compare our improved SICB correction model with these traditional models one by one, because the datasets used for SICB modeling are different. For comparison, the traditional SICB correction model is also established by ourselves based on a comprehensive consideration of the advantages claimed for these traditional models [5,8,9,10,11]. The modeling strategies of the traditional SICB correction model can be summarized as: the lumped term of integer phase ambiguities and constant hardware delays is determined based on the average values of MP series obtained with original code observations over each continuous tracking arc; the elevation node separation is set to 5°; the model parameters are estimated by the least-squares adjustment for each satellite.

Table 1. Comparisons of the traditional and improved SICB correction models.

Item	Traditional SICB Correction Model	Improved SICB Correction Model	Superiority of Improved Model
Integer phase ambiguities and constant hardware delays	Estimated as average values of MP series over each continuous ambiguity block	Eliminated by between-elevation single difference	Free of effects of MP combination inconsistency
Elevation node separation	5°	1°	More precise elevation-dependent SICB variations
Estimation approach	Least-squares adjustment	Average processing	Easier implementation

summarizes the major characteristics of the traditional and improved SICB correction models to exhibit the differences between their modeling strategies.

The estimated model parameters of the traditional SICB correction model for BDS-2 IGSO and MEO satellites are provided in Figure 15. Compared with the modeling results shown in Figure 10, the traditional and improved SICB correction models have similar trends against elevations. However, the traditional SICB corrections miss a lot of detail about elevation-dependent variations, and fluctuate much more than the improved SICB corrections. In addition, the absolute level of SICB corrections also shows differences for the traditional and improved models. For example, the improved SICB corrections on the B3 frequency close to the zenith are approximately 0.3 m for C07, while the corresponding traditional SICB corrections are approximately 0.22 m.

After applying the SICB corrections derived from the traditional SICB correction model to the original code observations, the MP combinations are re-formed, and their distributions for the BDS-2 IGSO and MEO satellites are illustrated in Figure 16. The RMSs of the MP series are also computed and provided in each panel, and are 0.422, 0.364 and 0.400 m, and 0.448, 0.355 and 0.364 m for BDS-2 IGSO and MEO satellites on the B1, B2 and B3 frequencies, respectively. In conjunction with the results shown in Figure 12 and Figure 13, the above RMS statistics are smaller than those of uncorrected MP series, but slightly larger than those of corrected MP series with the improved SICB correction model proposed here, indicating that our improved SICB correction model outperforms the traditional SICB correction model.

Since the traditional SICB correction model cannot retrieve the effective elevation-dependent code biases for the BDS-3S satellites, the analysis of SICB mitigating for these satellites is confined to the improved SICB correction model. Figure 17 provides the distribution of MP combination time series without and with SICB corrections on B1 and B3 frequencies for BDS-3S IGSO satellites C31 and C32. Both uncorrected and corrected MP combinations are close to a normal distribution, but the latter ones account for a larger percent of smaller errors. The RMS statistics of the MP time series are calculated and displayed in each panel. About 0.32 and 0.35 million epoch-wise MP values are involved in the calculation of RMS values for C31 and C32, respectively. The decrease of the corrected MP series on the RMS values is 4% and 3% compared to the uncorrected MP series of the B1 and B3 frequencies for C31, respectively, while the corresponding decreases for C32 are 3% and 1% for the two frequencies, respectively. The reason for the small improvement is that the SICB variations on the two frequencies are at a level of only several centimeters for BDS-3S IGSO satellites. However, such a centimeter-level range of variance for SICB cannot be neglected for precise positioning applications in which code observations play a very important role. Benefiting from the consideration of MP combination consistency and the denser elevation node separation, the effective SICB correction model for the B1 and B3 signals of BDS-3S IGSO satellites is successfully established.

Figure 18 shows the distribution of uncorrected and corrected MP combination time series of B1 and B3 frequencies for BDS-3S MEO satellites C33 and C34. Both uncorrected and corrected MP combinations are approximately normally distributed. Moreover, the distribution is nearly identical for the two different groups of MP combinations. In each panel, the RMSs of MP series are also presented. Unlike the results shown in Figure 12, Figure 13 and Figure 17, the RMS values of MP time series of BDS-3S MEO satellites are slightly increased by 1–6 mm after applying the SICB corrections. This is because the SICB variations on B1 and B3 frequencies are related not only to the elevation angles, but also to the azimuth angles of BDS-3S MEO satellites [20]. Therefore, the elevation-dependent SICB correction model cannot be applied to these satellites. A further investigation of SICB modeling as a function of elevations and azimuths for these satellites is needed. In Figure 18, there are approximately 0.18 and 0.16 million epoch-wise MP values for C33 and C34, respectively.

For the single-frequency PPP technology, the GRoup And PHase Ionospheric Correction (GRAPHIC) [24], namely the ionospheric-free observable formed by the carrier phase and code observations on a single frequency, is usually used. Single-frequency PPP processing can be employed to further validate the effectiveness of our SICB correction model. Only BDS-2 IGSO and MEO satellites are adopted because the precise products are currently not available for the BDS-3S satellites. Another valid reason is that the SICB model works in the BDS-2 IGSO and MEO satellites, and the RMS MP combinations decrease compared with the uncorrected data, as shown in Figure 12 and Figure 13. The single-frequency PPP models developed by Cai et al. [25] are employed. The epoch-wise single-frequency PPP solutions without SICB corrections and with SICB corrections derived from the traditional and improved SICB correction models at station ANMG on 15 August 2016 are shown in Figure 19. When using the uncorrected observations, we find a significant systematic bias of approximately 0.8 m in the vertical direction. There are no such biases for the position solutions in the two horizontal directions. After considering the SICB corrections with the traditional or improved SICB correction models, the systematic biases almost completely vanish. The single-frequency PPP solutions using the improved SICB correction model show slightly better performance in terms of convergence time and positioning accuracy compared with those applying the traditional SICB correction model. The datasets from 21 stations for 15 August–15 September 2016 are used for the accuracy statistics. The BDS service of the Asia-Pacific area covers the selected stations. We calculate the RMSs of position errors over the last 15 min for each 24-h session. The average values of the RMSs over all the selected stations and days are listed in

Table 2. Average positioning accuracy of single-frequency PPP with and without SICB corrections for all 24-h sessions.

Direction	Uncorrected	Corrected (Improved SICB Model)	Corrected (Traditional SICB Model)
East (cm)	3.3	2.5	2.7
North (cm)	1.6	1.3	1.4
Up (cm)	79.4	9.1	9.7

. On the basis of average RMSs over all the sessions, the positioning accuracies of the single-frequency PPP using the uncorrected observations are 3.3, 1.6 and 79.4 cm in the east, north and vertical directions, respectively. Taking the SICB corrections into account with the improved SICB correction model, the positioning accuracies can be improved by 24%, 19% and 89% to 2.5, 1.3 and 9.1 cm in the three directions, respectively. When using the code observations with SICB corrections derived from the traditional SICB correction model, the positioning accuracies are 2.7, 1.4 and 9.7 cm in the three directions, respectively, which are significantly better than those ignoring SICB corrections, but slightly worse than those using our improved SICB correction model. The accuracy improvements for the single-frequency PPP applying the improved SICB correction model over the case using the traditional SICB correction model are 7%, 7% and 6% in the three directions, respectively.

4. Conclusions

An improved elevation-dependent SICB piecewise linear correction model with an elevation node separation of 1° in consideration of the consistency of the MP combinations is proposed in this study. We obtain effective SICB corrections for the code observations from BDS-2 IGSO and MEO satellites on B1, B2 and B3 frequencies, as well as the code observations from BDS-3S IGSO satellites on B1 and B3 frequencies. The correction parameters are estimated for each frequency and for each satellite. The traditional SICB correction model is also established for the purpose of comparison.

Significant differences can be observed for the elevation-dependent SICB corrections among the orbit types and frequency bands. The SICB variations have much more effect on the BDS-2 MEO satellites than the BDS-2 IGSO satellites. For BDS-2 satellites, the code observations on the B2 frequency are less affected by the SICB than those on the B1 frequency, while the B3 signal has the smallest SICB corrections. Elevation-dependent code biases are successfully removed after adding the SICB corrections to the code observations. After applying the improved SICB correction model, the RMS values of MP combination time series are reduced from 0.447, 0.381, and 0.406 m to 0.417, 0.360 and 0.398 m, and from 0.523, 0.405, and 0.382 m to 0.431, 0.348 and 0.363 m, on the B1, B2 and B3 frequencies for the BDS-2 IGSO and MEO satellites, respectively. With the traditional SICB correction model, the corresponding RMS MP combinations are 0.422, 0.364 and 0.400 m, and 0.448, 0.355 and 0.364 m on the three frequencies for the BDS-2 IGSO and MEO satellites, respectively, which are smaller than those of uncorrected MP series, but slightly larger than those of corrected MP series using the improved SICB correction model. Single-frequency PPP processing using BDS-2 IGSO and MEO satellites is carried out to validate the effectiveness and correctness of our improved model. The positioning accuracies of single-frequency PPP considering SICB corrections derived from the improved model are improved by 24%, 19% and 89%, and 7%, 7% and 6% compared with the case neglecting the SICB effects and the case using the SICB corrections computed by the traditional SICB correction model in east, north and vertical directions, respectively. Only centimeter-level SICB variations can be observed for all the signals of BDS-3S satellites. After applying the SICB corrections derived from the improved SICB correction model, the RMSs of MP series for B1 and B3 signals of BDS-3S IGSO satellites C31 and C32 are reduced from 0.505 and 0.433 m to 0.484 and 0.420 m, and from 0.499 and 0.397 m to 0.483 and 0.394 m, respectively.

Currently, the BDS-3 is under construction. As of 29 March 2018, there have been eight BDS-3 satellites. According to the performance of the code systematic biases for BDS-3S satellites, it is reasonable to infer that SICB variations at centimeter level will still exist in the code observations from BDS-3 satellites. Our approach can be well used to establish the SICB correction models for the BDS-3 satellites in the future.