Recalibration of over 35 Years of Infrared and Water Vapor Channel Radiances of the JMA Geostationary Satellites
Abstract
:1. Introduction
2. Data
2.1. Monitored Datasets: JMA Geostationary Satellites
2.2. Spectral Response Functions (SRFs) of Monitored and Reference Instrument
2.3. Reference Datasets
3. Methods
3.1. Principles of Common Recalibration Method
3.2. Application of Common Recalibration Method to JMA Satellites
3.2.1. Adjusting for Spectral Band Differences
3.2.2. GEO-LEO Collocations
Time Check
Satellite Zenith Angle Check
Environment Uniformity Check
Normality Check
Values of Each Threshold
3.3. Using Operational Radiance for Linear Fit Instead of Count
3.4. Route towards Applying Prime Reference Corrections
4. Results
4.1. Standard Radiance
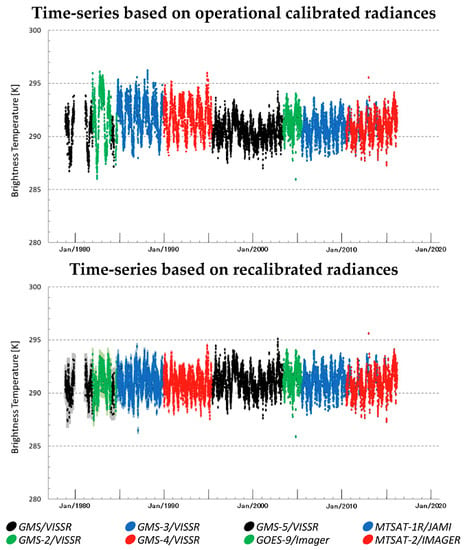
4.2. Evaluation of Time-Series of Recalibrated Data before Prime Reference Correction
4.3. Evaluation of Time-Series of Recalibrated Data after Prime Reference Correction
4.4. Applying Recalibration Coefficients to Actual Data
5. Discussion
5.1. SRF of GMS5/VISSR WV Channel
5.2. Variations in Diurnal Biases
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| AIRS | Atmospheric Infrared Sounder |
| CDR | Climate Data Records |
| DD | Double Difference |
| EUMETSAT | European Organization for the Exploitation of Meteorological Satellites |
| FCDR | Fundamental Climate Data Records |
| FoV | Field of View |
| GEO | Geostationary |
| GMS | Geostationary Metrological Satellite |
| GOES | Geostationary Operational Environmental Satellite |
| GSICS | Global Space-based Inter-calibration System |
| GVAR | GOES Variable Format |
| HIRS | High-Resolution Infrared Radiation Sounder |
| HRIT | High Rate Information Transmission |
| IASI | Infrared Atmospheric Sounding Interferometer |
| IFOV | Instantaneous field of view |
| IOGEO | Inter-calibration of imager observations from time-series of geostationary satellites |
| IR | Infrared |
| JAMI | Japanese Advanced Meteorological Imager |
| JMA | Japan Meteorological Agency |
| JRA-25 | Japanese 25-year Reanalysis |
| LEO | Low earth orbit |
| MDUS | Medium-scale Data Utilization Stations |
| MTSAT | Multi-functional Transport Satellite |
| NOAA | National Oceanic and Atmospheric Administration |
| SBAF | Spectral Band Adjustment Factor |
| SCOPE-CM | Sustained and Coordinated Processing of Environmental Satellite data for Climate Monitoring |
| SDUS | Small-scale Data Utilization Stations |
| SNO | Simultaneous Nadir Overpass |
| SRF | Spectral Response Function |
| SST | Sea Surface Temperature |
| SZA | Satellite zenith angle |
| VISSR | Visible and Infrared Spin Scan Radiometer |
| WMO | World Meteorological Organization |
| WV | Water Vapor |
Appendix A. Spectral Adjustment Factors (SBAFs) for Historical JMA’s Satellites and HIRS2
| Sensor to | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GMS/VISSR | GMS-2/VISSR | GMS-3/VISSR | GMS-4/VISSR | GMS-5/VISSR | GOES-9/Imager | MTSAT-1R/JAMI | MTSAT-2/IMAGER | |||
| Sensor from | TIROS-N/HIRS2 | offsetSBAF | 1.91388 × 100 | 1.76601 × 10−1 | 2.01927 × 100 | 3.41112 × 10−1 | −4.77384 × 10−1 | −7.68048 × 10−1 | −6.33724 × 10−1 | −6.92769 × 10−1 |
| slopeSBAF | 9.90390 × 10−1 | 9.66809 × 10−1 | 9.93578 × 10−1 | 9.55282 × 10−1 | 9.67450 × 10−1 | 9.57915 × 10−1 | 9.67629 × 10−1 | 9.68974 × 10−1 | ||
| var(offsetSBAF) | 1.69848 × 10−4 | 2.66605 × 10−4 | 2.39072 × 10−4 | 3.55870 × 10−4 | 4.51932 × 10−4 | 8.54050 × 10−4 | 5.15838 × 10−4 | 5.37767 × 10−4 | ||
| var(slopeSBAF) | 1.78400 × 10−8 | 2.80028 × 10−8 | 2.51108 × 10−8 | 3.73787 × 10−8 | 4.74685 × 10−8 | 8.97049 × 10−8 | 5.41809 × 10−8 | 5.64841 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −1.68816 × 10−6 | −2.64985 × 10−6 | −2.37619 × 10−6 | −3.53707 × 10−6 | −4.49185 × 10−6 | −8.48861 × 10−6 | −5.12704 × 10−6 | −5.34499 × 10−6 | ||
| NOAA06/HIRS2 | offsetSBAF | 2.02750 × 100 | 2.82410 × 10−1 | 2.13380 × 100 | 4.45310 × 10−1 | −3.72665 × 10−1 | −6.65897 × 10−1 | −5.29343 × 10−1 | −5.88399 × 10−1 | |
| slopeSBAF | 9.87999 × 10−1 | 9.64529 × 10−1 | 9.91174 × 10−1 | 9.53033 × 10−1 | 9.65181 × 10−1 | 9.55685 × 10−1 | 9.65363 × 10−1 | 9.66707 × 10−1 | ||
| var(offsetSBAF) | 2.29125 × 10−4 | 2.21170 × 10−4 | 3.10005 × 10−4 | 3.04405 × 10−4 | 3.82866 × 10−4 | 7.55096 × 10−4 | 4.39502 × 10−4 | 4.58042 × 10−4 | ||
| var(slopeSBAF) | 2.40049 × 10−8 | 2.31714 × 10−8 | 3.24785 × 10−8 | 3.18917 × 10−8 | 4.01118 × 10−8 | 7.91094 × 10−8 | 4.60455 × 10−8 | 4.79879 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.27427 × 10−6 | −2.19531 × 10−6 | −3.07708 × 10−6 | −3.02149 × 10−6 | −3.80028 × 10−6 | −7.49500 × 10−6 | −4.36245 × 10−6 | −4.54647 × 10−6 | ||
| NOAA07/HIRS2 | offsetSBAF | 1.87218 × 100 | 1.39050 × 10−1 | 1.97705 × 100 | 3.04381 × 10−1 | −5.14368 × 10−1 | −8.03609 × 10−1 | −6.70530 × 10−1 | −7.29586 × 10−1 | |
| slopeSBAF | 9.86798 × 10−1 | 9.63269 × 10−1 | 9.89978 × 10−1 | 9.51780 × 10−1 | 9.63902 × 10−1 | 9.54391 × 10−1 | 9.64078 × 10−1 | 9.65417 × 10−1 | ||
| var(offsetSBAF) | 1.52417 × 10−4 | 3.13191 × 10−4 | 2.13905 × 10−4 | 4.08756 × 10−4 | 5.10545 × 10−4 | 9.32785 × 10−4 | 5.78235 × 10−4 | 6.01147 × 10−4 | ||
| var(slopeSBAF) | 1.58798 × 10−8 | 3.26304 × 10−8 | 2.22860 × 10−8 | 4.25870 × 10−8 | 5.31920 × 10−8 | 9.71839 × 10−8 | 6.02444 × 10−8 | 6.26316 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −1.50882 × 10−6 | −3.10037 × 10−6 | −2.11750 × 10−6 | −4.04640 × 10−6 | −5.05403 × 10−6 | −9.23391 × 10−6 | −5.72412 × 10−6 | −5.95093 × 10−6 | ||
| NOAA08/HIRS2 | offsetSBAF | 1.97461 × 100 | 2.33758 × 10−1 | 2.08041 × 100 | 3.97508 × 10−1 | −4.20725 × 10−1 | −7.12543 × 10−1 | −5.77219 × 10−1 | −6.36274 × 10−1 | |
| slopeSBAF | 9.87304 × 10−1 | 9.63819 × 10−1 | 9.90480 × 10−1 | 9.52329 × 10−1 | 9.64464 × 10−1 | 9.54965 × 10−1 | 9.64644 × 10−1 | 9.65986 × 10−1 | ||
| var(offsetSBAF) | 1.99938 × 10−4 | 2.52768 × 10−4 | 2.73774 × 10−4 | 3.40659 × 10−4 | 4.27128 × 10−4 | 8.17494 × 10−4 | 4.87692 × 10−4 | 5.07741 × 10−4 | ||
| var(slopeSBAF) | 2.08953 × 10−8 | 2.64165 × 10−8 | 2.86118 × 10−8 | 3.56019 × 10−8 | 4.46386 × 10−8 | 8.54353 × 10−8 | 5.09680 × 10−8 | 5.30634 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −1.98218 × 10−6 | −2.50593 × 10−6 | −2.71419 × 10−6 | −3.37728 × 10−6 | −4.23452 × 10−6 | −8.10459 × 10−6 | −4.83495 × 10−6 | −5.03372 × 10−6 | ||
| NOAA09/HIRS2 | offsetSBAF | 1.91769 × 100 | 1.81067 × 10−1 | 2.02298 × 100 | 3.45683 × 10−1 | −4.72833 × 10−1 | −7.63243 × 10−1 | −6.29145 × 10−1 | −6.88200 × 10−1 | |
| slopeSBAF | 9.87255 × 10−1 | 9.63741 × 10−1 | 9.90435 × 10−1 | 9.52249 × 10−1 | 9.64379 × 10−1 | 9.54872 × 10−1 | 9.64557 × 10−1 | 9.65898 × 10−1 | ||
| var(offsetSBAF) | 1.72326 × 10−4 | 2.83934 × 10−4 | 2.39477 × 10−4 | 3.75907 × 10−4 | 4.70900 × 10−4 | 8.78543 × 10−4 | 5.35377 × 10−4 | 5.57029 × 10−4 | ||
| var(slopeSBAF) | 1.79872 × 10−8 | 2.96367 × 10−8 | 2.49963 × 10−8 | 3.92367 × 10−8 | 4.91520 × 10−8 | 9.17013 × 10−8 | 5.58820 × 10−8 | 5.81420 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −1.70743 × 10−6 | −2.81325 × 10−6 | −2.37277 × 10−6 | −3.72453 × 10−6 | −4.66574 × 10−6 | −8.70472 × 10−6 | −5.30459 × 10−6 | −5.51911 × 10−6 | ||
| NOAA10/HIRS2 | offsetSBAF | 1.94652 × 100 | 2.07778 × 10−1 | 2.05207 × 100 | 3.71955 × 10−1 | −4.46412 × 10−1 | −7.37530 × 10−1 | −6.02814 × 10−1 | −6.61868 × 10−1 | |
| slopeSBAF | 9.87366 × 10−1 | 9.63865 × 10−1 | 9.90544 × 10−1 | 9.52372 × 10−1 | 9.64506 × 10−1 | 9.55002 × 10−1 | 9.64685 × 10−1 | 9.66026 × 10−1 | ||
| var(offsetSBAF) | 1.85616 × 10−4 | 2.67878 × 10−4 | 2.56116 × 10−4 | 3.57780 × 10−4 | 4.48570 × 10−4 | 8.47561 × 10−4 | 5.11096 × 10−4 | 5.31964 × 10−4 | ||
| var(slopeSBAF) | 1.93900 × 10−8 | 2.79833 × 10−8 | 2.67546 × 10−8 | 3.73747 × 10−8 | 4.68588 × 10−8 | 8.85386 × 10−8 | 5.33905 × 10−8 | 5.55705 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −1.83982 × 10−6 | −2.65519 × 10−6 | −2.53861 × 10−6 | −3.54629 × 10−6 | −4.44619 × 10−6 | −8.40097 × 10−6 | −5.06596 × 10−6 | −5.27280 × 10−6 | ||
| NOAA11/HIRS2 | offsetSBAF | 2.03568 × 100 | 2.89736 × 10−1 | 2.14209 × 100 | 4.52470 × 10−1 | −3.65458 × 10−1 | −6.58983 × 10−1 | −5.22169 × 10−1 | −5.81224 × 10−1 | |
| slopeSBAF | 9.88776 × 10−1 | 9.65294 × 10−1 | 9.91952 × 10−1 | 9.53790 × 10−1 | 9.65948 × 10−1 | 9.56447 × 10−1 | 9.66131 × 10−1 | 9.67475 × 10−1 | ||
| var(offsetSBAF) | 2.33900 × 10−4 | 2.12582 × 10−4 | 3.16437 × 10−4 | 2.94454 × 10−4 | 3.71777 × 10−4 | 7.39774 × 10−4 | 4.27684 × 10−4 | 4.46036 × 10−4 | ||
| var(slopeSBAF) | 2.45477 × 10−8 | 2.23104 × 10−8 | 3.32099 × 10−8 | 3.09028 × 10−8 | 3.90178 × 10−8 | 7.76388 × 10−8 | 4.48852 × 10−8 | 4.68112 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.32367 × 10−6 | −2.11189 × 10−6 | −3.14363 × 10−6 | −2.92524 × 10−6 | −3.69340 × 10−6 | −7.34925 × 10−6 | −4.24881 × 10−6 | −4.43112 × 10−6 | ||
| NOAA12/HIRS2 | offsetSBAF | 1.95577 × 100 | 2.16297 × 10−1 | 2.06140 × 100 | 3.80329 × 10−1 | −4.37996 × 10−1 | −7.29355 × 10−1 | −5.94429 × 10−1 | −6.53484 × 10−1 | |
| slopeSBAF | 9.87367 × 10−1 | 9.63871 × 10−1 | 9.90545 × 10−1 | 9.52379 × 10−1 | 9.64514 × 10−1 | 9.55011 × 10−1 | 9.64693 × 10−1 | 9.66034 × 10−1 | ||
| var(offsetSBAF) | 1.90436 × 10−4 | 2.62360 × 10−4 | 2.62127 × 10−4 | 3.51532 × 10−4 | 4.40846 × 10−4 | 8.36786 × 10−4 | 5.02700 × 10−4 | 5.23283 × 10−4 | ||
| var(slopeSBAF) | 1.98972 × 10−8 | 2.74120 × 10−8 | 2.73877 × 10−8 | 3.67290 × 10−8 | 4.60607 × 10−8 | 8.74295 × 10−8 | 5.25234 × 10−8 | 5.46739 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −1.88776 × 10−6 | −2.60072 × 10−6 | −2.59842 × 10−6 | −3.48467 × 10−6 | −4.37003 × 10−6 | −8.29491 × 10−6 | −4.98318 × 10−6 | −5.18721 × 10−6 | ||
| NOAA14/HIRS2 | offsetSBAF | 1.94430 × 100 | 2.05639 × 10−1 | 2.04984 × 100 | 3.69835 × 10−1 | −4.48538 × 10−1 | −7.39631 × 10−1 | −6.04935 × 10−1 | −6.63989 × 10−1 | |
| slopeSBAF | 9.87541 × 10−1 | 9.64035 × 10−1 | 9.90719 × 10−1 | 9.52540 × 10−1 | 9.64676 × 10−1 | 9.55170 × 10−1 | 9.64855 × 10−1 | 9.66197 × 10−1 | ||
| var(offsetSBAF) | 1.84538 × 10−4 | 2.67504 × 10−4 | 2.55042 × 10−4 | 3.57283 × 10−4 | 4.48473 × 10−4 | 8.47573 × 10−4 | 5.11111 × 10−4 | 5.32036 × 10−4 | ||
| var(slopeSBAF) | 1.92833 × 10−8 | 2.79528 × 10−8 | 2.66507 × 10−8 | 3.73343 × 10−8 | 4.68632 × 10−8 | 8.85673 × 10−8 | 5.34086 × 10−8 | 5.55951 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −1.82941 × 10−6 | −2.65189 × 10−6 | −2.52836 × 10−6 | −3.54192 × 10−6 | −4.44593 × 10−6 | −8.40241 × 10−6 | −5.06689 × 10−6 | −5.27433 × 10−6 | ||
| Sensor to | ||||||
|---|---|---|---|---|---|---|
| GMS-5/VISSR | GOES-9/Imager | MTSAT-1R/JAMI | MTSAT-2/IMAGER | |||
| Sensor from | TIROS-N/HIRS2 | offsetSBAF | −1.85938 × 10−1 | 1.97179 × 10−2 | 1.62528 × 10−2 | −3.78720 × 10−2 |
| slopeSBAF | 1.47261 × 100 | 1.01202 × 100 | 1.00164 × 100 | 1.06814 × 100 | ||
| var(offsetSBAF) | 1.61247 × 10−4 | 5.55424 × 10−7 | 9.81323 × 10−8 | 2.31180 × 10−6 | ||
| var(slopeSBAF) | 4.42476 × 10−6 | 1.52413 × 10−8 | 2.69283 × 10−9 | 6.34377 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.59555 × 10−5 | −8.94052 × 10−8 | −1.57961 × 10−8 | −3.72124 × 10−7 | ||
| NOAA06/HIRS2 | offsetSBAF | −1.79486 × 10−1 | 3.45212 × 10−2 | 3.14738 × 10−2 | −2.32147 × 10−2 | |
| slopeSBAF | 1.43619 × 100 | 9.85265 × 10−1 | 9.75072 × 10−1 | 1.04007 × 100 | ||
| var(offsetSBAF) | 1.31121 × 10−4 | 5.20833 × 10−8 | 3.32831 × 10−7 | 4.29153 × 10−7 | ||
| var(slopeSBAF) | 3.42645 × 10−6 | 1.36104 × 10−9 | 8.69753 × 10−9 | 1.12146 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.05938 × 10−5 | −8.18016 × 10−9 | −5.22742 × 10−8 | −6.74024 × 10−8 | ||
| NOAA07/HIRS2 | offsetSBAF | −1.95631 × 10−1 | 1.11726 × 10−2 | 7.69606 × 10−3 | −4.66388 × 10−2 | |
| slopeSBAF | 1.49000 × 100 | 1.02430 × 100 | 1.01381 × 100 | 1.08106 × 100 | ||
| var(offsetSBAF) | 1.67300 × 10−4 | 7.71710 × 10−7 | 1.82324 × 10−7 | 2.90173 × 10−6 | ||
| var(slopeSBAF) | 4.69017 × 10−6 | 2.16345 × 10−8 | 5.11136 × 10−9 | 8.13486 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.72218 × 10−5 | −1.25567 × 10−7 | −2.96664 × 10−8 | −4.72149 × 10−7 | ||
| NOAA08/HIRS2 | offsetSBAF | −1.83629 × 10−1 | 2.35588 × 10−2 | 2.01779 × 10−2 | −3.39961 × 10−2 | |
| slopeSBAF | 1.46758 × 100 | 1.00818 × 100 | 9.97822 × 10−1 | 1.06412 × 100 | ||
| var(offsetSBAF) | 1.54375 × 10−4 | 3.14121 × 10−7 | 2.01207 × 10−8 | 1.79865 × 10−6 | ||
| var(slopeSBAF) | 4.20920 × 10−6 | 8.56486 × 10−9 | 5.48615 × 10−10 | 4.90421 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.47691 × 10−5 | −5.04001 × 10−8 | −3.22834 × 10−9 | −2.88590 × 10−7 | ||
| NOAA09/HIRS2 | offsetSBAF | −2.02944 × 10−1 | 1.15862 × 10−2 | 8.40899 × 10−3 | −4.66915 × 10−2 | |
| slopeSBAF | 1.47493 × 100 | 1.01301 × 100 | 1.00259 × 100 | 1.06923 × 100 | ||
| var(offsetSBAF) | 1.51153 × 10−4 | 1.92885 × 10−7 | 3.47610 × 10−9 | 1.58942 × 10−6 | ||
| var(slopeSBAF) | 4.14514 × 10−6 | 5.28958 × 10−9 | 9.53267 × 10−11 | 4.35874 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.43248 × 10−5 | −3.10407 × 10−8 | −5.59403 × 10−10 | −2.55783 × 10−7 | ||
| NOAA10/HIRS2 | offsetSBAF | −1.82509 × 10−1 | 2.41579 × 10−2 | 2.07615 × 10−2 | −3.33496 × 10−2 | |
| slopeSBAF | 1.46885 × 100 | 1.00908 × 100 | 9.98713 × 10−1 | 1.06507 × 100 | ||
| var(offsetSBAF) | 1.54845 × 10−4 | 3.29542 × 10−7 | 2.33612 × 10−8 | 1.83479 × 10−6 | ||
| var(slopeSBAF) | 4.23036 × 10−6 | 9.00309 × 10−9 | 6.38228 × 10−10 | 5.01265 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.48689 × 10−5 | −5.29263 × 10−8 | −3.75194 × 10−9 | −2.94678 × 10−7 | ||
| NOAA11/HIRS2 | offsetSBAF | −1.79038 × 10−1 | 2.60182 × 10−2 | 2.25676 × 10−2 | −3.14329 × 10−2 | |
| slopeSBAF | 1.44894 × 100 | 9.95486 × 10−1 | 9.85269 × 10−1 | 1.05073 × 100 | ||
| var(offsetSBAF) | 1.56431 × 10−4 | 4.44147 × 10−7 | 9.09365 × 10−8 | 1.89794 × 10−6 | ||
| var(slopeSBAF) | 4.16184 × 10−6 | 1.18165 × 10−8 | 2.41936 × 10−9 | 5.04946 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.47924 × 10−5 | −7.03916 × 10−8 | −1.44123 × 10−8 | −3.00800 × 10−7 | ||
| NOAA12/HIRS2 | offsetSBAF | −1.56940 × 10−1 | 5.16489 × 10−2 | 4.85065 × 10−2 | −5.33506 × 10−3 | |
| slopeSBAF | 1.41891 × 100 | 9.73136 × 10−1 | 9.63054 × 10−1 | 1.02730 × 100 | ||
| var(offsetSBAF) | 1.26062 × 10−4 | 1.38418 × 10−7 | 5.20223 × 10−7 | 2.51211 × 10−7 | ||
| var(slopeSBAF) | 3.23127 × 10−6 | 3.54796 × 10−9 | 1.33345 × 10−8 | 6.43910 × 10−9 | ||
| cov(offsetSBAF,slopeSBAF) | −1.96059 × 10−5 | −2.15274 × 10−8 | −8.09078 × 10−8 | −3.90696 × 10−8 | ||
| NOAA14/HIRS2 | offsetSBAF | −1.75782 × 10−1 | 2.48681 × 10−2 | 2.12420 × 10−2 | −3.23335 × 10−2 | |
| slopeSBAF | 1.46146 × 100 | 1.00466 × 100 | 9.94383 × 10−1 | 1.06036 × 100 | ||
| var(offsetSBAF) | 1.66607 × 10−4 | 8.48391 × 10−7 | 2.47918 × 10−7 | 2.77531 × 10−6 | ||
| var(slopeSBAF) | 4.51304 × 10−6 | 2.29811 × 10−8 | 6.71557 × 10−9 | 7.51772 × 10−8 | ||
| cov(offsetSBAF,slopeSBAF) | −2.66441 × 10−5 | −1.35676 × 10−7 | −3.96474 × 10−8 | −4.43832 × 10−7 | ||
| Sensor to | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| GMS/VISSR | GMS−2/VISSR | GMS−3/VISSR | GMS−4/VISSR | GMS−5/VISSR | GOES−9/Imager | MTSAT−1R/JAMI | MTSAT−2/IMAGER | |||
| Sensor from | GMS/VISSR | offsetSBAF | −1.66220 × 100 | 9.63162 × 10−2 | −1.47425 × 100 | −2.31028 × 100 | −2.46489 × 100 | −2.52568 × 100 | −2.57439 × 100 | |
| slopeSBAF | 9.75882 × 10−1 | 1.00325 × 100 | 9.64230 × 10−1 | 9.76454 × 10−1 | 9.76613 × 10−1 | 9.77962 × 10−1 | 9.66742 × 10−1 | |||
| var(offsetSBAF) | 7.08338 × 10−4 | 1.01058 × 10−5 | 8.21350 × 10−4 | 1.04627 × 10−3 | 1.15493 × 10−3 | 1.19574 × 10−3 | 1.62344 × 10−3 | |||
| var(slopeSBAF) | 7.30167 × 10−8 | 1.04172 × 10−9 | 8.46661 × 10−8 | 1.07851 × 10−7 | 1.19052 × 10−7 | 1.23258 × 10−7 | 1.67347 × 10−7 | |||
| cov(offsetSBAF,slopeSBAF) | −6.98278 × 10−6 | −9.96223 × 10−8 | −8.09684 × 10−6 | −1.03140 × 10−5 | −1.13853 × 10−5 | −1.17875 × 10−5 | −1.60038 × 10−5 | |||
| GMS−2/VISSR | offsetSBAF | 1.77343 × 100 | 1.88287 × 100 | 1.62233 × 10−1 | −6.61716 × 10−1 | −9.63550 × 10−1 | −8.20166 × 10−1 | −8.80016 × 10−1 | ||
| slopeSBAF | 1.02395 × 100 | 1.02720 × 100 | 9.88125 × 10−1 | 1.00075 × 100 | 9.91025 × 10−1 | 1.00095 × 100 | 1.00235 × 100 | |||
| var(offsetSBAF) | 7.17986 × 10−4 | 8.83589 × 10−4 | 9.28503 × 10−6 | 3.32474 × 10−5 | 1.87663 × 10−4 | 5.56705 × 10−5 | 6.54543 × 10−5 | |||
| var(slopeSBAF) | 8.03867 × 10−8 | 9.89278 × 10−8 | 1.03956 × 10−9 | 3.72242 × 10−9 | 2.10110 × 10−8 | 6.23294 × 10−9 | 7.32835 × 10−9 | |||
| cov(offsetSBAF,slopeSBAF) | −7.36856 × 10−6 | −9.06812 × 10−6 | −9.52905 × 10−8 | −3.41212 × 10−7 | −1.92596 × 10−6 | −5.71336 × 10−7 | −6.71746 × 10−7 | |||
| GMS−3/VISSR | offsetSBAF | −9.50385 × 10−2 | −1.74765 × 100 | −1.55785 × 100 | −2.39430 × 100 | −2.65522 × 100 | −2.54847 × 100 | −2.60922 × 100 | ||
| slopeSBAF | 9.96751 × 10−1 | 9.72635 × 10−1 | 9.61014 × 10−1 | 9.73190 × 10−1 | 9.63486 × 10−1 | 9.73344 × 10−1 | 9.74687 × 10−1 | |||
| var(offsetSBAF) | 1.00592 × 10−5 | 8.67701 × 10−4 | 9.93763 × 10−4 | 1.23638 × 10−3 | 1.85833 × 10−3 | 1.35457 × 10−3 | 1.39921 × 10−3 | |||
| var(slopeSBAF) | 1.02827 × 10−9 | 8.86975 × 10−8 | 1.01584 × 10−7 | 1.26385 × 10−7 | 1.89961 × 10−7 | 1.38466 × 10−7 | 1.43029 × 10−7 | |||
| cov(offsetSBAF,slopeSBAF) | −9.87545 × 10−8 | −8.51849 × 10−6 | −9.75607 × 10−6 | −1.21379 × 10−5 | −1.82438 × 10−5 | −1.32982 × 10−5 | −1.37365 × 10−5 | |||
| GMS−4/VISSR | offsetSBAF | 1.61239 × 100 | −1.63229 × 10−1 | 1.72216 × 100 | −8.26073 × 10−1 | −1.12834 × 100 | −9.84821 × 10−1 | −1.04497 × 100 | ||
| slopeSBAF | 1.03618 × 100 | 1.01201 × 100 | 1.03945 × 100 | 1.01277 × 100 | 1.00296 × 100 | 1.01299 × 100 | 1.01440 × 100 | |||
| var(offsetSBAF) | 8.55527 × 10−4 | 9.54143 × 10−6 | 1.03990 × 10−3 | 2.27494 × 10−5 | 1.37519 × 10−4 | 3.99740 × 10−5 | 4.83457 × 10−5 | |||
| var(slopeSBAF) | 9.77723 × 10−8 | 1.09042 × 10−9 | 1.18843 × 10−7 | 2.59988 × 10−9 | 1.57161 × 10−8 | 4.56835 × 10−9 | 5.52509 × 10−9 | |||
| cov(offsetSBAF,slopeSBAF) | −8.87162 × 10−6 | −9.89425 × 10−8 | −1.07836 × 10−5 | −2.35907 × 10−7 | −1.42604 × 10−6 | −4.14522 × 10−7 | −5.01334 × 10−7 | |||
| GMS−5/VISSR | offsetSBAF | 2.46871 × 100 | 6.64519 × 10−1 | 2.58182 × 100 | 8.17876 × 10−1 | −3.12631 × 10−1 | −1.59229 × 10−1 | −2.18470 × 10−1 | ||
| slopeSBAF | 1.02299 × 100 | 9.99218 × 10−1 | 1.02621 × 100 | 9.87363 × 10−1 | 9.90334 × 10−1 | 1.00022 × 100 | 1.00162 × 100 | |||
| var(offsetSBAF) | 1.04454 × 10−3 | 3.27466 × 10−5 | 1.24006 × 10−3 | 2.18046 × 10−5 | 6.69374 × 10−5 | 3.90236 × 10−6 | 7.15730 × 10−6 | |||
| var(slopeSBAF) | 1.18374 × 10−7 | 3.71107 × 10−9 | 1.40532 × 10−7 | 2.47105 × 10−9 | 7.58580 × 10−9 | 4.42242 × 10−10 | 8.11113 × 10−10 | |||
| cov(offsetSBAF,slopeSBAF) | −1.07804 × 10−5 | −3.37969 × 10−7 | −1.27983 × 10−5 | −2.25040 × 10−7 | −6.90844 × 10−7 | −4.02752 × 10−8 | −7.38686 × 10−8 | |||
| GOES−9/Imager | offsetSBAF | 2.82493 × 100 | 9.91183 × 10−1 | 2.94154 × 100 | 1.13866 × 100 | 3.22524 × 10−1 | 1.62101 × 10−1 | 1.02914 × 10−1 | ||
| slopeSBAF | 1.03260 × 100 | 1.00885 × 100 | 1.03583 × 100 | 9.96899 × 10−1 | 1.00968 × 100 | 1.00992 × 100 | 1.01134 × 100 | |||
| var(offsetSBAF) | 1.64157 × 10−3 | 1.87209 × 10−4 | 1.88778 × 10−3 | 1.33499 × 10−4 | 6.77966 × 10−5 | 4.66295 × 10−5 | 4.21352 × 10−5 | |||
| var(slopeSBAF) | 1.90924 × 10−7 | 2.17735 × 10−8 | 2.19560 × 10−7 | 1.55267 × 10−8 | 7.88514 × 10−9 | 5.42328 × 10−9 | 4.90057 × 10−9 | |||
| cov(offsetSBAF,slopeSBAF) | −1.71598 × 10−5 | −1.95695 × 10−6 | −1.97335 × 10−5 | −1.39551 × 10−6 | −7.08698 × 10−7 | −4.87432 × 10−7 | −4.40452 × 10−7 | |||
| MTSAT−1R/JAMI | offsetSBAF | 2.63706 × 100 | 8.24893 × 10−1 | 2.75116 × 100 | 9.76090 × 10−1 | 1.59586 × 10−1 | −1.55842 × 10−1 | −5.91505 × 10−2 | ||
| slopeSBAF | 1.02270 × 100 | 9.98986 × 10−1 | 1.02592 × 100 | 9.87137 × 10−1 | 9.99778 × 10−1 | 9.90128 × 10−1 | 1.00140 × 100 | |||
| var(offsetSBAF) | 1.14873 × 10−3 | 5.46277 × 10−5 | 1.35354 × 10−3 | 3.81712 × 10−5 | 3.88782 × 10−6 | 4.58671 × 10−5 | 6.09307 × 10−7 | |||
| var(slopeSBAF) | 1.30554 × 10−7 | 6.20846 × 10−9 | 1.53830 × 10−7 | 4.33817 × 10−9 | 4.41853 × 10−10 | 5.21282 × 10−9 | 6.92481 × 10−11 | |||
| cov(offsetSBAF,slopeSBAF) | −1.18715 × 10−5 | −5.64543 × 10−7 | −1.39880 × 10−5 | −3.94475 × 10−7 | −4.01782 × 10−8 | −4.74008 × 10−7 | −6.29681 × 10−9 | |||
| MTSAT−2/IMAGER | offsetSBAF | 2.69933 × 100 | 8.84406 × 10−1 | 2.81379 × 100 | 1.03483 × 100 | 2.18833 × 10−1 | −9.75581 × 10−2 | 5.91289 × 10−2 | ||
| slopeSBAF | 1.02125 × 100 | 9.97584 × 10−1 | 1.02447 × 100 | 9.85752 × 10−1 | 9.98378 × 10−1 | 9.88745 × 10−1 | 9.98601 × 10−1 | |||
| var(offsetSBAF) | 1.18455 × 10−3 | 6.39705 × 10−5 | 1.39253 × 10−3 | 4.59800 × 10−5 | 7.10202 × 10−6 | 4.12799 × 10−5 | 6.06862 × 10−7 | |||
| var(slopeSBAF) | 1.34412 × 10−7 | 7.25881 × 10−9 | 1.58013 × 10−7 | 5.21741 × 10−9 | 8.05876 × 10−10 | 4.68409 × 10−9 | 6.88614 × 10−11 | |||
| cov(offsetSBAF,slopeSBAF) | −1.22314 × 10−5 | −6.60548 × 10−7 | −1.43791 × 10−5 | −4.74781 × 10−7 | −7.33342 × 10−8 | −4.26249 × 10−7 | −6.26635 × 10−9 | |||
| Sensor to | ||||||
|---|---|---|---|---|---|---|
| GMS−5/VISSR | GOES−9/Imager | MTSAT−1R/JAMI | MTSAT−2/IMAGER | |||
| Sensor from | GMS−5/VISSR | offsetSBAF | 2.51467 × 10−1 | 2.51298 × 10−1 | 1.97006 × 10−1 | |
| slopeSBAF | 6.74926 × 10−1 | 6.67337 × 10−1 | 7.13507 × 10−1 | |||
| var(offsetSBAF) | 5.93108 × 10−5 | 6.46618 × 10−5 | 5.48872 × 10−5 | |||
| var(slopeSBAF) | 7.81048 × 10−7 | 8.51513 × 10−7 | 7.22795 × 10−7 | |||
| cov(offsetSBAF,slopeSBAF) | −6.60171 × 10−6 | −7.19731 × 10−6 | −6.10933 × 10−6 | |||
| GOES−9/Imager | offsetSBAF | −2.27524 × 10−1 | −2.75796 × 10−3 | −5.94034 × 10−2 | ||
| slopeSBAF | 1.45729 × 100 | 9.89665 × 10−1 | 1.05558 × 100 | |||
| var(offsetSBAF) | 1.36760 × 10−4 | 1.98141 × 10−7 | 7.20279 × 10−7 | |||
| var(slopeSBAF) | 3.64130 × 10−6 | 5.27559 × 10−9 | 1.91778 × 10−8 | |||
| cov(offsetSBAF,slopeSBAF) | −2.16883 × 10−5 | −3.14224 × 10−8 | −1.14227 × 10−7 | |||
| MTSAT−1R//JAMI | offsetSBAF | −2.15036 × 10−1 | 3.09930 × 10−3 | −5.56419 × 10−2 | ||
| slopeSBAF | 1.47108 × 100 | 1.01039 × 100 | 1.06646 × 100 | |||
| var(offsetSBAF) | 1.52078 × 10−4 | 2.02101 × 10−7 | 1.61356 × 10−6 | |||
| var(slopeSBAF) | 4.13782 × 10−6 | 5.49885 × 10−9 | 4.39024 × 10−8 | |||
| cov(offsetSBAF,slopeSBAF) | −2.43795 × 10−5 | −3.23986 × 10−8 | −2.58668 × 10−7 | |||
| MTSAT−2/IMAGER | offsetSBAF | −1.56969 × 10−1 | 5.72652 × 10−2 | 5.43706 × 10−2 | ||
| slopeSBAF | 1.38240 × 100 | 9.47188 × 10−1 | 9.37326 × 10−1 | |||
| var(offsetSBAF) | 1.11529 × 10−4 | 6.34735 × 10−7 | 1.39406 × 10−6 | |||
| var(slopeSBAF) | 2.71321 × 10−6 | 1.54415 × 10−8 | 3.39138 × 10−8 | |||
| cov(offsetSBAF,slopeSBAF) | −1.68974 × 10−5 | −9.61669 × 10−8 | −2.11210 × 10−7 | |||
Appendix B. Sensor Planck Functions for IR and WV Channels on Old JMA Satellites
| Brightness temperature to radiance | Radiance to brightness temperature |
| where | where |
| Satellite/Sensor | Channel | Band Correction Coefficient | ||||
|---|---|---|---|---|---|---|
| a1 | a2 | b0 | b1 | b2 | ||
| c0 | c1 | c2 | ||||
| GMS/ VISSR | IR | 8255.3989526 | 1273.2972334 | 2.2757022 | 0.9884318 | 1.1793267 × 10−5 |
| −2.2992685 | 1.0117148 | −1.2013300 × 10−5 | ||||
| GMS–2/ VISSR | IR | 9214.2439210 | 1320.7998423 | 1.7428946 | 0.9911486 | 9.4229928 × 10−6 |
| −1.7565093 | 1.0089361 | −9.5518013 × 10−6 | ||||
| GMS–3/ VISSR | IR | 8186.0813819 | 1269.7234079 | 2.2231054 | 0.9890761 | 1.0258679 × 10−5 |
| −2.2453430 | 1.0110581 | −1.0452023 × 10−5 | ||||
| GMS–4/ VISSR | IR | 9317.0102296 | 1325.6919859 | 2.2092520 | 0.9890098 | 1.1306309 × 10−5 |
| −2.2309816 | 1.0111233 | −1.1504885 × 10−5 | ||||
| GMS–5/ VISSR | IR | 9436.1509182 | 1331.3188041 | 0.7365781 | 0.9965505 | 3.0927987 × 10−6 |
| −0.7389203 | 1.0034631 | −3.1116802 × 10−6 | ||||
| WV | 35,926.6023447 | 2078.8468183 | 0.5568513 | 0.9984068 | 7.5627042 × 10−7 | |
| −0.5577277 | 1.0015964 | −7.5910270 × 10−7 | ||||
| GOES–9/ Imager | IR | 9718.2592835 | 1344.4560220 | 0.5130980 | 0.9976226 | 2.1068265 × 10−6 |
| −0.5142247 | 1.0023838 | −2.1157521 × 10−6 | ||||
| WV | 38,729.0279165 | 2131.5521983 | 0.5228348 | 0.9985389 | 6.7751021 × 10−7 | |
| −0.5235900 | 1.0014638 | −6.7985173 × 10−7 | ||||
| MTSAT–1R/ JAMI | IR | 9475.9080697 | 1333.1859242 | 0.4912293 | 0.9976921 | 2.0915292 × 10−6 |
| −0.4922710 | 1.0023139 | −2.0999958 × 10−6 | ||||
| WV | 38,784.1056187 | 2132.5621676 | 0.4165452 | 0.9988113 | 6.0328185 × 10−7 | |
| −0.4170332 | 1.0011905 | −6.0493393 × 10−7 | ||||
| MTSAT–2/ IMAGER | IR | 9471.3339906 | 1332.9715704 | 0.4036895 | 0.9981173 | 1.6749284 × 10−6 |
| −0.4043903 | 1.0018867 | −1.6805293 × 10−6 | ||||
| WV | 38,352.6325483 | 2124.6247169 | 0.4006764 | 0.9988567 | 5.7395127 × 10−7 | |
| −0.4011279 | 1.0011449 | −5.7546785 × 10−7 | ||||
Appendix C. Prime Reference Correction Parameters
| LEO Instrument | SRF of GEO | offsetprime | slopeprime | var (offsetprime) | var (slopeprime) | cov(offsetprime,slopeprime) | corr. vol. at Standard Radiance [K] | corr. uncert. at Standard Radiance [K] |
|---|---|---|---|---|---|---|---|---|
| Metop−B/IASI | MTSAT−2/IMAGER | 0.080570 | 0.999441 | 0.063794 | 0.000007 | −0.000563 | 0.02 | 0.08 |
| MTSAT−1R/JAMI | 0.144507 | 0.998699 | 0.114078 | 0.000009 | −0.000970 | 0.02 | 0.07 | |
| Aqua/AIRS | MTSAT−2/IMAGER | −0.121095 | 1.002002 | 0.061224 | 0.000006 | −0.000522 | 0.04 | 0.08 |
| MTSAT−1R/JAMI | −0.292163 | 1.002461 | 0.090412 | 0.000009 | −0.000767 | −0.05 | 0.11 | |
| GOES−9/Imager | −0.284225 | 1.002409 | 0.088484 | 0.000009 | −0.000759 | −0.05 | 0.11 | |
| GMS−5/VISSR | −0.292097 | 1.002457 | 0.090624 | 0.000009 | −0.000768 | −0.05 | 0.11 | |
| NOAA−14/HIRS | MTSAT−1R/JAMI | −0.734200 | 1.005595 | 0.271737 | 0.000027 | −0.002280 | −0.15 | 0.19 |
| GOES−9/Imager | −1.034351 | 1.006135 | 0.312382 | 0.000029 | −0.002546 | −0.33 | 0.20 | |
| GMS−5/VISSR | −1.124275 | 1.006135 | 0.181406 | 0.000018 | −0.001529 | −0.38 | 0.16 | |
| GMS−4/VISSR | −1.112169 | 1.006103 | 0.179381 | 0.000018 | −0.001525 | −0.38 | 0.15 | |
| NOAA−12/HIRS | GMS−5/VISSR | −1.311274 | 1.008521 | 0.285484 | 0.000029 | −0.002467 | −0.36 | 0.19 |
| GMS−4/VISSR | −1.401261 | 1.010117 | 0.368249 | 0.000039 | −0.003387 | −0.33 | 0.18 | |
| NOAA−11/HIRS | GMS−5/VISSR | −1.111511 | 1.006030 | 0.325626 | 0.000032 | −0.002699 | −0.38 | 0.21 |
| GMS−4/VISSR | −1.263044 | 1.007409 | 0.530304 | 0.000057 | −0.004964 | −0.40 | 0.22 | |
| GMS−3/VISSR | −1.207011 | 1.006175 | 0.592163 | 0.000058 | −0.005270 | −0.40 | 0.22 | |
| NOAA−10/HIRS | GMS−4/VISSR | −1.202206 | 1.007659 | 0.713625 | 0.000078 | −0.006757 | −0.34 | 0.25 |
| GMS−3/VISSR | −1.251572 | 1.008905 | 0.909150 | 0.000090 | −0.007954 | −0.25 | 0.30 | |
| NOAA−09/HIRS | GMS−3/VISSR | −1.355845 | 1.006734 | 1.559957 | 0.000146 | −0.013390 | −0.46 | 0.38 |
| NOAA−08/HIRS | GMS−2/VISSR | −1.522800 | 1.011568 | 3.940222 | 0.000419 | −0.035527 | −0.31 | 0.65 |
| GMS/VISSR | −1.951627 | 1.016254 | 3.261468 | 0.000311 | −0.027537 | −0.25 | 0.61 | |
| NOAA−07/HIRS | GMS−3/VISSR | −2.082845 | 1.015993 | 2.371047 | 0.000210 | −0.018764 | −0.35 | 0.55 |
| GMS−2/VISSR | −2.019434 | 1.016222 | 2.181436 | 0.000210 | −0.017886 | −0.36 | 0.55 | |
| GMS/VISSR | −2.084215 | 1.016094 | 2.352383 | 0.000210 | −0.018685 | −0.35 | 0.55 | |
| NOAA−06/HIRS | GMS−2/VISSR | −2.113411 | 1.015869 | 3.515013 | 0.000352 | −0.029636 | −0.44 | 0.69 |
| GMS/VISSR | −2.106854 | 1.016738 | 3.321103 | 0.000291 | −0.026619 | −0.32 | 0.62 | |
| TIROS−N/HIRS | GMS/VISSR | −2.297130 | 1.017590 | 4.171134 | 0.000366 | −0.034199 | −0.39 | 0.65 |
| LEO Instrument | SRF of GEO | offsetprime | slopeprime | var (offsetprime) | var (slopeprime) | cov(offsetprime,slopeprime) | corr. vol. at Standard Radiance [K] | corr. uncert. at Standard Radiance [K] |
|---|---|---|---|---|---|---|---|---|
| Metop−B/IASI | MTSAT−2/IMAGER | 0.003085 | 0.999110 | 0.000377 | 0.000007 | −0.000043 | −0.01 | 0.05 |
| MTSAT−1R/JAMI | 0.003887 | 0.999501 | 0.000466 | 0.000007 | −0.000053 | 0.01 | 0.06 | |
| Aqua/AIRS | MTSAT−2/IMAGER | −0.018678 | 1.000531 | 0.000447 | 0.000007 | −0.000044 | −0.08 | 0.07 |
| MTSAT−1R/JAMI | −0.035988 | 1.000722 | 0.000592 | 0.000011 | −0.000068 | −0.17 | 0.07 | |
| GOES−9/Imager | −0.036051 | 1.000669 | 0.000605 | 0.000011 | −0.000069 | −0.17 | 0.07 | |
| GMS−5/VISSR | 0.101970 | 0.982413 | 0.001490 | 0.000014 | −0.000126 | −0.10 | 0.08 | |
| NOAA−14/HIRS | MTSAT−1R/JAMI | 0.016325 | 1.024467 | 0.002230 | 0.000050 | −0.000298 | 0.73 | 0.12 |
| GOES−9/Imager | −0.044988 | 1.033843 | 0.002244 | 0.000056 | −0.000313 | 0.66 | 0.12 | |
| GMS−5/VISSR | 0.171770 | 0.981978 | 0.027306 | 0.000332 | −0.002588 | 0.17 | 0.34 | |
| NOAA−12/HIRS | GMS−5/VISSR | 0.116263 | 0.984391 | 0.062003 | 0.000778 | −0.006282 | 0.02 | 0.44 |
| NOAA−11/HIRS | GMS−5/VISSR | 0.076281 | 0.989298 | 0.075076 | 0.000847 | −0.007161 | 0.00 | 0.50 |
References
- Yang, J.; Gong, P.; Fu, R.; Zhang, M.; Chen, J.; Liang, S.; Xu, B.; Shi, J.; Dickinson, R. The role of satellite remote sensing in climate change studies. Nat. Clim. Chang. 2013, 3, 875–883. [Google Scholar] [CrossRef]
- Dowell, M.; Lecomte, P.; Husband, R.; Schulz, J.; Mohr, T.; Tahara, Y.; Eckman, R.; Lindstrom, E.; Wooldridge, C.; Hilding, S.; et al. Strategy Towards an Architecture for Climate Monitoring from Space. 2013. Available online: http://www.wmo.int/pages/prog/sat/documents/ARCH_strategy-climate-architecture-space.pdf (accessed on 1 March 2019).
- Meirink, J.F.; Roebeling, R.A.; Stammes, P. Inter-calibration of polar imager solar channels using SEVIRI. Atmos. Meas. Tech. 2013, 6, 2495–2508. [Google Scholar] [CrossRef] [Green Version]
- Cao, C.; Xiong, X.; Wu, A.; Wu, X. Assessing the consistency of AVHRR and MODIS L1B reflectance for generating fundamental climate data records. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Wang, L.; Cao, C.; Ciren, P. Assessing NOAA-16 HIRS Radiance Accuracy Using Simultaneous Nadir Overpass Observations from AIRS. J. Atmos. Ocean. Technol. 2007, 24. [Google Scholar] [CrossRef]
- Cao, C.; Weinreb, M.; Xu, H. Predicting simultaneous nadir overpasses among polar-orbiting meteorological satellites for the intersatellite calibration of radiometers. J. Atmos. Ocean. Technol. 2004, 21, 537–542. [Google Scholar] [CrossRef]
- Goldberg, M.; Ohring, G.; Butler, J.; Cao, C.; Datla, R.; Doelling, D.; Gaertner, V.; Hewison, T.; Iacovazzi, B.; Kim, D.; et al. The global space-based inter-calibration system (GSICS). Bull. Am. Meteorol. Soc. 2011, 92, 468–475. [Google Scholar] [CrossRef]
- Okuyama, A.; Hashimoto, T.; Nakayama, R.; Tahara, Y.; Kurino, T.; Takenaka, H.; Fukuda, S.; Nakajima, T.Y.; Higurashi, A.; Sekiguchi, M.; et al. Geostationary Imager Visible Channel Recalibration. In Proceedings of the 2009 Eumetsat Meteorological Satellite Conference, Session 6, Bath, UK, 21–25 September 2009; Monitoring Climate and Understanding Climate Processes with Satellites. ISBN 978-92-9110-086-6. [Google Scholar]
- Sasaki, H. Reproduction of GMS IR calibration table. Meteorol. Satell. Center Tech. Note 1988, 17, 9–13. [Google Scholar]
- John, V.O.; Tabata, T.; Rüthrich, F.; Roebeling, R.; Hewison, T.; Stöckli, R.; Schulz, J. On the Methods for Recalibrating Geostationary Longwave Channels Using Polar Orbiting Infrared Sounders. Remote Sens. 2019, 11, 1171. [Google Scholar] [CrossRef]
- Hewison, T.J.; Wu, X.; Yu, F.; Tahara, Y.; Hu, X.; Kim, D.; Koenig, M. GSICS Inter-Calibration of Infrared Channels of Geostationary Imagers Using Metop/IASI. IEEE Trans. Geosci. Remote Sens. 2013, 51, 1160–1170. [Google Scholar] [CrossRef]
- SCOPE-CM. SCOPE-CM Phase 2 Implementation Plan. Version 1.0. 2012. Available online: http://www.scope-cm.org/wpcms/wp-content/uploads/2014/01/SCOPE-CM_Phase-2-Implementation-Plan.pdf (accessed on 8 August 2018).
- JMA. The History of Meteorological Satellites at JMA. Available online: https://www.jma.go.jp/jma/jma-eng/satellite/introduction/history.html (accessed on 28 August 2018).
- NOAA. GOES Imager Instrument. Available online: http://noaasis.noaa.gov/NOAASIS/ml/imager.html (accessed on 28 August 2018).
- Space Systems Loral. GOES I-M DataBook. 31 August 1996. Available online: https://goes.gsfc.nasa.gov/text/databook/databook.pdf (accessed on 28 August 2018).
- Shirakawa, Y.; Sasaki, M. Characteristics of GMS-4 VISSR. Meteorol. Satell. Center Tech. Note 1990, 21, 1–10. (In Japanese) [Google Scholar]
- Uchiyama, A. GMS Operational Calibration Procedure and Status. Meteorol. Satell. Center Tech. Note 1984, 10, 85–92. [Google Scholar]
- JMA. 2017: Algorithm Theoretical Basis Document (ATBD) for GSICS Infrared Inter-Calibration of Imagers on MTSAT-1R/-2 and Himawari-8/-9 using AIRS and IASI Hyperspectral Observations. Dec. 2017, Ver. 1.1. Available online: https://www.data.jma.go.jp/mscweb/data/monitoring/gsics/ir/ATBD_for_JMA_Demonstration_GSICS_Inter-Calibration_of_MTSAT_Himawari-AIRSIASI.pdf (accessed on 8 August 2018).
- Tahara, Y. Central Wavelengths and Wavenumbers and Sensor Planck Functions of the GMS and MTSAT Infrared Channels. Meteorol. Satell. Center Tech. Note 2008, 50, 51–59. (In Japanese) [Google Scholar]
- Meteorological Satellite Center, Japan Meteorological Agency. THE GMS USER’S GUIDE Third Edition. Available online: https://www.data.jma.go.jp/mscweb/en/operation/docs/GMS_Users_Guide_3rd_Edition_Rev1.pdf (accessed on 5 November 2013).
- Tsuchiya, K.; Tokuno, M.; Itaya, H.; Sasaki, H. Calibration of GMS-VISSR, features of MOS-VTIR and Landsat MSS. Adv. Space Res. 1996, 17, 1–10. [Google Scholar] [CrossRef]
- Bréon, F.M.; Jackson, D. Evidence of Atmospheric Contamination on the Measurement of the Spectral Response of the GMS-5 Water Vapor Channel. J. Atmos. Oceanic. Technol. 1999, 16, 1851–1853. [Google Scholar] [CrossRef]
- Kobayashi, S.; Oyama, R.; Shimoji, K.; Uesawa, D.; Imai, T.; Okuyama, A.; Harada, Y.; Moriya, M.; Yasui, S.; Onogi, K.; et al. Slides for the 4th World Climate Research Program International Conference on Reanalyzes. Available online: https://www.wcrp-climate.org/ICR4/ppts/Kobayashi.pdf (accessed on 5 November 2013).


















| Satellite | Operational Period (DD/MM/YYYY) | Sensor | File Format | Channels Recalibrated in This Study | Calibration Table | Bit Depth | Note |
|---|---|---|---|---|---|---|---|
| GMS | 06/04/1978–21/12/1981 21/01/1984–29/06/1984 | VISSR | VISSR | IR | Not fixed | 8 bits | |
| GMS-2 | 21/12/1981–21/01/1984 29/06/1984–27/11/1984 | VISSR | VISSR | IR | Not fixed | 8 bits | |
| GMS-3 | 27/11/1984–14/12/1989 | VISSR | VISSR | IR | Not fixed | 8 bits | |
| GMS-4 | 14/12/1989–13/06/1995 | VISSR | VISSR | IR | Not fixed | 8 bits | |
| GMS-5 | 13/06/1995–22/05/2003 | VISSR | VISSR | IR/WV | Not fixed | 8 bits | |
| GOES-9 (backup-period) | 22/05/2003–01/07/2005 | Imager | VISSR | IR/WV | Fixed | 8 bits | Due to MTSAT launch failure, GOES-9 was moved to the West Pacific Ocean and was jointly operated by JMA and NOAA. |
| MTSAT-1R | 01/07/2005– 04/06/2007 06/06/2007–17/02/2009 18/02/2009–11/11/2009 12/11/2009–16/11/2009 27/11/2009–01/07/2010 07/10/2010–22/12/2010 03/08/2011–16/08/2011 01/11/2011–26/12/2011 18/10/2012 –26/12/2012 22/10/2013–19/12/2013 10/11/2014–28/11/2014 | JAMI | HRIT | IR/WV | Fixed | 10 bits | |
| MTSAT-2 | 04/06/2007–06/06/2007 17/02/2009–18/02/2009 11/11/2009–12/11/2009 16/11/2009–27/11/2009 01/07/2010–07/10/2010 22/12/2010–03/08/2011 16/08/2011–01/11/2011 26/12/2011–18/10/2012 26/12/2012–22/10/2013 19/12/2013–10/11/2014 28/11/2014–24/03/2016 | IMAGER | HRIT | IR/WV | Fixed | 10 bits | Himawari-8 began operation on 7 July 2015. MTSAT-2 parallel operation was terminated on 24 March 2016. |
| Satellite/Sensor | Available Dates (Archived Data) | Freq. Updates Operational Calibration Coefficient | Telemetry Data | Note |
|---|---|---|---|---|
| GMS/VISSR | 01/12/1978 | 01/12/1979 | 1 time/day or less (mean: 0.28 times/day) | Stored in header part of VISSR files. However, no information about sensor temperature or blackbody calibration | C = β0 + β1 V = α0E + V0 C is count, V is voltage and E is the radiance, respectively. β0, β1, V0, and α0 were daily calculated with deep space observation, blackbody observation and the staircase data offline. However, those constants for calculating operational calibration table were updated only if they were significantly different from the operational ones (by t-test). GMS/VISSR data during 01/12/1978–01/12/1979 are archived by University of Wisconsin and were provided to JMA. |
| 28/02/1981 | 29/06/1984 | 1 time/day or less (mean: 0.09 times/day) | Not stored | ||
| GMS-2/VISSR | 21/12/1981 | 27/09/1984 | 1 time/day or less (mean: 0.22 times/day) | Not stored | |
| GMS-3/VISSR | 27/09/1984 | 28/02/1987 | 1 time/day or less (mean: 0.40 times/day) | Not stored | Operational calibration process has changed on 28/02/1978 |
| 28/02/1987 | 04/12/1989 | 24 times/day or less (mean: 15.4 times /day) | Stored in header of VISSR files | Calibration coefficients were not updated soon after midnight in eclipse period for GMS-3 and GMS-4. | |
| GMS-4/VISSR | 04/12/1989 | 13/06/1995 | 24 times/day or less (mean: 22.5 times /day) | Stored in header of VISSR files | Calibration coefficients were not updated soon after midnight in eclipse period for GMS-3 and GMS-4. |
| GMS-5/VISSR | 13/06/1995 | 21/05/2003 | 24 times/day or less (mean: 23.7 times /day) | Stored in header of VISSR files |
| Sensor | Period | Satellite |
|---|---|---|
| HIRS/2 | 1978–2006 | TIROS-N, NOAA-6, NOAA-7, NOAA-8, NOAA-9, NOAA-10, NOAA-11, NOAA-12, NOAA-14 |
| AIRS | 2002–date | Aqua |
| IASI | 2006–date | Metop-A, Metop-B |
| Satellite | Channel | Condition | MaxTime (minutes) | MaxZen | MaxStd (mW/(m2 sr cm−1)) | Gaussian |
|---|---|---|---|---|---|---|
| GMS | IR | Clear | 5 | 0.01 | 3.466 | 2 |
| Cloud | 0.03 | 6.932 | ||||
| GMS-2 | IR | Clear | 5 | 0.01 | 3.536 | 2 |
| Cloud | 0.03 | 7.072 | ||||
| GMS-3 | IR | Clear | 5 | 0.01 | 3.878 | 2 |
| Cloud | 0.03 | 7.756 | ||||
| GMS-4 | IR | Clear | 5 | 0.01 | 1.609 | 2 |
| Cloud | 0.03 | 3.218 | ||||
| GMS-5 | IR | Clear | 5 | 0.01 | 1.755 | 2 |
| Cloud | 0.03 | 3.510 | ||||
| WV | All | 0.01 | 0.697 | 1 | ||
| GOES-9 | IR | Clear | 5 | 0.01 | 1.720 | 2 |
| Cloud | 0.03 | 3.440 | ||||
| WV | All | 0.01 | 0.642 | 1 | ||
| MTSAT-1R | IR | Clear | 5 | 0.01 | 1.655 | 2 |
| Cloud | 0.03 | 3.310 | ||||
| WV | All | 0.01 | 0.311 | 1 | ||
| MTSAT-2 | IR | Clear | 5 | 0.01 | 1.655 | 2 |
| Cloud | 0.03 | 3.310 | ||||
| WV | All | 0.01 | 0.311 | 1 |
| Radiance (mW/(m2 sr cm−1)) | Brightness Temperature(K) | |||
|---|---|---|---|---|
| IR Channel | WV Channel | IR Channel | WV Channel | |
| GMS | 96.373 | - | 285.43 | - |
| GMS-2 | 91.593 | - | 285.84 | - |
| GMS-3 | 96.868 | - | 285.48 | - |
| GMS-4 | 90.551 | - | 285.51 | - |
| GMS-5 | 90.853 | 7.1787 | 286.14 | 243.69 |
| GOES-9 | 89.514 | 5.0823 | 286.26 | 238.25 |
| MTSAT-1R | 90.681 | 4.9840 | 286.17 | 237.85 |
| MTSAT-2 | 91.497 | 5.3513 | 286.70 | 239.17 |
| Satellite/Sensor | WV-Operational BT Average (std) | WV-Recalibrated BT Average (std) | IR-Operational BT Average (std) | IR-Recalibrated BT Average (std) |
|---|---|---|---|---|
| GMS/VISSR | - | - | 291.19 (1.60) | 291.25 (1.04) |
| GMS-2/VISSR | - | - | 291.65 (2.34) | 290.94 (1.23) |
| GMS-3/VISSR | - | - | 291.98 (1.59) | 291.06 (1.10) |
| GMS-4/VISSR | - | - | 291.80 (1.42) | 290.87 (1.07) |
| GMS-5/VISSR | 246.44 (1.40) | 246.65 (1.42) | 290.45 (1.05) | 291.13 (1.11) |
| GOES-9/Imager | 247.75 (1.77) | 247.25 (1.75) | 291.4 (1.08) | 291.43 (1.07) |
| MTSAT-1R/JAMI | 247.55 (1.48) | 247.26 (1.48) | 290.87 (1.11) | 291.17 (1.10) |
| MTSAT-2/IMAGER | 247.07 (1.56) | 247.33 (1.56) | 290.85 (1.14) | 290.82 (1.13) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tabata, T.; John, V.O.; Roebeling, R.A.; Hewison, T.; Schulz, J. Recalibration of over 35 Years of Infrared and Water Vapor Channel Radiances of the JMA Geostationary Satellites. Remote Sens. 2019, 11, 1189. https://doi.org/10.3390/rs11101189
Tabata T, John VO, Roebeling RA, Hewison T, Schulz J. Recalibration of over 35 Years of Infrared and Water Vapor Channel Radiances of the JMA Geostationary Satellites. Remote Sensing. 2019; 11(10):1189. https://doi.org/10.3390/rs11101189
Chicago/Turabian StyleTabata, Tasuku, Viju O. John, Rob A. Roebeling, Tim Hewison, and Jörg Schulz. 2019. "Recalibration of over 35 Years of Infrared and Water Vapor Channel Radiances of the JMA Geostationary Satellites" Remote Sensing 11, no. 10: 1189. https://doi.org/10.3390/rs11101189
APA StyleTabata, T., John, V. O., Roebeling, R. A., Hewison, T., & Schulz, J. (2019). Recalibration of over 35 Years of Infrared and Water Vapor Channel Radiances of the JMA Geostationary Satellites. Remote Sensing, 11(10), 1189. https://doi.org/10.3390/rs11101189