Dynamic Harris Hawks Optimization with Mutation Mechanism for Satellite Image Segmentation
Abstract
:1. Introduction
- Introduce the recently proposed HHO into multilevel image thresholding. To the best of the authors’ knowledge, this attempt has not been made yet.
- Dynamic control parameter strategy and mutation mechanism are used to improve the search efficiency of the original HHO.
- Objectively and comprehensively evaluate the performance of the proposed technique.
2. Material and Methods
2.1. Problem Statement
2.2. Multilevel Thresholding
2.2.1. Kapur’s Entropy
2.2.2. Tsallis Entropy
2.2.3. Otsu Between-Class Variance
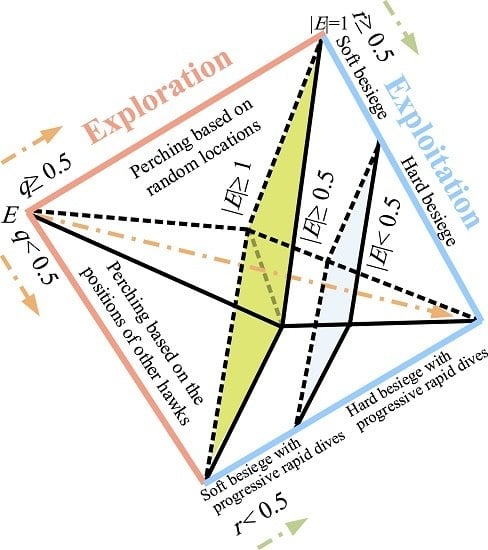
2.3. Harris Hawks Optimization
2.3.1. Exploration Stage
2.3.2. Transition from Exploration to Exploitation
2.3.3. Exploitation Stage
| Algorithm 1 Pseudocode of Harris hawks optimization (HHO) algorithm |
| Input: The size of population , maximum number of iterations . Output: The position of the rabbit and the corresponding fitness function value.
|
2.4. Proposed Dynamic Harris Hawks Optimization with Mutation Mechanism
2.4.1. Dynamic Control Parameter Strategy
2.4.2. Mutation Mechanism
2.4.3. Algorithm Steps
| Algorithm 2 Pseudocode of dynamic Harris hawks optimization with a mutation mechanism (DHHO/M) based multilevel color image thresholding |
| Input: The given color image. |
| Output: Segmentation thresholds. |
| 24. Read the given color image. |
| 25. Extract the histogram of each color component (R, G, and B). |
| 26. Initialize the position of the hawks and the rabbit . |
| 27. Initialize the fitness values of the hawks and the rabbit . |
| 28. Set population size and maximum number of iterations . |
| 29. Set the dimensions of the optimization problem , namely the number of thresholds. |
| 30. While (termination condition is not met ) do |
| 31. Check the boundary and evaluate the fitness value of each hawk using Equations (4)–(6). |
| 32. Update the location and fitness value of rabbit if there is a better one. |
| 33. For (each hawk )) do |
| 34. Update the energy of the rabbit using Equation (21). % Dynamic control parameter strategy |
| 35. If () then |
| 36. Update the position using Equation (23). % Mutation mechanism |
| 37. Else If () then |
| 38. If () then |
| 39. Update the position using Equation (10). |
| 40. Else If () then |
| 41. Update the position using Equation (12). |
| 42. Else If () then |
| 43. Update the position using Equation (16). |
| 44. Else If () then |
| 45. Update the position using Equation (17). |
| 46. End If |
| 47. End If |
| 48. End For |
| 49. End While |
| Fitness function (Kapur’s entropy) |
| Input: Histogram of a color component, and segmentation thresholds . |
| Output: Fitness function value . |
|
2.4.4. Computational Complexity
3. Discussions
3.1. Experimental Setup and Database
3.2. Performance Metrics.
3.3. Experimental Series 1: Performance on Mathematical Functions
3.4. Experimental Series 2: Influence of Dynamic Control Parameter Strategy and Mutation Mechanism
3.5. Experimental Series 3: Comparison with Other Advanced Methods on Satellite Images
3.5.1. Segmentation Accuracy
3.5.2. Statistical Test
3.5.3. Computational Time
3.5.4. Search Capability on High Dimensional Problems
3.5.5. Stability Analysis
3.5.6. Convergence Property
3.6. Experimental Series 4: Performance Using Different Objective Functions
3.7. Experimental Series 5: Oil Pollution Image Segmentation
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Frongillo, M.; Gennarelli, G.; Riccio, G. Plane Wave Diffraction by Arbitrary-Angled Lossless Wedges: High Frequency and Time Domain Solutions. IEEE Trans. Antennas Propag. 2018, 66, 6646–6653. [Google Scholar] [CrossRef]
- Hinojosa, S.; Avalos, O.; Oliva, D.; Cuevas, E.; Pajares, G.; Zaldivar, D.; Gálvez, J. Unassisted thresholding based on multi-objective evolutionary algorithms. Knowl. Based Syst. 2018, 159, 221–232. [Google Scholar] [CrossRef]
- Guido, R.C.; Addison, P.; Walker, J. Introducing wavelets and time-frequency analysis. IEEE Eng. Biol. Med. Mag. 2009, 28, 13. [Google Scholar] [CrossRef]
- Guido, R.C. Practical and useful tips on discrete wavelet transforms. IEEE Signal Process. Mag. 2015, 32, 162–166. [Google Scholar] [CrossRef]
- Mallat, S.G. A Theory for Multiresolution Signal Decomposition: The Wavelet Representation. IEEE Trans. Pattern Anal. Mach. Intell. 1989, 2, 674–693. [Google Scholar] [CrossRef]
- Guariglia, E. Entropy and Fractal Antennas. Entropy 2016, 18, 84. [Google Scholar] [CrossRef]
- Khairuzzaman, A.K.M.; Chaudhury, S. Multilevel thresholding using grey wolf optimizer for image segmentation. Expert Syst. Appl. 2017, 86, 64–76. [Google Scholar] [CrossRef]
- Hinojosa, S.; Dhal, K.G.; Elaziz, M.A.; Oliva, D.; Cuevas, E. Entropy-based imagery segmentation for breast histology using the Stochastic Fractal Search. Neurocomputing 2018, 321, 201–215. [Google Scholar] [CrossRef]
- Oliva, D.; Cuevas, E.; Pajares, G.; Zaldivar, D.; Osuna, V. A Multilevel Thresholding algorithm using electromagnetism optimization. Neurocomputing 2014, 139, 357–381. [Google Scholar] [CrossRef] [Green Version]
- Aziz, M.A.E.; Ewees, A.A.; Hassanien, A.E. Whale Optimization Algorithm and Moth-Flame Optimization for multilevel thresholding image segmentation. Expert Syst. Appl. 2017, 83, 242–256. [Google Scholar] [CrossRef]
- He, L.; Huang, S. Modified firefly algorithm based multilevel thresholding for color image segmentation. Neurocomputing 2017, 240, 152–174. [Google Scholar] [CrossRef]
- Díaz-Cortés, M.; Ortega-Sánchez, N.; Hinojosa, S.; Oliva, D.; Cuevas, E.; Rojas, R.; Demin, A. A multi-level thresholding method for breast thermograms analysis using Dragonfly algorithm. Infrared Phys. Technol. 2018, 93, 346–361. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Modified artificial bee colony based computationally efficient multilevel thresholding for satellite image segmentation using Kapur’s, Otsu and Tsallis functions. Expert Syst. Appl. 2015, 42, 1573–1601. [Google Scholar] [CrossRef]
- Kapura, J.N.; Sahoob, P.K.; Wongc, A.K.C. A new method for gray-level picture thresholding using the entropy of the histogram. Comput. Vis. Graph. Image Proc. 1985, 29, 273–285. [Google Scholar] [CrossRef]
- Tsallis, C. Possible generalization of Boltzmann–Gibbs statistics. J. Stat. Phys. 1988, 52, 479–487. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Oliva, D.; Hinojosa, S.; Cuevas, E.; Pajares, G.; Avalos, O.; Gálvez, J. Cross entropy based thresholding for magnetic resonance brain images using Crow Search Algorithm. Expert Syst. Appl. 2017, 79, 164–180. [Google Scholar] [CrossRef]
- Lang, C.; Jia, H. Kapur’s Entropy for Color Image Segmentation Based on a Hybrid Whale Optimization Algorithm. Entropy 2019, 21, 318. [Google Scholar] [CrossRef]
- Jia, H.; Peng, X.; Song, W.; Lang, C.; Xing, Z.; Sun, K. Multiverse Optimization Algorithm Based on Lévy Flight Improvement for Multithreshold Color Image Segmentation. IEEE Access 2019. [Google Scholar] [CrossRef]
- Liang, H.; Jia, H.; Xing, Z.; Ma, J.; Peng, X. Modified Grasshopper Algorithm-Based Multilevel Thresholding for Color Image Segmentation. IEEE Access 2019, 7, 11258–11295. [Google Scholar] [CrossRef]
- Ouadfel, S.; Taleb-Ahmed, A. Social spiders optimization and flower pollination algorithm for multilevel image thresholding: A performance study. Expert Syst. Appl. 2016, 55, 566–584. [Google Scholar] [CrossRef]
- Beevi K., S.; Nair, M.S.; Bindu, G.R. Automatic segmentation of cell nuclei using Krill Herd optimization based multi-thresholding and Localized Active Contour Model. Biocybern. Biomed. Eng. 2016, 36, 584–596. [Google Scholar] [CrossRef]
- Pare, S.; Kumar, A.; Bajaj, V.; Singh, G.K. An efficient method for multilevel color image thresholding using cuckoo search algorithm based on minimum cross entropy. Appl. Soft Comput. 2017, 61, 570–592. [Google Scholar] [CrossRef]
- Pare, S.; Bhandari, A.K.; Kumar, A.; Singh, G.K. A new technique for multilevel color image thresholding based on modified fuzzy entropy and Lévy flight firefly algorithm. Comput. Electr. Eng. 2018, 70, 476–495. [Google Scholar] [CrossRef]
- Mlakar, U.; Potočnik, B.; Brest, J. A hybrid differential evolution for optimal multilevel image thresholding. Expert Syst. Appl. 2016, 65, 221–232. [Google Scholar] [CrossRef]
- Kotte, S.; Pullakura, R.K.; Injeti, S.K. Optimal multilevel thresholding selection for brain MRI image segmentation based on adaptive wind driven optimization. Measurement 2018, 130, 340–361. [Google Scholar] [CrossRef]
- Wolpert, D.H.; Macready, W.G. No free lunch theorems for optimization. Evolut. Comput. IEEE Trans. 1997, 1, 67–82. [Google Scholar] [CrossRef] [Green Version]
- Heidari, A.A.; Mirjalili, S.; Faris, H.; Aljarah, I.; Mafarja, M.; Chen, H. Harris hawks optimization: Algorithm and applications. Future Gener. Comput. Syst. 2019, 97, 849–872. [Google Scholar] [CrossRef]
- Das, S.; Mullick, S.S.; Suganthan, P.N. Recent advances in differential evolution—An updated survey. Swarm Evol. Comput. 2016, 27, 1–30. [Google Scholar] [CrossRef]
- Bhandari, A.K.; Kumar, A.; Singh, G.K. Tsallis entropy based multilevel thresholding for colored satellite image segmentation using evolutionary algorithms. Expert Syst. Appl. 2015, 42, 8707–8730. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Oliva, D.; Ewees, A.A.; Xiong, S. Multi-level thresholding-based grey scale image segmentation using multi-objective multi-verse optimizer. Expert Syst. Appl. 2019, 125, 112–129. [Google Scholar] [CrossRef]
- Agrawal, S.; Panda, R.; Bhuyan, S.; Panigrahi, B.K. Tsallis entropy based optimal multilevel thresholding using cuckoo search algorithm. Swarm Evol. Comput. 2013, 11, 16–30. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Yuan, X.; Shi, D.; He, Y.; Yao, G. Parameter extraction of solar photovoltaic models by means of a hybrid differential evolution with whale optimization algorithm. Sol. Energy 2018, 176, 742–761. [Google Scholar] [CrossRef]
- Jadon, S.S.; Tiwari, R.; Sharma, H.; Bansal, J.C. Hybrid Artificial Bee Colony algorithm with Differential Evolution. Appl. Soft Comput. 2017, 58, 11–24. [Google Scholar] [CrossRef]
- Elaziz, M.A.; Xiong, S.; Jayasena, K.P.N.; Li, L. Task scheduling in cloud computing based on hybrid moth search algorithm and differential evolution. Knowl. Based Syst. 2019, 169, 39–52. [Google Scholar] [CrossRef]
- Xiong, G.; Zhang, J.; Shi, D.; He, Y. Parameter extraction of solar photovoltaic models using an improved whale optimization algorithm. Energy Convers. Manag. 2018, 174, 388–405. [Google Scholar] [CrossRef]
- Zhao, F.; Xue, F.; Zhang, Y.; Ma, W.; Zhang, C.; Song, H. A hybrid algorithm based on self-adaptive gravitational search algorithm and differential evolution. Expert Syst. Appl. 2018, 113, 515–530. [Google Scholar] [CrossRef]
- Xu, L.; Jia, H.; Lang, C.; Peng, X.; Sun, K. A Novel Method for Multilevel Color Image Segmentation Based on Dragonfly Algorithm and Differential Evolution. IEEE Access 2019, 7, 19502–19538. [Google Scholar] [CrossRef]
- Gao, W.; Huang, L.; Wang, J.; Liu, S.; Qin, C. Enhanced artificial bee colony algorithm through differential evolution. Appl. Soft Comput. 2016, 48, 137–150. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Elaziz, M.A.; Lu, S. Chaotic opposition-based grey-wolf optimization algorithm based on differential evolution and disruption operator for global optimization. Expert Syst. Appl. 2018, 108, 1–27. [Google Scholar] [CrossRef]
- Xu, Y.; Chen, H.; Luo, J.; Zhang, Q.; Jiao, S.; Zhang, X. Enhanced Moth-flame optimizer with mutation strategy for global optimization. Inf. Sci. 2019, 492, 181–203. [Google Scholar] [CrossRef]
- Hijime, K.; Isao, O.; Shingenobu, K. Theoretical Analysis of the Unimodal Normal Distribution Crossover for Real-coded Genetic Algorithms. Trans. Soc. Instrum. Control Eng. 2002, 2, 187–194. [Google Scholar]
- Akimoto, Y.; Nagata, Y.; Sakuma, J.; Ono, I.; Kobayashi, S. Proposal and evaluation of adaptive real-coded crossover AREX. Trans. Jpn. Soc. Artif. Intell. 2009, 24, 446–458. [Google Scholar] [CrossRef]
- Ariyarit, A.; Kanazaki, M. Multi-modal distribution crossover method based on two crossing segments bounded by selected parents applied to multi-objective design optimization. J. Mech. Sci. Technol. 2015, 29, 1443–1448. [Google Scholar] [CrossRef]
- Eshelman, L.J.; Schaffer, J.D. Real-Coded Genetic Algorithms and Interval-Schemata, Foundations of Genetic Algorithms 2; Morgan Kaufman Publisher: San Mateo, CA, USA, 1993; pp. 187–202. [Google Scholar] [CrossRef]
- Jia, H.; Lang, C.; Oliva, D.; Song, W.; Peng, X. Hybrid Grasshopper Optimization Algorithm and Differential Evolution for Multilevel Satellite Image Segmentation. Remote Sens. 2019, 11, 1134. [Google Scholar] [CrossRef]
- Gill, H.S.; Khehra, B.S.; Singh, A.; Kaur, L. Teaching-learning-based optimization algorithm to minimize cross entropy for Selecting multilevel threshold values. Egypt. Inf. J. 2019, 20, 11–25. [Google Scholar] [CrossRef]
- Bohat, V.K.; Arya, K.V. A new heuristic for multilevel thresholding of images. Expert Syst. Appl. 2019, 117, 176–203. [Google Scholar] [CrossRef]
- Kotte, S.; Kumar, P.R.; Injeti, S.K. An efficient approach for optimal multilevel thresholding selection for gray scale images based on improved differential search algorithm. Ain Shams Eng. J. 2018, 9, 1043–1067. [Google Scholar] [CrossRef] [Green Version]
- Bhandari, A.K. A novel beta differential evolution algorithm-based fast multilevel thresholding for color image segmentation. Neural Comput. Appl. 2018, 1–31. [Google Scholar] [CrossRef]
- Landsat Imagery Courtesy of NASA Goddard Space Flight Center and U.S. Geological Survey. Available online: https://landsat.visibleearth.nasa.gov/index.php?&p=1 (accessed on 7 October 2018).
- Ewees, A.A.; Elaziz, M.A.; Oliva, D. Image segmentation via multilevel thresholding using hybrid optimization algorithms. J. Electron. Imaging 2018, 27. [Google Scholar] [CrossRef]
- Shen, L.; Fan, C.; Huang, X. Multi-Level Image Thresholding Using Modified Flower Pollination Algorithm. IEEE Access 2018, 6, 30508–30519. [Google Scholar] [CrossRef]
- Frank, W. Individual Comparisons of Grouped Data by Ranking Methods. J. Econ. Entomol. 1946, 39, 269–270. [Google Scholar]
- Friedman, M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance. J. Am. Stat. Assoc. 1937, 32, 676–701. [Google Scholar] [CrossRef]
- Derrac, J.; García, S.; Molina, D.; Herrera, F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011, 1, 3–18. [Google Scholar] [CrossRef]
- Mousavirad, S.J.; Ebrahimpour-Komleh, H. Multilevel image thresholding using entropy of histogram and recently developed population-based metaheuristic algorithms. Evol. Intell. 2017, 10, 45–75. [Google Scholar] [CrossRef]
- Jia, H.; Xing, Z.; Song, W. Three Dimensional Pulse Coupled Neural Network Based on Hybrid Optimization Algorithm for Oil Pollution Image Segmentation. Remote Sens. 2019, 11, 1046. [Google Scholar] [CrossRef]














| 89 | 41 | 20 | 43 | 109 | |
| 80 | 19 | 9 | 36 | 112 | |
| 92 | 65 | 60 | 70 | 115 |
| No. | Algorithm | Parameter Setting | Year | Reference |
|---|---|---|---|---|
| 1. | DHHO/M | — | — | |
| 2. | DHHO | — | — | |
| 3. | HHO/M | — | — | |
| 4. | HHO | 2019 | [28] | |
| 5. | TLBO | 2019 | [47] | |
| 6. | WOA-TH | 2019 | [48] | |
| 7. | IDSA | — | 2018 | [49] |
| 8. | BDE | 2018 | [52] | |
| 9. | MGOA | 2019 | [20] | |
| 10. | MABC | 2015 | [13] | |
| 11. | MFPA | 2018 | [53] | |
| 12. | GWO | 2017 | [7] |
| No. | Measures | Formulation | Reference |
|---|---|---|---|
| 1. | Average fitness function value | [40] | |
| 2. | Standard deviation (Std) | [46] | |
| 3. | Peak signal to noise ratio (PSNR) | [18] | |
| 4. | Mean squared error (MSE) | [18] | |
| 5. | Structural similarity index (SSIM) | [53] | |
| 6. | Feature similarity index (FSIM) | [23] | |
| 7. | Average computation time | [17] | |
| 8. | Wilcoxon’s rank sum test | [54] | |
| 9. | Friedman test | [55] |
| F | DHHO/M | HHO | TLBO | WOA-TH | IDSA | BDE | |
|---|---|---|---|---|---|---|---|
| F1 | Best | 6.6218 × 10−120 | 5.311 × 10−106 | 54.9103 | 1.4639 | 3.4749 × 103 | 2.7038 × 10−7 |
| Mean | 2.7498 × 10−105 | 1.7563 × 10−88 | 4.7014 × 102 | 2.6078 | 1.0831 × 104 | 9.2519 × 10−6 | |
| Worst | 5.2688 × 10−97 | 5.2688 × 10−87 | 1.4603 × 103 | 3.5383 | 2.1372 × 104 | 4.5017 × 10−5 | |
| Std | 3.1671 × 10−91 | 9.6195 × 10−88 | 3.1022 × 102 | 0.45694 | 3.8111 × 103 | 1.1476 × 10−5 | |
| F9 | Best | 0 | 0 | 2.2902 × 102 | 1.5848 × 102 | 1.7535 × 102 | 3.1335 × 10−7 |
| Mean | 0 | 0 | 2.7583 × 102 | 2.1586 × 102 | 2.0861 × 102 | 2.1983 × 10−5 | |
| Worst | 0 | 0 | 3.1682 × 102 | 2.8732 × 102 | 2.4096 × 102 | 1.597 × 10−4 | |
| Std | 0 | 0 | 23.3213 | 36.1926 | 16.7857 | 3.7214 × 10−5 | |
| F14 | Best | 0.998 | 0.998 | 0.998 | 0.998 | 0.998 | 1.0311 |
| Mean | 1.069 | 1.6254 | 1.3612 | 1.1624 | 2.2329 | 1.992 | |
| Worst | 2.8008 | 5.9288 | 5.9288 | 5.9288 | 19.2307 | 0.1815 | |
| Std | 0.33043 | 1.4981 | 1.5979 | 0.90024 | 3.4264 | 1.3037 | |
| Image | K | DHHO/M | DHHO | HHO/M | HHO | DHHO+ | DHHO− | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| 1 | 2 | 12.6254 | 0 | 12.6253 | 1.00 × 10−4 | 12.6254 | 0 | 12.6253 | 1.00 × 10−4 | 12.6253 | 8.46 × 10−5 | 12.6217 | 8.20 × 10−3 |
| 3 | 15.9977 | 1.40 × 10−3 | 15.9990 | 1.70 × 10−3 | 15.9990 | 1.40 × 10−3 | 15.9971 | 1.70 × 10−3 | 15.9984 | 1.80 × 10−3 | 15.9981 | 1.40 × 10−3 | |
| 4 | 19.1537 | 0 | 19.1537 | 0 | 19.1537 | 0 | 19.1537 | 0 | 19.1537 | 0 | 19.1537 | 0 | |
| 5 | 22.0256 | 2.00 × 10−4 | 22.0254 | 1.00 × 10−4 | 22.0254 | 2.00 × 10−4 | 22.0253 | 5.60 × 10−5 | 22.0254 | 2.00 × 10−4 | 22.0254 | 2.00 × 10−4 | |
| 3 | 2 | 12.6999 | 0 | 12.6999 | 0 | 12.6999 | 0 | 12.6999 | 0 | 12.6999 | 0 | 12.6999 | 0 |
| 3 | 15.8400 | 1.30 × 10−3 | 15.8400 | 1.30 × 10−3 | 15.8400 | 1.30 × 10−3 | 15.8400 | 1.60 × 10−3 | 15.8400 | 1.30 × 10−3 | 15.8400 | 1.30 × 10−3 | |
| 4 | 18.9080 | 0 | 18.9080 | 8.45 × 10−5 | 18.9081 | 2.00 × 10−4 | 18.9080 | 1.00 × 10−4 | 18.9080 | 1.54 × 10−5 | 18.9080 | 2.00 × 10−4 | |
| 5 | 21.6937 | 2.16 × 10−5 | 21.6589 | 4.75 × 10−2 | 21.6936 | 2.00 × 10−4 | 21.6936 | 3.07 × 10−5 | 21.6936 | 0.0001 | 21.6936 | 1.00 × 10−4 | |
| 5 | 2 | 12.2672 | 0 | 12.2672 | 0 | 12.2672 | 0 | 12.2672 | 0 | 12.2672 | 0 | 12.2672 | 0 |
| 3 | 15.2240 | 1.99 × 10−2 | 15.2388 | 3.38 × 10−2 | 15.2388 | 1.00 × 10−3 | 15.2089 | 1.71 × 10−2 | 15.2314 | 1.63 × 10−2 | 15.2089 | 1.71 × 10−2 | |
| 4 | 18.0756 | 9.90 × 10−5 | 18.0676 | 1.82 × 10−2 | 18.0675 | 1.81 × 10−2 | 18.0599 | 3.02 × 10−2 | 18.0757 | 1.00 × 10−4 | 18.0676 | 1.82 × 10−2 | |
| 5 | 20.7387 | 1.88 × 10−2 | 20.7071 | 5.48 × 10−2 | 20.6817 | 5.05 × 10−2 | 20.7265 | 3.01 × 10−2 | 20.7277 | 3.17 × 10−2 | 20.6692 | 4.47 × 10−2 | |
| 7 | 2 | 12.4226 | 0 | 12.4226 | 0 | 12.4226 | 0 | 12.4226 | 0 | 12.4226 | 0 | 12.4226 | 0 |
| 3 | 15.4792 | 1.99 × 10−9 | 15.4792 | 1.99 × 10−9 | 15.4790 | 1.99 × 10−9 | 15.4792 | 1.99 × 10−9 | 15.4790 | 1.99 × 10−9 | 15.4790 | 1.99 × 10−9 | |
| 4 | 18.3182 | 1.95 × 10−5 | 18.3181 | 5.07 × 10−5 | 18.3181 | 1.95 × 10−5 | 18.3181 | 3.19 × 10−5 | 18.3181 | 2.38 × 10−5 | 18.3181 | 1.95 × 10−5 | |
| 5 | 21.0501 | 3.37 × 10−5 | 21.0499 | 3.00 × 10−4 | 21.03316 | 3.74 × 10−2 | 21.0500 | 2.00 × 10−4 | 21.0500 | 1.00 × 10−4 | 20.9918 | 5.51 × 10−2 | |
| Rank | 1(12) | 3(8) | 2(9) | 4(6) | 4(6) | 6(5) | |||||||
| Image | K | DHHO/M | HHO | TLBO | ||||||
| R | G | B | R | G | B | R | G | B | ||
| 1 | 2 | 58,171 | 111,189 | 117,187 | 58,171 | 111,189 | 117,187 | 58,171 | 111,189 | 117,187 |
| 3 | 56,123,188 | 48,122,192 | 42,128,191 | 56,123,188 | 48,122,192 | 42,128,191 | 56,123,188 | 48,122,192 | 85,143,203 | |
| 4 | 53,110,163,209 | 45,102,156,207 | 41,95,149,203 | 53,110,163,209 | 45,102,156,207 | 41,95,149,203 | 53,110,163,209 | 45,102,156,207 | 41,95,149,203 | |
| 5 | 45,86,130,173,213 | 44,90,133,174,216 | 37,85,129,170,210 | 42,82,126,171,213 | 44,90,133,174,216 | 37,85,130,171,210 | 42,82,126,171,213 | 44,90,133,174,216 | 37,85,129,170,210 | |
| 2 | 2 | 94,164 | 98,168 | 80,146 | 94,164 | 98,168 | 80,146 | 94,164 | 98,168 | 80,146 |
| 3 | 78,141,199 | 66,132,192 | 70,131,185 | 78,141,199 | 66,132,192 | 70,131,185 | 78,141,199 | 66,132,192 | 70,131,185 | |
| 4 | 67,120,169,217 | 57,107,152,195 | 53,102,148,200 | 67,120,169,217 | 57,107,152,195 | 56,107,154,200 | 67,120,169,217 | 57,107,152,195 | 53,102,148,200 | |
| 5 | 53,97,140,180,220 | 55,101,145,186,222 | 45,87,128,167,202 | 53,97,140,180,220 | 55,101,145,186,222 | 44,85,126,167,202 | 53,96,138,180,220 | 55,101,145,186,222 | 44,85,126,167,202 | |
| 3 | 2 | 86,163 | 85,162 | 80,162 | 86,163 | 85,162 | 80,162 | 86,163 | 85,162 | 80,162 |
| 3 | 84,152,207 | 81,150,207 | 65,117,170 | 84,152,207 | 81,150,207 | 78,152,210 | 84,152,207 | 81,150,207 | 65,117,170 | |
| 4 | 70,117,165,216 | 69,117,166,216 | 65,114,165,218 | 70,117,165,216 | 67,115,165,216 | 65,114,165,218 | 70,117,165,216 | 69,117,166,216 | 65,114,165,218 | |
| 5 | 36,82,125,168,216 | 45,85,126,168,216 | 57,93,132,171,218 | 36,82,125,168,216 | 45,85,126,168,216 | 18,65,114,165,218 | 36,82,125,168,216 | 45,85,126,168,216 | 58,95,134,172,218 | |
| 4 | 2 | 92,179 | 96,171 | 82,146 | 92,179 | 96,171 | 82,146 | 92,179 | 96,171 | 82,146 |
| 3 | 63,120,182 | 72,118,171 | 79,137,176 | 63,120,182 | 72,118,171 | 79,137,176 | 63,120,182 | 72,118,171 | 79,137,176 | |
| 4 | 47,89,132,182 | 70,114,159,194 | 50,91,137,176 | 47,89,132,182 | 70,114,159,194 | 50,91,137,176 | 47,89,132,182 | 70,114,159,194 | 50,91,137,176 | |
| 5 | 46,87,129,176,209 | 52,88,124,164,205 | 31,66,99,142,183 | 46,87,129,176,209 | 49,86,123,164,205 | 49,90,134,162,198 | 46,87,129,176,209 | 48,85,122,164,205 | 47,91,136,164,198 | |
| 5 | 2 | 97,158 | 95,156 | 81,144 | 97,158 | 95,156 | 81,144 | 97,158 | 95,156 | 81,144 |
| 3 | 97,148,183 | 38,96,156 | 83,138,181 | 97,148,183 | 38,96,156 | 28,82,144 | 97,148,183 | 96,150,187 | 83,138,180 | |
| 4 | 74,109,150,184 | 40,96,150,187 | 28,83,138,181 | 74,109,150,184 | 38,96,150,187 | 28,83,138,181 | 78,112,150,184 | 38,96,150,187 | 28,83,138,181 | |
| 5 | 64,93,121,153,186 | 38,79,112,152,188 | 24,52,88,138,181 | 64,93,121,153,186 | 38,82,114,152,188 | 28,80,112,144,183 | 20,74,109,148,183 | 38,79,112,152,188 | 28,80,112,144,183 | |
| 6 | 2 | 74,150 | 77,152 | 80,154 | 74,150 | 77,152 | 80,154 | 74,150 | 77,152 | 80,154 |
| 3 | 62,122,183 | 68,129,187 | 72,130,187 | 62,122,183 | 68,129,187 | 72,130,187 | 62,122,183 | 68,129,187 | 72,130,187 | |
| 4 | 51,98,147,194 | 61,105,151,197 | 61,106,152,197 | 51,98,147,194 | 61,105,151,197 | 61,106,152,197 | 51,98,147,194 | 61,105,151,197 | 61,106,152,197 | |
| 5 | 49,95,143,190,228 | 61,103,148,191,228 | 58,102,148,191,227 | 49,95,143,190,228 | 61,103,148,191,228 | 58,102,148,191,227 | 50,95,145,191,230 | 61,103,148,191,228 | 60,106,152,194,227 | |
| 7 | 2 | 96,169 | 97,160 | 64,129 | 96,169 | 97,160 | 64,129 | 96,169 | 97,160 | 64,129 |
| 3 | 80,135,190 | 81,129,177 | 55,105,154 | 80,135,190 | 81,129,177 | 55,105,154 | 80,135,190 | 81,129,177 | 55,105,154 | |
| 4 | 67,113,159,204 | 69,108,148,188 | 54,101,148,197 | 68,114,159,204 | 69,108,148,188 | 54,101,148,197 | 67,113,159,204 | 69,108,148,188 | 54,101,148,197 | |
| 5 | 57,94,132,171,209 | 68,107,146,185,226 | 48,87,125,163,197 | 57,94,132,171,209 | 24,70,110,149,188 | 50,90,129,168,206 | 15,68,114,159,204 | 68,107,146,185,226 | 48,87,125,163,197 | |
| 8 | 2 | 71,197 | 111,203 | 125,168 | 71,197 | 111,203 | 126,179 | 71,197 | 111,203 | 126,179 |
| 3 | 70,138,197 | 96,150,204 | 84,132,179 | 70,138,197 | 96,150,204 | 26,86,142 | 70,138,197 | 96,150,204 | 84,132,179 | |
| 4 | 69,114,155,197 | 56,106,152,204 | 26,84,132,179 | 69,114,155,197 | 56,106,152,204 | 27,84,132,179 | 69,114,155,197 | 54,105,152,204 | 26,85,132,179 | |
| 5 | 69,111,151,189,219 | 54,97,138,171,207 | 26,82,126,163,203 | 69,111,151,189,219 | 54,97,138,171,207 | 26,82,126,163,199 | 69,111,151,189,219 | 56,105,148,189,215 | 26,82,126,163,203 | |
| Image | K | WOA-TH | IDSA | BDE | ||||||
| R | G | B | R | G | B | R | G | B | ||
| 1 | 2 | 58,171 | 111,189 | 117,187 | 58,171 | 111,189 | 117,187 | 58,171 | 111,189 | 117,187 |
| 3 | 56,123,188 | 48,122,192 | 84,142,203 | 56,123,188 | 48,122,192 | 85,143,203 | 56,123,188 | 48,122,192 | 85,143,203 | |
| 4 | 53,110,163,209 | 45,102,156,207 | 41,95,149,203 | 53,110,163,209 | 45,102,156,207 | 41,94,149,203 | 53,111,162,209 | 45,102,156,207 | 41,95,149,203 | |
| 5 | 42,82,126,171,213 | 44,90,133,174,216 | 37,85,129,170,210 | 45,86,128,171,211 | 44,90,133,174,214 | 40,89,133,172,210 | 42,82,126,171,213 | 44,90,133,174,216 | 37,85,129,170,210 | |
| 2 | 2 | 94,164 | 98,168 | 80,146 | 94,164 | 98,168 | 80,146 | 94,164 | 98,168 | 80,146 |
| 3 | 78,141,199 | 66,132,192 | 70,131,185 | 78,141,199 | 66,132,192 | 70,131,185 | 78,141,199 | 66,132,192 | 70,131,185 | |
| 4 | 67,120,169,217 | 57,107,152,195 | 57,109,154,200 | 60,109,155,199 | 57,107,152,195 | 56,107,154,200 | 67,120,169,217 | 57,107,152,195 | 53,102,148,200 | |
| 5 | 53,96,138,180,220 | 55,101,145,186,222 | 45,88,131,169,202 | 53,95,137,180,220 | 53,97,138,178,215 | 45,87,128,167,202 | 52,93,134,174,217 | 55,101,145,186,222 | 42,84,126,167,202 | |
| 3 | 2 | 86,163 | 85,162 | 80,162 | 86,163 | 85,162 | 80,162 | 86,163 | 85,162 | 80,162 |
| 3 | 84,152,207 | 81,150,207 | 65,117,170 | 84,152,207 | 81,150,207 | 78,152,210 | 84,152,207 | 81,150,207 | 65,117,170 | |
| 4 | 70,117,165,216 | 69,117,166,216 | 65,114,165,218 | 70,117,165,216 | 69,117,166,216 | 65,115,165,218 | 70,117,165,216 | 69,117,166,216 | 65,114,165,218 | |
| 5 | 36,82,125,168,216 | 45,85,126,168,216 | 58,95,134,172,218 | 34,81,123,167,216 | 45,85,126,168,216 | 58,95,133,171,218 | 36,82,125,168,216 | 45,85,126,168,216 | 58,95,134,172,218 | |
| 4 | 2 | 92,179 | 96,171 | 82,146 | 92,179 | 96,171 | 82,146 | 92,179 | 96,171 | 82,146 |
| 3 | 63,120,182 | 72,118,171 | 79,137,176 | 62,120,182 | 72,118,171 | 79,137,176 | 63,120,182 | 72,118,171 | 79,137,176 | |
| 4 | 47,89,132,182 | 71,115,164,205 | 50,91,137,176 | 62,118,176,209 | 70,114,159,194 | 50,91,137,176 | 47,89,132,182 | 70,113,158,194 | 50,91,137,176 | |
| 5 | 47,89,130,176,209 | 49,86,123,164,205 | 49,90,134,162,198 | 42,84,124,176,209 | 48,85,121,159,194 | 49,90,134,162,197 | 46,88,130,176,209 | 52,87,122,160,198 | 49,90,134,162,198 | |
| 5 | 2 | 97,158 | 95,156 | 81,144 | 97,158 | 95,156 | 81,144 | 97,158 | 95,157 | 81,144 |
| 3 | 97,148,183 | 38,96,156 | 83,138,181 | 97,148,183 | 38,96,156 | 83,138,181 | 97,148,183 | 39,96,156 | 83,138,181 | |
| 4 | 74,109,150,184 | 38,96,150,187 | 28,83,138,181 | 74,109,150,184 | 38,96,150,187 | 28,83,138,180 | 74,109,150,184 | 38,96,150,187 | 28,83,138,182 | |
| 5 | 21,78,112,150,184 | 38,82,114,152,188 | 28,80,112,144,183 | 21,78,112,150,184 | 38,79,113,151,188 | 28,80,112,144,181 | 21,74,109,150,184 | 38,79,112,152,188 | 30,83,113,156,197 | |
| 6 | 2 | 74,150 | 77,152 | 80,154 | 74,150 | 77,152 | 80,154 | 74,150 | 77,152 | 80,154 |
| 3 | 62,122,183 | 68,129,187 | 72,130,187 | 62,122,183 | 68,129,187 | 72,131,187 | 64,125,184 | 68,129,187 | 72,130,187 | |
| 4 | 51,98,147,194 | 61,105,151,197 | 61,106,152,197 | 52,99,147,194 | 61,105,151,196 | 62,107,152,198 | 51,98,147,194 | 61,105,151,197 | 61,106,152,197 | |
| 5 | 49,95,143,190,228 | 61,103,148,191,228 | 58,102,148,191,227 | 55,99,146,190,228 | 61,103,148,191,228 | 51,86,123,161,200 | 49,95,143,190,228 | 61,103,148,191,228 | 58,102,148,191,227 | |
| 7 | 2 | 96,169 | 97,160 | 64,129 | 96,169 | 97,160 | 64,129 | 96,169 | 97,160 | 64,129 |
| 3 | 80,135,190 | 81,129,177 | 55,105,154 | 80,135,190 | 81,129,177 | 55,105,154 | 80,135,190 | 81,129,177 | 55,105,154 | |
| 4 | 68,114,159,204 | 70,110,149,188 | 54,101,148,197 | 68,114,159,204 | 69,108,148,188 | 54,101,148,197 | 67,113,159,204 | 69,108,148,188 | 54,101,148,197 | |
| 5 | 57,94,132,171,209 | 68,107,146,185,226 | 50,90,129,168,206 | 58,96,134,172,211 | 68,107,146,185,226 | 48,86,124,163,197 | 57,94,132,171,209 | 68,107,146,185,226 | 48,87,125,163,197 | |
| 8 | 2 | 71,197 | 111,203 | 126,179 | 71,197 | 111,203 | 126,179 | 71,197 | 111,203 | 126,179 |
| 3 | 70,138,197 | 96,150,204 | 84,132,179 | 70,138,197 | 96,150,204 | 84,132,179 | 70,138,197 | 96,150,204 | 84,132,179 | |
| 4 | 69,114,155,197 | 56,106,152,204 | 26,84,132,179 | 69,115,157,198 | 56,106,152,204 | 79,125,163,203 | 69,114,155,197 | 56,106,152,204 | 79,120,152,193 | |
| 5 | 69,111,151,189,219 | 56,104,146,189,215 | 26,79,120,152,193 | 68,111,151,189,219 | 53,86,119,158,204 | 26,79,120,152,193 | 69,111,151,189,219 | 54,103,148,190,216 | 27,82,125,163,199 | |
| Image | K | DHHO/M | HHO | TLBO | WOA-TH | IDSA | BDE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | Mean | Std | ||
| 1 | 2 | 12.6254 | 3.68 × 10−9 | 12.6254 | 4.73 × 10−3 | 12.6254 | 3.68 × 10−9 | 12.6254 | 3.68 × 10−9 | 12.6254 | 1.20 × 10−5 | 12.6254 | 3.68 × 10−9 |
| 3 | 15.9965 | 1.31 × 10−3 | 15.9996 | 1.61 × 10−3 | 15.9996 | 1.67 × 10−3 | 15.9996 | 1.31 × 10−3 | 15.9997 | 1.52 × 10−3 | 15.9997 | 1.61 × 10−3 | |
| 4 | 19.1537 | 1.49 × 10−4 | 19.1537 | 3.86 × 10−5 | 19.1537 | 3.63 × 10−4 | 19.1537 | 3.68 × 10−9 | 19.153 | 6.46 × 10−4 | 19.1523 | 5.59 × 10−3 | |
| 5 | 22.0256 | 1.15 × 10−4 | 22.0251 | 2.11 × 10−4 | 22.0256 | 2.40 × 10−4 | 22.025 | 3.54 × 10−4 | 22.0236 | 2.26 × 10−3 | 21.9903 | 1.42 × 10−2 | |
| 2 | 2 | 12.2446 | 3.68 × 10−9 | 12.2446 | 1.61 × 10−4 | 12.2446 | 3.68 × 10−9 | 12.2446 | 3.68 × 10−9 | 12.2446 | 3.68 × 10−9 | 12.2446 | 2.78 × 10−4 |
| 3 | 15.4553 | 1.51 × 10−4 | 15.4553 | 2.03 × 10−4 | 15.4553 | 1.92 × 10−5 | 15.4553 | 2.03 × 10−4 | 15.4553 | 9.03 × 10−4 | 15.4553 | 4.76 × 10−3 | |
| 4 | 18.4839 | 1.84 × 10−4 | 18.4835 | 2.90 × 10−4 | 18.4839 | 4.84 × 10−4 | 18.4833 | 1.86 × 10−4 | 18.4813 | 2.30 × 10−3 | 18.4839 | 3.16 × 10−2 | |
| 5 | 21.3181 | 1.64 × 10−4 | 21.3179 | 2.35 × 10−3 | 21.318 | 2.65 × 10−3 | 21.3178 | 1.02 × 10−3 | 21.3125 | 1.27 × 10−2 | 21.3156 | 6.00 × 10−3 | |
| 3 | 2 | 12.6999 | 1.84 × 10−9 | 12.6999 | 1.84 × 10−9 | 12.6999 | 1.84 × 10−9 | 12.6999 | 1.84 × 10−9 | 12.6999 | 1.84 × 10−9 | 12.6999 | 5.73 × 10−5 |
| 3 | 15.8406 | 4.84 × 10−5 | 15.8377 | 1.00 × 10−3 | 15.8406 | 7.36 × 10−4 | 15.8406 | 1.18 × 10−3 | 15.8377 | 2.55 × 10−3 | 15.8406 | 1.00 × 10−3 | |
| 4 | 18.9081 | 4.91 × 10−5 | 18.9079 | 6.67 × 10−4 | 18.9081 | 0 | 18.9081 | 4.89 × 10−5 | 18.908 | 2.96 × 10−3 | 18.9081 | 3.40 × 10−3 | |
| 5 | 21.6937 | 2.00 × 10−5 | 21.609 | 2.98 × 10−2 | 21.6934 | 3.81 × 10−5 | 21.6937 | 7.03 × 10−4 | 21.6935 | 1.19 × 10−3 | 21.6937 | 2.49 × 10−3 | |
| 4 | 2 | 12.458 | 3.68 × 10−9 | 12.458 | 3.68 × 10−9 | 12.458 | 4.04 × 10−5 | 12.458 | 3.68 × 10−9 | 12.458 | 2.12 × 10−5 | 12.458 | 1.21 × 10−3 |
| 3 | 15.5803 | 3.68 × 10−9 | 15.5803 | 3.68 × 10−9 | 15.5803 | 3.05 × 10−5 | 15.5803 | 3.68 × 10−9 | 15.5803 | 3.06 × 10−3 | 15.5803 | 3.07 × 10−4 | |
| 4 | 18.4835 | 9.69 × 10−4 | 18.4834 | 1.39 × 10−3 | 18.4834 | 1.56 × 10−3 | 18.4834 | 8.01 × 10−5 | 18.4806 | 1.26 × 10−3 | 18.4814 | 7.04 × 10−4 | |
| 5 | 21.2255 | 5.82 × 10−3 | 21.2089 | 8.52 × 10−3 | 21.2211 | 5.99 × 10−3 | 21.2254 | 6.81 × 10−3 | 21.2155 | 1.02 × 10−2 | 21.2211 | 6.13 × 10−3 | |
| 5 | 2 | 12.2672 | 1.84 × 10−9 | 12.2672 | 1.84 × 10−9 | 12.2672 | 1.84 × 10−9 | 12.2672 | 1.84 × 10−9 | 12.2672 | 1.84 × 10−9 | 12.2665 | 1.84 × 10−9 |
| 3 | 15.2393 | 1.12 × 10−3 | 15.2023 | 1.93 × 10−2 | 15.1498 | 1.67 × 10−2 | 15.2393 | 1.30 × 10−2 | 15.2393 | 1.30 × 10−2 | 15.2383 | 1.32 × 10−3 | |
| 4 | 18.0758 | 1.63 × 10−2 | 18.0758 | 2.38 × 10−2 | 18.0756 | 1.24 × 10−4 | 18.0758 | 1.47 × 10−2 | 18.0757 | 3.41 × 10−2 | 18.0754 | 5.10 × 10−3 | |
| 5 | 20.7597 | 1.78 × 10−2 | 20.6966 | 4.23 × 10−2 | 20.7506 | 2.79 × 10−2 | 20.6622 | 3.78 × 10−2 | 20.7588 | 3.35 × 10−2 | 20.6768 | 3.75 × 10−2 | |
| 6 | 2 | 12.6459 | 3.68 × 10−9 | 12.6459 | 3.68 × 10−9 | 12.6459 | 3.68 × 10−9 | 12.6459 | 3.68 × 10−9 | 12.6459 | 5.35 × 10−6 | 12.6459 | 3.16 × 10−5 |
| 3 | 15.8348 | 3.68 × 10−9 | 15.8348 | 3.68 × 10−9 | 15.8348 | 3.68 × 10−9 | 15.8348 | 3.68 × 10−9 | 15.8348 | 5.86 × 10−5 | 15.8346 | 7.96 × 10−4 | |
| 4 | 18.8099 | 6.43 × 10−6 | 18.8099 | 6.43 × 10−6 | 18.8099 | 4.23 × 10−5 | 18.8099 | 3.03 × 10−5 | 18.8089 | 5.43 × 10−4 | 18.8099 | 1.48 × 10−3 | |
| 5 | 21.5849 | 7.36 × 10−5 | 21.5849 | 1.47 × 10−4 | 21.5817 | 8.43 × 10−3 | 21.5849 | 7.23 × 10−5 | 21.5556 | 1.26 × 10−2 | 21.5849 | 1.02 × 10−2 | |
| 7 | 2 | 12.4226 | 3.68 × 10−9 | 12.4226 | 3.68 × 10−9 | 12.4226 | 3.68 × 10−9 | 12.4226 | 3.68 × 10−9 | 12.4226 | 3.68 × 10−9 | 12.4226 | 3.98 × 10−5 |
| 3 | 15.4792 | 5.52 × 10−9 | 15.4792 | 5.52 × 10−9 | 15.4792 | 5.52 × 10−9 | 15.4792 | 5.52 × 10−9 | 15.4792 | 5.37 × 10−5 | 15.4792 | 4.44 × 10−5 | |
| 4 | 18.3182 | 2.12 × 10−5 | 18.3181 | 2.41 × 10−2 | 18.3182 | 6.18 × 10−5 | 18.3181 | 2.84 × 10−5 | 18.3181 | 4.27 × 10−3 | 18.3182 | 3.07 × 10−3 | |
| 5 | 21.0502 | 7.07 × 10−5 | 20.9663 | 3.46 × 10−2 | 20.9277 | 6.17 × 10−4 | 21.0501 | 2.16 × 10−2 | 21.0492 | 2.60 × 10−2 | 21.0502 | 3.01 × 10−2 | |
| 8 | 2 | 12.0856 | 1.33 × 10−4 | 12.0853 | 2.78 × 10−3 | 12.0853 | 1.75 × 10−3 | 12.0853 | 1.33 × 10−5 | 12.0853 | 1.77 × 10−3 | 12.0853 | 8.05 × 10−4 |
| 3 | 15.3334 | 5.52 × 10−9 | 15.1937 | 3.60 × 10−2 | 15.3334 | 5.52 × 10−9 | 15.3334 | 5.52 × 10−9 | 15.3334 | 9.91 × 10−4 | 15.3334 | 4.08 × 10−4 | |
| 4 | 18.2572 | 7.30 × 10−4 | 18.256 | 5.24 × 10−3 | 18.2552 | 1.02 × 10−3 | 18.2562 | 4.88 × 10−4 | 18.2573 | 2.32 × 10−3 | 18.2547 | 2.94 × 10−3 | |
| 5 | 21.0181 | 1.25 × 10−3 | 21.0155 | 3.78 × 10−2 | 21.0173 | 1.49 × 10−3 | 21.0142 | 3.70 × 10−2 | 21.0163 | 1.57 × 10−2 | 21.0136 | 2.38 × 10−3 | |
| Image | K | DHHO/M | HHO | TLBO | WOA-TH | IDSA | BDE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | MSE | PSNR | MSE | PSNR | MSE | PSNR | MSE | PSNR | MSE | PSNR | MSE | ||
| 1 | 2 | 13.4568 | 3409.6288 | 13.5059 | 3409.6288 | 13.4568 | 3409.6288 | 13.4568 | 3409.6288 | 13.4568 | 3409.6288 | 13.4568 | 3409.6288 |
| 3 | 20.8043 | 541.7281 | 18.7437 | 541.7281 | 18.7437 | 1101.2048 | 18.7437 | 1079.8563 | 18.8912 | 1101.2048 | 18.8668 | 1101.2048 | |
| 4 | 23.5379 | 286.5668 | 23.5379 | 288.2504 | 23.5379 | 288.2504 | 23.5379 | 288.2504 | 23.4893 | 286.8563 | 23.4844 | 288.2504 | |
| 5 | 25.3432 | 190.0378 | 25.2873 | 190.4263 | 25.3432 | 190.0378 | 25.2458 | 190.0378 | 25.3091 | 199.5299 | 24.8902 | 192.3651 | |
| 2 | 2 | 13.761 | 2793.6353 | 13.761 | 2793.6353 | 13.761 | 2793.6353 | 13.761 | 2793.6353 | 13.761 | 2793.6353 | 13.761 | 2793.6353 |
| 3 | 17.1656 | 1274.8825 | 17.1656 | 1274.8825 | 17.1656 | 1274.8825 | 17.1656 | 1274.8825 | 17.1656 | 1274.8825 | 17.1656 | 1274.8825 | |
| 4 | 19.8508 | 690.9693 | 19.6349 | 725.6155 | 19.8508 | 690.9693 | 19.5626 | 738.4191 | 20.126 | 638.7005 | 19.8508 | 690.9693 | |
| 5 | 22.2059 | 393.4485 | 21.9532 | 415.6597 | 21.962 | 414.8152 | 21.8581 | 424.2548 | 22.073 | 403.525 | 21.8664 | 423.4967 | |
| 3 | 2 | 14.6099 | 2250.563 | 14.6099 | 2250.563 | 14.6099 | 2250.563 | 14.6099 | 2250.563 | 14.6099 | 2250.563 | 14.6099 | 2250.563 |
| 3 | 17.7343 | 1096.4772 | 17.0737 | 1316.3943 | 17.0737 | 1316.3943 | 17.0737 | 1316.3943 | 17.7343 | 1096.4772 | 17.0737 | 1316.3943 | |
| 4 | 19.5277 | 729.8596 | 19.4491 | 743.2218 | 19.4491 | 743.2218 | 19.4491 | 743.2218 | 19.4482 | 743.4005 | 19.4491 | 743.2218 | |
| 5 | 24.4587 | 238.8742 | 22.7205 | 395.9433 | 22.6857 | 401.4084 | 22.6857 | 401.4084 | 22.6956 | 401.0393 | 22.6857 | 401.4084 | |
| 4 | 2 | 14.1596 | 2518.0049 | 14.1596 | 2518.0049 | 14.1596 | 2518.0049 | 14.1596 | 2518.0049 | 14.1596 | 2518.0049 | 14.1596 | 2518.0049 |
| 3 | 17.3051 | 1316.1756 | 17.3051 | 1316.1756 | 17.3051 | 1316.1756 | 17.3051 | 1316.1756 | 17.3486 | 1308.8014 | 17.3051 | 1316.1756 | |
| 4 | 20.3568 | 652.8288 | 20.3524 | 653.8501 | 20.3524 | 653.8501 | 20.2761 | 672.0299 | 19.4048 | 764.8489 | 20.3524 | 653.8501 | |
| 5 | 24.0586 | 266.308 | 22.6141 | 375.5379 | 22.8347 | 354.1505 | 22.5577 | 379.7771 | 22.9103 | 356.3137 | 22.3481 | 392.8026 | |
| 5 | 2 | 12.3149 | 3817.5316 | 12.3149 | 3817.5316 | 12.3149 | 3817.5316 | 12.3149 | 3817.5316 | 12.3149 | 3817.5316 | 12.3247 | 3809.1362 |
| 3 | 14.3753 | 2377.2328 | 13.9334 | 2642.1422 | 14.3388 | 2396.5364 | 14.3753 | 2377.2328 | 14.3753 | 2377.2328 | 14.3747 | 2377.5557 | |
| 4 | 16.904 | 1355.9069 | 16.8586 | 1368.8135 | 16.7536 | 1413.0432 | 16.8586 | 1368.8135 | 16.8158 | 1381.3574 | 16.8516 | 1370.5727 | |
| 5 | 18.529 | 941.6725 | 17.4932 | 1166.1194 | 17.6121 | 1131.203 | 17.661 | 1117.2575 | 17.5692 | 1142.5529 | 17.4611 | 1174.9531 | |
| 6 | 2 | 15.4096 | 1875.6465 | 15.4096 | 1875.6465 | 15.4096 | 1875.6465 | 15.4096 | 1875.6465 | 15.4096 | 1875.6465 | 15.4096 | 1875.6465 |
| 3 | 17.3586 | 1204.8869 | 17.3586 | 1204.8869 | 17.3586 | 1204.8869 | 17.3586 | 1204.8869 | 17.3576 | 1205.2089 | 17.3217 | 1213.4404 | |
| 4 | 18.6145 | 906.6325 | 18.6145 | 906.6325 | 18.6145 | 906.6325 | 18.6145 | 906.6325 | 18.5634 | 916.8623 | 18.6145 | 906.6325 | |
| 5 | 20.6141 | 586.8374 | 20.6141 | 586.8374 | 20.4926 | 603.118 | 20.6141 | 586.8374 | 20.1165 | 651.1384 | 20.6141 | 586.8374 | |
| 7 | 2 | 12.9658 | 3316.6781 | 12.9658 | 3316.6781 | 12.9658 | 3316.6781 | 12.9658 | 3316.6781 | 12.9658 | 3316.6781 | 12.9658 | 3316.6781 |
| 3 | 16.2594 | 1542.3302 | 16.2594 | 1542.3302 | 16.2594 | 1542.3302 | 16.2594 | 1542.3302 | 16.2594 | 1542.3302 | 16.2594 | 1542.3302 | |
| 4 | 19.9285 | 710.127 | 19.8763 | 720.2965 | 19.9285 | 710.127 | 19.8208 | 732.3273 | 19.8763 | 720.2965 | 19.9285 | 710.127 | |
| 5 | 22.7765 | 353.4079 | 21.725 | 476.8748 | 22.5737 | 406.4345 | 21.5981 | 484.4584 | 21.6863 | 481.3556 | 21.725 | 476.8748 | |
| 8 | 2 | 14.2476 | 2953.5281 | 14.2452 | 2956.1504 | 14.2452 | 2956.1504 | 14.2452 | 2956.1504 | 14.2452 | 2956.1504 | 14.2452 | 2956.1504 |
| 3 | 18.4536 | 854.9528 | 16.9544 | 1753.3657 | 16.9544 | 1753.3657 | 16.9544 | 1753.3657 | 16.9544 | 1753.3657 | 16.9544 | 1753.3657 | |
| 4 | 24.6745 | 222.5721 | 24.5916 | 227.417 | 24.5902 | 227.4794 | 24.5902 | 227.4794 | 20.7867 | 1039.7204 | 20.8096 | 1035.361 | |
| 5 | 25.5344 | 183.0689 | 25.2902 | 193.2529 | 25.0615 | 204.0797 | 25.1686 | 199.832 | 25.2937 | 193.1147 | 25.1855 | 198.1814 | |
| Image | K | DHHO/M | HHO | TLBO | WOA-TH | IDSA | BDE | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SSIM | FSIM | SSIM | FSIM | SSIM | FSIM | SSIM | FSIM | SSIM | FSIM | SSIM | FSIM | ||
| 1 | 2 | 0.3288 | 0.5472 | 0.3319 | 0.549 | 0.3288 | 0.5472 | 0.3288 | 0.5472 | 0.3288 | 0.5472 | 0.3288 | 0.5472 |
| 3 | 0.5893 | 0.7387 | 0.57 | 0.7148 | 0.57 | 0.7148 | 0.57 | 0.7148 | 0.577 | 0.7203 | 0.5776 | 0.7205 | |
| 4 | 0.7415 | 0.827 | 0.7415 | 0.827 | 0.7415 | 0.827 | 0.7415 | 0.827 | 0.7415 | 0.8269 | 0.7407 | 0.8261 | |
| 5 | 0.7945 | 0.8763 | 0.7945 | 0.8761 | 0.7945 | 0.8761 | 0.7917 | 0.8738 | 0.794 | 0.8755 | 0.7838 | 0.866 | |
| 2 | 2 | 0.2696 | 0.5527 | 0.2696 | 0.5527 | 0.2696 | 0.5527 | 0.2696 | 0.5527 | 0.2696 | 0.5527 | 0.2696 | 0.5527 |
| 3 | 0.4376 | 0.6476 | 0.4376 | 0.6476 | 0.4376 | 0.6476 | 0.4376 | 0.6476 | 0.4376 | 0.6476 | 0.4376 | 0.6476 | |
| 4 | 0.5737 | 0.7436 | 0.5634 | 0.7323 | 0.5737 | 0.7382 | 0.56 | 0.73 | 0.5829 | 0.7382 | 0.5737 | 0.7382 | |
| 5 | 0.6669 | 0.7981 | 0.6577 | 0.7928 | 0.6584 | 0.7936 | 0.6536 | 0.79 | 0.663 | 0.7965 | 0.6543 | 0.7902 | |
| 3 | 2 | 0.3643 | 0.6627 | 0.3643 | 0.6627 | 0.3643 | 0.6627 | 0.3643 | 0.6627 | 0.3643 | 0.6627 | 0.3643 | 0.6627 |
| 3 | 0.4218 | 0.7239 | 0.4209 | 0.7217 | 0.4218 | 0.7217 | 0.4218 | 0.7217 | 0.4209 | 0.7239 | 0.4218 | 0.7217 | |
| 4 | 0.4886 | 0.7808 | 0.4863 | 0.7801 | 0.4863 | 0.7801 | 0.4863 | 0.7801 | 0.4864 | 0.78 | 0.4863 | 0.7801 | |
| 5 | 0.6693 | 0.8431 | 0.5795 | 0.837 | 0.5785 | 0.837 | 0.5785 | 0.837 | 0.5788 | 0.837 | 0.5785 | 0.837 | |
| 4 | 2 | 0.4043 | 0.6463 | 0.4043 | 0.6463 | 0.4043 | 0.6463 | 0.4043 | 0.6463 | 0.4043 | 0.6463 | 0.4043 | 0.6463 |
| 3 | 0.5746 | 0.7584 | 0.5734 | 0.758 | 0.5734 | 0.758 | 0.5734 | 0.758 | 0.5734 | 0.758 | 0.5734 | 0.758 | |
| 4 | 0.7328 | 0.8331 | 0.7323 | 0.8331 | 0.7323 | 0.8331 | 0.7291 | 0.832 | 0.698 | 0.813 | 0.7323 | 0.8336 | |
| 5 | 0.8336 | 0.8869 | 0.792 | 0.8683 | 0.7966 | 0.8692 | 0.7909 | 0.8678 | 0.7978 | 0.8711 | 0.7883 | 0.8655 | |
| 5 | 2 | 0.4806 | 0.6389 | 0.4806 | 0.6389 | 0.4806 | 0.6389 | 0.4806 | 0.6389 | 0.4806 | 0.6389 | 0.4802 | 0.6385 |
| 3 | 0.5432 | 0.67 | 0.619 | 0.6865 | 0.4693 | 0.6537 | 0.5432 | 0.67 | 0.5432 | 0.67 | 0.5435 | 0.67 | |
| 4 | 0.6459 | 0.7142 | 0.6454 | 0.7138 | 0.6398 | 0.7117 | 0.6454 | 0.7138 | 0.6459 | 0.7137 | 0.6456 | 0.714 | |
| 5 | 0.694 | 0.7515 | 0.679 | 0.7417 | 0.7136 | 0.7506 | 0.7093 | 0.7474 | 0.7109 | 0.7485 | 0.7132 | 0.7504 | |
| 6 | 2 | 0.4053 | 0.6628 | 0.4053 | 0.6628 | 0.4053 | 0.6628 | 0.4053 | 0.6628 | 0.4053 | 0.6628 | 0.4053 | 0.6628 |
| 3 | 0.4741 | 0.7409 | 0.4741 | 0.7409 | 0.4741 | 0.7409 | 0.4741 | 0.7409 | 0.474 | 0.7408 | 0.4717 | 0.74 | |
| 4 | 0.5283 | 0.7827 | 0.5283 | 0.7827 | 0.5283 | 0.7827 | 0.5283 | 0.7827 | 0.5259 | 0.7822 | 0.5283 | 0.7827 | |
| 5 | 0.5595 | 0.8096 | 0.5589 | 0.8092 | 0.5548 | 0.8075 | 0.5589 | 0.8092 | 0.5589 | 0.8092 | 0.5589 | 0.8092 | |
| 7 | 2 | 0.4061 | 0.6178 | 0.4061 | 0.6178 | 0.4061 | 0.6178 | 0.4061 | 0.6178 | 0.4061 | 0.6178 | 0.4061 | 0.6178 |
| 3 | 0.5456 | 0.7131 | 0.5456 | 0.7131 | 0.5456 | 0.7131 | 0.5456 | 0.7131 | 0.5456 | 0.7131 | 0.5456 | 0.7131 | |
| 4 | 0.6569 | 0.7859 | 0.6557 | 0.7858 | 0.6569 | 0.7859 | 0.654 | 0.7853 | 0.6557 | 0.7858 | 0.6569 | 0.7859 | |
| 5 | 0.7557 | 0.8372 | 0.7234 | 0.829 | 0.7434 | 0.8306 | 0.7194 | 0.8261 | 0.7219 | 0.8282 | 0.7234 | 0.829 | |
| 8 | 2 | 0.2264 | 0.4841 | 0.2261 | 0.484 | 0.2261 | 0.484 | 0.2261 | 0.484 | 0.2261 | 0.484 | 0.2261 | 0.484 |
| 3 | 0.5319 | 0.659 | 0.3864 | 0.6196 | 0.3864 | 0.6196 | 0.3864 | 0.6196 | 0.3864 | 0.6196 | 0.3864 | 0.6196 | |
| 4 | 0.6547 | 0.7485 | 0.6539 | 0.7473 | 0.6532 | 0.7458 | 0.6539 | 0.7473 | 0.5122 | 0.7049 | 0.5152 | 0.7099 | |
| 5 | 0.6961 | 0.7923 | 0.6829 | 0.777 | 0.6724 | 0.7666 | 0.6804 | 0.7752 | 0.6829 | 0.7771 | 0.6744 | 0.7686 | |
| Image | K | DHHO/M versus | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| HHO | TLBO | WOA-TH | IDSA | BDE | |||||||
| p | h | p | h | p | h | p | h | p | h | ||
| 1 | 2 | <0.05 | 1 | <0.05 | 1 | 0.4197 | 0 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.0957 | 0 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 2 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.0784 | 0 | |
| 4 | 0.0692 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 3 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | 0.2117 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 5 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.2624 | 0 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 6 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | 0.0544 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | 0.1342 | 0 | |
| 5 | 0.2744 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 7 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 3 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 8 | 2 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 |
| 3 | 0.0963 | 0 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 4 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| 5 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | <0.05 | 1 | |
| K | DHHO/M | HHO | TLBO | WOA-TH | IDSA | BDE |
|---|---|---|---|---|---|---|
| 2 | 3.10417 | 3.44792 | 3.53125 | 3.41667 | 3.63542 | 3.86458 |
| 3 | 2.39583 | 3.85417 | 3.83333 | 3.41667 | 3.60417 | 3.89583 |
| 4 | 1.93750 | 3.61458 | 3.36458 | 3.61458 | 4.67708 | 3.79167 |
| 5 | 1.29167 | 3.84375 | 3.37500 | 4.21875 | 3.80208 | 4.46875 |
| Overall | 2.18229 | 3.69010 | 3.52604 | 3.66667 | 3.92969 | 4.00521 |
| K | Chi-Square Value | p-Value |
|---|---|---|
| 2 | 20.1095890410959 | 1.19191051533946 × 10−3 |
| 3 | 40.6933911159263 | 1.08206724960841 × 10−7 |
| 4 | 65.6772334293948 | 8.10948996472364 × 10−13 |
| 5 | 95.8565989847716 | 3.94253504591917 × 10−19 |
| Overall | 194.274459078081 | 4.76396506070144 × 10−40 |
| K | DHHO/M | HHO | TLBO | WOA-TH | IDSA | BDE |
|---|---|---|---|---|---|---|
| 2 | 2.198133 | 2.212233 | 1.797438 | 1.844933 | 1.565033 | 2.057214 |
| 3 | 2.223321 | 2.229533 | 1.800174 | 1.852567 | 1.654733 | 2.151333 |
| 4 | 2.263767 | 2.339267 | 1.824733 | 1.896333 | 1.663767 | 2.314633 |
| 5 | 2.342478 | 2.390067 | 1.828633 | 1.927133 | 1.681547 | 2.323733 |
| Image | K | DHHO/M | HHO | TLBO | WOA-TH | IDSA | BDE |
|---|---|---|---|---|---|---|---|
| 1 | 10 | 34.2109 | 34.2098 | 34.2103 | 34.2107 | 34.1789 | 34.1621 |
| 15 | 43.9417 | 43.9326 | 43.9049 | 43.9337 | 43.6787 | 43.8603 | |
| 20 | 52.05 | 52.0305 | 51.4385 | 52.0499 | 51.6164 | 51.6291 | |
| 2 | 10 | 33.3497 | 33.3333 | 33.3479 | 33.3494 | 33.2628 | 33.333 |
| 15 | 42.8291 | 42.8093 | 42.7608 | 42.8261 | 42.6363 | 42.7508 | |
| 20 | 50.7191 | 50.5899 | 50.381 | 50.67 | 50.2388 | 50.3818 | |
| 3 | 10 | 33.8971 | 33.8945 | 33.8949 | 33.8953 | 33.8526 | 33.8872 |
| 15 | 43.7344 | 43.5907 | 43.5659 | 43.735 | 43.5409 | 43.6546 | |
| 20 | 51.8463 | 51.7497 | 51.2457 | 51.8042 | 51.5 | 51.443 | |
| 4 | 10 | 33.0248 | 33.0049 | 32.9986 | 33.006 | 32.8715 | 32.9839 |
| 15 | 42.5643 | 42.5557 | 42.5182 | 42.5495 | 42.1679 | 42.4222 | |
| 20 | 50.404 | 50.2911 | 49.8884 | 50.3453 | 49.9967 | 50.2819 | |
| 5 | 10 | 32.1816 | 32.1393 | 32.1204 | 32.1081 | 32.1083 | 32.0863 |
| 15 | 41.5955 | 41.5162 | 41.526 | 41.4936 | 41.2365 | 41.315 | |
| 20 | 49.3631 | 49.1688 | 48.5774 | 49.2279 | 48.3306 | 49.1217 | |
| 6 | 10 | 33.6055 | 33.5978 | 33.5762 | 33.5641 | 33.5589 | 33.5871 |
| 15 | 43.4567 | 43.3523 | 43.2951 | 43.4393 | 43.2992 | 43.4059 | |
| 20 | 51.706 | 51.6251 | 51.1347 | 51.6806 | 51.2283 | 51.4454 | |
| 7 | 10 | 32.8232 | 32.8055 | 32.825 | 32.8192 | 32.6911 | 32.6068 |
| 15 | 42.3475 | 42.3111 | 42.2273 | 42.2965 | 41.9677 | 42.3149 | |
| 20 | 50.3583 | 50.2802 | 49.6741 | 50.331 | 49.5638 | 50.1 | |
| 8 | 10 | 32.8858 | 32.813 | 32.8833 | 32.8505 | 32.8148 | 32.825 |
| 15 | 42.3784 | 42.2574 | 42.3384 | 42.3509 | 41.9624 | 42.2916 | |
| 20 | 50.3095 | 50.2246 | 50.093 | 50.2379 | 49.9046 | 50.0384 |
| Image | K | Objective Value | PSNR | ||||
| DHHO/M | MGOA | MABC | DHHO/M | MGOA | MABC | ||
| 1 | 10 | 3.6662 | 3.6649 | 3.6662 | 30.5093 | 27.7705 | 31.1043 |
| 15 | 5.3316 | 5.3109 | 5.3302 | 34.2626 | 28.6303 | 33.4524 | |
| 20 | 6.995 | 6.948 | 6.9866 | 36.8371 | 33.8588 | 34.1846 | |
| 3 | 10 | 3.6661 | 3.665 | 3.6661 | 25.7383 | 24.9989 | 26.0445 |
| 15 | 5.3313 | 5.3141 | 5.3299 | 33.3645 | 28.9334 | 30.1357 | |
| 20 | 6.9947 | 6.9516 | 6.9863 | 35.3185 | 32.9205 | 33.9627 | |
| 5 | 10 | 3.6654 | 3.6571 | 3.6654 | 22.0935 | 20.8869 | 21.9164 |
| 15 | 5.3288 | 5.3084 | 5.3262 | 25.5957 | 27.7061 | 27.5186 | |
| 20 | 6.9896 | 6.837 | 6.9741 | 34.1475 | 33.0881 | 28.4798 | |
| 7 | 10 | 3.6659 | 3.6643 | 3.6658 | 28.0284 | 26.1506 | 27.273 |
| 15 | 5.3305 | 5.318 | 5.3287 | 33.5291 | 29.8082 | 27.8041 | |
| 20 | 6.9924 | 6.9311 | 6.9836 | 36.8653 | 32.2124 | 34.0468 | |
| Image | K | SSIM | FSIM | ||||
| DHHO/M | MGOA | MABC | DHHO/M | MGOA | MABC | ||
| 1 | 10 | 0.9157 | 0.8811 | 0.9225 | 0.9579 | 0.9236 | 0.9622 |
| 15 | 0.9579 | 0.8956 | 0.9495 | 0.9806 | 0.9351 | 0.9762 | |
| 20 | 0.9756 | 0.9541 | 0.9638 | 0.9886 | 0.9772 | 0.9773 | |
| 3 | 10 | 0.6904 | 0.6883 | 0.6967 | 0.9156 | 0.8771 | 0.9157 |
| 15 | 0.8827 | 0.8322 | 0.8095 | 0.9636 | 0.9241 | 0.9442 | |
| 20 | 0.9251 | 0.9018 | 0.8911 | 0.976 | 0.9557 | 0.9633 | |
| 5 | 10 | 0.816 | 0.7854 | 0.8113 | 0.8522 | 0.8217 | 0.8501 |
| 15 | 0.8844 | 0.8506 | 0.8368 | 0.8888 | 0.8844 | 0.9139 | |
| 20 | 0.9224 | 0.9107 | 0.9077 | 0.9578 | 0.9344 | 0.9298 | |
| 7 | 10 | 0.9001 | 0.8294 | 0.8861 | 0.9376 | 0.8823 | 0.9324 |
| 15 | 0.952 | 0.9127 | 0.8916 | 0.9725 | 0.939 | 0.9371 | |
| 20 | 0.9749 | 0.9468 | 0.9555 | 0.9842 | 0.9549 | 0.9733 | |
| Image | K | Objective Value | PSNR | ||||
| DHHO/M | MFPA | GWO | DHHO/M | MFPA | GWO | ||
| 2 | 10 | 1364.9884 | 1349.264 | 1363.1902 | 27.4462 | 30.0066 | 27.6228 |
| 15 | 1376.5148 | 1365.331 | 1375.1601 | 32.3029 | 33.6342 | 32.4534 | |
| 20 | 1381.0397 | 1373.8639 | 1379.5538 | 36.5965 | 35.5419 | 36.5278 | |
| 4 | 10 | 1304.5892 | 1289.3595 | 1304.3497 | 29.0959 | 29.2216 | 29.4061 |
| 15 | 1315.0389 | 1302.8059 | 1314.4674 | 33.3247 | 31.413 | 34.5001 | |
| 20 | 1319.0692 | 1311.4133 | 1317.3414 | 36.1074 | 36.618 | 36.1379 | |
| 6 | 10 | 5027.6737 | 5013.6505 | 5025.5149 | 26.5928 | 23.5726 | 25.7915 |
| 15 | 5043.2255 | 5034.3596 | 5041.6036 | 32.9168 | 27.9594 | 29.957 | |
| 20 | 5049.6773 | 5040.9838 | 5047.5628 | 35.0998 | 33.317 | 33.8307 | |
| 8 | 10 | 934.5128 | 925.9764 | 934.3473 | 31.6049 | 31.1744 | 30.8108 |
| 15 | 943.6876 | 934.3932 | 942.2697 | 35.8537 | 32.9725 | 35.0404 | |
| 20 | 947.3744 | 941.3551 | 945.2916 | 37.3744 | 37.2122 | 37.3125 | |
| Image | K | SSIM | FSIM | ||||
| DHHO/M | MFPA | GWO | DHHO/M | MFPA | GWO | ||
| 2 | 10 | 0.9218 | 0.8962 | 0.9106 | 0.9395 | 0.9352 | 0.9337 |
| 15 | 0.9651 | 0.9459 | 0.9577 | 0.9746 | 0.9702 | 0.9688 | |
| 20 | 0.9796 | 0.9686 | 0.9779 | 0.987 | 0.9824 | 0.9829 | |
| 4 | 10 | 0.9532 | 0.9343 | 0.9487 | 0.9561 | 0.9525 | 0.9533 |
| 15 | 0.9854 | 0.954 | 0.9796 | 0.9853 | 0.968 | 0.979 | |
| 20 | 0.99 | 0.985 | 0.9892 | 0.9899 | 0.989 | 0.988 | |
| 6 | 10 | 0.8141 | 0.7369 | 0.7833 | 0.9151 | 0.8877 | 0.9125 |
| 15 | 0.9405 | 0.8123 | 0.8654 | 0.9496 | 0.9328 | 0.9619 | |
| 20 | 0.9633 | 0.9028 | 0.9269 | 0.9752 | 0.9658 | 0.9723 | |
| 8 | 10 | 0.9271 | 0.9029 | 0.9155 | 0.9571 | 0.9433 | 0.9474 |
| 15 | 0.9655 | 0.9314 | 0.9611 | 0.979 | 0.9579 | 0.9798 | |
| 20 | 0.9764 | 0.9625 | 0.9745 | 0.9876 | 0.9799 | 0.9856 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, H.; Lang, C.; Oliva, D.; Song, W.; Peng, X. Dynamic Harris Hawks Optimization with Mutation Mechanism for Satellite Image Segmentation. Remote Sens. 2019, 11, 1421. https://doi.org/10.3390/rs11121421
Jia H, Lang C, Oliva D, Song W, Peng X. Dynamic Harris Hawks Optimization with Mutation Mechanism for Satellite Image Segmentation. Remote Sensing. 2019; 11(12):1421. https://doi.org/10.3390/rs11121421
Chicago/Turabian StyleJia, Heming, Chunbo Lang, Diego Oliva, Wenlong Song, and Xiaoxu Peng. 2019. "Dynamic Harris Hawks Optimization with Mutation Mechanism for Satellite Image Segmentation" Remote Sensing 11, no. 12: 1421. https://doi.org/10.3390/rs11121421
APA StyleJia, H., Lang, C., Oliva, D., Song, W., & Peng, X. (2019). Dynamic Harris Hawks Optimization with Mutation Mechanism for Satellite Image Segmentation. Remote Sensing, 11(12), 1421. https://doi.org/10.3390/rs11121421