An Optimal Decision-Tree Design Strategy and Its Application to Sea Ice Classification from SAR Imagery

Abstract

We introduce the fully automatic design of a numerically optimized decision-tree algorithm and demonstrate its application to sea ice classification from SAR data. In the decision tree, an initial multi-class classification problem is split up into a sequence of binary problems. Each branch of the tree separates one single class from all other remaining classes, using a class-specific selected feature set. We optimize the order of classification steps and the feature sets by combining classification accuracy and sequential search algorithms, looping over all remaining features in each branch. The proposed strategy can be adapted to different types of classifiers and measures for the class separability. In this study, we use a Bayesian classifier with non-parametric kernel density estimation of the probability density functions. We test our algorithm on simulated data as well as airborne and spaceborne SAR data over sea ice. For the simulated cases, average per-class classification accuracy is improved between 0.5% and 4% compared to traditional all-at-once classification. Classification accuracy for the airborne and spaceborne SAR datasets was improved by 2.5% and 1%, respectively. In all cases, individual classes can show larger improvements up to 8%. Furthermore, the selection of individual feature sets for each single class can provide additional insights into physical interpretation of different features. The improvement in classification results comes at the cost of longer computation time, in particular during the design and training stage. The final choice of the optimal algorithm therefore depends on time constraints and application purpose.

1. Introduction

The focus of this study is the development of a strategy for automatic optimization of a decision tree for classification problems. While the proposed algorithm is generic and can be applied to any given classification problem, we demonstrate its potential on the example of sea ice type classification in Synthetic Aperture Radar (SAR) data.

There is a strong interest in ice type classification in particular from an operational perspective. As, in particular, the summer sea ice extent declines [1,2,3], the Arctic Ocean becomes more accessible to marine traffic and offshore operations [4], to which sea ice and icebergs can pose a significant danger [5,6,7]. Fast, robust and reliable methods for mapping of sea ice types are therefore needed to ensure the safety of shipping and offshore operations in the Arctic.

There are several ice services worldwide that produce sea ice charts on a regular daily basis. Usually, the charts show total ice concentration or a combination of ice concentration and ice type. Because of its independence of daylight and weather conditions, SAR provides an excellent tool for year-round sea ice observations. It is therefore one of the main data sources for mapping of ice types and ice chart production. For now, however, analysis of the images is mostly performed manually. With new satellite missions being launched and an increasing number of images available, this manual approach needs to be supplemented by reliable methods for automatic or semi-automatic mapping of sea ice conditions.

There are already a substantial number of studies that investigate automatic or semi-automatic sea ice classification using SAR imagery. Many approaches use traditional classification strategies, that separate all classes in one step and assign a class label to each pixel. Common algorithms are Bayesian classifiers [8,9], support vector machines [10,11] or neural networks [12,13,14,15,16]. All of these methods require training data with known class labels in order to determine the decision boundaries between classes. In segmentation-based approaches, on the other hand, no training data is needed. The image is simply segmented into regions [17,18] with statistically similar backscatter. However, the actual class labels, i.e., the ice type of each segment, are initially unknown and have to be determined after the segmentation [19,20].

Both classification and segmentation methods need a set of features that allows to distinguish between different surface types. There are numerous studies investigating the potential of various features for ice type classification. Commonly used features are simple backscatter intensities [21], texture features [22,23,24] or polarimetric features [9,25]. The performance of features for separation of ice types can furthermore differ depending on the ice situation (winter or melt season) and the wavelength of the radar system [26,27,28]. Prior to classification or segmentation, a set of suitable features needs to be generated. There are various established methods to do so, including feature transformations such as Principal Component Analysis (PCA) or feature selection methods such as Sequential Forward/Backward Feature Selection (SFFS, SBFS) [29]. In the methods described so far, one common feature set is selected for the entire classification or segmentation problem. This constitutes the main conceptual difference compared to decision trees.

Decision trees (DT) are a particular type of supervised forward classifier that requires training data with known class labels. In contrast to the classification methods mentioned earlier, where all classes are separated in one step (all-at-once), a DT splits the multi-class decision into a series of binary decisions. It uses these binary splits to extract patterns or rules in a dataset [30]. DTs have been used for sea ice classification in various studies. For example, the authors of [31] employ a DT for discrimination of sea ice types and open water from dual co-polarized SAR, while the authors of [32] use it to classify multi-sensor satellite observations of a polynya region in the Ross Sea. In both of these studies, as in many other cases, the DTs are designed manually, based on local knowledge or manual interpretation of data. Automated trees, on the other hand, can be designed by applying splitting criteria and stop-splitting rules. However, single trees tend to show large variance, and in practice it is not uncommon for a small change in training data to result in a very different tree [29]. Random-forest (RF) classifiers are one established way to overcome this overfitting issue. As implied by the name, an RF classifier uses a large number of individual trees, each of which is designed from a randomly selected subset of the entire training set (Bootstrap Aggregation, Bagging) and a randomly selected subset of features. Each tree gives an individual class label as output and the final class is decided by a majority vote from all trees in the forest. Generalization of the method is achieved through the randomization of the different training subsets and thus overfitting to the training data is avoided. Single DTs as well as RFs are used by, e.g., Refs. [30,33] for monitoring of landfast ice and retrieval of melt ponds on multi-year ice, respectively.

The objective of our study is to develop the automatic design of a numerically optimized DT with regard to classification accuracy (CA). In contrast to the RF, our algorithm designs and uses only one single tree. Each branch of this tree classifies one single class and takes it out of the dataset. The order of classification steps and the chosen feature sets are selected by combining CA and sequential search algorithms. Depending on the available features and the balancing of the training data, we expect this optimized DT classifier to perform better than a traditional classifier. While the RF achieves generalization through random selection of training and feature subsets and a subsequent majority vote of a large number of independent trees, our algorithm generalizes through cross-validation over the entire training set during the design stage. The algorithm specifically tailors the feature set in each branch of the tree to the class that will be separated in that respective branch. Besides improved CA, these individually selected feature sets can also provide information on dominant scattering mechanisms for different ice types and on the potential of different features to distinguish between certain classes. This information is more difficult to obtain from an RF, which uses the majority vote of a large number of different trees with random feature sets.

We test our proposed method on a variety of simulated and real data and compare the results with those from all-at-once (AAO) classifiers. The remainder of this article is structured as follows: The fully automatic design of the DT is described in detail in Section 2. In Section 3, we introduce the datasets used for testing the algorithm performance. Section 4 presents the optimized tree designs and all classification results, followed by discussion and conclusion in Section 5 and Section 6, respectively.

2. Method

2.1. DT Design Strategy

Separation of sea ice types is a typical multi-class problem. A traditional AAO classification algorithm uses one set F of input features (e.g., radar intensities at different frequencies, polarimetric or texture parameters) to separate all classes ${\omega }_i$ in a single step (Figure 1). In a DT, this multi-class decision is replaced by several binary decisions with distinct feature sets $F_i$ (Figure 2). Both approaches are supervised and require training data for each class.

In the DT example, sketched in Figure 2, the order of separating single classes is given. The DT architecture is usually determined manually, based on expert knowledge of regional ice conditions at the given point in time. Class ${\omega }_1$ is classified in branch $B_1$, class ${\omega }_2$ in branch $B_2$ and a final binary decision separates ${\omega }_3$ and ${\omega }_4$ in branch $B_3$. Furthermore, feature sets $F_i$ are given, which are different in each branch $B_i$. In the final branch, the two remaining classes are classified simultaneously. The architecture of the tree, i.e., the order of classes and the chosen feature sets, needs to be determined in some way. We refer to this as the DT design stage. After the design stage, the finished tree can be used for forward classification of new samples, i.e., images acquired at similar ice and temperature ranges.

In this work, we present an automated design strategy for an optimal DT in terms of CA. The basic concept of our proposed DT design stage is sketched in Figure 3. In every branch, we test each of the remaining classes as a single class against the combination of all other remaining classes and calculate the average per-class CA. To ensure that the CA is independent of the training data, we use 100-fold cross validation, i.e., we randomly split all training data over the two step-specific classes into 100 sub-groups. Looping over these sub-groups, each of them is once retained for determining the CA, while the remaining sub-groups serve as training data. The results from all sub-groups are averaged to obtain the final score for the current step. The highest scoring class is selected as the single class ${\omega }_j$ for the current branch $B_i$. All samples from this class are taken out of the training data before the next branch. Note that other class-separability criteria than average per-class CA may be used at this stage without altering the proposed strategy for the DT design. To obtain the best CA for every single-class test within each branch, we run a Sequential Forward Feature Selection (SFFS) to determine the optimal feature set. The procedure of the SFFS is as follows:

• Compute the CA for each of the features individually. Select the feature with the highest score.
• Compute the CA for all possible pairs of features that contain the winner from the previous step. Select the best two-feature combination.
• Continue sequentially to add remaining features to the previously selected set, always choosing the highest scoring combination.
• Stop if the CA of the currently best feature set is lower than the CA of the best feature set from the previous step, or when all available features are selected.
• Select the feature set from the step with the maximum CA as the optimal one.

During the DT design stage, sketched in Figure 3, SFFS is performed in total eight times: Four times in branch $B_1$, three times in branch $B_2$ and once in the final branch $B_3$. As mentioned in many textbooks, the SFFS is in fact a sub-optimal method of feature selection, as there is no guarantee that the optimal two-dimensional feature set originates from the optimal one-dimensional one (or similar at higher levels). However, if many features are available, forming all possible combinations quickly results in a very large number of feature sets to test, which is impractical [29]. Nevertheless, the choice of feature selection can be adjusted depending on the available time and computational power. As long as a logical selection criterion is applied that results in an optimal choice of features in terms of this metric, the exact selection process does not alter the concept of the optimized DT design that we propose here.

2.2. Choice of Classifier

The concept of the DT design strategy can generally be applied to any classification algorithm. In this study, we use an algorithm based on Bayesian decision theory, which assigns the feature vector $\underline{x}$ for each pixel in the image to the most probable class ${\omega }_i$:

$$\underline{x}\to {\omega }_i\mathrm{if}P\left({\omega }_i\right|\underline{x})>P\left({\omega }_k\right|\underline{x})\forall k\ne i,$$

(1)

where $P\left({\omega }_i\right|\underline{x})$ is the posterior probability of class ${\omega }_i$, given pixel $\underline{x}$. Employing Bayes rule, the decision rule can be expressed through the likelihood ratio:

$$\underline{x}\to {\omega }_i\mathrm{if}\frac{p\left(\underline{x}\right|{\omega }_i)}{p\left(\underline{x}\right|{\omega }_k)}>\frac{P\left({\omega }_k\right)}{P\left({\omega }_i\right)}\forall k\ne i,$$

(2)

with the prior probabilities $P\left({\omega }_i\right)$ and the class-specific probability density functions (PDF) $p\left(\underline{x}\right|{\omega }_i)$. The prior probabilities reflect total abundances of different classes and can be estimated from training data or set equal for Maximum-Likelihood (ML) classification. The decision then depends entirely on the class-specific probability density functions (PDFs) $p\left(\underline{x}\right|{\omega }_i)$, which must be estimated from the data. For known parametric forms of class distributions, the parameters for each class can be estimated from the training data. If the form of the PDFs is unknown, it can be approximated through kernel density estimation (also known as Parzen windows [34]). Since we do not want to include assumptions about the PDFs in our algorithm, we have implemented Parzen windows with a multi-variate Gaussian kernel function to approximate the PDFs directly from the training data. The width of the Gaussian kernel function is estimated using Silverman’s rule of thumb [35] and the number of used kernels is controlled by the number of available training points.

2.3. Balancing of Probabilities

At various steps during the DT design stage, several single classes are combined to one mixed class ${\omega }_{mix}$. Each of these combinations requires a choice for the balancing of the prior probabilities, with the two basic options being an ML decision for the final result or an ML decision in every single branch. We choose to balance the prior probabilities for ML of the final result. Without prior knowledge about the data, this is the most natural approach to take. Furthermore, it corresponds to the balancing of an ML AAO classifier, and we score our results accordingly.

In practice, prior influence of single individual classes is removed when estimating class-specific PDFs and choosing equal prior probabilities. (Remember that the PDF by definition integrates to one). The prior probability $P\left({\omega }_{mix}\right)$ for a mixed class consisting of N individual classes must therefore be weighted by the factor N. The PDF $p\left(\underline{x}\right|{\omega }_{mix})$ of the mixed class can either be estimated by summing up and scaling the PDFs from the individual classes, or by a single kernel density estimation using all training samples from the combined classes. For the latter option, however, the number of training samples per class will be embedded in the resulting PDF and thus influence the balance of individual classes. We therefore compute the mixed PDF by summing up and scaling individual PDFs:

$$p\left(\underline{x}\right|{\omega }_{mix})=\frac{1}{N}·\sum _{i=1}^{N}p\left(\underline{x}\right|{\omega }_i)$$

(3)

The decision rule is now given by:

$$\underline{x}\to {\omega }_{single}\mathrm{if}\frac{p\left(\underline{x}\right|{\omega }_{single})}{p\left(\underline{x}\right|{\omega }_{mix})}>\frac{P\left({\omega }_{mix}\right)}{P\left({\omega }_{single}\right)}$$

(4)

With prior probabilities according to:

$$P\left({\omega }_{mix}\right)=\frac{N}{N+1}\mathrm{and}P\left({\omega }_{single}\right)=\frac{1}{N+1}$$

(5)

This results in:

$$\underline{x}\to {\omega }_{single}\mathrm{if}\frac{p\left(\underline{x}\right|{\omega }_{single})}{p\left(\underline{x}\right|{\omega }_{mix})}>N$$

(6)

Equation (6) is now the decision rule for a single-vs.-mixed-class decision where we assume that all individual classes appear with the same probability.

2.4. Experiment Design

We have implemented the DT design strategy with a Baysian classifier as described in Section 2.1, Section 2.2 and Section 2.3 and tested it on different simulated and real examples. For each example, we designed the numerically optimized DT and employed it for classification of the full image. Since we desire ML for the final result, we adjusted the balancing of prior probabilities according to Equations (5) and (6). For comparison, we also tested the numerically optimized DT with ML in each individual branch.

Furthermore, we performed an SFFS for traditional AAO classification and separated all classes in one step using the single selected feature set. To be able to compare results in terms of the AAO vs. DT approach, the AAO classifier is designed in exactly the same way as the DT, i.e., a multi-dimensional Bayesian classifier with Parzen density estimation using Gaussian kernel functions. It should be noted that any other classification method (support vector machine, neural network, etc.) could potentially be chosen. However, the same method should be employed for both AAO and DT to allow a comparison of the two approaches, which is independent of the underlying classifier.

To assess the final performance of a classifier in terms of classification accuracy, an independent validation set is needed. For the simulated images, we know all class labels by definition. We can therefore use all image pixels for validation that were not selected for the DT design and training. For the real datasets, we have split the selected ROIs for the different classes into training and validation set. During the DT design stage, cross-validation as described in Section 2.1 is performed within the training set, such that the performance of the final classifier can be assessed from a completely independent validation set.

3. Datasets

We have tested the numerically optimized DT on a variety of simulated and real datasets. The simulated data are used to demonstrate the robustness of the proposed method under controlled conditions with perfect validation data. For testing on real data we have used images from the spaceborne Sentinel-1 mission and an airborne, multi-channel SAR dataset with overlapping optical data. In the following, we present two representative examples. Since validation on the real datasets is much more reliable in the high-resolution airborne case with overlapping optical data, we choose to present this example as a detailed case study.

3.1. Simulated Test Dataset

To test the functionality and performance of the algorithm, we have generated several simulated examples with varying numbers of classes and features. In these simulated examples, the samples are simply drawn from class-dependent, multi-variate distributions and do not have a particular physical interpretation. In the case of SAR data, the different dimensions (features) could, e.g., represent intensities, polarimetric parameters, texture or other features. The test case presented here is an image with 1000 × 1000 pixels, 25 features and four classes separated in the four quadrant corners. We therefore refer to it as the C4-F25 dataset. The samples for each class are drawn from multi-variate Gaussian distributions. Mean values and variances of the distributions are designed such that the classes are partly separable in some of the features, while completely overlapping in other features. Furthermore, some features allow only to distinguish between two classes, while the remaining classes overlap.

We have randomly selected training data from the image with a varying number of training samples for each class. To ascertain that the training data is representative for the classes, we have run several tests using different training set sizes. We found the minimum required number of training samples per class to be approximately 400, with the exact number depending on the design of the distributions, i.e., the mean values and covariance matrices and the chosen dimensionality of the problem. The results shown in the next section were obtained with 1989, 1768, 1968 and 2139 training samples for classes $C_1$ to $C_4$, respectively. Remember that the different abundances of training samples are taken care of by correct balancing of probabilities, such that we achieve an ML classification (Section 2.3). Figure 4 shows one-dimensional histograms for some selected features of the training data set.

3.2. Airborne SAR Dataset: ICESAR

As a test case for airborne SAR data, we have chosen the ICESAR dataset acquired by AWI and DLR over sea ice in Fram Strait in March 2007. The dataset is described in detail in [26,36].

During the campaign, joint flights of AWI and DLR airplanes were carried out acquiring both radar (ESAR) and optical data. The ESAR measurements were recorded at C-band (dual-polarization, VH and VV) and at L-band (quad-polarization, HV, HH and VV) at incidence angles ranging from 26 to 55°. At a flight altitude of 3000 m, the resulting swath width is approximately 3 km.

The original ESAR images are delivered in single-look-complex (SLC) format and the measured reflectivity is given as radar brightness ${\beta }^0$. For the classification, we used final products in a ground-range multilook format with a pixel size of 1.5 m. To decrease the incidence angle sensitivity of the ground reflectivity, we converted the ${\beta }^0$-values to ${\gamma }^0$-values. Relationships between ${\beta }^0$, ${\gamma }^0$ and the backscattering coefficient ${\sigma }^0$ are given by

$${\beta }^0=\frac{{\sigma }^0}{sin\left({\theta }_1\right)}$$

(7)

and

$${\gamma }^0=\frac{{\sigma }^0}{cos\left({\theta }_1\right)},$$

(8)

where ${\theta }_1$ is the local incidence angle.

Optical images were recorded while repeating the flight track from the ESAR data at low altitudes. The RGB-layers in the visual representation of the optical data correspond to wavelength ranges 410 to 470 nm, 500 to 570 nm and 580 to 680 nm, respectively. The spatial resolution of the optical data is dependent on flight altitude and speed. It varies between 0.2 and 0.5 m across-track and 0.9 and 1.3 m along-track.

The maximum time lag between radar and optical measurements during the campaign was less than two hours and only minor variations of the ice cover characteristics can be recognized in the images, due to ice drift and deformation (Figure 5). However, the main ice situation during optical and SAR measurements was the same. We could therefore use a combination of optical data, SAR data and handheld photos taken during the flights to manually determine training regions for different ice classes. Only areas that appeared homogeneous were taken into account for these regions of interest (ROI). In total, we have defined six distinct classes (

Table 1. Classes defined from visual inspection of the ICESAR dataset, with corresponding color codes and number of samples.

	Description	Color Code	# Training Samples	# ROIs
Class ${\omega }_1$	Open water	dark blue	2398	3
Class ${\omega }_2$	Grey-white ice	light green	10,640	9
Class ${\omega }_3$	Level ice	black	14,233	8
Class ${\omega }_4$	Deformed ice	red	6356	12
Class ${\omega }_5$	Nilas	cyan	12,946	8
Class ${\omega }_6$	Grey ice	dark green	2342	5

). The acquired images and the manually defined ROIs for all classes are shown in Figure 5.

4. Results

In this section, we present the results obtained from our proposed algorithm and the comparison methods. We first give a general comment on computation times and then list the detailed classification accuracies, order of classes in the DT and selected feature sets for the previously introduced datasets.

Generally, the DT approach is more time consuming than the AAO approach, since it requires more operations. This is in particular true for the design stage. In the AAO approach, a six-class problem requires one single SFFS with six classes during the design stage. In the DT approach however, the design stage of the same six-class problem requires six SFFSs with two classes each in the first branch, five in the second branch, four in the third, three in the fourth and one in the fifth. Besides the dimensionality of the feature vector, the number of operations within a SFFS is proportional to the number of training samples and trained classes. In the DT, the number of training samples decreases with every branch, but the decrease is not known a priori and differs from case to case. For a six-class problem, the upper limit of the design stage computation time ratio for DT versus AAO is therefore $\frac{6\times 2+5\times 2+4\times 2+3\times 2+1\times 2}{1\times 6}=6.33$, meaning that the DT design and feature selection takes up to six times longer than the AAO feature selection. Once designed and trained, the forward classification for the DT approach is still more time consuming than the AAO approach, but with smaller difference. In the AAO approach, the forward classification stage of a six-class problem requires the evaluation of 6 PDFs for all patterns that are to be classified. In the DT approach, forward classification of the same six-class problem requires the evaluation of two PDFs in each branch. Again, we do not know a priori how many patterns will be removed from the data in each branch, so the upper limit for the ratio of forward classification times is $\frac{5\times 2}{6}=1.67$.

4.1. Results for Simulated Test Dataset

For the simulated example, all pixels that were not selected for training can be used as a validation set to estimate the final CA. The results for the C4-F25 dataset are summarized in

Table 2. Classification accuracy (%) for simulated test dataset C4-F25 for all-at-once (AAO) and decision-tree (DT) classifier.

	Total	Per-Class CA				Average
	CA	${\mathit{\omega }}_1$	${\mathit{\omega }}_2$	${\mathit{\omega }}_3$	${\mathit{\omega }}_4$	Per-Class CA
AAO	75.21	81.70	80.38	60.12	78.62	75.21
DT	78.78	84.50	82.61	68.84	79.16	78.78

. Our numerically optimized DT performs 3.5% better overall than a traditional AAO classifier, increasing total CA and average per-class CA from 75.21% to 78.78%. For individual classes, the improvement can be significantly larger (Table 2, class ${\omega }_3$).

Table 3. Single classes and selected features for each branch of the numerically optimized DT for simulated test dataset C4-F25.

DT Branch	Single Class	Selected Features
$B_1$	${\omega }_2$	$f_2$, $f_5$, $f_4$
$B_2$	${\omega }_1$	$f_5$, $f_{25}$, $f_{24}$, $f_2$
$B_3$	${\omega }_4$	$f_9$, $f_5$, $f_8$, $f_2$
AAO	—	$f_5$, $f_2$, $f_9$, $f_4$, $f_{13}$

shows the order of selected classes and the corresponding feature sets. The single feature set selected for AAO classification is {$f_5$, $f_2$, $f_9$, $f_4$, $f_{13}$}. Note that the class-specific feature sets can either be subsets of the AAO feature set (Table 3, Branch 1), or may contain features which are not in the AAO feature set at all (Table 3, Branch 2).

The total CA for the DT with ML in each individual branch is 76.60%, which is 2% lower than the total CA for our proposed approach of ML for the final result.

We show here only one representative example for the simulated datasets. Naturally, the exact scores and improvements in classification results differ, depending on dimensionality and design of the feature space as well as number and separability of the classes. However, in all 100 simulated cases, the optimized DT performs better than the traditional AAO classification. In all tested cases, improvements in average per-class CA range from 0.5% to 4%.

The DT with ML in each individual branch always performs worse than the final ML DT. In many cases, it also results in a lower CA than the traditional AAO classification, and hence correct balancing of the prior probabilities is important. After tuning of basic input parameters, the RF classifier performs similar to our optimized single DT. The best result was found with 100 trees and a maximum depth of 10, and achieved a total CA of 79.29% for the presented example.

4.2. Results for ICESAR Dataset

To estimate an independent CA for the ICESAR dataset, we split the pixels from the ROIs evenly into training and validation pixels. While the training set is used for kernel density estimation of the PDFs (see Section 2.2), the validation set is used for calculation of CA. The estimated CA and the order of selected classes with corresponding feature sets are summarized in

Table 4. Classification Accuracy (%) for ICESAR dataset for all-at-once (AAO) and decision-tree (DT) classifier.

	Total	Per-Class CA						Average
	CA	${\mathit{\omega }}_1$	${\mathit{\omega }}_2$	${\mathit{\omega }}_3$	${\mathit{\omega }}_4$	${\mathit{\omega }}_5$	${\mathit{\omega }}_6$	Per-Class CA
AAO	85.12	97.25	68.24	86.75	98.21	92.81	61.36	84.10
DT	87.48	99.75	75.43	87.40	98.57	93.69	65.76	86.77

and

Table 5. Single classes and selected features for each branch of the numerically optimized DT for ICESAR dataset.

DT Branch	Single Class	Feature Set
$B_1$	${\omega }_4$: deformed ice	$L_{HV}$, $L_{HH}$
$B_2$	${\omega }_1$: open water	$L_{HH}$, $C_{VV}$, $L_{VV}$, $L_{HV}$
$B_3$	${\omega }_5$: nilas	$C_{VV}$, $L_{HH}$, $L_{VV}$, $C_{VH}$
$B_4$	${\omega }_3$: level ice	$C_{VH}$, $C_{VV}$, $L_{HV}$
$B_5$	${\omega }_6$: grey ice	$C_{VV}$, $L_{HH}$, $L_{HV}$, $L_{VV}$
AAO	—	$L_{HH}$, $C_{VV}$, $L_{VV}$, $L_{HV}$, $C_{VH}$

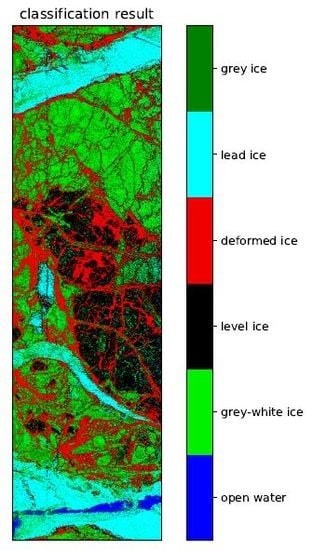
, respectively. Figure 6 shows the classification result from the DT classification.

Again, the DT performs better in terms of total CA as well as average per-class CA, with an improvement of about 2.5%. We also note that all individual classes score higher in the DT than in the AAO method. A particularly large improvement is achieved for grey-white and grey ice, with per-class CA increased by 7% and 4%, respectively (Table 4). Note also, that these are the lowest scoring classes overall, which are separated in the last branch of the DT.

We use five features in this example, and they all contain relevant information on some of the trained classes. Consequently, the single feature set for AAO classification contains all available features in order selected by the SFFS: {$L_{HH}$, $C_{VV}$, $L_{VV}$, $L_{HV}$, $C_{VH}$}. The class-specific feature sets of the individual DT branches are subsets of the single AAO feature set (Table 5).

5. Discussion

The tests on the simulated datasets show that the DT design works as expected. Class ${\omega }_2$ is selected as the individual class in the first branch, starting with feature $f_2$, followed by $f_5$ and $f_4$. This is in agreement with our design of the class distributions and can be confirmed by visual inspection of the histograms in Figure 4: In the 1D histograms, the most separable single class is clearly class ${\omega }_2$ in feature $f_2$.

Once the samples of class ${\omega }_2$ are removed from the dataset, class ${\omega }_1$ becomes the most separable, starting with feature $f_5$, followed by $f_{25}$ and $f_{24}$. Interestingly, the latter two features are not part of the commonly selected feature set in the traditional AAO classifier. This is due to different reasons: For feature $f_{24}$, there is large overlap between classes ${\omega }_1$ and ${\omega }_2$, and classes ${\omega }_3$ and ${\omega }_4$, respectively. Therefore, this feature does not contribute enough information to be selected in an AAO approach, where all classes are supposed to be separated simultaneously. For feature $f_{25}$, there seems to be too much overlap between the classes, although all distributions are slightly offset. However, after removing all samples from class ${\omega }_2$ in the first branch of the DT, class ${\omega }_1$ suddenly becomes significantly more separable in both features $f_{24}$ and $f_{25}$. This example demonstrates how the optimized DT allows us to make efficient use of features, which are not considered at all in a traditional multi-class classification.

Furthermore, we find that the numerically optimized DT performs about 3% better in terms of total CA than a corresponding AAO classifier. As shown earlier, this improvement comes at the cost of significantly longer computation times for classifier design and slightly longer times for forward classification. However, once an optimal design for a given problem such as ice type classification for a certain ice condition and from a particular sensor or combination of sensors has been decided, the most time consuming design stage does not need to be performed repeatedly for new images. As expected, demanding ML in each individual branch of the DT leads to reduced classification accuracy. This emphasizes the importance of proper balancing of the single and mixed-class prior probabilities according to Equation (5).

The tuned RF classifier achieves results comparable to those of the optimized single DT. While the total CA is slightly higher in the presented example, it is slightly lower for other simulated cases. However, the final class label of the RF is determined by a majority vote from a large number of trees in the forest. Our method uses only one single, multi-variate tree, with feature sets tailored towards individual classes. These class-specific feature sets of the single tree make the interpretation of individual features easier compared to the statistical interpretation of an RF. The direct connection between a particular set of features and class distinction is obvious.

An improved overall classification result for DT compared to AAO is also achieved for ice type classification from the airborne ICESAR dataset. As in the simulated cases, demanding ML in every single branch leads to lower total CA. The order of selected individual classes confirms that, at the relatively fine spatial resolution of 1.5 m, deformed ice is the individually best separable of the six classes given in Table 1. Furthermore, the selected features verify that L-band is superior to C-band measurements in the detection of deformed ice zones (Table 5, Branch 1). This is in agreement with results from earlier studies on the use of L-band for sea ice type classification, e.g., [26,28,36]. For open water we expect changing feature vectors, dependent on wind speed and direction relative to the open water leads in the ice cover. Visually, level ice and grey-white ice can be much better distinguished at C-band than at L-band, and level ice appears more inhomogeneous in the cross-polarized intensity channels than grey and grey-white ice (here we refer to intensity variations between the bright narrow deformation features). Both observations are reflected in the selected features (Table 5, $B_4$). This may be a consequence of beginning brine drainage, increasing volume of air bubbles and continued metamorphism processes in the snow layer.

A particularly large improvement in per-class CA was achieved for grey-white (7.2%) and grey ice (4.4%). Note that these are the classes with the overall lowest per-class CA, and thus the classes that are separated in the last branch of the DT (Table 5, $B_5$). Usually one expects that higher frequencies are more suitable to distinguish new and young ice. It is hence interesting to note that—although C-band VV-polarization is the first choice for distinguishing grey and grey-white ice—the additional use of L-band improves their separation. A more detailed analysis of the optimal choice of single features in the DT approach is beyond the scope of this study. We emphasize, however, that the selected features are related both to the characteristics of the single selected class and the remaining mixture of classes in each branch. In our example, this is valid for $B_1$–$B_4$.

6. Conclusions

We have introduced the fully automatic design of a numerically optimized DT classification algorithm that splits a multi-class classification problem with m classes into m-1 binary problems. In each branch of the DT, one class is separated from the other still remaining classes with an optimal set of features.

Tests on simulated datasets have demonstrated the capability of our algorithm to increase the total CA by 3.5% compared to traditional AAO classification. Improvement of 2.5% was achieved for classification of sea ice types from an airborne SAR dataset. Depending on class distributions and separability, individual classes may show larger improvement. In the presented sea ice example, CA for grey-white and for grey ice was improved by 7.2 and 4.4%. Since the absolute numbers of actual CA scores are highly dependent on the scene contents, we can only meaningfully compare to other methods using the same scenes. In our simulation and real world ICESAR examples, our proposed algorithm performs better than the more traditional AAO feature selection and Bayesian classification, and performs equivalently to the commonly used RF machine learning approach. At the same time our algorithm offers more direct interpretation of features and their potential to distinguish between particular classes.

The improved CA of the DT compared to the AAO approach comes at the cost of longer computation time. This is in particular true for the design and training stage, but to a lesser extent also for the forward classification stage. When time constraints are an essential part of the problem, as is the case in operational sea ice charting, the final choice of the classification strategy must be a trade-off between desired CA for single ice types and time constraints.