1. Introduction
Nitrogen (N) is a key input for plant development due to its role in the production of chlorophyll, which is crucial for photosynthesis [
1]. It has a significant role in attaining crop yield potential [
2] and quality [
3]. However, excessive N fertilization results in pollution, leading to negative environmental outcomes [
4]. Further, N use efficiencies are often low, which leads to non-optimal production costs [
5].
Rice N application can be optimized to meet desired targets [
6], such as yield, financial return on N cost [
7], quality and protein content [
8]. If too little N is available to the plants, the crop will not reach its yield potential [
9]. If too much N is applied, there is a risk that the crop will lodge, thus decreasing yield and increasing the time needed to harvest [
10]. Excess N also increases the risk of low temperature induced floret sterility, thereby reducing yield [
11] and also increases the risk of disease [
10]. Rice protein is determined by N status, with high levels of N resulting in lower cooked rice quality [
8].
A single pre-season N application is less effective than split application with mid-season topdressing [
12]. The Oryza-0 crop model has been used in simulations to optimize N application splits to optimize yield [
7]. The most effective time for a mid-season application is at the panicle initiation (PI) stage [
13], which occurs at the start of the reproductive phase of rice development, when the panicle begins to form in the base of the stem [
14]. Typically, a base N rate is applied at the start of the season, then tissue tests are done mid-season to determine additional N top-dressing rates [
15].
Pre-season soil tests have not proven to be a reliable way to determine paddy soil N requirements [
16,
17]. Detailed recommendations of N top-dressing rates as a function of PI N uptake and rice variety have been developed, utilising physical samples of plants at PI [
15,
18]. Site-specific management of rice N application has been shown to both improve yield [
19] and reduce total N applied [
20]. This improves farming profitability (due to reduced input costs and increased revenue) and environmental outcomes (due to reduced N loss to the atmosphere and water systems) [
21]. N requirements also vary spatially within paddies [
22], which motivates the application of spatially varying N at PI to match requirements. Studies of the application of such precision agriculture variable-rate techniques in wheat [
23] and sugarcane [
24] have shown improvement in N use efficiency.
There are a number of methods to determine N uptake at PI, with varying degrees of cost-effectiveness, practicability, accuracy and spatial resolution. Plant tissue samples can be collected and analyzed, however growers have little time and motivation to perform this task [
15]. When they do take samples, they are often only at a few points and so may not encompass the variability in their paddies. In addition, sample sizes are small in size (typically 0.2 m
), so sampling location can have a large impact on the degree to which the samples accurately represent the variation of N uptake across a site. Point measurements of rice N status can also be made using in-field sensors, such as SPAD meters [
1]. However, measuring individual leaves results in limited accuracy due to leaf-to-leaf variation, and many leaves must be sampled to represent plant N uptake adequately [
12]. These point sampling methods are labour intensive and therefore have seen limited adoption. Therefore, developing an operational remote sensing based method to determine N uptake is of great interest, as it captures spatial variation and may eliminate the need for field sampling. Typically industry desires variable N prescription maps with rates separated into 30 kg/ha classes (as aerial spreaders are probably not much more accurate than this and there is minimal impact on yield at PI topdressing rates less than 30 kg/ha [
15]). Therefore, N uptake prediction errors of less than 30 kg/ha are required [
18].
Canopy chlorophyll content has strong relationships with remotely sensed reflectances, and canopy nitrogen (N) content is strongly related to chlorophyll content [
25]. Thus, remotely sensed data can be used to predict canopy nitrogen content. Vegetation indexes using bands in the red-edge (740 nm), near infrared (790 nm) and green (550 nm) regions are particularly important to predict canopy N status [
26]. Chlorophyll content is strongly related to the red-edge and green absorption of leaves, while near infrared characteristics are related to structure and leaf thickness [
26].
Sensor types include optical cameras (3 bands—red, green blue) [
27], multispectral sensors (often adding near-infrared and red-edge bands to optical bands) [
21] and hyperspectral sensors [
28], which capture reflectance at over many narrow bands. Hyperspectral data was used to investigate determining N content at the heading stage [
29], and at the panicle formation stage [
28,
30]. Significantly different relationships between plant N status and hyperspectral data (measured in field with hyperspectral spectroradiometers) were found before and after heading [
31], explained by rice plant morphological differences. They found linear combinations of reflectance bands resulted in better prediction than ratio indexes or normalized difference indexes. The derivatives of reflectance with respect to wavelength may give greater accuracy across varieties, regions and seasons as shown in [
28]. Despite the accuracy and predictive power available from hyperspectral measurements, there are significant drawbacks including the cost of the sensors and data processing power required to derive useful models [
32]. These limit the current applicability of hyperspectral sensors to monitor rice crops for industry-wide commercial applications. However, these studies using hyperspectral sensors have shown the most important wavelengths for sensing N status, and therefore what wavelengths would be desired in multispectral sensors for this application. Multispectral sensors are relatively cost-effective, and have been used to predict rice N uptake with reasonable accuracy [
27], particularly when the sensor includes detection of the red-edge part of the spectrum.
Some studies have used hand-held or proximal sensors [
31]. Mounting sensors on unmanned aerial vehicles (UAVs) allows collecting within-field variability data in much less time than using proximal sensors [
21,
33,
34]. Some proximal sensing systems use active sensors, where the incident radiation is generated by the device. In contrast, most UAV systems utilise passive sensors, which rely on incident radiation from the sun and measure reflected radiation. Thus they require irradiance measurement or measurement of a known reflectance target in order to generate radiometrically corrected reflectance data [
35]. Thus, to generate accurate data, it is crucial to ensure sensors are calibrated accurately for current radiance conditions [
36], which may limit widespread grower adoption. The restrictive regulations on UAV operations, including line-of-sight and non-autonomous requirements, and the costs of acquiring images over larger areas currently render UAVs un-economical for large-area industry-wide application [
37]. Satellite-based multispectral data for rice N sensing is an alternative [
38,
39].
To achieve the goal of an operational remote-sensing based model to predict N uptake, a crucial factor is the stability of models over seasons, locations, varieties and management practices such as planting dates. Significant seasonal variation in models has been observed, attributed to differences in environmental conditions [
29]. These drivers, such as cumulative temperature and solar radiation, affect the dynamics of N uptake in rice [
40]. Soil N is also dynamic, and models that seek to address this were discussed in [
41]. Thus, it may be necessary to account for date differences between image captures and the dates that the actual N uptake is required.
Relatively few reports [
29,
30] train models on one or more seasons and test the model’s prediction accuracy on a separate season. If a model is required to predict future seasons N uptake from past data, it is important to separate model training, validation and testing data based on season, rather than randomly selecting points from all available seasons data. Another important factor for models is that they be interpretable and easily integrated into geographic information system (GIS) platforms. These goals may not be achieved if black-box machine learning methods are used, such as support vector machine (SVM) models and neural networks. Similar to [
21], we employed multi-variable linear regression using the Lasso regularization technique to select a subset of the most important predictors, while discarding less important predictors.
Our work is part of a project to provide an operational tool to Australian rice growers, to generate spatial maps of optimal N prescription rates to be applied at panicle initiation using remote sensing. It aims to provide a viable alternative to manual plant sampling, which has suffered limited industry adoption due to the time and effort required. Plant sampling also provides limited spatial resolution so is not useful for potential variable-rate applications. We assessed the stability of remotely sensed data over four seasons, two sites, four varieties and different sowing dates. Optimal combinations of data input variables to best predict N uptake were found, using data from WorldView satellite multispectral sensors, as well as climate, variety and management data. The WorldView sensors were chosen as they offer a combination of high spectral and spatial resolution. They are thus able to test our methodology of generating multi-season models of N uptake with fewer limitations from the sensors themselves. We draw conclusions on the best performance that can be expected in the study environment, and discuss potential transfer of the methodology to other, more cost effective, sensors.
4. Discussion
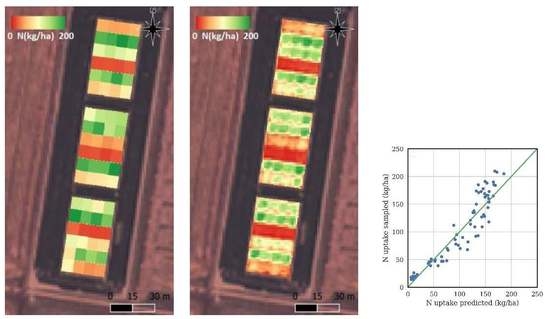
This study has demonstrated the accuracies that can be obtained using multi-spectral satellite data to predict the N uptake of rice at panicle initiation. This is an essential pre-requisite to developing an operational mid-season N topdressing recommendation tool for the rice industry, based on remote sensing.
Table 8 gives a summary of results from a selection of papers on predicting rice N uptake using remote sensing, for papers that report predicted N uptake root mean squared error (RMSE). The table assumes N uptake at jointing is similar to that at PI, and it shows the results for the best model formulation. The last column shows the worst case test season RMSE for the limited number of studies that test models on different seasons than those used to train the models.
Our work indicates that the model generation strategy critically depends on whether in-season sampling data is available. Complex multi-variable models predicting N uptake from remotely sensed data can be very accurate, providing in-season physical samples and remote sensing data is available for the season being predicted. In this case, previous studies have shown N uptake prediction errors as low as 7 kg/ha [
54], and many others around 12 kg/ha [
27,
28,
29]. However, these don’t consider the practically important application of predicting N uptake in new seasons for which sampling data is not yet available. With this limitation, we found N uptake RMSEs of better than 19 kg/ha with remote sensing data from four seasons as shown in
Table 5. Addition of management and climate data enabled prediction RMSE better than 15 kg/ha.
However, it is rarely the case that in-season data is available by the time predicted N uptake is needed to generate topdressing requirements, a factor which isn’t considered in most previous studies. The timing and logistics from image acquisition with simultaneous physical N uptake sampling, to model extraction from this data, to N uptake prediction, to N recommendation and finally to applying the top-dressing necessitates applying models extracted from previous data to new seasons. However, seasonal variability in models leading to inaccuracy in extrapolating models to new seasons was tested and noted by [
29] and [
30]. We likewise showed that simply extracting models using randomly selected training and validation data points from other seasons can result in very poor prediction of N uptake in a new season, with RMSEs greater than 100 kg/ha in some cases, as shown in
Table 6.
To solve this issue, we proposed a cross-validation procedure that uses training and validation data sets from separate seasons, which results in better generalization of N uptake prediction to new seasons. Testing across the four seasons of this study, we obtained RMSEs between 16.8–27.4 kg/ha. Notably, this was using multispectral sensors and from satellite platforms, which makes the methodology suitable for industry adoption.
The results illustrated a number of additional challenges to producing accurate N uptake models. The days between image acquisition and N uptake sampling affects model parameters, shown in
Table 4. Ideally, sampling should occur at the same time as image acquisition. This result shows the importance of having image capture close to the date at which N uptake is required if possible. It also motivates developing models for the dynamic change of N uptake with time and environmental conditions in case image acquisition must occur on a date significantly differently than the PI date. Ultimately, a model for the dynamics of N uptake with climate and time is desirable, so that the calculated N uptake from the image can be extrapolated to PI date. Models predicting soil N in flooded systems were reviewed in [
41]. These could be coupled with rice crop models to determine N uptake. The time and climate-dependent behavior of remotely sensed vegetation indexes that predict N uptake were shown in [
40]. Bringing remote sensing, environmental data and crop models together to improve accuracy of N uptake predictions may be an approach to improving N recommendations.
There are differences in the model of N uptake from remote sensed data from season to season that are difficult to model. More work is needed to determine the causes of these differences and how they can be incorporated into a model to improve the absolute accuracy to new seasons before sample data is available. Possible avenues for investigation include soil chemistry differences, water management differences, ponded water temperature differences, leaf area index differences at the image date (as ponded water may interact with canopy reflectance) and un-modelled climate effects [
55].
We investigated different combinations of remote sensing bands and spectral indexes. An important band for predicting N uptake on the WorldView satellites is nir2, at 860–1040 nm. Most multispectral sensors do not have an nir band with wavelengths this large, and some accuracy is lost using the lower wavelength nir band (770–895 nm) which is more common in a variety of sensors. We found models generated using four multispectral bands commonly found in sensors (green, red, red edge, near infrared) produced prediction errors 1–2 kg/ha higher than if all eight multispectral bands of the WorldView sensors were used. We found, in agreement with other works, the NDVI is a poor predictor of high values of N uptake, and indexes including the red-edge band are able to predict a greater range of values [
26]. We also showed that squaring the NDRE index follows the trend of N uptake closely.
We now consider the prospects of implementing a viable methodology of generating PI N uptake maps covering the rice industry in a given area. The cost of WorldView imagery is relatively high (though less in
$/ha than airborne data), and the minimum capture area is large. It may be feasible for commercial use if a large number of paddies are grouped in a small area (so the minimum area capture covers many fields), but may not be feasible for more sparsely distributed fields. Therefore, extending our multi-season N uptake prediction methodology to more cost-effective platforms is desirable. An additional consideration is that image acquisition needs to be arranged well in advance, so models forecasting PI date need to be accurate [
44]. There is also the risk of cloud cover on the selected acquisition date. Aerial platforms will remove limitations of image acquisitions on days with cloud cover and may offer more flexibility with late adjustments of image dates. UAVs offer an alternative for small areas, provided an experienced operator is available, who follows calibration protocols strictly. It would be useful to investigate the integration of models from various platforms and sensors in order to mitigate issues related to lack of availability of quality images from a single platform in a given season.
Following determination of N uptake at PI, recommendations of optimal N topdressing rates are needed. These recommendations may be generated using studies such as the one described in [
15], where plots were sampled for PI N uptake, and various topdressing rates were applied across plots. Then final grain yield results are used to generate tables of optimal PI N application as a function of PI N uptake. Variable rate topdressing resolution using aerial application is around 30 kg/ha. The multi-season model RMSE is as high as 27.4 kg/ha when predicting N uptake in an unseen season. However, given the remote sensing approach removes the labour associated with sampling, and the fact that it is unfeasible to sample enough points to adequately represent spatial variability, the remote sensing approach remains an attractive solution.