1. Introduction
Nitrogen (N) is a fundamental component of proteins and thus essential for any kind of living. Its relevance for the nutrition of plants and for the photosynthesis process is indisputable [
1]. Plants consist of a metabolic part with a high N concentration, such as leaves which are mostly responsible for photosynthetic processes, and a structural part with a low N concentration, such as the stem which is necessary for the plant architecture [
2]. During early growing stages, crop N demand primarily results from the leaf area expansion to initiate growth [
3]. When canopy closure is reached, plants compete for light and invest more N in stem elongation to place their leaves to the better-illuminated top layers [
4,
5]. Another role for the crop development can be attributed to the stem, as plants use stem N as source for grain N later in the growing season [
3]. If this storage is insufficient and further sources are missing, such as N released by natural leaf senescence or soil N, plants let leaves die off for the required N [
3]. This is likely to reduce the photosynthetic activity and inhibit growth. Hence, N plays the most important role in the fertilization of arable and forage cropping systems [
6].
The rapidly growing world population requires an increasing food production, which goes along with a rising use of N fertilizers [
7]. The global use of N fertilizer increased from ~10 Tg/year in the 1960s to ~80 Tg/year around 1990 [
8] and might reach ~190 Tg in 2020 [
9]. While aiming at increasing yield, it is frequently neglected that plants can assimilate N only up to a certain value. N losses into the environment has negative consequences, such as nitrous oxide emissions, nitrate leaching, or eutrophication [
8,
10,
11]. A strong research interest can hence be observed on the general N cycle, the N use efficiency (NUE) of plants, and the improvement and optimization of fertilization practices [
12,
13,
14,
15,
16,
17,
18].
A benchmark for quantifying the plant status at field scale is the crop-specific nitrogen nutrition index (NNI), defined as ratio between actual and critical N concentration [
19,
20]. The critical N concentration of dry biomass is defined as minimum N required for maximum growth [
21]. If N supply is not limited, the N concentration generally decreases while dry biomass increases across a growing season. This allometric relation can be expressed with a negative power function [
20]. A sequence of critical N concentration values can be plotted against dry biomass, which is then defined as crop-specific critical N dilution curve (NDC) [
19,
22,
23]. The NNI and NDC concept hence requires knowledge about dry biomass and N. Both values can either be determined destructively [
24] or, what is more common, estimated from proximal or remote sensing. Due to their non-destructive characteristics, these tools are highly attractive for precision agriculture or site-specific management and extensively investigated since the 1980s [
25,
26].
Remotely sensed spectral reflectance properties are known to be worthwhile for investigating vegetation [
27]. Numerous studies investigated the usability for determining NNI [
28,
29] or calculated vegetation indices (VIs) for estimating crop N [
30,
31,
32,
33,
34]. Dry biomass can also be estimated from VIs, but measurements are known to be affected by saturation effects at later growing stages [
35,
36,
37]. Major disadvantages of all passive spectral measurements are the dependency on solar radiation and the influence through atmospheric conditions, which require repeated calibrations during a campaign [
38,
39]. These problems can be avoided by using bidirectional spectrometers or active sensors [
30,
40,
41]. Further limiting factors are, however, the influence of differing soil properties, which is particularly important in the early growing period due to the low vegetation fraction [
42], and plant properties, such as the leaf inclination angle [
43]. Measurements with field spectrometers can also cover only small parts of the crop canopy. Based on their extensive research, Gastal et al. [
4] concluded that the NNI is more a research than a management tool and non‑invasive, cost-effective methods are required. They suggest chlorophyll measurements with a SPAD meter as promising tool for determining the N status. Various studies show its usability [
44] and propose it as tool for fertilizer recommendations [
45]. The amount of SPAD measurements is limited due to its handheld characteristics, which reinforces the general weakness of spectral measurements. An alternative robust approach for determining crop N at field scale is hence desirable.
The limitations of spectral sensing approaches, led to new research activities in crop monitoring, namely the sensing of structural properties such as crop height and crop density [
46,
47,
48]. At field scale, these traits can be derived by sensing methods which produce 3D data such as terrestrial laser scanning (TLS) [
49,
50] or photogrammetric processing using Structure from Motion (SfM) and Multi-View Stereopsis (MVS) [
51]. Other field studies measure with light curtains [
52] or ultrasonic sensors [
36,
53]. In a comparative study on different sensors, best results were achieved with laser scanning in comparison to an ultrasonic sensor and drone-based imaging [
54]. Several studies showed that dry biomass can be estimated from structural crop traits captured with TLS, drone-based imaging, or oblique stereo image acquisition [
55,
56,
57,
58,
59,
60,
61,
62,
63]. Only a few studies compared biomass estimations based on different sensors so far [
64]. From the existing ones, it can be summarized that structural estimators, such as crop height, outperform spectral ones [
47,
59,
65]. TLS and SfM/MVS approaches allow capturing large areas in a high spatial resolution. Hence, in‑field variabilities can be detected.
In summary, it is widely accepted that understanding processes and traits, which are involved in the N cycle of plants, are extremely important to optimize crop production [
4,
66]. Plant height is recognized as relevant trait [
67,
68], but until recent developments in proximal sensing, structural traits were hardly measurable in a sufficient spatial and temporal resolution at field scale. Manual measurements were laborious and prone to errors [
54]. The literature shows that dry biomass is estimable either from 3D or spectral measurements, considering the limitations for the latter. In contrast, to the best of the authors’ knowledge, crop N at field scale is only estimated from spectral information. Structural traits, determined from 3D data, are neglected so far. According to Seginer et al. [
69] the light competition among individual plants occurs early in the growing season, as canopy closure is rapidly reached in typically dense agricultural fields. Hence, potential height differences among individual plants or in‑field variations, which affect the amount of biomass, should be discernible. Along with the allometric relation between dry biomass and N concentration, the arising research question can be formulated as: Can the crop-specific N concentration at field scale be estimated from its indirect link to structural traits?
In a comprehensive study, Tilly et al. [
65] found that TLS‑derived plant height is a strong estimator for dry barley biomass (R
2 < 0.85) in contrast to VIs, which showed varying performance (R
2: 0.07–0.87). This new study further investigates this data set in terms of the stated research question as on the one hand, the quality and suitability of the data set was proven, but on the other hand, a so far unconsidered data set of destructively measured N was available. The overall aim of this study is to investigate whether the indirect link between structural traits and N concentration can be used for robust estimations at field scale. Two novel model designs are developed which investigate the interrelations between TLS‑derived crop surface height, dry biomass, and N concentration. Another VI-based model is established for comparison. A brief look is thrown on the relation of the estimators to the dry biomass and N concentration of individual plant organs.
4. Discussion
A first investigation of crop-specific models based on structural traits for indirectly estimating N concentration (%N) at field scale can be stated as overall aim of this study. Crop biomass and %N are two of the most important traits under investigation in precision agriculture. The usability of TLS‑derived crop surface height (CSH) or rather plant height as estimator for biomass has been demonstrated by several authors [
57,
58,
59,
60,
61,
62,
63]. An increasing number of studies on estimating biomass highlight the benefits of crop height as structural trait in comparison to spectral measurements [
47,
59,
65]. In contrast, %N is commonly estimated from spectral data [
4,
31,
32,
33]. It is well known that N is negatively related to biomass during the growing season, which, in turn, can be estimated from CSH. Based on this indirect link, a two-step model was designed for determining DBio based on CSH in the first step, followed by estimating %N with a nitrogen regression model (NRM) from the determined DBio in the second step. In addition, CSH was examined as estimator in one‑step NRMs and similar NRMs based on VIs were established.
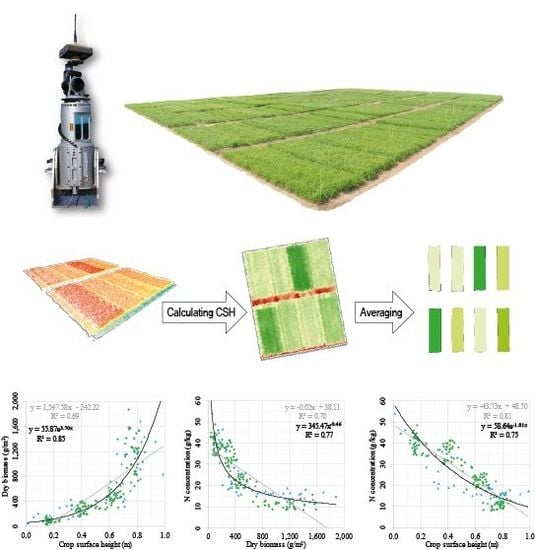
The development of CSH, DBio, and %N across the growing season showed that each crop trait has a certain pattern, which can be expressed with mathematic functions (R
2: 0.82–0.89). The relation between DBio and %N can be expressed with a power function (R
2: 0.77). Similar patterns were shown for winter barley [
24] and corn [
29]. That the allometric relation of %N vs. DBio during the vegetative growth can be expressed with a negative power function has early been recognized [
20] and is the fundament of the NNI and NDC concept. As shown in
Figure 4 [F], CSH vs. %N appears to be linearly (R
2: 0.81) or exponentially (R
2: 0.75) related, which supports the idea of using this structural trait as estimator for the N status of crops. Unfortunately, no comparable studies at field scale were found.
The applicability of biomass regression models (BRMs) based on CSH was demonstrated by Tilly et al. [
65]. In contrast, crop-specific NRMs are newly developed in this study and thus examined more closely with linear, exponential, and power functions. Since the NRMs of all approaches were similarly designed, the results can well be compared. A point in common of all NRMs is that only negligible differences between the three runs could be observed. This might be explained by the minor difference between the fertilizer treatments of only 40 kg/ha. In contrast, in the literature differences of 70 to 220 kg/ha can be found for common field experiments [
30,
41,
73,
84] or single experiments with extremely high rates of up to 420 kg/ha [
30].
Spectral approaches for determining %N are presented in different studies [
30,
31,
32,
33,
34]. In these studies, R
2 values between 0.50 and 0.80 were reached for different crops. The best performing VI in this study reached comparable results (R
2 < 0.70). Good results achieved with the R
760/R
730 and REIP in other studies [
30,
32,
40] could not be confirmed here (R
V2 < 0.35). Even though these VIs will be excluded from the model comparison, some explanations for their weak performance should be formulated. First, all other studies investigated wheat not barley. Furthermore, Erdle et al. (2011) [
40] and Baresel et al. [
30] investigated measurements within one growing stage and used bidirectional radiometer or active sensors. Similar to this study, Li et al. [
32] investigated different growing stages with a field spectrometer but obtained beside the quite good R
2 of 0.55 also weak results of 0.21 for the REIP. It can be summarized that the R
760/R
730 and REIP might be suitable for estimating crop %N. It should, however, be further investigated how prone these VIs are to effects such as saturation [
37], multiangular reflection [
85], leaf inclination angle [
43], or general atmospheric conditions. Further research should involve additional VIs, which were investigated for N content and N uptake, such as the red edge-based canopy chlorophyll content index [
86] or the optimum multiple narrow band reflectance model [
31]. Another approach that can be found in the literature are contour plot analyses. Conclusions of two studies are, however, that it is challenging to obtain the necessary information with two-band VIs due to the N dilution effect [
31] and that it will be difficult to develop a simple sensor that can determine the N concentration of plants with two or three bands for different growth stages [
32]. The presented approach based on structural data shall introduce an alternative method.
The power function produced the poorest results of the three function types, with the lowest R
2 and highest RMSE values. Furthermore, the weakest results were achieved with the two remaining VIs. For both VIs, best results were obtained with linear models, whereas the NRI performed slightly better (R
V2: 0.68–0.70) than the GnyLi (R
V2: 0.67–0.69). The NRMs based on DBio
mod yielded better results and performed best with exponential functions (R
V2: 0.81–0.82). The best and most robust results were obtained with the NRMs based on CSH (R
V2: 0.78–0.85). It should be further investigated whether the fusion of CSH and VIs in multivariate models improves the estimation, as it was observed for the BRMs [
65]. The benefit of the fusion of spectral and structural traits are also highlighted by other studies. The yield prediction of drought stressed barley for example could be improved [
73]. Acquiring 3D and spectral data with one sensor could therefore be worthwhile, which might be realizable with recently emerging hyperspectral laser scanners [
87]. First approaches of estimating rice leaf %N from multispectral and hyperspectral scanners can already be found [
88,
89]. These studies, however, only investigated the spectral information. Further research on the fusion of structural and spectral traits is required.
Quality, usability, and robustness of models can be assessed according to their accuracy and precision. Widely used metrics are the R
C2, R
V2, RMSE, and rRMSE. In case of the NRMs, R
C2 shows if CSH-based DBio models, CSH or VIs can express variations of %N and hence if it is a suitable indicator. R
V2 shows whether this relation is robust and transferable to independent data. It can well be used to compare the models among each other. RMSE and rRMSE are suitable for comparing the precision between the models. However, for evaluating the accuracy of NRMs for estimating %N, actual measurements must be considered. A major issue of across‑season estimations is the very varying %N. The rRMSE refers to the across‑season mean value, which can obviously hardly be used as reliable reference for the accuracy of the NRM at a certain point in time. As shown for the BRMs [
90], more credible values can be obtained with campaign‑wise separated analyses. Similar results are very assumable for the NRMs, which requires further research. The validity of the RMSE for time‑specific models must be further investigated to evaluate the usability of the approach for site-specific management. Beyond that, studies are needed on the transferability of the models to other field locations, years, or crops. Good results have already been achieved for the transferability of BRMs for paddy rice [
91]. However, it is known from the literature that the relationship between biomass and nitrogen is very different depending on the crop [
24,
92]. Accordingly, it can be assumed that NRMs must be calibrated crop-specific, as is the case for approaches with the nitrogen nutrition index (NNI). Novel machine learning approaches and algorithms, summarized as artificial intelligence, should also be taken into account for estimating crop traits [
93,
94,
95]. Approaches of estimating grass sward biomass [
96], quantifying rice N status [
97], or monitoring wheat leaf %N [
98] can already be found. As mentioned, an important point for site-specific management is the applicability of models at certain stages within the growing season. Analyses within one campaign were not very reliable with the available data set, due to the amount of data. Accordingly, further analyses with more extensive data sets are desirable for verifying the time-specific applicability of this approach.
The brief look at the relation between the estimators and individual plant organs suggests that CSH might be useful for estimating stem DBio and %N. The observed relation between CSH and leaf %N supports findings of Yin et al. [
99]. They found a good relationship between plant height of corn and leaf %N. Beside the known fact that more N is allocated to the metabolic actives leaves than to the stem, a similar negative slope of leaf %N and stem %N vs. CSH was found. As the quantification of metabolic and structural N demand of individual plant organs is required for example for growth simulation models [
5], further research on this is desirable. Moreover, this research can make an important contribution to understand the processes and traits, which are involved in the growth and N cycle of plants. For some crops, such as wheat, barley, and maize, the pre-anthesis ear and stem growth are somehow interlinked [
100]. From the rather good relation between ear DBio and stem %N (R
2: 0.78) or leaf %N (R
2: 0.77), it can be interpreted that these individual plant organs might be useful for yield approximations during the growing season. Further research on this is required.
Considering finally the applicability in the field, the main benefits of capturing structural traits in comparison to spectral measurements were stated in the introduction. A main disadvantage of acquiring spectral data with handheld spectrometers is the limitation to several discrete measurements. It has to be mentioned that in recent years several robotic system were developed as high-throughput mobile field platform [
101,
102]. Such platforms can accelerate the capturing process or even enable an autonomous data acquisition. Furthermore, approaches of a spatially resolved acquisition of spectral data can be found [
72,
103]. As these attempts are all quite new, the applicability and validity of the results has still to be investigated. Besides the development of appropriate sensors, the emergence of unmanned aerial vehicles (UAVs) as platform was a major milestone. As reviewed by several authors [
104,
105,
106], various studies attach digital cameras and multi- or hyperspectral imagers to UAVs for a nadir acquisition of surface properties. The size, payload, and stability of UAVs were rapidly improved through technical developments across recent years, which allows attaching heavier sensors, such as laser scanners. So far, such systems are occasionally used for capturing structural traits in forestry such as canopy height [
107], tree stem diameter [
108], or crown base height [
109]. Major disadvantages are the high cost and large data processing [
105]. Nevertheless, such UAV-based laser scanners would be beneficial for the acquisition of agricultural fields, as the nadir perspective should allow a deeper penetration of the vegetation and hence a more detailed capturing of the crop surface and structural traits. Crop density could also be captured from a nadir perspective. This is important in particular for the here investigated research question, as crop density influences the light competition process. This major process of plant growth can hence be examined more closely. Combining crop height and density information might allow precise and robust biomass and %N estimations. Finally, this research can have an influence on conventional agriculture, as sowing densities and fertilizer applications could be optimized.
5. Conclusions
Non-destructively estimating and monitoring crop biomass and nitrogen (N) concentration can support site-specific management. Studies show that dry biomass can be estimated by remotely sensing 3D or spectral information. In contrast, N estimations at field scale so far only base on spectral measurements, which are biased by illumination changes, vegetation fraction, plant properties, or saturation effects. This survey pursued a novel approach of estimating N concentration based on the indirect link to structural data. This link is based on the negative relationship between N and biomass, which can be estimated from crop height.
In two subsequent years, crop surface height was measured by terrestrial laser scanning (TLS), seven vegetation indices (VI) were calculated from field spectrometer measurements, and destructive measurements of dry biomass and N concentration were carried out. Based on the indirect link between crop surface height and N concentration, novel nitrogen regression models were established in three designs. The models based on modeled dry biomass and crop surface height reached R2 values of up to 0.85 and 0.82, respectively, and thereby outperformed the VIs (best R2: 0.70). The relation between crop surface height and N concentration of individual plant organs revealed that stem N showed a stronger dependency (R2: 0.81) in comparison to leaf N (R2: 0.69) and ear N (R2: 0.40). With the best performing VI, the NRI, considerably weaker results were achieved (R2 for stem, leaf, and ear N were 0.57, 0.68, and 0.18, respectively). This stem N is particularly important for plant growth, as it is one N source for the grain development.
In summary, these first results open perspectives for indirect models based on structural data as indicator for crop N concentration at field scale. Due to the crop-specific relationship between dry biomass and N concentration, it can be assumed that the models will have to be calibrated crop‑specific. Furthermore, the time-specific applicability of the models must be further investigated. Capturing 3D data with proximal sensing can be regarded as being more robust and comfortable to carry out in comparison to spectral measurements. Beside the data acquisition, the analysis of 3D data and determination of structural traits could be designed more user-friendly than the interpretation of spectral data. Hence, beside the usability as a research tool, TLS or photogrammetric approaches should be considered for improving non‑invasive and cost-effective N fertilizer management tools for farmers. For research purposes, such as monitoring plant-internal dynamics, investigating particular processes, or detecting diseases, the value of spectral information is indisputable. The fusion of 3D and spectral data can therefore be very beneficial.