Performance of Multi-GNSS Precise Point Positioning Time and Frequency Transfer with Clock Modeling

Abstract

Thanks to the international GNSS service (IGS), which has provided multi-GNSS precise products, multi-GNSS precise point positioning (PPP) time and frequency transfer has of great interest in the timing community. Currently, multi-GNSS PPP time transfer is not investigated with different precise products. In addition, the correlation of the receiver clock offsets between adjacent epochs has not been studied in multi-GNSS PPP. In this work, multi-GNSS PPP time and frequency with different precise products is first compared in detail. A receiver clock offset model, considering the correlation of the receiver clock offsets between adjacent epochs using an a priori value, is then employed to improve multi-GNSS PPP time and frequency (scheme2). Our numerical analysis clarify how the approach performs for multi-GNSS PPP time and frequency transfer. Based on two commonly used multi-GNSS products and six GNSS stations, three conclusions are obtained straightforwardly. First, the GPS-only, Galileo-only, and multi-GNSS PPP solutions show similar performances using GBM and COD products, while BDS-only PPP using GBM products is better than that using COD products. Second, multi-GNSS time transfer outperforms single GNSS by increasing the number of available satellites and improving the time dilution of precision. For single-system and multi-GNSS PPP with GBM products, the maximum improvement in root mean square (RMS) values for multi-GNSS solutions are up to 7.4%, 94.0%, and 57.3% compared to GPS-only, BDS-only, and Galileo-only solutions, respectively. For stability, the maximum improvement of multi-GNSS is 20.3%, 84%, and 45.4% compared to GPS-only, BDS-only and Galileo-only solutions. Third, our approach contains less noise compared to the solutions with the white noise model, both for the single-system model and the multi-GNSS model. The RMS values of our approach are improved by 37.8–91.9%, 10.5–65.8%, 2.7–43.1%, and 26.6–86.0% for GPS-only, BDS-only, Galileo-only, and multi-GNSS solutions. For frequency stability, the improvement of scheme2 ranges from 0.2 to 51.6%, from 3 to 80.0%, from 0.2 to 70.8%, and from 0.1 to 51.5% for GPS-only, BDS-only, Galileo-only, and multi-GNSS PPP solutions compared to the solutions with the white noise model in the Eurasia links.

1. Introduction

The global positioning system (GPS) has become an effective tool for time and frequency transfer since its first application in the 1980s [1]. A technique, called the common view (CV), is applied for International Atomic Time (TAI) comparison and provides an accuracy within several nanoseconds with a low-cost receiver [2,3]. The CV method utilizes single observed GNSS data with respect to the simultaneously observed GNSS satellites from two stations so as to cancel out the common satellite’s errors, which greatly simplifies the time transfer process. Thanks to the international GNSS service (IGS), which provides precise orbit and clock products, another technique, called the all-in view (AV), is employed for time transfer [3]. Unlike the CV technique, AV is not affected by the distance between station pair or baseline. The AV method allows a direct time comparison of any station on Earth with respect to the GPS system time (GPST) or the international GNSS service time (IGST) in the case where the IGS final ephemeris is used to compute the satellite orbits and clock offsets. Hence, it provides better results than the CV technique and was added to the Bureau International des Poids et Mesures (BIPM) software in September 2006. However, the code-only solutions have been utilized for time transfer in previous methods. For high-precision time and frequency, an approach, namely precise point positioning (PPP), is applied to time and frequency transfer [4]. Since September 2009, the GPS PPP approach has been utilized to compute time links for TAI in BIPM and is employed by 50% of more than 70 timing laboratories in the world for TAI and Coordinated Universal Time (UTC) computation [5,6]. GPS PPP has better short-term stability than the code-only method, as evidenced by the high-precision phase observations. The uncertainty of GPS PPP frequency comparison is approximately 1 × 10⁻¹⁵ on a 1-day average and approximately 1 ×10⁻¹⁶ on a 30-day average [6]. In addition, the type A uncertainty of GPS PPP is about 0.3 ns for time links in BIPM Circular T [5]. Moreover, GPS integer-PPP (IPPP) with precise products released by Centre National d’Etudes Spatiales (CNES) was investigated for frequency transfer and reached a frequency comparison with a 1 × 10⁻¹⁶ accuracy in several days [6,7,8].

With the rapid development of multi-GNSS, which includes GPS, GLONASS, BDS, and Galileo constellations, the multi-GNSS method is of great interest in the timing community. Ge et al. [9] investigated GLONASS-only PPP transfer and analyzed the handling strategies of inter-frequency code biases (IFCBs) in detail. The results indicated that the standard deviation (STD) of the difference between GLONASS-only PPP and GPS PPP was approximately 0.4 ns. Guang et al. [10] presented the progress of BDS time transfer at the National Time Service Center, Chinese Academy of Sciences (NTSC). They illustrated that the max STD of the difference between BDS CV and GPS PPP was up to 4 ns. Furthermore, BDS PPP with the products released by international GNSS continuous Monitoring and Assessment System (iGMAS) was first investigated by Ge et al. [11]. In addition, Tu et al. [12] proposed a triple-frequency un-combined (UC) BDS PPP time transfer model. They indicated that the accuracy and stability of the triple-frequency UC-PPP model was identical to the ionosphere-free PPP model. In addition, Galileo-only PPP time transfer was studied by Zhang et al. [13] with a prior constraint information. The STD of Galileo-only PPP was improved by 51.4 and 47.6%, respectively, with the troposphere zenith delay constraint and the station coordinates constraint. Moreover, multi-GNSS PPP time transfer was investigated by Zhang et al. [14]. The results showed that multi-GNSS time transfer outperformed single GNSS. However, their experimental data were insufficient to reflect the performance of long-term multi-GNSS time transfer.

Research focusing on multi-GNSS PPP time transfer considering the correlation of the receiver clock offsets between adjacent epochs is limited. In addition, multi-GNSS PPP time transfer with current multi-GNSS precise products has not been analyzed in detail. We therefore first analyze the multi-GNSS PPP with two different multi-GNSS products, GBM released by the German Research Centre for Geosciences (GFZ) and COD released by the Center for Orbit Determination in Europe (CODE). Multi-GNSS PPP with the receiver clock between-epoch constraint model [15] is then numerically presented.

We first review in brief the basic principles and technological aspects of the multi-GNSS PPP technique and describe PPP time transfer principles in detail. The experimental data and processing strategies are then presented. In the subsequent section, the experimental results are demonstrated. The conclusions are given in the final section.

2. Methodology

2.1. The Ionosphere-Free PPP Model

Generally, dual-frequency ionosphere-free (IF) combination PPP model is utilized to time and frequency transfer, which can be expressed as [11]

$$P_{IF}^S=\rho +d{t}_{r,IF}-d{t}_{IF}^S+d_{trop}+(d_{r,IF}-d_{IF}^S)+{\epsilon }_{r,P_{IF}}^S$$

(1)

$${\Phi }_{IF}^S=\rho +d{t}_{r,IF}-d{t}_{IF}^S+d_{trop}+{\lambda }_{IF}^S·(N_{IF}^S+b_{r,IF}-b_{IF}^S)+{\epsilon }_{r,L_{IF}}^S$$

(2)

where $P_{IF}^S$ and ${\Phi }_{IF}^S$ are the code and phase observation of satellites S in meters. $\rho$ is the geometric distance between the satellite S and receiver r. S represents GPS, GLONASS, BDS, and Galileo satellites in this study. $d_{r,IF}$ and $d_{IF}^S$ refer to the clock offsets of the receiver and satellite in meters, respectively. $d_{trop}$ represents the slant troposphere delay in meters. λ_IF is the ionosphere-free carrier wavelength on the frequency band; and N_IF is the float ambiguity in cycles. d_r,IF and $d_{IF}^S$ refer to the uncalibrated code delay (UCD) of the IF combination at the receiver and the satellite end in meters, respectively; $b_{r,IF}$ and $b_{IF}^S$ represent the uncalibrated phase delay (UPD) of the IF combination at the receiver and satellite end in cycles, respectively; ${\epsilon }_{r,P_{IF}}^S$ and ${\epsilon }_{r,L_{IF}}^S$ represent the code and phase observation noise.

Usually, the UCDs at satellite and receiver end will be absorbed by precise satellite clock and receiver clock offset, the reparameterization of Equations (1) and (2) is conducted as [15]

$$\{\begin{array}{l}d{\overline{t}}_r=d{t}_{r,IF}+d_{r,IF}\\ N_{IF}^S={\lambda }_{IF}^S\cdot (N_{IF}^S+b_{r,IF}-b_{IF}^S)-d_{r,IF}+d_{IF}^S\\ d{\overline{t}}_{IF}^S=d{t}_{IF}^S+d_{IF}^S\end{array}$$

(3)

where $d{\overline{t}}_{IF}^S$ and $d{\overline{t}}_r$ are the lumped satellite clock and the receiver clock offset in meters, respectively. $N_{IF}^S$ is the ambifutiy term. The parameter vector can be wrritten as

$$X={\left[x,d{\overline{t}}_r,d_{trop},N_{IF}^S\right]}^T$$

(4)

where x is the vector of the receiver position increments relative to the a priori position.

For single GNSS PPP, including GPS-only, GLONASS-only, BDS-only, and Galileo-only methods, Equations (1)–(4) can be applied directly. For convenience, GPS, GLONASS, BDS, and Galileo will be represented by G, R, C, and E in our work.

For multi-GNSS combined PPP, such as GPS + GLONASS + BDS + Galileo, additional biases, which are commonly called inter-system biases (ISBs) [16,17,18], should be considered. Multi-GNSS has a different satellite system time scale. In this contribution, the GPS time scale is selected as the common reference satellite time scale. The receiver clock offset in GLONASS, BDS, and Galileo will be conducted with the sum of the receiver clock offset of GPS satellites and the corresponding ISBs parameters, respectively.

Hence, the multi-GNSS combined PPP observation equation for time and frequency transfer can be expressed as

$$\{\begin{array}{l}{P}_{IF}^G=\rho +d{\overline{t}}_{r,IF}-c·d{\overline{t}}_{IF}^G+d_{trop}+{\epsilon }_{r,P_{IF}}^G\\ P_{IF}^R=\rho +d{\overline{t}}_{r,IF}+IS{B}^{GR}-d{\overline{t}}_{IF}^R+d_{trop}+{\epsilon }_{r,P_{IF}}^R\\ P_{IF}^C=\rho +d{\overline{t}}_{r,IF}+IS{B}^{GC}-d{\overline{t}}_{IF}^C+d_{trop}+{\epsilon }_{r,P_{IF}}^C\\ P_{IF}^E=\rho +d{\overline{t}}_{r,IF}+IS{B}^{GE}-d{\overline{t}}_{IF}^E+d_{trop}+{\epsilon }_{r,P_{IF}}^E\\ {\Phi }_{IF}^G=\rho +d{\overline{t}}_{r,IF}-d{\overline{t}}_{IF}^G+d_{trop}+N_{IF}^G+{\epsilon }_{r,L_{IF}}^G\\ {\Phi }_{IF}^R=\rho +d{\overline{t}}_{r,IF}+IS{B}^{GR}-d{\overline{t}}_{IF}^R+d_{trop}+N_{IF}^R+{\epsilon }_{r,L_{IF}}^R\\ {\Phi }_{IF}^C=\rho +d{\overline{t}}_{r,IF}+IS{B}^{GC}-d{\overline{t}}_{IF}^C+d_{trop}+N_{IF}^C+{\epsilon }_{r,L_{IF}}^C\\ {\Phi }_{IF}^E=\rho +d{\overline{t}}_{r,IF}+IS{B}^{GE}-d{\overline{t}}_{IF}^E+d_{trop}+N_{IF}^E+{\epsilon }_{r,L_{IF}}^E\end{array}.$$

(5)

The parameter vector can be wrritten as

$$X={\left[x,d{\overline{t}}_r,IS{B}^{GR},IS{B}^{GC},IS{B}^{GE},d_{trop},N_{IF}^G,N_{IF}^R,N_{IF}^C,N_{IF}^E\right]}^T.$$

(6)

The user can obtain the local time T and the reference time by multi-GNSS PPP directly with the hardware delay calibration. The time difference between two or more stations can then be calculated by

$$\Delta T=T_1-T_2=(T_1-ref)-(T_2-ref)=d{t}_1-d{t}_2$$

(7)

where ref is the reference time of the satellite, and $\Delta T$ represents the time difference between two stations. 1 and 2 refer to two different stations.

2.2. Receiver Clock Estimation with the Between-Epoch Constraint Model

Usually, the receiver clock offset is estimated with the white noise model. In addition, the correlation of clock offsets between adjacent epochs is not considered in multi-GNSS PPP time transfer. In our work, a between-epoch constraint model [15] was applied to estimate the receiver clock offset. The a priori noise variance is calculated by the Allan variance. Note that the Allan variance is calculated by using the receiver clock offset derived from GPS PPP with the IGS final product [19] herein. When the white phase modulation noise q₀, the white frequency modulation noise q₁, the random walk frequency modulation noise q₂, and the random run frequency modulation noise q₃ are all considered, the Allan variance ${\delta }_{Allan}^2\left(\tau \right)$ can be written as [20]

$${\delta }_{Allan}^2\left(\tau \right)=3q_0{\tau }^{-2}+q_1{\tau }^{-1}+\frac{q_2\tau }{3}+\frac{1}{20}{q}_3{\tau }^3$$

(8)

where $\tau$ is the time interval. We should initially estimate q₀, q₁, q₂, and q₃ by least squares, when the sample rate of the user is higher than the sample rate of the GPS PPP solutions using IGS final products and then calculate the Allan variances at the sample rate of the user. Finally, the a priori noise variance $Q_w$ is determined [15], which can be expressed as

$$Q_w={\left({\delta }_{Allan}(\tau )·\tau ·c\right)}^2$$

(9)

where c is the speed of light.

3. Experimental Data and Processing Strategies

To validate how the multi-GNSS PPP time transfer performs with the between-epoch constraint model, observation data with a 30 s sample rate from 6 stations were chosen. Days of Year (DOYs) 182–202 in 2018, as listed in

Table 1. The summary of the selected stations from timing laboratories.

Station	Receiver	Antenna	Clock
NTSC	SEPT POLARX5TR	SEPCHOKE_MC	H-MASER
BRUX	SEPT POLARX4TR	JAVRINGANT_DM	H-MASER
PT11	SEPT POLARX4TR	LEIAR25.R4 LEIT	H-MASER
HOB2	SEPT POLARX5	AOAD/M_T	H-MASER
USN8	SEPT POLARX4TR	TPSCR.G5	H-MASER
HARB	TRIMBLE NETR9	TRM59800.00	CESIUM

, are covered. Note that NTSC, PT11, and BRUX are located at timing laboratories. All stations are connected to a high-precision atomic clock. Taking NTSC as the center node, time transfer solutions of 5 time links were designed, as distributed in Figure 1.

GPS-only, BDS-only, Galileo-only, and combined GPS + GLONASS + BDS + Galileo PPP methods in static modes were performed. Multi-GNSS precise orbit and clock products by GFZ and CODE were held fixed. The sampling intervals of precise orbit and clock products were 5 min and 30 s, respectively, for GBM and COD. The detailed PPP processing strategies are presented in

Table 2. Details of precise point positioning (PPP) processing strategies.

Item	Strategies
Observable	Ionosphere-free combination
Satellite orbit and clock	GBM, COD
Satellites	GPS, GLONASS, BDS, Galileo
PCO/PCV	Corrected (igs14.atx)
Tides	Corrected [21]
Relativistic effect	Corrected [21]
Sagnac effect	Corrected [21]
Phase windup	Corrected [22]
Troposphere	Estimated as a random walk process
Ambiguity	Estimated as constant
Elevation angle cutoff	10°
Station coordinate	Estimated as constant
Receiver clock offset	Estimated with white noise model; Estimated with between-epoch constraint model
Reference	IGS final receiver clock products
ISB	Estimated as white noise

. The elevation-dependent weighting for the observations was applied. The measurement error ratio between code and carrier phase observations was set to 100. Note that GPS, GLONASS, BDS, and Galileo will be represented by G, R, C, and E in this study.

First, multi-GNSS PPP time transfer performances with different precise products are compared. The performance of multi-GNSS PPP time transfer with/without the between-epoch constraint model is then numerically analyzed.

4. Results

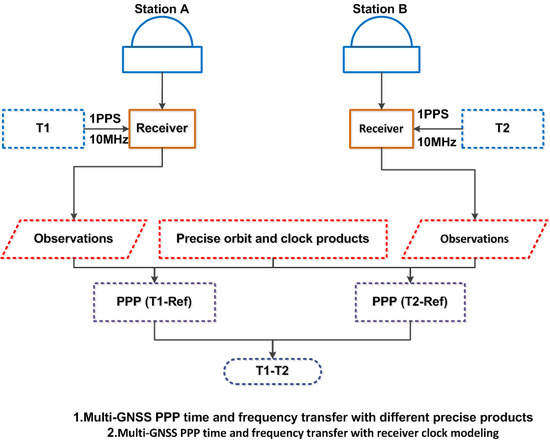
This section starts with the performance of multi-GNSS PPP time transfer with different precise products released by GFZ and CODE, as well as the advantage of multi-GNSS PPP with respect to a single satellite system. Following that is an evaluation of multi-GNSS PPP time transfer with a between-epoch constraint model with respect to that with a white noise model.

4.1. Multi-GNSS PPP Time Transfer with Different Precise Products

As an example, we show in Figure 2 the clock offsets for single- and multi-GNSS models on BRUX using GBM and COD products. Furthermore, the clock offsets for single- and multi-GNSS models on HARB using GBM and CODE products are displayed in Figure 3. These results suggest four findings.

First, the results of GPS-only, BDS-only, Galileo-only, and multi-GNSS PPP using GBM and COD products present a system bias, which is evidenced by the fact that the reference times of GBM and COD products are different. Although the reference time of different products is not the same, the accuracy of time transfer is not affected because the reference time is eliminated. In addition, GPS and BDS PPP solutions with the same products also show a system bias, which is evidenced by the fact that a hardware delay is related to the signals and absorbed by the receiver clock offset. Second, the clock offsets of BDS-only and Galileo-only PPP using GBM and COD products all show an apparent jump at each day, while GPS PPP solutions do not. This may be explained by the fact that the reference times of BDS-only and Galileo-only products in GBM and COD are not aligned to GPST or a unified time scale. Third, BDS PPP solutions using GBM products perform better than those using COD products. The reason is that COD products have no GEO satellite orbit or clock products. Additionally, the performance of GPS-only PPP is better than that of BDS-only PPP at the Eurasian links and shows the same characteristic in Asia-Pacific, as suggested by the fact that the receiver in Europe observed fewer BDS-2 satellites. BDS-3 satellites have officially provided global services since 27 December 2018. With the upgrading of the receiver hardware and the development of multi-GNSS precise products, we expect BDS to achieve better results. Fourth, compared with GPS-only, BDS-only, and Galileo-only PPP solutions, multi-GNSS PPP is more stable and has less noise.

Figure 4 and Figure 5 depict the clock difference in single-system and multi-GNSS models using GBM and COD products on BRUX-NTSC and HARB-NTSC, respectively. Taken together, we make two remarks here. First, the system bias disappears when using different precise products due to the elimination of the reference time. Second, the variations in GPS-only, Galileo-only, and multi-GNSS PPP time transfer values are in good agreement with each other, while BDS-only performs worse on the BRUX-NTSC time link. Interestingly, the variations in time transfer values are in good agreement with the results for each scheme on the HARB-NTSC time link. The major reason for this may be explained by Figure 6 and Figure 7, depicting the number of satellites and the time dilution of precision (TDOP) for GPS, BDS, Galileo, and multi-GNSS methods at the BRUX and NTSC stations on DOY 182, 2018. For the 10° elevation cut-off, the mean number of satellites is 24.1 for multi-GNSS, 8.8 for GPS, 4.1 for BDS, and 5.2 for Galileo at BRUX. The number of available satellites in the multi-GNSS is more than doubled, as compared with GPS-only. However, this number is the lowest in BDS, which directly affects the accuracy of the results. For the NTSC station, the mean values are increased from 8.2 (GPS-only) to 28.2 (multi-GNSS). More importantly, the mean number of BDS is 9.8. Hence, we can conclude that the number of BDS is analogous to GPS in Asia-Pacific. In addition, the receiver clock offset is of interest in the timing community. The multi-GNSS will improve the accuracy by improving the tracking with a reduction in TDOP. The mean TDOP is 1.2 for GPS, 1.5 for BDS, 2.5 for Galileo, and 0.5 for multi-GNSS at the NTSC station. In addition, the mean TDOP is 1.0 for GPS, 4.2 for BDS, 1.8 for Galileo, and 0.5 for multi-GNSS at BRUX. The TDOP is clearly improved by multi-GNSS, as compared to a single system. Hence, the multi-GNSS solution exhibits improved robustness compared to individual single-system solutions.

To further quantify this agreement, we calculated the root mean square (RMS) value for the smooth result, which is usually employed in the timing community [23]. Unlike precise positioning, the two external time and frequency references are equipped with two receivers of one time link, which affects the performance evaluation for different time transfer schemes. The vondrak smoothing method [23] is applied to provide the corresponding RMS values. Time link residuals compared with vondrak smoothing values using COD and GBM products are presented in

Table 3. Time link residuals compared with vondrak smoothing values using COD products (ns).

	GPS	(%)	BDS	(%)	Galileo	(%)	Multi
BRUX-NTSC	0.003	2.0	0.082	96.6	0.006	53.7	0.003
PT11-NTSC	0.003	3.6	0.017	79.9	0.007	55.0	0.003
USN8-NTSC	0.006	18.2	0.114	95.7	0.009	48.5	0.005
HARB-NTSC	0.047	3.5	0.066	31.1	0.048	6.5	0.045
HOB2-NTSC	0.090	1.2	0.091	2.2	0.091	1.6	0.089

and

Table 4. Time link residuals compared with vondrak smoothing values using GBM products (ns).

	GPS	(%)	BDS	(%)	Galileo	(%)	Multi
BRUX-NTSC	0.003	7.4	0.053	94.0	0.006	46.9	0.003
PT11-NTSC	0.003	5.2	0.037	91.4	0.007	57.3	0.003
USN8-NTSC	0.007	2.6	0.112	93.7	0.010	27.9	0.007
HARB-NTSC	0.046	1.4	0.065	29.9	0.046	1.6	0.046
HOB2-NTSC	0.091	1.4	0.097	7.6	0.091	0.9	0.090

, respectively. In addition, the improvement of multi-GNSS with respect to GPS-only, BDS-only, and Galileo-only methods is clearly listed. Combining Table 3 and Table 4, we have two key findings. First, the performances of time transfer with single-system or multi-GNSS PPP using GBM and COD products are in good agreement with each other. Hence, we can conclude that multi-GNSS PPP transfer with GBM and COD products show the same performance. Second, we can clearly see that multi-GNSS PPP solutions have less noise compared to the single-system solutions, especially with respect to the BDS-only and Galileo-only results at the Eurasia time links, while it is relatively small in the Asia-Pacific time links. For the Eurasia time links, maximum improvements of the multi-GNSS solutions are up to 18.2%, 96.6%, and 53.7% compared to the GPS-only, BDS-only, and Galileo-only solutions, respectively, using COD products. With respect to the Asia-Pacific time links, the maximum improvements of the multi-GNSS solutions are up to 3.5%, 31.1%, and 6.5% compared to the GPS-only, BDS-only and Galileo-only solutions, respectively. For single-system and multi-GNSS PPP with GBM products, maximum improvements of multi-GNSS solutions are up to 7.4%, 94.0%, and 57.3% compared to the GPS-only, BDS-only and Galileo-only solutions, respectively, for all results.

In Table 3 and Table 4, (%) indicates the improvement of multi-GNSS with respect to the GPS-only, BDS-only and Galileo-only solutions.

The time link is equipped with two different time and frequency references. Therefore, it is complicated to evaluate the performance of the PPP time transfer due to the absence of an absolute standard for comparison. Hence, the Allan deviation (ADEV) was applied to obtain the frequency stability [12,15] and to further assess the performance of the single-system and multi-GNSS solutions. Figure 8 presents the frequency stability of the single-system and multi-GNSS solutions for four time links using COD products. In addition, the percentage improvement of multi-GNSS stability over individual systems is displayed in Figure 9 for different average times. Taken together, we obtain three findings here. First, the stability of BRUX-NTSC and PT11-NTSC is better than that of HARB-NTSC and HOB2-NTSC, as evidenced by the fact that the stability of time links is determined by the performance of atomic clocks. We also see that atomic clocks with different performances are equipped at different stations in Table 1. In addition, NTSC, PT11, and BRUX are located in timing laboratories. Second, the performance of GPS PPP is better than Galileo- and BDS-only PPP solutions in the Eurasia time links [10] and is similar to those in Asia-Pacific time links. This further validates our previous conclusions. Third, the improvement in the multi-GNSS ranges from 0.1 to 20.3% compared to the GPS-only solution. The multi-GNSS presents a significant improvement over the BDS-only solution in the Eurasia time links. The maximum improvement is up to 84%. For the Galileo-only solution, the improvement ranges from 0.1 to 45.4%.

Figure 10 depicts the frequency stability of single-system and multi-GNSS solutions for four time links using GBM products. The percentage improvement of multi-GNSS stability over individual systems is displayed in Figure 11 for different average times. The results using GBM products are analogous to those using COD products. The improvement in the multi-GNSS ranges from 0.04 to 17.4% compared to the GPS-only solution at different average times. The multi-GNSS presents a significant improvement over the BDS-only solution in the Eurasia time links. The maximum improvement is up to 87.2%. For the Galileo-only solution, the improvement ranges from 1.1 to 49.2%, the averages are 27.3%, 30.1%, 5.6%, and 3.4% for PT11-NTSC, BRUX-NTSC, HOB2-NTSC, and HARB-NTSC, respectively.

4.2. Multi-GNSS PPP Time Transfer with the Between-Epoch Constraint Model

In this subsection, based on the multi-GNSS PPP method and the between-epoch constraint model, two schemes were designed. For convenience, the two schemes summarized in

Table 5. Summary of the multi-GNSS PPP time transfer schemes.

Items	Description
scheme1	PPP time and frequency transfer based on GBM and COD final products; receiver offset estimated with the white noise model.
scheme2	PPP time and frequency transfer based on GBM and COD final products; receiver offset estimated with the between-epoch constraint model.

are marked as scheme1 and scheme2.

Figure 12 and Figure 13 show the clock difference of scheme1 and scheme2 with single-system and multi-GNSS models on BRUX-NTSC and HARB-NTSC, respectively, using COD products. Combining Figure 12 and Figure 13, two findings are marked here. First, scheme1 and scheme2 have no system bias and have good consistency, which illustrates the feasibility of our model. Second, interestingly, our method can significantly improve the performance of BDS PPP in the Eurasia link because the receiver in the European region observed a relatively small number of BDS satellites, and the geometry strength is not very high. The between-epoch constraint model was employed to estimate the clock offset in scheme2, which will improve the strength of the equation. In addition, some BDS satellites have lower elevation angles in the European region. The between-epoch constraint model reduces the amount of noise absorbed by the receiver clock offset and improves the accuracy of BDS PPP time transfer.

In order to analyze the two schemes, we used the results of vondrak smoothing as a reference. The RMS values of the difference between the two schemes and the smoothing results were obtained. Results are presented in

Table 6. Time link residuals of scheme1 and scheme2 compared with vondrak smoothing values using COD products (ns).

	GPS			BDS			Galileo			Multi
	1	2	(%)	1	2	(%)	1	2	(%)	1	2	(%)
BRUX-NTSC	0.003	0.002	41.9	0.082	0.060	26.0	0.006	0.005	24.2	0.003	0.002	15.0
PT11-NTSC	0.003	0.002	45.3	0.017	0.010	39.3	0.007	0.006	22.9	0.003	0.003	20.4
USN8-NTSC	0.006	0.004	36.5	0.114	0.080	30.1	0.009	0.007	30.7	0.005	0.003	46.9
HARB-NTSC	0.047	0.004	92.2	0.066	0.058	11.8	0.048	0.045	6.6	0.045	0.004	90.9
HOB2-NTSC	0.090	0.055	39.0	0.091	0.072	21.3	0.091	0.051	43.3	0.089	0.053	40.2

and

Table 7. Time link residuals of scheme1 and scheme2 compared with vondrak smoothing values using GBM products (ns).

	GPS			BDS			Galileo			Multi
	1	2	(%)	1	2	(%)	1	2	(%)	1	2	(%)
BRUX-NTSC	0.003	0.002	42.4	0.053	0.041	23.0	0.006	0.004	33.2	0.003	0.002	30.3
PT11-NTSC	0.003	0.002	37.8	0.037	0.026	27.7	0.007	0.005	29.0	0.003	0.002	26.6
USN8-NTSC	0.007	0.005	24.0	0.112	0.038	65.8	0.010	0.006	39.3	0.007	0.005	26.8
HARB-NTSC	0.046	0.004	91.9	0.065	0.058	10.5	0.046	0.045	2.7	0.046	0.006	86.0
HOB2-NTSC	0.091	0.056	38.2	0.097	0.068	30.5	0.091	0.052	43.1	0.090	0.056	38.1

. The main conclusion to be drawn from Figure 12 and Figure 13, in conjunction with Table 6 and Table 7, is straightforward. It is clear that scheme2 contains less noise compared to scheme1, whether a single-system model or a multi-GNSS model is used. The improvement of scheme2 ranges from 36.5 to 92.2% compared with scheme1 for the GPS-only solution. Compared to scheme1, the solutions of scheme2 are improved by 11.8–39.3%, 6.6–43.3%, and 15.0–90.9% for BDS-only, Galileo-only, and multi-GNSS solutions. More interestingly, the performance of scheme2 using GBM products is similar to that using COD products. This can explain that our approach is suitable for different products. The solutions of scheme2 are improved by 37.8–91.9%, 10.5–65.8%, 2.7–43.1%, and 26.6–86.0% using the GPS-only, BDS-only, Galileo-only, and multi-GNSS solutions.

In Table 6 and Table 7, 1 and 2 represent scheme1 and scheme2, respectively. (%) is the improvement of scheme2 compared to scheme1.

As mentioned previously, an absolute standard for comparison is lacking. Here, ADEV is considered again to further assess how well our approach performs for multi-GNSS PPP time and frequency transfer. Figure 14 and Figure 15 show the Allan deviation of scheme1 and scheme2 on PT11-NTSC and HOB2-NTSC, respectively, with single-system and multi-GNSS models using COD products. Overall, the results show that in each panel the frequency stability is notably improved, especially for short-term stability, and that, in accordance with our expectation, each result using single-system or multi-GNSS models exhibits different degrees of improvement. We surmise that this may be because, applying our approach, the noise of the clock offset is reduced significantly. To further quantify this improvement, the improvement of the four time links was calculated, and the results are displayed in Figure 16. A significant improvement is clear in the Eurasia links, especially for the BDS-only and Galileo-only models. This further explains that our approach performs better than scheme1, especially for the few observed satellites. For the Eurasia links, the improvement of scheme2 ranges from 0.2 to 51.6%, from 3 to 80.0%, from 0.2 to 70.8%, and from 0.1 to 51.5% for the GPS-only, BDS-only, Galileo-only and multi-GNSS PPP solutions compared to scheme1. In addition, the performances of scheme2 are improved by 0.3–39.9%, 0.1–52.5%, 0.2–47.8%, and 0.1–40.7% for GPS-only, BDS-only, Galileo-only, and multi-GNSS PPP solutions compared to scheme1 in Asia-Pacific.

Figure 17 and Figure 18 show Allan deviation of scheme1 and scheme2 on BRUX-NTSC and HARB-NTSC, respectively, with single-system and multi-GNSS models using GBM products. Like the solutions using COD products, it follows that, in each panel, the frequency stability is significantly improved, especially for short-term stability. The improvement of the four time links was calculated, and the results are displayed in Figure 19. For the Eurasia links, the improvement of scheme2 ranges from 0.1 to 50.4%, from 0.1 to 74.2%, from 0.2 to 72.9%, and from 0.9 to 49.1% for GPS-only, BDS-only, Galileo-only, and multi-GNSS PPP solutions compared to scheme1. In addition, the performances of scheme2 are improved by 0.3–39.2%, 0.4–41.0%, 0.2–47.4%, and 0.1–38.4% for GPS-only, BDS-only, Galileo-only, and multi-GNSS PPP solutions compared to scheme1.

5. Conclusions

Multi-GNSS precise point positioning (PPP) time and frequency transfer has become a hot topic in the timing community. However, research investigating the multi-GNSS PPP time and frequency transfer with different precise products is limited. Moreover, clock offset parameters in multi-GNSS PPP are estimated as white noise (scheme1). This method will not consider the correlation of the receiver clock offsets between adjacent epochs.

In this work, multi-GNSS PPP time and frequency with different precise products is first compared in detail. An approach for multi-GNSS time and frequency transfer is then employed, where the clock offset is estimated with a between-epoch constraint model (scheme2) rather than a white noise model for further improving the performance of multi-GNSS PPP time and frequency transfer. Root mean squares (RMSs) and Allan deviation (ADEV) were applied to evaluate the performance of multi-GNSS PPP. The analysis of the results obtained three conclusions.

First, the GPS-only, Galileo-only, and multi-GNSS PPP solutions show similar performances using GBM and COD products, while BDS-only PPP using GBM products is better than that using COD products.

Second, the maximum improvements of multi-GNSS solutions is up to 18.2%, 96.6%, and 53.7% compared to GPS-only, BDS-only, and Galileo-only solutions, respectively, using COD products for the Eurasia time links. With respect to the Asia-Pacific time links, the maximum improvement of multi-GNSS solutions is up to 3.5%, 31.1%, and 6.5% compared to GPS-only, BDS-only, and Galileo-only solutions, respectively. For stability, the improvement in the multi-GNSS ranges from 0.1 to 20.3% compared to the GPS-only solution. The multi-GNSS presents a significant improvement in the BDS-only solutions in the Eurasia time links. The maximum improvement is up to 84%. For the Galileo-only solution, the improvement ranges from 0.1 to 45.4%.

Third, our approach contains less noise compared to scheme1, both for the single-system model and the multi-GNSS model. The improvement of scheme2 ranges from 36.5 to 92.2% compared with scheme1 for the GPS-only solution. Compared to scheme1, the solutions of scheme2 are improved by 11.8–39.3%, 6.6–43.3%, and 15.0–90.9% for the BDS-only, Galileo-only, and multi-GNSS solutions. For frequency stability, the improvement of scheme2 ranges from 0.2 to 51.6%, from 3 to 80.0%, from 0.2 to 70.8%, and from 0.1 to 51.5% for GPS-only, BDS-only, Galileo-only, and multi-GNSS PPP solutions compared to scheme1 in the Eurasia links. In addition, the performances of scheme2 are improved by 0.3–39.9%, 0.1–52.5%, 0.2–47.8%, and 0.1–40.7% for GPS-only, BDS-only, Galileo-only, and multi-GNSS PPP solutions compared to scheme1 in Asia-Pacific. Note that our approach can also be utilized in real-time multi-GNSS PPP time transfer, which is our next major task.