A Bayesian Kriging Regression Method to Estimate Air Temperature Using Remote Sensing Data
Abstract
:1. Introduction
2. Study Area and Data
2.1. Study Area
2.2. Ground Station Data
2.3. Urban Areas Data
2.4. Land Surface Temperature
3. Methods
3.1. Classical Kriging
3.2. Bayesian Kriging Regression
3.3. Model Evaluation
4. Results and Discussion
4.1. Exploratory Data Analysis
4.2. Cross Validation
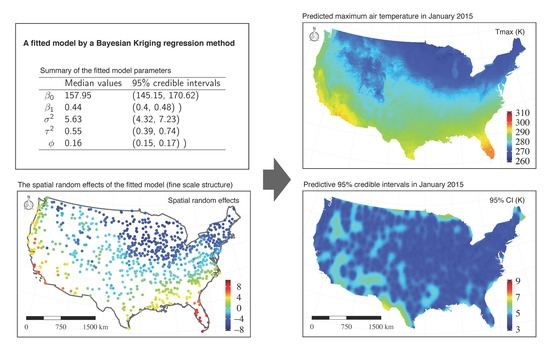
4.3. Model Fitting
4.4. Air Temperature Estimation
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Braga, A.L.F.; Zanobetti, A.; Schwartz, J. The effect of weather on respiratory and cardiovascular deaths in 12 U.S. cities. Environ. Health Perspect. 2002, 110, 859–863. [Google Scholar] [CrossRef] [PubMed]
- Basu, R. Relation between Elevated Ambient Temperature and Mortality: A Review of the Epidemiologic Evidence. Epidemiol. Rev. 2002, 24, 190–202. [Google Scholar] [CrossRef]
- Scovronick, N.; Sera, F.; Acquaotta, F.; Garzena, D.; Fratianni, S.; Wright, C.Y.; Gasparrini, A. The association between ambient temperature and mortality in South Africa: A time-series analysis. Environ. Res. 2018, 161, 229–235. [Google Scholar] [CrossRef] [PubMed]
- Ragettli, M.S.; Vicedo-Cabrera, A.M.; Schindler, C.; Röösli, M. Exploring the association between heat and mortality in Switzerland between 1995 and 2013. Environ. Res. 2017, 158, 703–709. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.K.; Maharani, A.T.; Chang, F.T.; Wang, Y.C. Mortality and morbidity associated with ambient temperatures in Taiwan. Sci. Total Environ. 2019, 651, 210–217. [Google Scholar] [CrossRef]
- Vancutsem, C.; Ceccato, P.; Dinku, T.; Connor, S.J. Evaluation of MODIS land surface temperature data to estimate air temperature in different ecosystems over Africa. Remote Sens. Environ. 2010, 114, 449–465. [Google Scholar] [CrossRef]
- Vogt, J.V.; Viau, A.A.; Paquet, F. Mapping regional air temperature fields using satellite-derived surface skin temperatures. Int. J. Climatol. 1997, 17, 1559–1579. [Google Scholar] [CrossRef]
- Prihodko, L.; Goward, S.N. Estimation of air temperature from remotely sensed surface observations. Remote Sens. Environ. 1997, 60, 335–346. [Google Scholar] [CrossRef]
- Prince, S.; Goetz, S.; Dubayah, R.; Czajkowski, K.; Thawley, M. Inference of surface and air temperature, atmospheric precipitable water and vapor pressure deficit using Advanced Very High-Resolution Radiometer satellite observations: Comparison with field observations. J. Hydrol. 1998, 212–213, 230–249. [Google Scholar] [CrossRef]
- Benali, A.; Carvalho, A.; Nunes, J.; Carvalhais, N.; Santos, A. Estimating air surface temperature in Portugal using MODIS LST data. Remote Sens. Environ. 2012, 124, 108–121. [Google Scholar] [CrossRef]
- Willmott, C.J.; Robeson, S.M. Climatologically aided interpolation (CAI) of terrestrial air temperature. Int. J. Climatol. 1995, 15, 221–229. [Google Scholar] [CrossRef]
- Courault, D.; Monestiez, P. Spatial interpolation of air temperature according to atmospheric circulation patterns in southeast France. Int. J. Climatol. 1999, 19, 365–378. [Google Scholar] [CrossRef]
- Cresswell, M.P.; Morse, A.P.; Thomson, M.C.; Connor, S.J. Estimating surface air temperatures, from Meteosat land surface temperatures, using an empirical solar zenith angle model. Int. J. Remote Sens. 1999, 20, 1125–1132. [Google Scholar] [CrossRef]
- Mostovoy, G.V.; King, R.L.; Reddy, K.R.; Kakani, V.G.; Filippova, M.G. Statistical Estimation of Daily Maximum and Minimum Air Temperatures from MODIS LST Data over the State of Mississippi. GISci. Remote Sens. 2006, 43, 78–110. [Google Scholar] [CrossRef]
- Chen, F.; Liu, Y.; Liu, Q.; Qin, F. A statistical method based on remote sensing for the estimation of air temperature in China. Int. J. Climatol. 2015, 35, 2131–2143. [Google Scholar] [CrossRef]
- Good, E. Daily minimum and maximum surface air temperatures from geostationary satellite data: Satellite min and max air temperatures. J. Geophys. Res. Atmos. 2015, 120, 2306–2324. [Google Scholar] [CrossRef]
- Noi, P.; Kappas, M.; Degener, J. Estimating Daily Maximum and Minimum Land Air Surface Temperature Using MODIS Land Surface Temperature Data and Ground Truth Data in Northern Vietnam. Remote Sens. 2016, 8, 1002. [Google Scholar] [CrossRef]
- Zakšek, K.; Schroedter-Homscheidt, M. Parameterization of air temperature in high temporal and spatial resolution from a combination of the SEVIRI and MODIS instruments. ISPRS J. Photogramm. Remote Sens. 2009, 64, 414–421. [Google Scholar] [CrossRef]
- Yoo, C.; Im, J.; Park, S.; Quackenbush, L.J. Estimation of daily maximum and minimum air temperatures in urban landscapes using MODIS time series satellite data. ISPRS J. Photogramm. Remote Sens. 2018, 137, 149–162. [Google Scholar] [CrossRef]
- Stisen, S.; Sandholt, I.; Nørgaard, A.; Fensholt, R.; Eklundh, L. Estimation of diurnal air temperature using MSG SEVIRI data in West Africa. Remote Sens. Environ. 2007, 110, 262–274. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S. Estimation of daily maximum and minimum air temperature using MODIS land surface temperature products. Remote Sens. Environ. 2013, 130, 62–73. [Google Scholar] [CrossRef]
- Kitsara, G.; Papaioannou, G.; Retalis, A.; Paronis, D.; Kerkides, P. Estimation of air temperature and reference evapotranspiration using MODIS land surface temperature over Greece. Int. J. Remote Sens. 2018, 39, 924–948. [Google Scholar] [CrossRef]
- Sun, Y.J.; Wang, J.F.; Zhang, R.H.; Gillies, R.R.; Xue, Y.; Bo, Y.C. Air temperature retrieval from remote sensing data based on thermodynamics. Theor. Appl. Climatol. 2005, 80, 37–48. [Google Scholar] [CrossRef]
- Moser, G.; De Martino, M.; Serpico, S.B. Estimation of Air Surface Temperature From Remote Sensing Images and Pixelwise Modeling of the Estimation Uncertainty Through Support Vector Machines. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 332–349. [Google Scholar] [CrossRef]
- Meyer, H.; Katurji, M.; Appelhans, T.; Müller, M.; Nauss, T.; Roudier, P.; Zawar-Reza, P. Mapping Daily Air Temperature for Antarctica Based on MODIS LST. Remote Sens. 2016, 8, 732. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, F.; Ye, M.; Che, T.; Zhang, G. Estimating daily air temperatures over the Tibetan Plateau by dynamically integrating MODIS LST data. J. Geophys. Res. Atmos. 2016, 121, 11425–11441. [Google Scholar] [CrossRef]
- Xu, Y.; Knudby, A.; Shen, Y.; Liu, Y. Mapping Monthly Air Temperature in the Tibetan Plateau From MODIS Data Based on Machine Learning Methods. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2018, 11, 345–354. [Google Scholar] [CrossRef]
- Mira, M.; Ninyerola, M.; Batalla, M.; Pesquer, L.; Pons, X. Improving Mean Minimum and Maximum Month-to-Month Air Temperature Surfaces Using Satellite-Derived Land Surface Temperature. Remote Sens. 2017, 9, 1313. [Google Scholar] [CrossRef]
- Zhu, W.; Lű, A.; Jia, S.; Yan, J.; Mahmood, R. Retrievals of all-weather daytime air temperature from MODIS products. Remote Sens. Environ. 2017, 189, 152–163. [Google Scholar] [CrossRef]
- Zhou, W.; Peng, B.; Shi, J.; Wang, T.; Dhital, Y.; Yao, R.; Yu, Y.; Lei, Z.; Zhao, R. Estimating High Resolution Daily Air Temperature Based on Remote Sensing Products and Climate Reanalysis Datasets over Glacierized Basins: A Case Study in the Langtang Valley, Nepal. Remote Sens. 2017, 9, 959. [Google Scholar] [CrossRef]
- Janatian, N.; Sadeghi, M.; Sanaeinejad, S.H.; Bakhshian, E.; Farid, A.; Hasheminia, S.M.; Ghazanfari, S. A statistical framework for estimating air temperature using MODIS land surface temperature data. Int. J. Climatol. 2017, 37, 1181–1194. [Google Scholar] [CrossRef]
- Kloog, I.; Nordio, F.; Lepeule, J.; Padoan, A.; Lee, M.; Auffray, A.; Schwartz, J. Modelling spatio-temporally resolved air temperature across the complex geo-climate area of France using satellite-derived land surface temperature data. Int. J. Climatol. 2017, 37, 296–304. [Google Scholar] [CrossRef]
- Pelta, R.; Chudnovsky, A.A. Spatiotemporal estimation of air temperature patterns at the street level using high resolution satellite imagery. Sci. Total Environ. 2017, 579, 675–684. [Google Scholar] [CrossRef] [PubMed]
- Rosenfeld, A.; Dorman, M.; Schwartz, J.; Novack, V.; Just, A.C.; Kloog, I. Estimating daily minimum, maximum, and mean near surface air temperature using hybrid satellite models across Israel. Environ. Res. 2017, 159, 297–312. [Google Scholar] [CrossRef] [PubMed]
- Wang, M.; He, G.; Zhang, Z.; Wang, G.; Zhang, Z.; Cao, X.; Wu, Z.; Liu, X. Comparison of Spatial Interpolation and Regression Analysis Models for an Estimation of Monthly Near Surface Air Temperature in China. Remote Sens. 2017, 9, 1278. [Google Scholar] [CrossRef]
- Li, X.; Zhou, Y.; Asrar, G.R.; Zhu, Z. Developing a 1 km resolution daily air temperature dataset for urban and surrounding areas in the conterminous United States. Remote Sens. Environ. 2018, 215, 74–84. [Google Scholar] [CrossRef]
- Florio, E.N.; Lele, S.R.; Chi Chang, Y.; Sterner, R.; Glass, G.E. Integrating AVHRR satellite data and NOAA ground observations to predict surface air temperature: A statistical approach. Int. J. Remote Sens. 2004, 25, 2979–2994. [Google Scholar] [CrossRef]
- Oyler, J.W.; Ballantyne, A.; Jencso, K.; Sweet, M.; Running, S.W. Creating a topoclimatic daily air temperature dataset for the conterminous United States using homogenized station data and remotely sensed land skin temperature. Int. J. Climatol. 2015, 35, 2258–2279. [Google Scholar] [CrossRef]
- Parmentier, B.; McGill, B.J.; Wilson, A.M.; Regetz, J.; Jetz, W.; Guralnick, R.; Tuanmu, M.N.; Schildhauer, M. Using multi-timescale methods and satellite-derived land surface temperature for the interpolation of daily maximum air temperature in Oregon. Int. J. Climatol. 2015, 35, 3862–3878. [Google Scholar] [CrossRef]
- Lu, N.; Liang, S.; Huang, G.; Qin, J.; Yao, L.; Wang, D.; Yang, K. Hierarchical Bayesian space-time estimation of monthly maximum and minimum surface air temperature. Remote Sens. Environ. 2018, 211, 48–58. [Google Scholar] [CrossRef]
- Diggle, P.J.; Tawn, J.A.; Moyeed, R.A. Model-based geostatistics. J. R. Stat. Soc. Ser. C Appl. Stat. 2002, 47, 299–350. [Google Scholar] [CrossRef]
- Hengl, T.; Heuvelink, G.B.; Rossiter, D.G. About regression-kriging: From equations to case studies. Comput. Geosci. 2007, 33, 1301–1315. [Google Scholar] [CrossRef]
- Al-Mudhafar, W.J. Bayesian kriging for reproducing reservoir heterogeneity in a tidal depositional environment of a sandstone formation. J. Appl. Geophys. 2019, 160, 84–102. [Google Scholar] [CrossRef]
- Wojciech, M. Kriging Method Optimization for the Process of DTM Creation Based on Huge Data Sets Obtained from MBESs. Geosciences 2018, 8, 433. [Google Scholar] [CrossRef]
- Handcock, M.S.; Stein, M.L. A Bayesian Analysis of Kriging. Technometrics 1993, 35, 403–410. [Google Scholar] [CrossRef]
- Le, N.D.; Zidek, J.V. Statistical Analysis of Environmental Space-Time Processes; Springer: New York, NY, USA, 2006; pp. 119–121. [Google Scholar]
- Banerjee, S.; Carlin, B.P.; Gelfand, A.E. Hierarchical Modeling and Analysis for Spatial Data; Chapman and Hall: Boca Raton, FL, USA, 2014; pp. 12–18. [Google Scholar]
- Menne, M.J.; Durre, I.; Korzeniewski, B.; McNeal, S.; Thomas, K.; Yin, X.; Anthony, S.; Ray, R.; Vose, R.S.; Gleason, B.E.; Houston, T.G. Global Historical Climatology Network-Daily (GHCN-Daily), version 3; NOAA National Climatic Data Center: Asheville, NC, USA, 2012. [Google Scholar]
- Menne, M.J.; Durre, I.; Vose, R.S.; Gleason, B.E.; Houston, T.G. An Overview of the Global Historical Climatology Network-Daily Database. J. Atmos. Ocean. Technol. 2012, 29, 897–910. [Google Scholar] [CrossRef]
- Sobrino, J.A.; Oltra-Carrió, R.; Sòria, G.; Jiménez-Muñoz, J.C.; Franch, B.; Hidalgo, V.; Mattar, C.; Julien, Y.; Cuenca, J.; Romaguera, M.; et al. Evaluation of the surface urban heat island effect in the city of Madrid by thermal remote sensing. Int. J. Remote Sens. 2013, 34, 3177–3192. [Google Scholar] [CrossRef]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Wan, Z.; Hook, S.; Hulley, G. MOD11C3 MODIS/Terra Land Surface Temperature/Emissivity Monthly L3 Global 0.05Deg CMG V006; NASA LP DAAC: Sioux Falls, SD, USA, 2015. [Google Scholar]
- Cressie, N.A.C. Statistics for sPatial Data; Wiley-Interscience: New York, NY, USA, 1993; pp. 105–112. [Google Scholar]
- Finley, A.O.; Banerjee, S.; Gelfand, A.E. spBayes for Large Univariate and Multivariate Point-Referenced Spatio-Temporal Data Models. J. Stat. Softw. 2015, 63. [Google Scholar] [CrossRef]










| Min | Max | Range | Mean | Standard Deviation | |
|---|---|---|---|---|---|
| Tmin | 246.76 | 303.49 | 56.73 | 279.07 | 9.87 |
| Tmax | 260.83 | 316.93 | 56.10 | 291.42 | 10.40 |
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Daytime | 0.95 | 0.96 | 0.92 | 0.73 | 0.59 | 0.76 | 0.66 | 0.79 | 0.76 | 0.91 | 0.91 | 0.96 |
| Nighttime | 0.95 | 0.96 | 0.96 | 0.96 | 0.92 | 0.92 | 0.94 | 0.93 | 0.94 | 0.94 | 0.95 | 0.95 |
| January (Daytime) | January (Nighttime) | May (Daytime) | May (Nighttime) | |
|---|---|---|---|---|
| 157.95 (145.15, 170.62) | 92.81 (77.55, 109.89) | 208.1 (198.22, 217.51) | 100.35 (85.65, 115.97) | |
| 0.44 (0.4, 0.48) | 0.66 (0.59, 0.71) | 0.29 (0.26, 0.32) | 0.65 (0.59, 0.7) | |
| 5.63 (4.32, 7.23) | 3.89 (2.8, 5.32) | 8.24 (6.46, 11.02) | 3.21 (2.36, 4.29) | |
| 0.55 (0.39, 0.74) | 1.22 (1, 1.45) | 0.57 (0.32, 0.79) | 1 (0.83, 1.17) | |
| 0.16 (0.15, 0.17) | 0.15 (0.15, 0.18) | 0.16 (0.15, 0.21) | 0.16 (0.15, 0.21) |
| Month | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Daytime | ||||||||||||
| 157.9 | 173.4 | 178.2 | 193.3 | 208.1 | 193.3 | 193.6 | 190.4 | 187.9 | 162.7 | 149.8 | 173.3 | |
| 0.44 | 0.38 | 0.38 | 0.33 | 0.29 | 0.35 | 0.36 | 0.37 | 0.37 | 0.44 | 0.48 | 0.39 | |
| 5.63 | 7.30 | 5.40 | 7.31 | 8.24 | 7.87 | 7.06 | 5.87 | 4.78 | 3.21 | 3.74 | 5.28 | |
| 0.55 | 0.36 | 0.56 | 0.48 | 0.57 | 0.71 | 0.61 | 0.73 | 0.61 | 0.63 | 0.57 | 0.36 | |
| 0.16 | 0.15 | 0.16 | 0.15 | 0.16 | 0.17 | 0.18 | 0.16 | 0.19 | 0.16 | 0.15 | 0.15 | |
| Nighttime | ||||||||||||
| 92.81 | 107.34 | 56.90 | 54.65 | 100.35 | 59.83 | 52.04 | 32.14 | 27.46 | 44.86 | 69.38 | 97.24 | |
| 0.66 | 0.60 | 0.79 | 0.80 | 0.65 | 0.79 | 0.82 | 0.88 | 0.90 | 0.84 | 0.75 | 0.65 | |
| 3.89 | 5.74 | 1.90 | 2.14 | 3.21 | 2.01 | 1.81 | 1.60 | 1.65 | 1.52 | 2.49 | 3.30 | |
| 1.22 | 1.04 | 1.44 | 1.07 | 1.00 | 0.93 | 0.86 | 1.15 | 1.14 | 1.25 | 1.19 | 1.17 | |
| 0.15 | 0.15 | 0.18 | 0.16 | 0.16 | 0.16 | 0.16 | 0.16 | 0.17 | 0.19 | 0.16 | 0.16 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, Z.; Du, Q. A Bayesian Kriging Regression Method to Estimate Air Temperature Using Remote Sensing Data. Remote Sens. 2019, 11, 767. https://doi.org/10.3390/rs11070767
Zhang Z, Du Q. A Bayesian Kriging Regression Method to Estimate Air Temperature Using Remote Sensing Data. Remote Sensing. 2019; 11(7):767. https://doi.org/10.3390/rs11070767
Chicago/Turabian StyleZhang, Zhenwei, and Qingyun Du. 2019. "A Bayesian Kriging Regression Method to Estimate Air Temperature Using Remote Sensing Data" Remote Sensing 11, no. 7: 767. https://doi.org/10.3390/rs11070767
APA StyleZhang, Z., & Du, Q. (2019). A Bayesian Kriging Regression Method to Estimate Air Temperature Using Remote Sensing Data. Remote Sensing, 11(7), 767. https://doi.org/10.3390/rs11070767