1. Introduction
A unique and popular application of synthetic-aperture radar (SAR) is the monitoring of moving targets [
1,
2,
3,
4,
5,
6], which is a SAR application field of ground moving-target indication (GMTI) [
7,
8,
9,
10,
11,
12]. The main topics of SAR GMTI are the detection of targets and the estimation of their velocities. In a normally focused SAR image in which stationary ground is presumed, it is well known that moving objects are rendered by azimuthal displacement, smearing, and range walking [
1,
2]. The movement of a target during the antenna observation period results in distortion of the Doppler centroid (or Doppler centre frequency) and Doppler rate (or azimuth chirp rate). The distorted Doppler centre frequency contributes to the azimuthal displacement in ordinary SAR images, and the image smearing in the azimuth is caused by the abnormal Doppler rate. The range walk reflects the distance moved by a target in range during the antenna integration time. Thus, there are two issues associated with ground moving targets observed by SAR: the first is to generate an improved SAR image in which moving targets are additionally focused and the position of the target is shifted to the true position through an accurate estimation of the Doppler parameters. Many papers discuss the SAR image signatures of moving targets and propose methods for residual focusing [
12,
13,
14,
15,
16,
17,
18,
19]. On the contrary, SAR GMTI focuses on the analysis of target motion itself rather than image correction. A number of papers propose various methods for SAR GMTI [
8,
20,
21,
22,
23], and multi or at least dual-channel SAR systems are efficient and effective for the detection and velocity estimations of ground moving targets [
8,
10,
11,
12,
17,
24,
25,
26,
27,
28,
29,
30]. However, data of space-borne single-channel SAR systems are currently far more abundant and are easier to access by general users than space-borne multi or dual-channel SAR data. Therefore, it is far more practical to use space-borne single-channel SAR systems for SAR GMTI, although space-borne dual-channel SAR systems have a superior capabilities in terms of the detection rate and the accuracy of the retrieved velocity [
5,
18,
31,
32,
33]. In addition, raw SAR signals of most current space-borne SAR systems are not available to general users because the total size of the raw signal data is too large to transfer to users. Instead of raw SAR signals, single-look complex (SLC) data are fundamental processed SAR data available to general users. This paper focuses on compensating across-track acceleration to improve the accuracy of the along-track velocity of ground moving targets from SLC data obtained by single-channel SAR systems.
Accurate measurement of the instantaneous Doppler phase plays a key role in target-velocity estimation and high-quality image focusing. The instantaneous Doppler phase is a function of relative distance between the SAR antenna and target. The distance between the antenna and target varies not only with antenna path, but also with target motion. The across-track velocity of a given target results in the distortion of the first-order Doppler phase in the azimuth time domain, or equivalently, in a shift in the Doppler centroid in the Doppler frequency domain. It is relatively straightforward to retrieve the across-track velocity by measuring the relative shift in the Doppler centre frequency from the SAR signals. On the contrary, it is more complicated to accurately estimate the along-track velocity from single or multi-channel SAR data. A number of methods have been proposed for the accurate estimation of the Doppler rate, such as methods using matched filter banks [
9,
25,
29], methods based on a joint time-frequency (TF) analysis [
16,
34,
35,
36], and methods utilizing a fractional Fourier transform (FrFT) [
31,
37,
38]. A principal tactic for Doppler rate estimation is to search the optimal Doppler rate that results in the highest compression of the target signal. Minimum entropy is commonly used as a criterion for optimal SAR focusing [
39,
40,
41]. Difficulty arises from the fact that the along-track velocity and across-track acceleration commonly contribute to the second-order Doppler phase or the Doppler rate. Consequently, it is problematic to reconstruct two unknown parameters—the along-track velocity and across-track acceleration—from a single observation, the Doppler rate. Thus, most proposed GMTI methods and literature assume targets moving with constant velocity [
8,
9,
11,
19,
20,
21,
42]. In reality, the across-track acceleration is often not negligible for both on-land vehicles [
10,
43] and vessels at sea [
42]. While the across-track acceleration is not a main parameter of interest for most SAR GMTI applications, it is frequently a major source of error in the estimation of the along-track velocity component. The Doppler phase associated with target acceleration has been theoretically examined by various authors, including those of [
1,
13,
44]. The effects of acceleration on velocity estimation, particularly from dual-channel SAR data, are well discussed in detail in [
10]. Although the effects of acceleration are well known, an effective method of acceleration compensation is yet to be developed. This is mainly because of the fundamental limitation that the separation of across-track velocity from across-track acceleration cannot be achieved with a single parameter, the Doppler rate. Thus far, only one method has been proposed to compensate the effects of target acceleration [
43]. Even the method proposed in [
43], based on a joint time-frequency analysis through the Wigner–Ville distribution, is only effective for dual-channel SAR systems and requires azimuth-uncompressed signals. Thus far, to the authors’ knowledge, there are no papers that propose a method of effectively compensating the across-track acceleration in single-channel SAR SLC data.
This paper proposes a method of compensating the across-track acceleration in single-channel SAR GMTI to improve the estimation accuracy of the along-track velocity of ground moving targets. The method was applied to single-channel SAR SLC data. A unique feature of the proposed method is the estimation of the Doppler phase variation in the Doppler frequency domain instead of time-domain estimation. Combined with the Doppler rate obtained by conventional methods, additional information on the Doppler phase variation in the Doppler frequency domain compensates for the effects of across-track acceleration on the estimation of the along-track velocity in single-channel SAR GMTI. Since there are one-on-one relations between the azimuth time and the Doppler frequency, the variation in Doppler phase with respect to the Doppler frequency directly presents the time-varying Doppler phase, and vice versa. Consequently, the Doppler phase variation in the Doppler frequency domain provides information of time-varying, across-track velocity or average acceleration within a short period. For this purpose, the Doppler phase response of ground moving targets in the Doppler frequency domain is reorganized through the principle of stationary phase, as summarized in
Appendix A. The frequency variation in the Doppler phase can be estimated efficiently by applying a rotational invariance technique (ESPRIT) algorithm, which was originally developed for the estimation of signal parameters in the time domain via rotational invariance techniques [
45,
46]. A modified version of ESPRIT is discussed in [
33], particularly for Doppler frequency estimation from SAR signals. Once the frequency-varying Doppler phase is obtained, particularly around the Doppler centroid, the across-track acceleration can be effectively compensated to improve the estimation accuracy of the along-track velocity component.
The organization of this paper is as follows. In
Section 2, the theoretical background of the proposed method is introduced. The Doppler phase of the azimuth-compressed SAR signal in the Doppler frequency domain is formulated and discussed. The relationship between the target’s motion parameters—velocity and acceleration—and the Doppler phase in the Doppler frequency domain is examined.
Section 3 describes the ground truth data and the TerraSAR-X imagery used in this study. Speed-controlled vehicles were used for the experiment and their velocities were measured using a GPS system.
Section 3 also outlines the processing flow for compensating across-track acceleration to improve the estimation accuracy of the along-track velocity from single-channel SAR SLC images. The results obtained by applying the proposed method to the experimental data are discussed in
Section 4. The along-track velocity estimates before and after the acceleration compensation are compared to the GPS velocities, and the improvements achieved by the proposed method are demonstrated. Limitations of the method are also discussed. A summary of the proposed method and results are presented in the conclusions, followed by
Appendix A, in which the Doppler phase of the azimuth-compressed SAR signals in the Doppler frequency domain is derived.
2. Theoretical Background
The one-dimensional SAR signal can be simplified as
where
is a rectangular function with an azimuth integration time
over a single target. The range
between the antenna and a ground moving target is approximated up to the third order of the azimuth time given by (Sharma, 2006)
where
is the range between the antenna and a target;
the azimuth time or slow time;
the ground range;
the along-track velocity of the antenna;
the azimuth (or along-track) and across-track velocity of the target, respectively;
the azimuth and across-track acceleration of the target, respectively; and
the time derivative of across-track acceleration of the target. Since the target velocity and acceleration terms are very small compared with the range,
, the range
can be further approximated as:
By substituting Equation (3) into Equation (1), the SAR signal is given by
where
and
is the Doppler centre frequency,
the Doppler frequency rate of the Doppler rate, and
the antenna elevation angle. Parameters
,
are defined by Equations (8) and (9), respectively, according to the target motion.
The point target spectrum of the azimuth-compressed SLC signal in the Doppler frequency domain is given by
A detailed derivation of Equation (9) from (8) is described in the
Appendix A.
where
Thus, a compressed point target within the SLC is approximated to a function with a phase of a third-order polynomial in the Doppler frequency domain, as in Equations (10) and (11). Realistic ranges of
,
, and
are summarized in
Table 1, and the Doppler rate
is approximately 5500 Hz/s. Considering the value range of each parameter, the linear, quadratic, and cubic phases are mainly governed by the residual Doppler centre frequency
, residual Doppler rate parameter
, and
, respectively.
Under favourable signal-to-clutter ratios (SCR) in instances larger than 7.7 dB in the sea [
42], it is normally possible to precisely estimate the coefficient of quadratic phase in Equation (12) or the residual Doppler rate
using only a few tens of azimuth samples around the target. There are various methods with which to estimate the quadratic phase term, such as a FrFT-based method in the time domain [
31,
37,
38,
47] or a Doppler-rate filter-bank method [
9,
25,
29]. Both approaches search for a quadratic coefficient until the azimuth signals are optimally compressed. Minimum entropy is a popular criterion for optimal azimuth compression [
39,
40,
41,
48]. The sub-aperture method is also useful [
13,
27]; it does not require the criterion of optimal azimuth compression. However, the accuracy of the sub-aperture method is usually less than those of the FrFT or Doppler-rate, filter-bank-based methods. By applying a suitable method, the quadratic coefficient in Equation (12) can be estimated independently. The detailed discussion of these methods is beyond the scope of this research. The second term in the bracket of Equation (13) is less than the order of 10
−3 and is negligible. As in Equation (8), the residual Doppler rate is usually dominated by the along-track velocity
, provided there is a constant across-track velocity, and consequently, the along-track velocity can be retrieved from the
estimate with the assumption of negligible across-track acceleration. However, as discussed in [
10], it is difficult to separate the along-track velocity
from the across-track acceleration
if the across-track acceleration is significant from single or dual-channel SAR observation. While most applications are interested in the along-track and across-track velocity components
, the non-negligible across-track acceleration frequently causes serious errors in along-track velocity estimation. It might not be possible to separate the
distribution of the
estimate in Equation (8) from that of
without additional observations if the across-track velocity increase is ideally linear with a constant
, as discussed in [
10]. However, the variation in across-track velocity
is not always linear in reality. In this paper, we show that the time variation in
can be measured in the Doppler-frequency domain, and the measured time variation in
is used for compensation of the over or under-estimation of the along-track velocity
, initially calculated from the
estimate with the assumption of a zero across-track acceleration.
Since there is a one-on-one relation between the slow time and the Doppler frequency, it is possible to determine the time variation in
if the frequency variation in
is estimated. Now, let us consider the phase derivative of Equation (12) to yield
The quadratic phase in Equation (12) is the residual Doppler rate caused by the azimuth velocity and across-track acceleration. After estimation of the residual Doppler rate coefficient, the average slope in the Doppler-frequency domain is given by
The linear phase model (Equation (15)) can be easily obtained from
estimated through an optimal residual compression. However, it must be emphasized that the residual Doppler rate parameter
estimated on the basis of optimum azimuth compression represents a global average of the residual Doppler rate over the full azimuth integration time caused by the target motion. If the Doppler phase derivatives in Equation (14) are subtracted from the quadratic frequency phase model (Equation (15)), then the residual Doppler phase derivative is given by
The relationship in Equations (3), (12) and (16) is derived on the basis of an ideal target motion, which assumes that the target moves at a constant across-track velocity with a linear increasing or decreasing rate of over the entire antenna integration time. Then, is a function of the along-track velocity and the across-track acceleration of the target defined by Equation (8). If the behaviour of ground target motion is ideal, as explained, the residual Doppler phase derivative in Equation (16) must be a simple quadratic function. However, the deviation in from the simple model of Equation (15) is significantly higher for most real targets. The deviation mainly accounts for a variation in the Doppler centre frequency with respect to frequency, or equivalently to slow time. Changes in the across-track velocity naturally result in changes in Doppler centre frequencies, as in Equation (5).
The velocity and acceleration model assumed in Equation (2) is a linear velocity variation such that
However, the velocity variation in ground moving targets is often irregular or discontinuous, rather than exhibiting a linear increase or decrease. Instead of a linear variation in velocity with a constant acceleration, here we consider a general velocity variation model such that
where
is the time-varying deviation from mean velocity
. This velocity model accommodates the local or instantaneous variation in target velocity during the antenna integration time, regardless of whether the variation is linear. The core idea behind the proposed approach is that a realistic behaviour of target motion over the full integration time is either non-linear or discontinuously deviated from a mean velocity, rather than exhibiting an ideal linear increase or decrease. In fact, we found that a discontinuous model is frequently more practical for a real ground target, and a typical example is shown in the following section. Then, the across-track acceleration can be considered an accumulated effect of across-track velocity variation. The across-track velocity variations around the broadside time of the antenna-boresight crossing time are particularly interesting. The across-track velocity variation is more easily and precisely estimated as a variation in
in the Doppler frequency domain because the value range of
is far larger than other coefficients in Equation (16). Instead of a direct measurement of acceleration or linear slope of velocity change, here we estimate the time-varying velocity or equivalent at each corresponding frequency. Now, let us introduce a frequency-varying, residual Doppler centre frequency from Equations (5) and (18), defined by
where
and
are normally well satisfied.
A main advantage of the estimation of phase derivatives in the Doppler frequency domain rather than in the time domain is as follows: the peak-to-clutter spectrum ratio around the residual Doppler centre frequency
in the frequency domain is superior to that in the time domain. This can be explained by the fact that the clutter signals seriously affect the target signals according to the distance and the clutter power. This causes a serious limitation in the total number of useful azimuth samples around the target for estimation, and a total observation time that is often too short to estimate the velocity variation or acceleration from azimuth-compression SLC data. On the contrary, the clutter spectrum in the frequency domain spreads over entire frequencies, whereas the target signal is concentrated around the residual Doppler centre frequency
; therefore, a wide bandwidth can be used for the estimation in the Doppler frequency domain. There is a one-on-one relationship between the azimuth time and Doppler frequency
where
represents an absolute value and the azimuth time
is assumed zero at the antenna boresight crossing the target. Consequently, a wide bandwidth for the estimation implies that the total observation time for velocity variation or acceleration increases proportionally to the bandwidth involved in the estimation. In addition, a sample interval for phase differentiation can be easily handled by zero padding before taking a discrete Fourier transform.
By substituting Equation (19) into Equation (16), we have
up to the first order of
. The first term is a constant and is not of interest. The constant term of the Doppler phase derivatives is governed not only by the average across-track velocity
, but also by the position of the target due to the time-shift property of the Fourier transform. Consequently, the constant term is practically meaningless to examine. The residual Doppler centre frequency
is normally determined by phase differentiation in the time domain or a peak of the Doppler spectrum in the frequency domain. The quadratic coefficient of Equation (22) is usually very small, as in
Table 1 and Equation (9), for most targets. However, its contribution is sometimes not negligible when the along-track acceleration is unusually large. In such a case, the asymmetric feature of the compressed azimuth signal is significant; a typical example is shown in the following section. The second term—the residual Doppler centre frequency as a function of frequency—is our main interest. For general ground moving targets, the variation in
is a measure of the time-varying across-track velocity
, as in Equation (20). The behaviour of
around
is particularly informative. Conditions for the estimation of
from Equation (22) are discussed in the next section. Thus, it is possible to retrieve a residual across-track acceleration if the variation in residual Doppler centre frequency
is estimated in the Doppler frequency domain.
Now, let us define an across-track acceleration equivalent as follows.
where
is a certain bandwidth for the estimation around the residual Doppler centre frequency, which can be determined by considering the noise level of the Doppler spectra. The acceleration defined in Equation (23) is an average acceleration over the period of
centred at
. The time length
can be extended to a full antenna integration time but is practically limited by considering the SCR of each target. The difference in Doppler centre frequency variation in Equation (23) can be measured from Equation (22) such that
Since
, the second term of Equation (24) is very small compared with the first term, and is negligible for most cases, unless
, or equivalently, the along-track acceleration
, is very large. However, a target with a very large
is sometimes dominant in the Doppler phase derivatives of Equation (22). In such a case, the Doppler phase derivatives
and the model from the residual Doppler rate
in Equation (16) have a low correlation, and a different tactic is required. In the practical implementation of Equation (24), it is better to apply the method of least squares over the bandwidth of
to determine the variation in residual Doppler centre frequency. Although the acceleration estimated by Equation (23) may not be sufficiently precise to account for actual across-track acceleration, it is very useful to compensate for the over or under-estimated along-track velocity
. From Equation (8), the acceleration-compensated along-track velocity is computed by
To perform the phase derivations
of Equation (14) in the Doppler frequency domain, it is effective to apply the ESPRIT method [
33,
45,
46] with a certain length of sliding window to the Fourier-transformed SAR SLC data. Various lengths of sliding window were tested, and a quarter of a full-length Doppler spectrum,
N/4, was the most effective with a Hamming window function. The interpretation of Equation (14) is similar to joint time-frequency analysis because there is a one-to-one relation between the Doppler frequency and the azimuth time for a given target. However, there is a difference in the dependent variable between the joint time-frequency analysis and Equation (14). The joint time-frequency analysis is carried out in the time domain, and consequently, the resulting dependent variable is a Doppler frequency according to the azimuth time. However, Equation (14) has phase derivatives in the Doppler frequency domain, and consequently, the dependent variable is a Doppler phase derivative in the frequency domain according to Doppler frequency, or equivalently, the azimuth time. Thus, Equation (14) presents the variation in residual Doppler centre frequency according to the azimuth time; the changing rate and pattern for a given bandwidth are meaningful, whereas the absolute value is meaningless.
A flat earth is assumed for the derivation of Equation (25). However, it is mandatory for a space-borne SAR system to apply an orbital configuration on computation of the velocity variation from the variation in Doppler centre frequency. This is achieved by applying the configuration explained in [
49]. Correction for an orbital SAR system was applied to all results in this study.
4. Application Results and Discussion
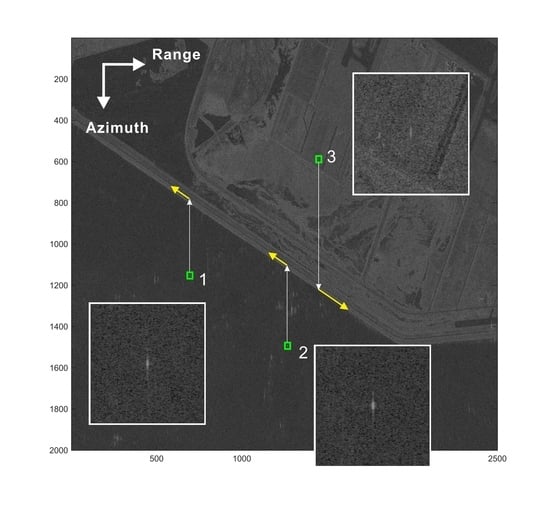
The first example is of a speed-controlled, on-land vehicle with a typical behaviour of velocity variation.
Figure 3 presents the results from the speed-controlled vehicle 1 in
Figure 1, whose velocity was measured by an onboard GPS system. In
Figure 3a, the solid black line represents the Doppler spectrum, and its Doppler centre frequency was determined by the mass centre of the Doppler spectrum and by the ESPRIT method [
45,
46] in the time domain. The Doppler phase derivatives in the Doppler frequency domain are displayed with a blue line in
Figure 3a, which also shows the variation pattern around the Doppler centre frequency. The solid red line in
Figure 3a was obtained by the residual Doppler rate estimated in the time domain and has a squared correlation coefficient of 0.97 with the Doppler phase derivatives.
In fact, the proposed method is only valid with a high correlation between the residual Doppler rate model and the Doppler phase derivatives, and here we set 0.9 as the lower boundary for a valid squared correlation coefficient. Note that the phase derivatives deviate from the model straight line around the Doppler centre frequency, and the deviation contributes to the across-track acceleration. After subtracting the residual Doppler rate model (red solid line) from the Doppler phase derivatives (blue solid line), as in Equation (21), and multiplying by the residual
, the residual is given as
Figure 3b. The velocity variation around the beam centre crossing time, or equivalently, around the Doppler centre frequency, can be estimated from the average slope, as in
Figure 3b. In this case, a bandwidth of 1717 Hz, or equivalently, 0.316 s around the Doppler centre frequency, was used for estimation of the across-track acceleration. The estimated across-track acceleration was 0.0681 m/s
2, from which the along-track velocity was corrected from −8.54 to −6.89 m/s. The GPS-measured along-track velocity was −6.61 m/s (−23.8 km/h), and the absolute error was reduced by 1.65 m/s (5.94 km/h), from 1.93 m/s to 0.28 m/s, through the proposed acceleration compensation.
A simulation was carried out to confirm the estimation, as summarized in
Figure 4. From the estimated acceleration of 0.681 m/s
2 and the shape of the residual velocity variation (blue solid line in
Figure 3), we assumed a velocity variation as a step function as in
Figure 4a, rather than a linear model. The velocity variation model in
Figure 4a presents a velocity jump of 0.03 m/s over 0.45 s, from −13.618 to −13.648 m/s.
All parameters for the simulation were adopted from the actual data from header information or estimated data from the SLC data used: the system and residual Doppler rate were 5438.1 and −11.2 Hz/s, respectively, with a PRF of 3815.5 Hz. Raw signals were simulated first, and then a general azimuth compression was applied to simulate the SLC data. As shown in
Figure 4b, the Doppler phase derivatives obtained from the velocity jump model (red dashed line) match very well with that of the actual SAR data (blue solid line) with a squared correlation coefficient of 0.999. On the contrary, linear velocity increase or decrease models simply change the slope of the straight line, which does not account for the actual velocity variation pattern in
Figure 4b.
The second example summarized in
Figure 5 is also a frequently observed typical case of vehicles on land. The vehicle denoted “3” (hereafter referred to as vehicle 3) showed a low SCR of 9.7 dB. Under low-SCR conditions, the signals from a given target are seriously distorted by surrounding clutter. Compared with vehicles 1 and 2, which were imaged on the water surface, the SCR of vehicle 3 was only 9.7 dB, as in
Table 2. Since the estimation of the Doppler rate in time or Doppler frequency domain is the average value over the antenna integration time, it often leads to an incorrect value when the signals are distorted by those from neighbouring strong scatterers or clutter. As in
Figure 5a, the Doppler spectrum (black solid line) was seriously corrupted by clutter, and its antenna beam pattern was largely distorted at high Doppler frequencies. However, the Doppler spectrum is well preserved around the Doppler centre frequency (black dashed line), and it is better to estimate the along-track velocity only around the centre frequency (i.e., at antenna boresight crossing time) rather than over a full bandwidth (or full antenna integration time). The initial estimate of the Doppler rate (red solid line in
Figure 3a) was significantly overestimated, and consequently resulted in a large error in along-track velocity. The Doppler phase derivative (blue solid line) significantly deviated from the Doppler rate model, but maintained a high correlation of 0.99 between the model and the actual Doppler phase derivatives over 45% of the full bandwidth around the Doppler centre frequency, as seen in
Figure 5a. The estimated across-track acceleration was −0.155 m/s
2. The estimation error of the along-track velocity significantly reduced from 5.27 to 1.49 m/s by compensating the cross-track acceleration as in
Table 2. This example demonstrates a main advantage of the proposed method such that the estimation using limited bandwidth around the Doppler centre frequency provides an improved accuracy compared to estimation over the full antenna integration time.
The improvement by adopting the proposed method is obvious, as summarized by the two resulting velocity vectors in
Figure 6. The ground truth along-track velocity was 10.11 m/s. While the initial estimate of the along-track velocity was 15.38 m/s without acceleration compensation, the along-track velocity was reduced to 11.60 m/s after applying the proposed acceleration compensation. Through the acceleration compensation, the total velocity reduced from 25.2 m/s (90.8 km/h) to 23.1 m/s (83.2 km/h). With correction of the along-track velocity, the heading direction was adjusted by 7.5° and became parallel to the road. An improved heading direction provides very useful information for the interpretation of ground moving targets when compared with roads or other ground structures.
The third example in
Figure 7 is for the case of vehicles with cubic or higher-order motion. The vehicle denoted “2” (hereafter referred to as vehicle 2) in
Figure 2 was one of the speed-controlled trucks for the field experiment. The speed and heading direction were designed to be identical to those of vehicle 1. However, the vehicle apparently moved with slightly different behaviour. While the Doppler spectrum of vehicle 3 (
Figure 7a) is very similar to that of vehicle 1 (
Figure 3a), the shape of the phase derivatives is not linear, as in
Figure 7a. Consequently, the residual Doppler rate model (blue solid line) based on Equation (14) does not accurately account for the actual Doppler phase derivatives (red solid line) with a very low squared correlation coefficient of 0.11. Since the squared correlation coefficient is far lower than 0.9, the proposed method is not effective for the estimation of across-track acceleration.
The proposed method is only valid if the squared correlation coefficient between the Doppler rate model and the actual Doppler phase derivatives is sufficiently high; for instance, it was 0.9 in this study, over the bandwidth of estimation involved. For vehicle 2, cubic-phase motion was apparently significant, as seen in
Figure 2. In such a case, the Doppler phase derivative is used for analysis of a cubic-phase motion and residual compression instead of estimating the across-track acceleration. The Doppler phase derivatives in
Figure 3a imply that the contribution of the last term in (21)
is significant. Recall that
is a function of the along-track acceleration and time derivative of the across-track acceleration, as defined in Equation (9), which are not the main features of interest for this study or most users. However, this parameter—if not small—is useful for residual compression; a best-fitted cubic-phase model was obtained using 50% of the full bandwidth around the Doppler centre frequency, as in
Figure 3b.
Figure 8 displays the original and residual compressed signals. An optimal quadratic phase was first estimated on the basis of the minimum entropy criterion, and then a residual compressed signal (blue solid line) was obtained by removing the quadratic phase from the original SLC signal (black solid line). This residual compression is a general residual compression process and results in a slightly further compressed signal of vehicle 2, as in
Figure 8. Entropy is a popular criterion for evaluating residual focusing quality of a point target, and is defined in [
39,
40].
where
and
is a two-dimensional summation of the power image, and
an SLC data at the
nth azimuth sample and
mth range bin within a sub-scene.
The values of the original model and the model with the removed quadratic-phase signals in
Figure 8 are 2.646 and 2.627, respectively, which implies that the residual compression by the optimal quadratic-phase model is not large. On the contrary, the entropy significantly reduced to 2.148 after the residual compression by the cubic-phase model, as seen in
Figure 8. The original SLC signals rendered two peaks around the centre of the target. The residual compression by the quadratic-phase model slightly reduced the left peak, while increasing the right peak; however, it remains unclear whether there are two peaks or one peak with asymmetric side-lobes. After the residual compression by the cubic-phase model, it is clear that the target consists of one point target in the shape of typical sinc function. The results strongly support that the along-track acceleration was dominant at moment of SAR observation, while the across-track acceleration was not significant. Since the residual compression was done by a cubic-phase model, there exists asymmetry of the second and higher-order side-lobes, as discussed in [
7].
In summary, the motion of ground vehicles or other moving targets in reality is complicated. A simple model of continuous and linear acceleration often cannot account for the actual motion of the ground moving target; however, accurate measurement of acceleration is usually neither easy nor a main interest of most SAR applications. Moreover, most onboard GPS systems are not suitable for measuring acceleration occurring over less than one second. Instead, it is necessary for most SAR ground-moving target applications to measure velocity as accurately as possible. Appropriate across-track acceleration compensation for the correction of the along-track velocity component is a major concern of this study. The proposed method is effective and efficient for the correction of along-track velocity as a consequence of the precise estimation of across-track acceleration from single-channel space-borne SAR SLC data.