Coastline Fractal Dimension of Mainland, Island, and Estuaries Using Multi-temporal Landsat Remote Sensing Data from 1978 to 2018: A Case Study of the Pearl River Estuary Area

Abstract

The Pearl River Estuary Area was selected for this study. For the past 40 years, it has been one of the most complex coasts in China, yet few studies have analyzed the complexity and variations of the area’s different coastlines. In this investigation, the coastlines of the Pearl River Estuary Area were extracted from multi-temporal Landsat remote sensing data from 1978, 1988, 1997, 2008, and 2018. The coastline of this area was classified into mainland, island, and estuarine. To obtain more detailed results of the mainland and island, we regarded this area as the main body, rezoned into different parts. The box-counting dimension was applied to compute the bidimensional (2D) fractal dimension. Coastline length and the fractal dimension of different types of coastline and different parts of the main body were calculated and compared. The fractal dimension of the Pearl River Estuary Area was found to have increased significantly, from 1.228 to 1.263, and coastline length also increased during the study period. The island and mainland showed the most complex coastlines, while estuaries showed the least complexity during the past forty years. A positive correlation was found between length and 2D-fractal dimension in some parts of the study area. Land reclamation had the strongest influence on fractal dimension variations.

1. Introduction

The coastal area is one of the most significant elements of Earth’s ecosystems, providing habitats for humans and other creatures [1]. Serving as the boundary between land and sea, the coastline is influenced by natural and anthropogenic factors [2,3]. It is essential to understand the length variations and irregularities of coastlines, as reflected by fractal dimension. Since the implementation of the Reform and Opening-up policy in China in 1978, the coastal area of China has shown dramatic variations due to the significant requirement of land for economic progress [4]. For example, substantial changes appeared in the Pearl River Delta in the southeast of China, which is the pioneer of reformation and development [5,6,7]. With its unique location, frequent interactions between sea and land have occurred in the Pearl River Delta area which have led to significant coastline variations from the natural. In addition to natural influences, anthropogenic activities have taken place in this area over the past 40 years, with the aim of boosting the construction of facilities [8]. The reclamation of land towards the sea has occurred in the coastal area to create more land resources, not only in this particular area, but also in all of China [9]. A detailed understanding of coastlines and their variations in China can provide useful information for coastal management, coastal zoning planning, and coastal preservation.

In the past, scientists analyzed coastlines around the world using remote sensing. Cui et al. (2011) analyzed coastline variations of the Yellow River Estuary using a Landsat dataset and applied a threshold segmentation method to extract the coastline [10]. Li and Gong (2016) analyzed coastline variations in western Florida over the past 30 years using a Landsat dataset [11]. They extracted the coastline using a subpixel method. Sagar et al. (2017) have analyzed Australian coastline dynamics during the past 28 years using a Landsat dataset to extract the coastline [12]. They applied the normalized difference water index to extract the coastline from remote sensing imagery. These studies indicate that remote sensing plays a significant role in monitoring the spatiotemporal variations in coastlines.

Length is an important element of the coastline, and has been widely studied in the past, and fractal dimension (FD) is another useful and direct way to understand geometric coastline complexity and variations. This theory was first proposed by Mandelbrot in 1967 to describe the exact realistic length of the coastline of Britain [13]. This method has been widely used in many other areas, for example, to evaluate the condition of clouds, mountains, grain boundary, coal, river drainage networks, active faults, plutonic bodies, and other related disciplines [14,15,16,17,18,19,20,21]. Using Mandelbrot’s research on the coastline dimension, many scientists have calculated the FD of coastlines all around the world [22,23,24,25,26].

The divider, spectrum, and box-counting methods are the most common methods used to compute FD [14]. In 1967, Mandelbrot introduced the divider method as a way to calculate FD [13]. The fundamental concept of the divider method is to measure the coastline by different lengths of rulers. The change of length will lead to a different length of coastline. The spectrum method was presented by Pentland in 1984, who developed a way to process the whole image using the Fourier power spectrum and then calculated the FD by involving the Brownian function [27]. Gagnepain and Roques-Carmes first introduced the box-counting method into FD calculations in 1986. This method uses squares with different side lengths to cover the objects. When changing the side length, the number of squares covering the objects will also change [28].

In the past, scientists have used FD to analyze coastal conditions worldwide. For example, Mandelbrot (1967) calculated the FD of the coast and land frontier around the world [13]. Later, Carr and Benzer (1991) compared the divider and spectrum methods and calculated the FD of several coasts in Australia, the USA, and Britain [29]. In 1998, Jiang and Plotnick analyzed the FD of the coastline of the United States using the divider method. Further discussion, including the relationship between FD and topographic complexity were provided, as well as other related topics such as species diversity and coastline complexity [30].

Applying fractal theory to the coastal zone in China has been a focus of many scientists. Zhu (2004) calculated the FD of Chinese coastlines using the box-counting method, and pointed out a limitation of the divider method because it required all objects to be connected, whereas the box-counting did not [23]. In 2014, Xu et al. analyzed coastline variations in northern China from 2000 to 2012 using both length and FD. They calculated the FD using the box-counting method and found that the FD of the study area increased smoothly with length of coastlines [24]. Recently, Li et al. (2018) analyzed changes in the coastline FD of the Zhejiang Province over the past twenty-five years. They calculated FD by also using the box-counting method, and found that the FD in Zhejiang Province displayed retreat after 2000 [22].

Although scientists have calculated coastline FD to analyze the complexity of the coastal zone in the past, they cannot provide information on the differences among the mainland, islands, and estuarine coastlines. Past related research of the Pearl River Estuary only calculated the FD of the whole study area, without any comparison among estuaries or among mainland, islands, and estuaries. Furthermore, previous studies did not compare different parts of the Pearl River Estuary.

Fractal dimension indicates the complexity of coastlines and provides details of the coastal area. It is, therefore, useful for analyzing the Pearl River Estuary Area (PREA), one of the most complex coasts in China. Furthermore, related geographic and environmental influences have previously been rarely discussed. It is well recognized that meandering coastlines that cover the PREA include natural and artificial elements. After 1978, artificial coastlines increased dramatically to create more land resources for infrastructure. The changes in coastlines are likely to lead to changes in FD. It can be assumed that the FD is different among the coastlines of mainland, islands, and estuaries. There are eight estuaries in the PREA; it is necessary to understand the differences of FD among them.

In order to provide a comprehensive analysis, this study aimed to calculate the FD of the Pearl Estuary Area from 1978 to 2018. The aims of this study are:

• To classify the coastline of the Pearl River Estuary as estuarine, mainland, and island coastlines, and then calculate the coastline length and FD of each type of coastline.
• To analyze the reasons for the length increases and differences between different types of coastlines and discuss comparisons between estuaries and Parts I–IV of the main body.
• To analyze the reasons for variations in FD throughout the 40-year time period and how different circumstances influenced the FD.
• To discuss how natural and anthropogenic factors impacted on FD and coastline length, and compare the FD of the study site with other coastal areas of China.

2. Materials and Methods

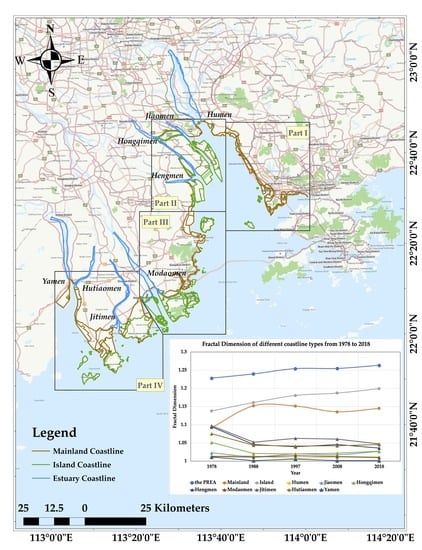
2.1. Study Area

The PREA is located in the southeast of China (Figure 1). It is the second largest river system in China, the largest estuary in Southern China, and one of the most complex fluvial networks in the world [5,31]. The annual mean temperature ranges from 14 to 22 °C [32] and the annual mean precipitation is 1470 mm [33]. The dry season is from September to March in the next year, and the wet season is from April to August [34]. During the wet season, the precipitation accounts for 72–88% of the total annual rainfall [32]. The average water depth of the study site is 30 m [9].

Weak tidal conditions and low sediment concentrations are found in this area [34]. The tidal condition of the PREA is mixed semidiurnal [35]. The average tidal range is from 86 cm to 163 cm [9]. Previous observational data suggests that the significant wave height of the PREA is less than 0.5 m in summer [35]. Some scientists considered the tidal condition of the PREA to be weak [34], and low sediment concentrations were found in this area [34]. Recently, the mean annual sediment decreased to 3.04 × 10⁷ tons, with nearly 95% of the sediment being transported during the wet season [35]. Coarse sediment was the most dominant near estuaries and channels [35].

The unique geographic characteristics of the PREA include eight estuaries, namely Humen, Jiaomen, Hongqimen, Hengmen, Modaomen, Jitimen, Hutiaomen, and Yamen (Figure 1). The gross domestic product in this area has soared since 1978 due to the Reform and Opening-up policy [8,36]. More than 8636 reservoirs had been established by the late 1990s [33].

The PREA encompasses an extremely large area, so for a better understanding, the mainland and island were rezoned into smaller parts. The mainland coastline and island coastline of the PREA were regarded as the main body of the entire PREA in this study. The area was divided into four parts: Part I, Part II, Part III, and Part IV (Figure 1), and each part consisted of mainland and island coastline. Due to their unique geological positions, different parts show different coastline variations.

The main body of the PREA was divided into Parts I–IV, based on their unique locations. The mutual characteristic among these parts is human activities that have facilitated coastline change during the study period. Part I is located in the east of the PREA and includes the rapid development of Shenzhen during the past forty years. In this part, land reclamation focused on the mainland area and islands, showing a smooth increase throughout. This part does not contain estuaries. Part II shows significant past changes of island reclamation. This part exhibited the most significant island variations compared with the other three parts. Similar to Part II, the islands of Part III also show significant changes. This part contains the Modaomen and Macau Special Administrative Region. The coastline variations of Part IV differ from the other parts. Land reclamation has filled the area between the mainland and islands since 2008; therefore, the FD of this area shows different results to the other parts.

2.2. Remote Sensing Dataset

In this study, Landsat remote sensing data were used to extract the coastlines of the study site from 1978 to 2018 (

Table 1. Remote sensing dataset used in this study.

Date (yy/mm/dd)	Spacecraft Identifier/Sensor Identifier	WRS Path-Row	Cloud Cover (%)	Spatial Resolution (m)	Real-Time Tidal Level (cm)	Tidal Difference (cm)
1978/11/02	Landsat 2 MSS	122-44	0	80	208	-
1978/11/02	Landsat 2 MSS	122-45	1	80	208	-
1988/11/24	Landsat 5 TM	122-44	9	30	174	-34
1988/11/24	Landsat 5 TM	122-45	3	30	174	-34
1997/08/29	Landsat 5 TM	122-44	1	30	268	50
1997/08/29	Landsat 5 TM	122-45	3	30	268	50
2008/12/09	Landsat 7 ETM+	122-44	0	30	195	-13
2008/12/09	Landsat 7 ETM+	122-45	0	30	195	-13
2018/02/12	Landsat 8 OLI_TIRS	122-44	7.55	30	190	-18
2018/02/12	Landsat 8 OLI_TIRS	122-45	9.09	30	190	-18

). All datasets were downloaded from the Geospatial Data Cloud (https://www.gsclound.cn/) and the USGS (https://www.usgs.gov/). Data with nearly no cloud cover in the study site were required for this study, as well as dry season time period data. A digital elevation model of Guangdong Province with a spatial resolution of 30 m was downloaded from: http://www.tuxingis.com/. All tidal data were collected from the South China Branch of the State Oceanic Administration (Table 1).

In this study, tidal influence was considered, and according to data collected from South China Branch of the State Oceanic Administration, the tide height ranges from 190 cm to 200 cm. The average slope for the study area, calculated using ArcGIS, 10.3 is 5.39%. The error of the Landsat images would be less than 30 m (spatial resolution) if the tidal difference value is less than 161.7 cm [37], hence, the tidal influence data we used in this study were less than one pixel.

The flow chart of the entire process is shown in Figure 2. The coastline was extracted using automatic and visual interpretation in ArcGIS 10.3 and MATLAB 2014a. The box-counting method was applied via ArcGIS to calculate the 2D-FD of the different coastlines.

2.3. Coastline Extraction and Accuracy Assessment

For the coastline extraction, an automatic and visual interpretation method was used with the Landsat dataset (Table 1). Image analysis software (ENVI) was applied for image pre-processing, including radiometric calibration, FLAASH atmospheric correction, and stripe repair for Landsat 7 ETM+. Canny Edge Detection in MATLAB was used to extract the coastline and examine by visual interpretation in ArcGIS 10.3. The coastline length was calculated in ArcGIS 10.3 using the Calculate Geometry tool.

A precision test was applied to evaluate the accuracy of the extracted coastline, and an image was obtained from Google Earth™ Pro. To maintain a consistent time, the Landsat 8 OLI_TIRS data were collected on February 12, 2018, and the Google Earth image was collected on January 18, 2018. Eighty-six ground control points (GCPs) were selected from the Google Earth image (Figure 3). The distances between each GCP and the corresponding point on Landsat were calculated (Figure 3c) [9]. The average error of all GCPs and the corresponding points on Landsat, the standard deviation, and the root-mean-square error of these points were calculated using the distances obtained between each GCP and corresponding point. Using these data and the theoretical maximum allowable error proposed by Hou et al (2016), the accuracy of the coastline extraction was obtained [9]. The results of the precision test are shown in

Table 2. Result of precision test (SD: standard deviation; RMSE: root-mean-square error; TMAE: theoretical maximum allowable error).

Group	Error (m)	Group	Error (m)	Group	Error (m)	Group	Error (m)	Group	Error (m)	Average Error (m)	SD (m)	RMSE (m)	TMAE (m)
1	27.24	21	29.60	41	22.52	61	9.31	81	4.71	16.21	11.99	20.12	28.28
2	5.31	22	4.46	42	26.00	62	16.73	82	1.30
3	14.98	23	12.69	43	31.25	63	0.99	83	20.59
4	18.81	24	1.03	44	17.41	64	36.58	84	37.49
5	10.03	25	25.50	45	26.35	65	0.83	85	14.72
6	7.99	26	24.81	46	17.13	66	38.65	86	22.18
7	7.70	27	5.62	47	14.27	67	39.86
8	9.67	28	18.43	48	5.44	68	29.99
9	20.16	29	10.62	49	4.83	69	33.80
10	10.72	30	7.83	50	31.61	70	3.59
11	4.57	31	23.82	51	3.47	71	6.10
12	15.25	32	23.67	52	9.84	72	5.24
13	8.96	33	4.59	53	17.74	73	39.51
14	3.93	34	12.34	54	9.67	74	6.22
15	22.34	35	20.72	55	27.22	75	11.47
16	9.73	36	20.37	56	5.64	76	18.48
17	4.22	37	5.08	57	5.45	77	10.01
18	1.66	38	8.35	58	14.25	78	35.66
19	31.58	39	3.46	59	32.66	79	0.99
20	13.80	40	59.00	60	20.89	80	35.07

.

The coastline was classified in ArcGIS 10.3 by different locations including the estuary, mainland, and island (Figure 1) by visual interpretation. The estuary coastline represents approximately eight outlets, and usually extends from the beginning of the junction of the tributaries to the end of the outlet to the sea. The mainland coastline incorporates the boundary between the mainland and sea, while the island coastline is a terrestrial and marine boundary of islands (Figure 1). It is apparent that the island coastline is the boundary between the island and the sea (Figure 1). In this study, the mainland and island coastline of the PREA were regarded as the main body of the entire PREA. This area was divided into four parts, namely Part I, Part II, Part III, and Part IV (Figure 1). Each part comprised mainland and island coastline. The FD of the different coastlines were then calculated in ArcGIS 10.3.

2.4. Fractal Dimension Calculation

The box-counting method was selected for the following reasons. From previous studies, several researchers commented that the box-counting method exhibited inconsistency whereby the box size and different scales also led to different FD [14,38]. The level of confidence of this method reached 99.9%, more than 99% from previous reports [39,40]. Compared with other methods, the box-counting method could provide the FD of discontinuous coastlines [41], which was the main reason it was selected for this study. In addition, research has found that different FD values would be produced when using different methods [29,41]. For example, the divider method obtained a larger value compared to the box-counting method in the same study area; therefore, the results from different methods cannot compare with each other directly. The result obtained from the box-counting method can compare with other studies calculated using the same method, therefore providing a more comprehensive analysis. Furthermore, Li et al. proposed that the box-counting method is easy to conduct using related automatic software [22].

The box-counting method differs from the divider method using different size of squares to cover the same coastline. When the size of square changed, the number of used squares would change. Equation (1) shows the mathematical process for calculating the fractal dimension with a series of square sizes. N represents the number of squares and r represents the size of the squares. The fractal dimension of coastline obtained is a value between 1 and 2. A larger value represents a more complex coastline.

The coastline length would not change when squares of different sizes are applied. Figure 4 shows a number of different square sizes to cover the same coastline, with the left using 1200 m squares and the right using 2700 m squares. The coastline length of (a) and (b) are the same, being 108.28 km; however, the change of grid size led to a different number of grids required.

$$FD=-\underset{r\to 0}{\lim }\frac{\log N\left(r\right)}{\log r}$$

(1)

Further analysis included a FD comparison among different coastline types, different locations (Part I, Part II, Part III, and Part IV), and different outlets were compared with previous studies. The relationship between coastline length and FD were also analyzed.

Different box sizes were involved based on different spatial resolutions, and different coastlines contained different lengths. For the entire PREA, mainland, and island, squares with 400 m, 800 m, 3200 m, 6400 m, and 12,800 m were for Landsat MSS, and squares with 300 m, 900 m, 2400 m, 4800 m, and 12,000 m were for the 30 m spatial resolution. For the four regions of the main part (Parts I–IV), squares with 240 m, 400 m, 1600 m, 3200 m, and 6400 m were for the 1978 coastline, and squares with 210 m, 300 m, 1200 m, 2700 m, and 6000 m were for the 30 m spatial resolution. For estuaries, squares with 80 m, 160 m, 320 m, 400 m, and 640 m were for the 1978 coastline, and squares with 30 m, 120 m, 240 m, 300 m, and 480 m comprised the remainder of the coastline.

When the counting of the number of squares was completed, a linear regression on square quantity log(N) and square size log(r) was conducted in Excel, as well as the R² (coefficient of determination). A further analysis of the combined FD and coastline length was also conducted. A linear regression between the coastline length and FD was calculated, and the R² (coefficient of correlation) showed the relationship between these two parameters.

3. Results

In this section, the length and 2D-fractal dimension of different types of coastline and different parts of the main body are described.

3.1. Result of Accuracy Assessment

The result of the precision test is shown in Table 2. We defined group data as each GCPs from Google Earth and the corresponding points on the Landsat dataset. Table 2 shows the average error as 16.21 m, which is smaller than the theoretical maximum allowable error of 28.28 m put forward by Hou et al. in 2016 [42]. Therefore, the coastline extracted in this study meets the accuracy standard.

3.2. Length of Coastlines

Table 3. The length of coastlines depended on different types from 1978 to 2018 (unit: km).

Different Types		1978	1988	1997	2008	2018
The PREA		1133.43	1208.55	1321.16	1312.9	1349.73
Mainland		371.71	451.14	488.57	512.45	510.36
Islands		434.82	426.93	501.52	467.42	502.17
Estuaries	Humen	71.32	73.68	73.82	74.87	76.05
	Jiaomen	23.83	23.09	23.76	23.66	24.24
	Hongqimen	74.22	74.14	74.99	74.87	75.51
	Hengmen	22.81	22.25	22.76	26.29	26.25
	Modaomen	60.62	69.38	70.82	71.09	71.32
	Jitimen	69.45	69.45	67.94	69.72	73.05
	Hutiaomen	40.01	40.67	41.23	41.05	41.04
	Yamen	58.60	58.73	58.71	58.99	59.27

and

Table 4. Coastline length of the PREA including all coastline types from 1978 to 2018 (unit: km).

Locations	Types	1978	1988	1997	2008	2018
Part I	Total length	97.38	104.83	120.28	125.23	136.38
	Mainland	77.62	84.22	99.14	102.21	108.28
	Island	19.76	20.61	21.14	23.02	28.10
Part II	Total length	240.13	269.84	309.87	315.11	334.35
	Mainland	95.88	97.44	104.27	100.63	103.53
	Island	144.25	172.40	205.60	214.48	230.82
Part III	Total length	213.71	235.69	278.35	269.41	277.85
	Mainland	85.05	95.73	98.52	97.11	94.68
	Island	128.65	139.95	179.83	172.30	183.16
Part IV	Total length	239.00	230.99	246.20	240.42	234.54
	Mainland	96.19	142.51	150.81	181.52	173.97
	Island	142.81	88.48	95.29	58.90	60.58

list the length of different types of coastlines, including the entire study site, mainland, islands, eight estuaries, and four parts. For the four parts, the total length of coastline length represented the sum of the mainland coastline length and the island coastline length of the respective part (Table 4).

Table 3 and Table 4 demonstrate that the coastline length of the PREA increased from 1133.43 km in 1978 to 1349.73 km in 2018. The mainland, island, and coastlines of the estuaries showed an increasing trend (Table 2). The mainland coastlines had an increased length, from 371.71 km in 1978 to 510.36 km in 2018. This represents the most rapid growth rate. The length of the island placed in the second sector changed its rate and improved by almost 100 km during the study period. Unlike the significant growth speed of these two types, the estuary coastlines demonstrated a stable trend with a smooth increase of 1–10 km among the eight estuaries (Table 3). Among the eight estuaries, Modaomen showed the most significant variations, with an increase of nearly 10 km during the study period. The Jiaomen, Hongqimen, Hutiaomen, and Yamen estuaries experienced a slight increase of approximately 1 km. The Humen, Hengmen, and Jitimen estuaries increased by nearly 5 km. Compared with the mainland and island coastlines, the estuaries of the PREA remained stable.

For Parts I–IV, different parts showed different trends. The mainland and island of Part I increased over the past four decades, with the mainland increasing by nearly 30 km and the island increasing by nearly 10 km. Part II showed significantly increased island coastlines, advancing nearly 100 km and a slight increase of mainland coastline during the time period. Similar to Part II, the island coastline increased sharply during the time period, increasing approximately 60 km, while the mainland coastline grew gradually from 85.05 km initially to 94.68 km at the end of the forty years. Part IV demonstrated coastline variations that were different to the other three parts. Its total coastline length decreased slightly from 239 km to 234.54 km during the forty-year time period. The island coastline decreased significantly, from 142.81 km in 1978 to 60.58 km in 2018. The mainland coastline increased sharply during the time period. In Part IV, land reclamation filled the gap between the mainland and island, whereby the island coastline became mainland coastline and led to coastline variations of this area.

3.3. Fractal Dimension

The

Table 5. Fractal dimension and R² of the PREA, including all coastline types, from 1978 to 2018.

Different Types of Coastline			1978	1988	1997	2008	2018
The PREA		FD	1.228	1.240	1.254	1.255	1.263
		R2	0.999	0.998	0.999	0.999	0.999
Mainland		FD	1.092	1.152	1.151	1.136	1.145
		R2	0.999	0.997	0.999	0.999	0.999
Islands		FD	1.138	1.161	1.181	1.187	1.200
		R2	1	0.999	0.999	0.999	0.999
Estuaries	Humen	FD	1.041	1.014	1.009	1.012	1.009
		R2	0.995	1	1	1	1
	Jiaomen	FD	1.023	1.013	1.020	1.018	1.027
		R2	0.999	0.999	0.999	0.999	0.999
	Hongqimen	FD	1.052	1.021	1.020	1.022	1.027
		R2	0.998	0.999	0.999	0.999	0.999
	Hengmen	FD	1.095	1.046	1.040	1.046	1.036
		R2	0.998	0.999	0.999	0.998	0.999
	Modaomen	FD	1.013	1.011	1.015	1.013	1.011
		R2	0.999	0.999	0.999	0.999	1
	Jitimen	FD	1.097	1.052	1.063	1.061	1.048
		R2	0.997	0.997	0.997	0.997	0.998
	Hutiaomen	FD	1.076	1.044	1.042	1.042	1.046
		R2	0.999	0.999	0.999	0.999	0.998
	Yamen	FD	1.011	1.002	1.006	1.001	1.001
		R2	0.999	1	0.999	1	0.999

and

Table 6. Fractal dimension and R² of the PREA, including all coastline types, from 1978 to 2018.

Different Part of the Main Body			1978	1988	1997	2008	2018
Part I	Total	FD	1.112	1.123	1.132	1.141	1.148
		R2	0.999	0.999	0.999	0.999	0.999
	Mainland	FD	1.073	1.090	1.098	1.108	1.118
		R2	0.999	0.999	0.999	0.999	0.999
	Island	FD	1.099	1.099	1.106	1.109	1.104
		R2	0.996	0.998	0.999	0.993	0.993
Part II	Total	FD	1.267	1.307	1.308	1.301	1.301
		R2	0.999	0.996	0.996	0.997	0.997
	Mainland	FD	1.053	1.111	1.125	1.124	1.129
		R2	0.999	0.996	0.996	0.997	0.996
	Island	FD	1.193	1.186	1.204	1.200	1.206
		R2	0.999	0.998	0.998	0.998	0.998
Part III	Total	FD	1.191	1.193	1.236	1.218	1.225
		R2	0.998	0.999	0.999	0.998	0.998
	Mainland	FD	1.040	1.094	1.090	1.082	1.087
		R2	0.999	0.998	0.999	1	0.999
	Island	FD	1.127	1.168	1.217	1.193	1.173
		R2	0.991	0.998	0.998	0.997	0.999
Part IV	Total	FD	1.128	1.118	1.134	1.1367	1.125
		R2	0.999	0.999	0.998	0.999	0.999
	Mainland	FD	1.055	1.097	1.114	1.114	1.099
		R2	0.999	0.999	0.998	0.999	0.999
	Island	FD	1.109	1.092	1.075	1.080	1.046
		R2	0.999	0.999	0.999	0.999	0.998

values show that all confidence levels (R²) were greater than 0.99, indicating that coastlines in the PREA can be described using fractal theory [41,43].

Table 5 describes the FD of the PREA, mainland, island, and estuaries. It is clear that the fractal dimension of coastlines, including the entire study area, mainland, island, and Jiaomen shows a growth, with some fluctuations during the time period. Table 6 includes the FD of four parts of the main body shown in Figure 1. Each part included the FD of the entire part, mainland coastline, and island coastline. As FD represented the complexity of the coastline, we can infer that the complexity of the PREA increased during the study period. Furthermore, we found that the island coastline showed the greatest complexity and the mainland showed the second most complexity when comparing different coastline types. All estuary coastlines demonstrated the least complexity.

It can be seen from Table 5 and Table 6 that the FD of the PREA has the largest value, from 1.228 in 1978 to 1.263 in 2018 compared with the other three different coastline types of the PREA. The island coastline demonstrated the largest FD compared with the other two types that increased from 1.138 in 1978 to 1.200 in 2018. Some fluctuations could be found on the mainland coastline, where the FD increased from 1.092 in 1978 to 1.152 in 1988, decreased to 1.136 in 2008, and then increased to 1.145 in 2018. It is clear that the FD of estuaries was the smallest among the three different coastline types, decreasing slightly during the period, with the exception of Jiaomen.

When combining Table 5 and Figure 5, the FD of the estuary coastline remained between 1.00 and 1.10. All estuaries exhibited a decline during the study period, with the exception of Jiaomen, which increased from 1.023 in 1978 to 1.027 in 2018. In 1978, this value differed significantly for Jitimen, with the maximum value of 1.097 and Yamen with the minimum value of 1.011. Nevertheless, the difference reduced in 2018. A sharp decline was found during the first decade, from 1978 to 1988. After 1988, the FD of the estuaries exhibited a gradual decrease in the following decades. Based on the complexity reflected by the FD, the complexity of the coastline of the estuaries in 2018 could be found as: Jitimen > Hutiaomen > Hengmen > Hongqimen > Jiaomen > Modaomen > Humen > Yamen.

Figure 6 and Figure 7 describe the mainland and island FD of Parts I–IV and the PRE, respectively. In Figure 6, Part I shows a different changing trend compared with other parts. Parts II–IV exhibit nearly the same trend of the PREA, with fluctuations. For Part I, the FD climbed dramatically during the period without fluctuations. In addition, the mainland of the PREA holds the largest FD value which refers to the mainland of the PREA showing a stronger complexity than the mainland coastline of Parts I–IV. Part II had the largest FD value in 1978, reaching 1.1286. Based on the complexity reflected by the FD, the complexity of the mainland coastline among Parts I–IV in 2018 could be found as: Part II > Part I > Part IV > Part III.

Figure 7 shows that different parts demonstrated different characteristics of FD. Part II obtained approximately the same trend as the PREA, but different from the mainland, the island of Part II had a larger FD value than the PREA, even though the value of the two was nearly the same in 2018. Part III had an increase in FD with significant fluctuations, reaching 1.217 in 1997, which was the largest value in this year. Part I increased slightly from 1.099 in 1978 to 1.104 in 2018. Part IV was the only part to show a FD decline among these four parts. The FD of Part IV dropped to 1.0457 in 2018, making it the fourth most complex. The complexity of the island coastline among Parts I–IV in 2018 could be described as: Part II > Part III > Part I > Part IV.

Figure 8a–d described the FD of Parts I–IV. The island coastline generally obtained a larger FD value than the mainland coastline among these four parts. The FD of the PREA also presented this phenomenon (Figure 5). Furthermore, the island FD in Part IV decreased during the forty-year time period. Combined with Table 4, we found that the island coastline length of Part IV decreased throughout the time period, but Parts I–III increased. From this, we suggest that there are some relationships between coastline length and FD.

3.4. Relationship Between Coastline Length and FD

Figure 9 demonstrates the changing trend of coastline length and FD for all types of coastline. When examining the relationship between coastline length and FD, it is found that the variation trend between coastline length and FD of the PREA, mainland, island, and Jiaomen is similar. For other estuaries, these two parameters are inconsistent with Figure 8. The coastline complexity of Humen, Hongqimen, Hengmen, Modaomen, Jitimen, Hutiaomen, and Yamen, therefore, did not correspond with the coastline length change.

Figure 10 describes the changing trend of coastline length and FD of the different parts of the main body, from Part I–IV. Nearly all the figures (Figure 10a–l) show that the FD of these parts was almost consistent with coastline length. Therefore, for the main body, the increased coastline length represents a more complex coastal boundary and the decreased coastline length represents a less complex coastal boundary.

4. Discussion

4.1. Driving Factors of Coastline Variations

Coastline changes are mainly influenced by natural and anthropogenic factors. Coastal erosion and accretion are natural factors leading to coastlines variations. Other natural factors such as sediment transport, tidal condition, wind, temperature, flow direction, and wave energy also lead to coastline variations [44,45,46,47]. In addition to these natural factors, anthropogenic factors also influence the length of coastlines.

In this study, we found that the coastline of the PREA increased significantly by 197 km, from 1133.43 km to 1349.73 km during the 40-year time period studied. The mainland coastline increased by 139 km, the island coastline increased by 65 km, and the coastline of the estuaries increased by 1–10 km.

In the PREA, the mainland and island coastlines were mainly influenced by anthropogenic factors, particularly land reclamation. Since 1978, land reclamation increased in the PREA [48], producing more land resources and longer artificial coastlines. To some extent, increased artificial coastlines will facilitate an increase in total coastline length. In the entire PREA, land filling was quite common over the forty years, and led to increased land area between the mainland and the island.

Parts I–IV showed different coastline change characteristics. The coastlines of Part I mainland, Part II island, Part III island, and Part IV mainland were mainly impacted by land reclamation and increased coastline length to create more land resources. The significantly increased Part IV mainland coastline length is seen in Table 4, with a sharp decrease of Part IV island coastline length. In this part, more land was generated seawards and the gap between the mainland coastline and the island was filled to satisfy the demand for land. Although different parts showed different coastline change trends, land reclamation was the most significant reason leading to this phenomenon.

Unlike the mainland and the island, the coastline of the estuaries was impacted primarily by natural factors with some anthropogenic factors, which have increased gradually during the past four decades. From the coastline extraction, we found that less land reclamation was found around estuaries; therefore, coastline erosion and sediment transport would be the most important factors. Sediment transport via the eight estuaries could reach 3.04 × 10⁷ ton per year [35]. A large amount of sediment transport may cause erosion of the PREA. Heise et al. (2010) assumed that a larger amount of sediment was deposited in the PREA than was eroded [49]. Furthermore, dams also impact upon sediment flux [50]. Dai et al. (2008) found that the sediment flux of the Pearl River had decreased since the 1980s [50] and suggested that more sediment was deposited in the reservoirs. As more dams were established in the PREA, less sediment flux would be transported into the sea. Wu et al. also indicated that human activities influence the sediment load carried into the sea [33]. For the coastline of estuaries, anthropogenic factors would therefore influence coastline length indirectly by influencing sediment transport.

The driving factors of coastline length of the PREA depend on different coastline types. Mainland and island coastlines are mainly influenced by land reclamation, but for estuary coastlines, the reason for their variations in length is mainly influenced by natural factors including erosion and sediment transport, and indirectly by human activities.

4.2. Driving Factors of FD Variations

The fractal dimension can reflect the complexity of a coastline; therefore, a changed coastline length would lead to a variation in coastline complexity. Figure 8 and Figure 9 demonstrate that coastline length and FD generally had the same trend during the study period. When the coastline length increased, the FD also increased. For estuaries, the trend between the coastline length and the FD was different, with the exception of Jiaomen.

As we analyzed the most significant influences of coastline length, it became apparent that the mainland and the island experienced land reclamation. As more artificial coastline was created around these two types of coastline, the shape of the coastal boundary changed simultaneously. This also led to the variation in coastline complexity, which was reflected by the FD. Increased artificial coastlines facilitate increased total coastline length and also lead to increased FD. A study by Zhang et al. (2015) reached a similar conclusion, whereby the coastline length became longer and the coastline FD of all China increased, with fluctuations as the proportion of artificial coastlines increased over the past forty years [39]. At this time, the original coastline became more complex, although it became smoother after building a wharf, an airport, and other facilities. In addition to the PREA, studies of the Yellow River Delta and all of China also found that as the complexity of coastlines increased, the proportion of smoother artificial coastline simultaneously increased. It could be considered that the total length of coastline grew as the length of artificial coastlines increased, and led to increased coastline complexity. Figure 9 shows detailed information of the mainland and island FD variations and also indicates that the complexity of coastline and coastline length show almost the same changing trend. Therefore, as the length of mainland and island coastline increased, the increased complexity reflects the increasing trend of the FD.

For the four parts of the main body, the eastern coast had a less complex coastline than the western coast. Parts II and III had a larger FD than the other two areas (Table 3). The western part (Part II and IV) included eight estuaries and described a larger FD than the eastern part. The location of eight estuaries might be one of the natural influences leading to the differing FD among these four parts because sediment deposition would affect the FD. It was observed that Parts II and III had a larger FD than the other two parts, indicating that these two areas displayed a more complex coastline. The coastline length of Parts II and III changed more significantly than Parts I and II (Table 3). Land reclamation and the artificial coastline have increased at the Pearl River Estuary since 1978, and Parts II and III were influenced more by human factors. Anthropogenic activities could, therefore, be a significant reason for the different FD of the different locations.

In contrast to the mainland and island coastlines, the FD of estuaries found a different trend compared with coastline length (Figure 8). The analysis showed that the coastline length of the estuaries remained almost stable, with a slight increase of 1–10 km. Compared with the mainland and island coastlines, little land reclamation would be found among the eight estuaries, and thus the variation of the FD of the estuaries was impacted more by natural factors.

Sediment deposition may decrease the complexity of estuary coastlines because less sediment flux flows past estuaries and the coastline becomes rougher with a more complex condition [46]. In 2008, Su et al. commented that the geographic locations of objects and coastline variations would influence the FD [40]. In light of this, different locations of estuaries may lead to different coastline complexities. Furthermore, the shape of the coastline might be changed by natural factors, and the coastline complexity among the eight estuaries may be reduced. Coastal erosion and sediment transport are the most two significant factors that impact upon the complexity of the coastline.

In general, the FD variations in the PREA were caused by comprehensive natural driving factors, overlaid with anthropogenic factors. Different types of coastlines are influenced by different factors. Here, land reclamation, accompanied by an intense demand for land for economic development, infrastructure construction, and rapid urbanization in this area were the main factors driving the change of coastline complexity of the mainland and the island. Geographic location, coastal erosion, and sediment transport were the main factors in the estuaries. For Parts I–IV, the FD was mainly caused by land reclamation and different areas showed different coastline complexity. The complexity of the eastern coast (Part I) showed less complexity than the western parts (Parts II–IV).

4.3. Relationship Between Coastline Length and FD

Figure 9 and Figure 10 demonstrate coastline length and FD variations of the PREA, mainland, island, estuaries, and Parts I–IV. In this section, further analysis of the relationship between coastline length and FD was conducted.

As shown, variations of coastline length and FD have nearly the same trend that increased during the time period. Figure 11 described a linear relationship between these two indicators of the coastlines in the entire PREA, mainland, island, and all estuaries. The closer the R² (coefficient of correlation) is to 1, the higher the correlation between these two indicators. This study found a positive correlation between the PREA, mainland, island, and two of the estuaries, including Jiaomen and Hutiaomen (>0.5). The remaining locations obtained a R² of <0.5 which is too weak to show a correlation between the coastline length and the FD. Among the areas with a positive relationship between coastline length and FD, the mainland coastline, island coastline, and Jiaomen also showed a consistent trend between these two parameters.

When combined with Figure 12, it is clear that the mainland and the island indicated a better relationship between coastline length and FD because the coastline length and the FD of the mainland and the island show almost the same trend as in Figure 10. The coastline length and complexity were impacted by land reclamation. A more regular artificial coastline was created during the study period, and the mainland and island coastlines were more significantly affected by anthropogenic factors. For these reasons, a positive relationship occurred between the length and FD of the mainland coastline, island coastline, and the majority of the Parts I–IV coastline.

The estuary coastline experiences less influence from artificial factors but more from natural factors. Although a rougher coastline was found around these areas, the coastline length of the estuaries remained mostly stable. Therefore, a negative relationship was found between the coastline length and the coastline complexity of the estuaries.

As the development of the PREA is still in progress, more land reclamation may occur around the mainland and island coastlines in the future; therefore, the complexity of these two types of coastline is likely to increase as the coastline increases. For the estuaries, due to the impacts of erosion, sediment transport, and dams, the complexity of this coastline is likely to decrease and the relationship between coastline length and FD may become weaker.

5. Conclusions

This study extracted coastlines of the mainland, island, and estuaries of the PREA using automatic and visual interpretation methods from Landsat data for 1978, 1988, 1997, 2008, and 2018. We reclassified the PREA as mainland and island coastline, and reclassified the main body of the PREA as Part I, Part II, Part III, and Part IV. We calculated their lengths and the FD of different coastlines using the box-counting method. The precision test for the coastline extracted in this study met the standard of precision evaluation proposed by Hou et al. (2016).

During the study period, the coastline length and the FD of the entire PREA increased significantly, with nearly the same tendency. A positive relationship between the coastline length and the FD was observed in the entire PREA, mainland, island, and two estuaries, including Jiaomen and Hutiaomen. Both the coastline length and complexity of these particular coastlines have increased over the past four decades, implying that these longer coastlines have led to a larger FD value and greater complexity. The island coastline was the most complex according to the FD result. The estuary coastline was the least complex coastline of the PREA. For the four parts of the main body, the eastern coast had a less complex coastline than the western coast. Parts II and III had a larger FD than the other two areas.

Land reclamation had the greatest influence on FD variations for the mainland and island coastlines. We found that more land filling occurred in the mainland and island, which changed the coastlines of these two areas, but land reclamation was rarely found around the estuaries. Land reclamation may increase the complexity of the coastline from previous studies. The FD value of Parts II and III indicated that more land reclamation was generated in these two areas because they had larger FD values.

For the coastline of the estuaries, coastal erosion, sediment transport, dam establishment, and other geographic objects were the main reasons for the FD variations. The complexity of the estuaries decreased as the sediment flux declined. The FD was mainly influenced by natural factors.

A different relationship between the coastline length and the FD was found among the mainland, island, and estuary coastlines. A positive relationship between length and FD was found for the mainland and the island. Nearly all estuaries showed a negative relationship between length and FD. As more land reclamation occurs around the PREA, government and citizens need to understand the importance of protecting ecosystems and finding a balance between ecological protection and economic development.