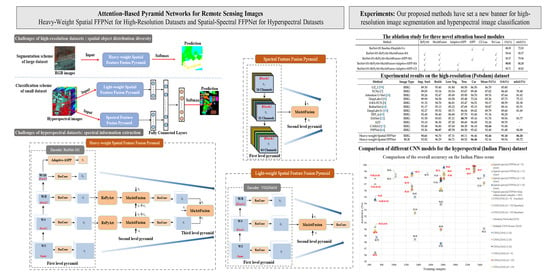
Attention-Based Pyramid Network for Segmentation and Classification of High-Resolution and Hyperspectral Remote Sensing Images
Abstract
:1. Introduction
- Missing pixels or occlusion of objects: different from traditional (RGB) imaging methods, remote sensing examines an area from a significantly long distance and gathers information and images remotely. Due to the large areas contained in one sample and the effects of the atmosphere, clouds, and shadows, missing pixels or occlusion of objects are inevitable problems in remote sensing images.
- Geometric size diversity: the geometric sizes of different objects may vary greatly and some objects are small and crowded in remote sensing imagery because of the large area covered comprising different objects (e.g., cars, trees, buildings, roads in Figure 1).
- High intra-class variance and low inter-class variance: this is a unique problem in remote sensing images and it inspires us to study superior methods aiming to effectively fuse multiscale features. For example, in Figure 1, buildings commonly vary in shape, style, and scale; low vegetations and impervious surfaces are similar in appearance.
- Spectral information extraction: hyperspectral image datasets contain hundreds of spectral bands, and it is challenging to extract spectral information because of the similarity between the spectral bands of different classes and complexity of the spectral structure, leading to the Hughes phenomenon or curse of dimensionality [7]. More importantly, hyperspectral datasets usually contain a limited number of labeled samples, thus making it difficult to extract effective spectral information from hyperspectral images.
- A.
- Review of Semantic Segmentation of High-resolution Remote Sensing Images by Multiscale Feature Processing.
- (1)
- Most models only consider the fusion of two or three adjacent scales and do not further consider how to achieve the feature fusion of more or even all the different scale layers. Improved classification accuracy can be achieved by combining useful features at more scales.
- (2)
- Although a small part of the attention mechanism (such as GFF [31]) considers the fusion of more layers, it does not successfully solve the semantic gaps between high- and low-level features. The detailed analysis of different feature layers is discussed in Section 2.1.
- (3)
- The novel attention mechanisms based on self-attention mainly focus on spatial and channel relations for semantic segmentation (such as the non-local network [21]). Regional relations are not considered for the remote sensing images, and thus the relationship between object regions cannot be deepened.
- B.
- Review of Spatial-spectral Classification for Hyperspectral Images by Multiscale Feature Processing.
- (1)
- When dealing with hyperspectral spatial neighborhoods of the considered pixel, the semantic gap in multiscale convolutional layers is not considered, and simple fusion is not the most effective strategy.
- (2)
- The spectral redundancy problem is not considered sufficiently in the existing hyperspectral classification models. With regard to such a complex spectral distribution, there is exceedingly little work on extraction of spectral information from coarse to fine (multiscale) processing by different channel dimensions.
- C.
- Contributions.
- (1)
- We propose attention-based multiscale fusion to fuse useful features at different and the same scales to achieve the effective extraction and fusion of spatial multiscale information and extraction of spectral information from coarse to fine scales.
- (2)
- We propose cross-scale attention in our adaptive atrous spatial pyramid pooling (adaptive-ASPP) network to adapt to varied contents in a feature-embedded space, leading to effective extraction of the context features.
- (3)
- A region pyramid attention module based on region-based attention is proposed to address the target geometric size diversity in large-scale remote sensing images.
2. Proposed Spatial-Spectral FFPNet
2.1. Overview
2.2. Region Pyramid Attention Module
2.2.1. Region Pyramid
2.2.2. Self-Attention on The Regional Representation
2.3. Multi-Scale Attention Fusion
2.3.1. Higher- and Lower-scales
2.3.2. Attention Fuse Module
2.4. Adaptive-ASPP Module
Cross-Scale Attention Module
2.5. Heavy-Weight Spatial FFPNet Model
2.6. Spatial-Spectral FFPNet Model
2.6.1. Light-Weight Spatial Feature Fusion Pyramid Module
2.6.2. Spectral Feature Fusion Pyramid Module
2.6.3. Merge
3. Experiments
3.1. Dataset Description and Baselines
3.1.1. High-Resolution Datasets
3.1.2. Hyperspectral Datasets
3.1.3. Baselines
3.2. Evaluation Metrics
3.3. Heavy-Weight Spatial FFPNet Evaluation on High-Resolution Datasets
3.3.1. Implementation Details
3.3.2. Experiments on Vaihingen Dataset
3.3.3. Experiments on Potsdam Dataset
3.4. Spatial-Spectral FFPNet Evaluation on Hyperspectral Datasets
3.4.1. Implementation Details
3.4.2. Ablation Study
3.4.3. Comparison with Existing CNN Methods
- (1)
- CNNs by Chen et al. [41]: First, the model configuration includes 1-D, 2-D, and 3-D CNNs. The 1-D CNN consists of five convolutional layers with ReLU and five pooling layers for the IP dataset as well as three convolutional layers with ReLU and three pooling layers for the UP dataset; the 1-D CNN extracts only spectral information. The 2-D CNN contains three 2D convolutional layers and two pooling layers. The latter two 2-D convolutional layers use the dropout strategy to prevent overfitting. The 3-D CNN is designed to effectively extract spatial and spectral information. It includes three 3D convolution and ReLU nonlinear activation layers, and the dropout strategy is also used to prevent overfitting. Overall, the design of the proposed model represents the early application of DCNN methods in hyperspectral image classification. However, although the models are simple and effective, the spatial and spectral distribution diversities of hyperspectral datasets are not considered. Second, in training settings, 1765 labeled samples were used as the training set for the IP dataset and 3930 samples as the training set for the UP dataset. Furthermore, experiments were conducted with different patch sizes (d = 9, 19, 29 for the IP dataset; d = 15, 21, 27 for the UP dataset) in the baseline [40].
- (2)
- CNN by Paoletti et al. [40]: The CNN model serves as the baseline model for our hyperspectral experiments. First, in the model configuration, to extract hyperspectral classification features, three 3D convolutional layers (i.e., , , for the IP dataset, and , , for the UP dataset) are designed, and each convolution layer is followed by a ReLU function. To reduce the spatial resolution, the first two convolution layers are followed by two max pooling. In addition, to prevent overfitting, the dropout method is executed in the first two convolution layers of the model, with probability = 0.1 for the IP dataset and 0.2 for the UP dataset. Next, a four-layer full connection classifies the extracted features. Although the 3D model requires less parameters and layers, it cannot address the diversity problem of spatial object distribution in hyperspectral data and cannot make the full use of spectral information. In addition, 3D convolution processes hyperspectral data are uniform volumetric data, while the hyperspectral actual object distribution is asymmetrical. Second, in the training setting, detailed experiments were conducted on different training samples and different patch sizes for the IP and UP datasets. The best experimental results of the baseline model (patch sizes d = 9, 19, and 29 with training samples = 2466 for the IP dataset; patch size d = 15, 21, and 27 with training samples = 1800 for the UP dataset) were considered for the comparison of the models.
- (3)
- Attention networks [45]: A visual attention-driven mechanism applied to residual neural networks (ResNet) facilitates spatial-spectral hyperspectral image classification. Specifically, the attention mechanism is integrated into the residual part of ResNet, which mainly includes two parts, namely the trunk and mask. The trunk consists of some residual blocks that perform feature extraction from the data, while the mask consists of a symmetrical downsampler–upsampler structure to extract useful features from the current layer. Although the attention mechanism has been successfully applied to ResNet, this attention method does not solve the problems of spatial distribution (the different geometric shapes of the objects) and spectral redundancy of hyperspectral data. Second, the network was optimized using 1537 training samples with 300 epochs for the IP dataset and 4278 training samples with 300 epochs for the UP dataset.
- (4)
- Multiple CNN fusion [42]: Compared with other models, although the multiscale spectral and spatial feature fusion model is time-consuming, it can achieve superior classification accuracy and hence has been gaining prominence in hyperspectral image classification. For example, Zhao et al. [42] presented a multiple convolutional layers fusion framework, which fuses features extracted from different convolutional layers for hyperspectral image classification. This multiple CNN model only considers the fusion of spatial features at different scales, but not the effective extraction of spatial and spectral features at multiple scales. Specifically, the multiscale spectral and spatial feature fusion model is divided into two types according to the fusion mechanism. The first one is the side output decision fusion network (SODFN), which applies majority voting to many side classification maps generated by each convolutional layer. The other one is the fully convolutional layer fusion network (FCLFN), which combines all features generated by each convolutional layer. Second, the SODFN and FCLFN parameters were tuned using 1029 training samples for the IP dataset and 436 training samples for the UP dataset.
4. Conclusions
5. Code and Model Availability
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ghamisi, P.; Mura, M.D.; Benediktsson, J.A. A Survey on Spectral–Spatial Classification Techniques Based on Attribute Profiles. IEEE Trans. Geosci. Remote Sens. 2015, 53, 2335–2353. [Google Scholar] [CrossRef]
- Wei, K.; Ouyang, C.; Duan, H.; Li, Y.; Chen, M.; Ma, J.; An, H.; Zhou, S. Reflections on the catastrophic 2020 Yangtze River Basin flooding in southern China. Innovation 2020, 1, 100038. [Google Scholar] [CrossRef]
- Wang, N.; Chen, F.; Yu, B.; Qin, Y. Segmentation of large-scale remotely sensed images on a Spark platform: A strategy for handling massive image tiles with the MapReduce model. ISPRS J. Photogramm. Remote Sens. 2020, 162, 137–147. [Google Scholar] [CrossRef]
- Sun, W.; Wang, R. Fully convolutional networks for semantic segmentation of very high resolution remotely sensed images combined with DSM. IEEE Geosci. Remote Sens. Lett. 2018, 15, 474–478. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, B.; Wang, L.; Bai, J.; Xiang, S.; Pan, C. Semantic labeling in very high resolution images via a self-cascaded convolutional neural network. ISPRS J. Photogramm. Remote Sens. 2018, 145, 78–95. [Google Scholar] [CrossRef] [Green Version]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Deep learning for classification of hyperspectral data: A comparative review. IEEE Geosci. Remote Sens. Mag. 2019, 7, 159–173. [Google Scholar] [CrossRef] [Green Version]
- Melgani, F.; Bruzzone, L. Classification of hyperspectral remote sensing images with support vector machines. IEEE Trans. Geosci. Remote Sens. 2014, 42, 1778–1790. [Google Scholar] [CrossRef] [Green Version]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Mou, L.; Hua, Y.; Zhu, X.X. A relation-augmented fully convolutional network for semantic segmentation in aerial scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 12416–12425. [Google Scholar]
- Chen, L.C.; Papandreou, G.; Kokkinos, I.; Murphy, K.; Yuille, A.L. Deeplab: Semantic image segmentation with deep convolutional nets, atrous convolution, and fully connected crfs. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 40, 834–848. [Google Scholar] [CrossRef]
- Chen, L.C.; Zhu, Y.; Papandreou, G.; Schroff, F.; Adam, H. Encoder-decoder with atrous separable convolution for semantic image segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 801–818. [Google Scholar]
- Wang, H.; Wang, Y.; Zhang, Q.; Xiang, S.; Pan, C. Gated convolutional neural network for semantic segmentation in high-resolution images. Remote Sens. 2017, 9, 446. [Google Scholar] [CrossRef] [Green Version]
- Cheng, G.; Wang, Y.; Xu, S.; Wang, H.; Xiang, S.; Pan, C. Automatic road detection and centerline extraction via cascaded end-to-end convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3322–3337. [Google Scholar] [CrossRef]
- Cheng, W.; Yang, W.; Wang, M.; Wang, G.; Chen, J. Context aggregation network for semantic labeling in aerial images. Remote Sens. 2019, 11, 1158. [Google Scholar] [CrossRef] [Green Version]
- Li, P.; Lin, Y.; Schultz-Fellenz, E. Contextual Hourglass Network for Semantic Segmentation of High Resolution Aerial Imagery. arXiv 2018, arXiv:1810.12813. [Google Scholar]
- Yang, X.; Yang, J.; Yan, J.; Zhang, Y.; Zhang, T.; Guo, Z.; Sun, X.; Fu, K. Scrdet: Towards more robust detection for small, cluttered and rotated objects. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 8232–8241. [Google Scholar]
- Sebastian, C.; Imbriaco, R.; Bondarev, E.; de With, P.H. Adversarial Loss for Semantic Segmentation of Aerial Imagery. arXiv 2020, arXiv:2001.04269. [Google Scholar]
- Dong, R.; Pan, X.; Li, F. DenseU-net-based semantic segmentation of small objects in urban remote sensing images. IEEE Access 2019, 7, 65347–65356. [Google Scholar] [CrossRef]
- Du, Y.; Song, W.; He, Q.; Huang, D.; Liotta, A.; Su, C. Deep learning with multi-scale feature fusion in remote sensing for automatic oceanic eddy detection. Inf. Fusion 2019, 49, 89–99. [Google Scholar] [CrossRef] [Green Version]
- Jain, S.; Wallace, B.C. Attention is not explanation. arXiv 2019, arXiv:1902.10186. [Google Scholar]
- Wang, X.; Girshick, R.; Gupta, A.; He, K. Non-local neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 7794–7803. [Google Scholar]
- Fu, J.; Liu, J.; Tian, H.; Li, Y.; Bao, Y.; Fang, Z.; Lu, H. Dual attention network for scene segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 3146–3154. [Google Scholar]
- Zhu, Z.; Xu, M.; Bai, S.; Huang, T.; Bai, X. Asymmetric non-local neural networks for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 593–602. [Google Scholar]
- Oktay, O.; Schlemper, J.; Folgoc, L.L.; Lee, M.; Heinrich, M.; Misawa, K.; Mori, K.; McDonagh, S.; Hammerla, N.Y.; Kainz, B.; et al. Attention u-net: Learning where to look for the pancreas. arXiv 2018, arXiv:1804.03999. [Google Scholar]
- Huang, Z.; Wang, X.; Huang, L.; Huang, C.; Wei, Y.; Liu, W. Ccnet: Criss-cross attention for semantic segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 603–612. [Google Scholar]
- Zhang, F.; Chen, Y.; Li, Z.; Hong, Z.; Liu, J.; Ma, F.; Han, J.; Ding, E. ACFNet: Attentional Class Feature Network for Semantic Segmentation. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 6798–6807. [Google Scholar]
- Sindagi, V.A.; Patel, V.M. Multi-level bottom-top and top-bottom feature fusion for crowd counting. In Proceedings of the IEEE International Conference on Computer Vision, Seoul, Korea, 27 October–2 November 2019; pp. 1002–1012. [Google Scholar]
- Niu, R. HMANet: Hybrid Multiple Attention Network for Semantic Segmentation in Aerial Images. arXiv 2020, arXiv:2001.02870. [Google Scholar]
- Guo, C.; Fan, B.; Zhang, Q.; Xiang, S.; Pan, C. AugFPN: Improving Multi-scale Feature Learning for Object Detection. arXiv 2019, arXiv:1912.05384. [Google Scholar]
- Jin, X.; Lan, C.; Zeng, W.; Zhang, Z.; Chen, Z. CaseNet: Content-adaptive scale interaction networks for scene parsing. arXiv 2019, arXiv:1904.08170. [Google Scholar]
- Li, X.; Zhao, H.; Han, L.; Tong, Y.; Yang, K. GFF: Gated Fully Fusion for Semantic Segmentation. arXiv 2019, arXiv:1904.01803. [Google Scholar]
- Tarabalka, Y.; Benediktsson, J.A.; Chanussot, J. Spectral–Spatial Classification of Hyperspectral Imagery Based on Partitional Clustering Techniques. IEEE Trans. Geosci. Remote Sens. 2009, 47, 2973–2987. [Google Scholar] [CrossRef]
- Archibald, R.; Fann, G. Feature Selection and Classification of Hyperspectral Images With Support Vector Machines. IEEE Geosci. Remote Sens. Lett. 2007, 4, 674–677. [Google Scholar] [CrossRef]
- Sun, S.; Zhong, P.; Xiao, H.; Wang, R. Active Learning With Gaussian Process Classifier for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1746–1760. [Google Scholar] [CrossRef]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Hyperspectral Image Classification Using Dictionary-Based Sparse Representation. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3973–3985. [Google Scholar] [CrossRef]
- Makantasis, K.; Karantzalos, K.; Doulamis, A.; Doulamis, N. Deep supervised learning for hyperspectral data classification through convolutional neural networks. In Proceedings of the Deep Supervised Learning for Hyperspectral Data Classification Through Convolutional Neural Networks, Milan, Italy, 26–31 July 2015; pp. 4959–4962. [Google Scholar]
- Zhao, W.; Du, S. Spectral–Spatial Feature Extraction for Hyperspectral Image Classification: A Dimension Reduction and Deep Learning Approach. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4544–4554. [Google Scholar] [CrossRef]
- Luo, Y.; Zou, J.; Yao, C.; Li, T.; Bai, G. HSI-CNN: A Novel Convolution Neural Network for Hyperspectral Image. In Proceedings of the 2018 International Conference on Audio, Language and Image Processing (ICALIP), Shanghai, China, 16–17 July 2018. [Google Scholar]
- Li, Y.; Zhang, H.; Shen, Q. Spectral–Spatial Classification of Hyperspectral Imagery with 3D Convolutional Neural Network. Remote Sens. 2017, 9, 67. [Google Scholar] [CrossRef] [Green Version]
- Paoletti, M.; Haut, J.; Plaza, J.; Plaza, A. A new deep convolutional neural network for fast hyperspectral image classification. ISPRS J. Photogramm. Remote Sens. 2018, 145, 120–147. [Google Scholar] [CrossRef]
- Chen, Y.; Jiang, H.; Li, C.; Jia, X.; Ghamisi, P. Deep Feature Extraction and Classification of Hyperspectral Images Based on Convolutional Neural Networks. IEEE Trans. Geosci. Remote Sens. 2016, 54, 6232–6251. [Google Scholar] [CrossRef] [Green Version]
- Zhao, G.; Liu, G.; Fang, L.; Tu, B.; Ghamisi, P. Multiple convolutional layers fusion framework for hyperspectral image classification. Neurocomputing 2019, 339, 149–160. [Google Scholar] [CrossRef]
- Gong, Z.; Zhong, P.; Yu, Y.; Hu, W.; Li, S. A CNN With Multiscale Convolution and Diversified Metric for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 3599–3618. [Google Scholar] [CrossRef]
- Imani, M.; Ghassemian, H. An overview on spectral and spatial information fusion for hyperspectral image classification: Current trends and challenges. Inf. Fusion 2020, 59, 59–83. [Google Scholar] [CrossRef]
- Haut, J.M.; Paoletti, M.E.; Plaza, J.; Plaza, A.; Li, J. Visual Attention-Driven Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 8065–8080. [Google Scholar] [CrossRef]
- Mei, X.; Pan, E.; Ma, Y.; Dai, X.; Huang, J.; Fan, F.; Du, Q.; Zheng, H.; Ma, J. Spectral-Spatial Attention Networks for Hyperspectral Image Classification. Remote Sens. 2019, 11, 963. [Google Scholar] [CrossRef] [Green Version]
- Xu, Q.; Ouyang, C.; Jiang, T.; Fan, X.; Cheng, D. DFPENet-geology: A Deep Learning Framework for High Precision Recognition and Segmentation of Co-seismic Landslides. arXiv 2019, arXiv:1908.10907. [Google Scholar]
- Ronneberger, O.; Fischer, P.; Brox, T. U-net: Convolutional networks for biomedical image segmentation. In Proceedings of the International Conference on Medical Image Computing And Computer-Assisted Intervention, Munich, Germany, 5–9 October 2015; pp. 234–241. [Google Scholar]
- Lin, D.; Shen, D.; Shen, S.; Ji, Y.; Lischinski, D.; Cohen-Or, D.; Huang, H. ZigZagNet: Fusing Top-Down and Bottom-Up Context for Object Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Long Beach, CA, USA, 16–20 June 2019; pp. 7490–7499. [Google Scholar]
- Zhen, M.; Wang, J.; Zhou, L.; Fang, T.; Quan, L. Learning Fully Dense Neural Networks for Image Semantic Segmentation. In Proceedings of the AAAI Conference on Artificial Intelligence, Hilton Hawaiian Village, Honolulu, Hawaii, USA, 27 January–1 February 2019; Volume 33, pp. 9283–9290. [Google Scholar]
- Zhang, Z.; Zhang, X.; Peng, C.; Xue, X.; Sun, J. Exfuse: Enhancing feature fusion for semantic segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 269–284. [Google Scholar]
- Zhou, Z.; Siddiquee, M.M.R.; Tajbakhsh, N.; Liang, J. UNet++: Redesigning Skip Connections to Exploit Multiscale Features in Image Segmentation. IEEE Trans. Med. Imaging 2019, 39, 1856–1867. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Zhao, H.; Zhang, Y.; Liu, S.; Shi, J.; Change Loy, C.; Lin, D.; Jia, J. Psanet: Point-wise spatial attention network for scene parsing. In Proceedings of the European Conference on Computer Vision (ECCV), Munich, Germany, 8–14 September 2018; pp. 267–283. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Deng, J.; Dong, W.; Socher, R.; Li, L.J.; Li, K.; Fei-Fei, L. Imagenet: A large-scale hierarchical image database. In Proceedings of the 2009 IEEE Conference on Computer Vision and Pattern Recognition, Miami, FL, USA, 20–25 June 2009; pp. 248–255. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very deep convolutional networks for large-scale image recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Yang, M.; Yu, K.; Zhang, C.; Li, Z.; Yang, K. Denseaspp for semantic segmentation in street scenes. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 3684–3692. [Google Scholar]
- Srivastava, N.; Hinton, G.E.; Krizhevsky, A.; Sutskever, I.; Salakhutdinov, R. Dropout: A simple way to prevent neural networks from overfitting. J. Mach. Learn. Res. 2014, 15, 1929–1958. [Google Scholar]
- Volpi, M.; Tuia, D. Dense semantic labeling of subdecimeter resolution images with convolutional neural networks. IEEE Trans. Geosci. Remote Sens. 2016, 55, 881–893. [Google Scholar] [CrossRef] [Green Version]
- Lin, G.; Milan, A.; Shen, C.; Reid, I. RefineNet: Multi-Path Refinement Networks for High-Resolution Semantic Segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition CVPR, Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Audebert, N.; Le Saux, B.; Lefèvre, S. Beyond RGB: Very high resolution urban remote sensing with multimodal deep networks. ISPRS J. Photogramm. Remote Sens. 2018, 140, 20–32. [Google Scholar] [CrossRef] [Green Version]
- Badrinarayanan, V.; Kendall, A.; Cipolla, R. Segnet: A deep convolutional encoder-decoder architecture for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 2481–2495. [Google Scholar] [CrossRef] [PubMed]
- Marmanis, D.; Schindler, K.; Wegner, J.D.; Galliani, S.; Datcu, M.; Stilla, U. Classification with an edge: Improving semantic image segmentation with boundary detection. ISPRS J. Photogramm. Remote Sens. 2018, 135, 158–172. [Google Scholar] [CrossRef] [Green Version]
- Zhao, H.; Shi, J.; Qi, X.; Wang, X.; Jia, J. Pyramid scene parsing network. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 2881–2890. [Google Scholar]
- Sherrah, J. Fully convolutional networks for dense semantic labelling of high-resolution aerial imagery. arXiv 2016, arXiv:1606.02585. [Google Scholar]
- Pan, B.; Shi, Z.; Xu, X.; Shi, T.; Zhang, N.; Zhu, X. CoinNet: Copy initialization network for multispectral imagery semantic segmentation. IEEE Geosci. Remote Sens. Lett. 2018, 16, 816–820. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
















| Level | Detailed Configurations |
|---|---|
| First-level pyramid | : Conv2d(7 × 7)-1-64 + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 |
| : Maxpool + Block1(1 × 1 + 3 × 3 + 1 × 1)-3-256 + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 | |
| : Block2(1 × 1 + 3 × 3 + 1 × 1)-4-512 + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 | |
| : Block3(1 × 1 + 3 × 3 + 1 × 1)-23-1024 + Block4(1 × 1 + 3 × 3 + 1 × 1)-3-2048 + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 | |
| : Adaptive-ASPP | |
| Second-level pyramid | : RePyAtt + MuAttFusion(, , , ) + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 |
| : RePyAtt + MuAttFusion(, , , ) + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 | |
| Third-level pyramid | MuAttFusion(, , ) |
| Parameter: | 78.8 million |
| Level | Detailed Configurations |
|---|---|
| First-level pyramid | : Conv2d(3 × 3)-2-64 + Conv2d(3 × 3)-2-128 + Maxpool + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 |
| : Conv2d(3 × 3)-3-256 + Conv2d(3 × 3)-3-512 + Maxpool + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 | |
| : Conv2d(3 × 3)-3-512 + Maxpool + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 | |
| Second-level pyramid | MuAttFusion(, , ) + ResConv(1 × 1 + 3 × 3 + 3 × 3)-1-256 |
| Parameter | 24.8 million |
| Level | Detailed Configurations |
|---|---|
| First-level pyramid | : Conv2d(3 × 3 + 1 × 1)-1-64 |
| : Conv2d(3 × 3 + 1 × 1)-1-32 | |
| : Conv2d(3 × 3 + 1 × 1)-1-16 | |
| Second-level pyramid | MuAttFusion(, , ) |
| Parameter | 0.20 million |
| Method | RePyAtt | MuAttFusion | Adaptive-ASPP | ASPP | CE Loss | BA Loss | OA(%) | mIoU(%) |
|---|---|---|---|---|---|---|---|---|
| ResNet-101 Baseline (Deeplabv3+) | ✓ | ✓ | 88.09 | 72.83 | ||||
| ResNet-101 + RePyAtt + MuAttFusion + BA | ✓ | ✓ | ✓ | 90.64 | 80.37 | |||
| ResNet-101 + RePyAtt + MuAttFusion + ASPP + BA | ✓ | ✓ | ✓ | ✓ | 90.37 | 79.96 | ||
| ResNet-101 + RePyAtt + MuAttFusion + Adaptive-ASPP + BA | ✓ | ✓ | ✓ | ✓ | 90.91 | 81.33 | ||
| ResNet-101 + RePyAtt + MuAttFusion + Adaptive-ASPP + CE | ✓ | ✓ | ✓ | ✓ | 90.71 | 80.82 |
| Pyramid Combinations | OA(%) | mIoU(%) |
|---|---|---|
| {single pixel, 8, 4, 2, 1} | 90.28 | 79.63 |
| {single pixel, 4, 2, 1} | 90.91 | 81.33 |
| {single pixel, 2, 1} | 90.49 | 80.08 |
| {single pixel, 1} | 90.66 | 80.39 |
| Method | Imp. Surf. | Build. | Low Veg. | Tree | Car | Mean F1(%) | OA(%) | mIoU(%) |
|---|---|---|---|---|---|---|---|---|
| FCNs [8] | 88.11 | 91.36 | 77.10 | 85.70 | 75.03 | 83.46 | 85.73 | 72.12 |
| DeepLabv3 [10] | 87.75 | 92.04 | 77.47 | 85.85 | 65.21 | 81.66 | 86.48 | 70.05 |
| UZ_1 [59] | 89.20 | 92.50 | 81.60 | 86.90 | 57.30 | 81.50 | 87.30 | - |
| Attention U-Net [24] | 90.44 | 92.91 | 80.30 | 87.90 | 79.10 | 86.13 | 87.95 | 76.05 |
| DeepLabv3+ [11] | 90.03 | 93.13 | 79.08 | 87.09 | 68.94 | 83.65 | 88.09 | 72.83 |
| RefineNet [60] | 90.82 | 94.11 | 81.07 | 88.92 | 82.17 | 87.42 | 88.98 | 78.01 |
| S-RA-FCN [9] | 91.47 | 94.97 | 80.63 | 88.57 | 87.05 | 88.54 | 89.23 | - |
| ONE_7 [61] | 91.00 | 94.50 | 84.40 | 89.90 | 77.80 | 87.52 | 89.80 | - |
| DANet [22] | 91.63 | 95.02 | 83.25 | 88.87 | 87.16 | 89.19 | 89.85 | 80.53 |
| GSN5 [12] | 91.80 | 95.00 | 83.70 | 89.70 | 81.90 | 88.42 | 90.10 | - |
| DLR_10 [63] | 92.30 | 95.20 | 84.10 | 90.00 | 79.30 | 88.18 | 90.30 | - |
| PSPNet [64] | 92.79 | 95.46 | 84.51 | 89.94 | 88.61 | 90.26 | 90.85 | 82.58 |
| Heavy-weight Spatial FFPNet | 92.80 | 95.24 | 83.75 | 89.38 | 86.56 | 89.55 | 90.91 | 81.33 |
| Method | Image Type | Imp. Surf. | Build. | Low Veg. | Tree | Car | Mean F1(%) | OA(%) | mIoU(%) |
|---|---|---|---|---|---|---|---|---|---|
| UZ_1 [59] | IRRG | 89.30 | 95.40 | 81.80 | 80.50 | 86.50 | 86.70 | 85.80 | - |
| FCNs [8] | IRRG | 89.05 | 93.34 | 83.54 | 83.67 | 89.48 | 87.82 | 86.40 | 78.48 |
| Attention U-Net [24] | IRRG | 90.26 | 92.47 | 85.49 | 85.90 | 94.70 | 89.76 | 87.64 | 81.62 |
| DeepLabv3 [10] | IRRG | 89.90 | 94.58 | 83.58 | 85.48 | 73.24 | 85.36 | 87.73 | 75.12 |
| S-RA-FCN [9] | IRRG | 91.33 | 94.70 | 86.81 | 83.47 | 94.52 | 90.17 | 88.59 | 82.38 |
| RefineNet [60] | IRRG | 91.17 | 95.13 | 85.22 | 87.69 | 95.15 | 90.87 | 89.16 | 83.51 |
| DeepLabv3+ [11] | IRRG | 92.27 | 95.52 | 85.71 | 86.04 | 89.42 | 89.79 | 89.60 | 81.69 |
| DST_6 [65] | IRRG | 92.40 | 96.40 | 86.80 | 87.70 | 93.40 | 91.34 | 90.20 | - |
| DANet [22] | IRRG | 91.50 | 95.83 | 87.21 | 88.79 | 95.16 | 91.70 | 90.56 | 83.77 |
| AZ3 | IRRG | 93.10 | 96.30 | 87.20 | 88.60 | 96.00 | 92.24 | 90.70 | - |
| CASIA3 [5] | IRRG | 93.40 | 96.80 | 87.60 | 88.30 | 96.10 | 92.44 | 91.00 | - |
| PSPNet [64] | IRRG | 93.36 | 96.97 | 87.75 | 88.50 | 95.42 | 92.40 | 91.08 | 84.88 |
| Heavy-weight Spatial FFPNet | IRRG | 93.61 | 96.70 | 87.31 | 88.11 | 96.46 | 92.44 | 91.10 | 86.20 |
| Heavy-weight Spatial FFPNet | RGB | 92.82 | 96.29 | 86.71 | 88.52 | 96.48 | 92.16 | 90.54 | 85.72 |
| IP | ||||||
|---|---|---|---|---|---|---|
| Class | Pixels | 200 Samples per Category | 150 Samples per Category | 100 Samples per Category | 50 Samples per Category | 200 Samples per Category in [40] |
| Alfalfa | 46 | 23 | 23 | 23 | 23 | 33 |
| Corn-notill | 1428 | 200 | 150 | 100 | 50 | 200 |
| Corn-mintill | 830 | 200 | 150 | 100 | 50 | 200 |
| Corn | 237 | 118 | 118 | 100 | 50 | 181 |
| Grass-pasture | 483 | 200 | 150 | 100 | 50 | 200 |
| Grass-trees | 730 | 200 | 150 | 100 | 50 | 200 |
| Grass-pasture-mowed | 28 | 14 | 14 | 14 | 14 | 20 |
| Hay-windrowed | 478 | 200 | 150 | 100 | 50 | 200 |
| Oats | 20 | 10 | 10 | 10 | 10 | 14 |
| Soybeans-notill | 972 | 200 | 150 | 100 | 50 | 200 |
| Soybeans-mintill | 2455 | 200 | 150 | 100 | 50 | 200 |
| Soybeans-clean | 593 | 200 | 150 | 100 | 50 | 200 |
| Wheat | 205 | 102 | 102 | 100 | 50 | 143 |
| Woods | 1265 | 200 | 150 | 100 | 50 | 200 |
| Bldg-grass-tree-drives | 386 | 193 | 150 | 100 | 50 | 200 |
| Stone-steel-towers | 93 | 46 | 46 | 46 | 46 | 75 |
| Total | 10,249 | 2306 | 1813 | 1293 | 693 | 2466 |
| UP | ||||||
|---|---|---|---|---|---|---|
| Class | Pixels | 200 Samples per Category | 150 Samples per Category | 100 Samples per Category | 50 Samples per Category | 200 Samples per Category in [40] |
| Asphalt | 6631 | 200 | 150 | 100 | 50 | 200 |
| Meadows | 18,649 | 200 | 150 | 100 | 50 | 200 |
| Gravel | 2099 | 200 | 150 | 100 | 50 | 200 |
| Trees | 3064 | 200 | 150 | 100 | 50 | 200 |
| Painted metal sheets | 1345 | 200 | 150 | 100 | 50 | 200 |
| Bare soil | 5029 | 200 | 150 | 100 | 50 | 200 |
| Bitumen | 1330 | 200 | 150 | 100 | 50 | 200 |
| Self-blocking bricks | 3682 | 200 | 150 | 100 | 50 | 200 |
| Shadows | 947 | 200 | 150 | 100 | 50 | 200 |
| Total | 42,776 | 1800 | 1350 | 900 | 450 | 1800 |
| Dataset | Patch Size | Total Time | Accuracy | ||
|---|---|---|---|---|---|
| OA | AA | Kappa | |||
| IP | d = 9 | 15.13 | 96.30 | 98.31 | 95.73 |
| d = 15 | 17.86 | 96.78 | 98.68 | 96.29 | |
| d = 19 | 14.66 | 98.50 | 99.16 | 98.27 | |
| d = 29 | 21.57 | 98.74 | 99.43 | 98.57 | |
| UP | d = 9 | 9.12 | 91.37 | 91.28 | 88.60 |
| d = 15 | 7.06 | 96.41 | 96.14 | 95.25 | |
| d = 21 | 8.16 | 98.82 | 98.37 | 98.44 | |
| d = 27 | 9.60 | 97.29 | 97.26 | 96.42 | |
| Sample Patch Size | d = 9 | d = 15 | d = 19 | d = 29 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Samples per Category | 50 | 100 | 150 | 200 | 50 | 100 | 150 | 200 | 50 | 100 | 150 | 200 | 50 | 100 | 150 | 200 |
| Alfalfa | 100.00 | 100.00 | 95.65 | 95.65 | 100.00 | 100.00 | 95.65 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Corn-notill | 73.66 | 95.63 | 98.83 | 98.78 | 74.38 | 94.65 | 98.51 | 99.35 | 83.16 | 99.32 | 99.53 | 99.59 | 87.11 | 99.72 | 100.00 | 100.00 |
| Corn-mintill | 72.69 | 98.63 | 98.97 | 99.84 | 86.03 | 97.40 | 99.71 | 98.25 | 97.44 | 96.30 | 99.56 | 99.05 | 95.65 | 100.00 | 100.00 | 100.00 |
| Corn | 93.58 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 98.93 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Grass-pasture | 90.76 | 98.96 | 98.80 | 100.00 | 97.46 | 99.48 | 100.00 | 100.00 | 93.07 | 97.65 | 98.80 | 98.94 | 95.83 | 98.33 | 100.00 | 100.00 |
| Grass-trees | 97.06 | 98.10 | 99.31 | 99.62 | 97.50 | 99.84 | 100.00 | 100.00 | 97.35 | 99.05 | 100.00 | 98.87 | 95.05 | 98.35 | 99.45 | 100.00 |
| Grass-pasture-mowed | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Hay-windrowed | 97.20 | 100.00 | 100.00 | 100.00 | 98.36 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Oats | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Soybeans-notill | 78.98 | 94.01 | 99.75 | 99.33 | 87.04 | 99.19 | 97.78 | 99.73 | 87.15 | 97.81 | 99.51 | 100.00 | 98.26 | 98.70 | 99.57 | 100.00 |
| Soybeans-mintill | 70.73 | 93.25 | 94.84 | 98.58 | 74.80 | 93.25 | 97.53 | 99.38 | 80.79 | 97.54 | 95.75 | 99.78 | 91.19 | 96.41 | 99.35 | 99.35 |
| Soybean-clean | 86.37 | 99.19 | 99.55 | 99.24 | 94.66 | 98.58 | 98.87 | 100.00 | 96.87 | 98.99 | 100.00 | 100.00 | 98.65 | 99.32 | 99.32 | 100.00 |
| Wheat | 98.71 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Woods | 94.07 | 97.94 | 98.57 | 98.78 | 96.79 | 98.63 | 99.64 | 99.34 | 93.83 | 99.91 | 100.00 | 100.00 | 98.73 | 100.00 | 99.68 | 100.00 |
| Bldg-grass-tree-drives | 99.11 | 97.20 | 100.00 | 100.00 | 98.51 | 97.90 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 96.88 | 100.00 | 100.00 | 100.00 |
| Stone-steel-towers | 100.00 | 100.00 | 100.00 | 95.74 | 100.00 | 100.00 | 100.00 | 100.00 | 97.87 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| OA | 82.12 | 96.30 | 97.98 | 99.07 | 86.44 | 96.78 | 98.74 | 99.47 | 89.79 | 98.50 | 98.63 | 99.68 | 94.65 | 98.74 | 99.69 | 99.84 |
| AA | 90.81 | 98.31 | 99.02 | 99.10 | 94.10 | 98.68 | 99.23 | 99.75 | 95.40 | 99.16 | 99.57 | 99.76 | 97.34 | 99.43 | 99.84 | 99.96 |
| Kappa | 79.65 | 95.73 | 97.65 | 98.90 | 84.56 | 96.29 | 98.53 | 99.38 | 88.35 | 98.27 | 98.41 | 99.63 | 93.93 | 98.57 | 99.64 | 99.82 |
| Run time | 9.24 | 15.13 | 20.39 | 22.55 | 8.21 | 17.86 | 28.47 | 31.44 | 10.37 | 14.66 | 23.12 | 34.05 | 15.43 | 21.57 | 27.41 | 37.38 |
| Sample Patch Size | d = 9 | d = 15 | d = 21 | d = 27 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Samples per Category | 50 | 100 | 150 | 200 | 50 | 100 | 150 | 200 | 50 | 100 | 150 | 200 | 50 | 100 | 150 | 200 |
| Asphalt | 66.14 | 88.65 | 95.72 | 96.32 | 78.03 | 94.57 | 98.19 | 98.19 | 93.54 | 97.34 | 98.97 | 97.59 | 92.28 | 91.61 | 99.70 | 99.82 |
| Meadows | 87.47 | 94.64 | 98.09 | 97.96 | 92.86 | 97.98 | 99.44 | 99.98 | 97.68 | 99.81 | 99.89 | 99.91 | 97.45 | 99.31 | 99.68 | 99.85 |
| Gravel | 49.62 | 90.27 | 97.14 | 95.99 | 91.03 | 96.37 | 99.43 | 98.66 | 89.12 | 98.09 | 99.81 | 99.81 | 93.32 | 98.66 | 99.05 | 99.05 |
| Trees | 57.44 | 86.03 | 87.86 | 90.60 | 59.79 | 92.95 | 96.08 | 96.61 | 72.19 | 94.39 | 94.39 | 96.34 | 83.16 | 93.34 | 94.26 | 96.61 |
| Painted metal sheets | 95.24 | 97.62 | 99.40 | 100.00 | 97.92 | 98.81 | 99.70 | 99.11 | 98.51 | 98.51 | 100.00 | 100.00 | 96.13 | 99.40 | 99.70 | 100.00 |
| Bare Soil | 18.46 | 87.59 | 96.26 | 93.95 | 60.14 | 98.41 | 99.68 | 100.00 | 94.99 | 99.68 | 100.00 | 100.00 | 95.78 | 100.00 | 100.00 | 100.00 |
| Bitumen | 94.88 | 98.49 | 99.40 | 97.59 | 98.49 | 98.80 | 99.40 | 100.00 | 97.59 | 100.00 | 100.00 | 100.00 | 97.59 | 100.00 | 100.00 | 100.00 |
| Self-Blocking Bricks | 36.96 | 84.46 | 95.98 | 96.30 | 36.74 | 90.00 | 98.70 | 99.02 | 77.39 | 99.24 | 97.28 | 98.04 | 71.09 | 93.91 | 97.72 | 99.13 |
| Shadows | 79.65 | 93.81 | 96.02 | 97.35 | 79.65 | 97.35 | 100.00 | 98.23 | 93.36 | 98.23 | 98.67 | 100.00 | 95.13 | 99.12 | 95.58 | 99.56 |
| OA | 67.99 | 91.37 | 96.58 | 96.51 | 79.47 | 96.41 | 98.99 | 99.25 | 92.66 | 98.82 | 99.12 | 99.15 | 92.87 | 97.29 | 99.05 | 99.53 |
| AA | 65.09 | 91.28 | 96.21 | 96.23 | 77.18 | 96.14 | 98.96 | 98.87 | 90.49 | 98.37 | 98.78 | 99.08 | 91.33 | 97.26 | 98.41 | 99.33 |
| Kappa | 56.52 | 88.60 | 95.47 | 95.37 | 72.73 | 95.25 | 98.66 | 99.01 | 90.24 | 98.44 | 98.83 | 98.87 | 90.55 | 96.42 | 98.75 | 99.38 |
| Run time | 4.91 | 9.12 | 13.23 | 15.48 | 4.79 | 7.06 | 12.40 | 14.05 | 4.90 | 8.16 | 11.50 | 14.55 | 5.04 | 9.60 | 13.66 | 18.45 |
| Methods | d = 9 | d = 15 | d = 19 | d = 29 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Class | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | |
| Alfalfa | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |
| Corn-notill | 73.66 | 82.22 | 74.38 | 89.84 | 83.16 | 96.81 | 87.11 | 98.60 | |
| Corn-min | 72.69 | 95.90 | 86.03 | 95.64 | 97.44 | 98.46 | 95.65 | 98.55 | |
| Corn | 93.58 | 98.40 | 100.00 | 100.00 | 98.93 | 100.00 | 100.00 | 98.31 | |
| Grass/Pasture | 90.76 | 91.69 | 97.46 | 97.00 | 93.07 | 94.46 | 95.83 | 95.83 | |
| Grass/Trees | 97.06 | 94.12 | 97.50 | 98.68 | 97.35 | 98.09 | 95.05 | 100.00 | |
| Grass/pasture-mowed | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |
| Hay-windrowed | 97.20 | 99.77 | 98.36 | 99.30 | 100.00 | 100.00 | 100.00 | 100.00 | |
| Oats | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |
| Soybeans-notill | 78.98 | 87.25 | 87.04 | 84.53 | 87.15 | 96.08 | 98.26 | 97.39 | |
| Soybeans-min | 70.73 | 84.24 | 74.80 | 93.43 | 80.79 | 94.97 | 91.19 | 94.62 | |
| Soybean-clean | 86.37 | 97.97 | 94.66 | 99.08 | 96.87 | 97.05 | 98.65 | 99.32 | |
| Wheat | 98.71 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | |
| Woods | 94.07 | 95.06 | 96.79 | 99.92 | 93.83 | 98.60 | 98.73 | 100.00 | |
| Bldg-Grass-Tree-Drives | 99.11 | 99.70 | 98.51 | 99.11 | 100.00 | 99.70 | 96.88 | 100.00 | |
| Stone-steel | 100.00 | 100.00 | 100.00 | 100.00 | 97.87 | 97.87 | 100.00 | 100.00 | |
| OA | 82.12 | 90.32 | 86.44 | 94.68 | 89.79 | 97.02 | 94.65 | 97.88 | |
| AA | 90.81 | 95.39 | 94.10 | 97.28 | 95.40 | 98.26 | 97.34 | 98.91 | |
| Kappa | 79.65 | 88.95 | 84.56 | 93.89 | 88.35 | 96.58 | 93.93 | 97.58 | |
| Methods | d = 9 | d = 15 | d = 21 | d = 27 | |||||
|---|---|---|---|---|---|---|---|---|---|
| Class | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | Spatial-Spectral FFPNet | Spatial-Spectral FFPNet + Data Enhancement | |
| Asphalt | 66.14 | 91.37 | 78.03 | 90.83 | 93.54 | 97.16 | 92.28 | 88.17 | |
| Meadows | 87.47 | 89.94 | 92.86 | 98.07 | 97.68 | 98.33 | 97.45 | 97.73 | |
| Gravel | 49.62 | 72.90 | 91.03 | 88.17 | 89.12 | 91.22 | 93.32 | 96.95 | |
| Trees | 57.44 | 84.73 | 59.79 | 90.08 | 72.19 | 81.07 | 83.16 | 90.73 | |
| Painted metal sheets | 95.24 | 96.73 | 97.92 | 98.81 | 98.51 | 99.40 | 96.13 | 98.21 | |
| Bare Soil | 18.46 | 85.28 | 60.14 | 99.28 | 94.99 | 97.69 | 95.78 | 98.81 | |
| Bitumen | 94.88 | 92.47 | 98.49 | 99.70 | 97.59 | 100.00 | 97.59 | 100.00 | |
| Self-Blocking Bricks | 36.96 | 80.00 | 36.74 | 87.72 | 77.39 | 91.74 | 71.09 | 94.35 | |
| Shadows | 79.65 | 93.81 | 79.65 | 92.48 | 93.36 | 97.79 | 95.13 | 96.02 | |
| OA | 67.99 | 87.92 | 79.47 | 95.09 | 92.66 | 95.99 | 92.87 | 95.59 | |
| AA | 65.09 | 87.47 | 77.18 | 93.90 | 90.49 | 94.93 | 91.33 | 95.66 | |
| Kappa | 56.52 | 84.19 | 72.73 | 93.52 | 90.24 | 94.68 | 90.55 | 94.19 | |
| Sample Patch Size | d = 9 | d = 15 | d = 19 | d = 29 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Models | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet |
| Alfalfa | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 95.65 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Corn-notill | 92.77 | 81.10 | 95.63 | 93.07 | 95.48 | 94.65 | 99.47 | 96.39 | 99.32 | 98.04 | 99.72 | 99.72 |
| Corn-mintill | 96.30 | 95.75 | 98.63 | 92.74 | 96.30 | 97.40 | 96.71 | 97.53 | 96.30 | 99.52 | 100.00 | 100.00 |
| Corn | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Grass-pasture | 96.61 | 98.43 | 98.96 | 97.13 | 97.13 | 99.48 | 97.91 | 95.82 | 97.65 | 94.17 | 96.67 | 98.33 |
| Grass-trees | 95.87 | 97.94 | 98.10 | 97.78 | 95.56 | 99.84 | 98.10 | 99.52 | 99.05 | 98.90 | 97.80 | 98.35 |
| Grass-pasture-mowed | 57.14 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Hay-windrowed | 99.74 | 98.94 | 100.00 | 98.41 | 99.47 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Oats | 100.00 | 90.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Soybeans-notill | 90.09 | 86.87 | 94.01 | 96.43 | 95.28 | 99.19 | 97.70 | 96.31 | 97.81 | 98.26 | 98.26 | 98.70 |
| Soybeans-mintill | 87.90 | 81.44 | 93.25 | 95.16 | 91.00 | 93.25 | 95.54 | 95.12 | 97.54 | 98.04 | 96.90 | 96.41 |
| Soybean-clean | 95.94 | 96.55 | 99.19 | 96.15 | 97.77 | 98.58 | 99.19 | 96.75 | 98.99 | 97.30 | 100.00 | 99.32 |
| Wheat | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Woods | 95.71 | 95.62 | 97.94 | 98.28 | 98.45 | 98.63 | 99.91 | 99.48 | 99.91 | 100.00 | 100.00 | 100.00 |
| Bldg-grass-tree-drives | 99.30 | 96.50 | 97.20 | 96.50 | 97.20 | 97.90 | 100.00 | 100.00 | 100.00 | 100.00 | 98.96 | 100.00 |
| Stone-steel towers | 97.87 | 95.74 | 100.00 | 97.87 | 95.74 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| OA | 93.15 | 89.53 | 96.30 | 95.86 | 95.31 | 96.78 | 97.97 | 97.16 | 98.50 | 98.55 | 98.70 | 98.74 |
| AA | 94.08 | 94.68 | 98.31 | 97.47 | 97.46 | 98.68 | 98.76 | 98.56 | 99.16 | 99.01 | 99.27 | 99.43 |
| Kappa | 92.10 | 87.95 | 95.73 | 95.20 | 94.58 | 96.29 | 97.65 | 96.72 | 98.27 | 98.34 | 98.52 | 98.57 |
| Run time | 13.37 | 5.80 | 15.13 | 15.88 | 8.68 | 17.86 | 14.42 | 8.48 | 14.66 | 16.67 | 16.01 | 21.57 |
| Sample Patch Size | d = 9 | d = 15 | d = 21 | d = 27 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Models | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet | Spatial FFPNet | Spectral FFPNet | Spatial-Spectral FFPNet |
| Asphalt | 79.48 | 57.82 | 88.65 | 90.04 | 81.41 | 94.57 | 91.43 | 94.39 | 97.34 | 88.47 | 84.67 | 91.61 |
| Meadows | 84.34 | 62.46 | 94.64 | 95.35 | 96.42 | 97.98 | 98.01 | 97.81 | 99.81 | 98.26 | 95.92 | 99.31 |
| Gravel | 76.91 | 68.70 | 90.27 | 90.27 | 91.79 | 96.37 | 98.09 | 94.47 | 98.09 | 97.90 | 97.52 | 98.66 |
| Trees | 76.89 | 54.44 | 86.03 | 80.68 | 78.98 | 92.95 | 87.60 | 69.84 | 94.39 | 93.08 | 83.29 | 93.34 |
| Painted metal sheets | 97.62 | 93.45 | 97.62 | 94.35 | 97.92 | 98.81 | 99.11 | 96.73 | 98.51 | 99.40 | 98.51 | 99.40 |
| Bare SoilC | 60.78 | 29.91 | 87.59 | 90.06 | 89.58 | 98.41 | 99.92 | 99.12 | 99.68 | 99.68 | 99.84 | 100.00 |
| Bitumen | 94.58 | 96.08 | 98.49 | 97.89 | 97.89 | 98.80 | 99.40 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 |
| Self-Blocking Bricks | 63.15 | 37.28 | 84.46 | 86.30 | 64.13 | 90.00 | 88.70 | 84.67 | 99.24 | 85.65 | 87.61 | 93.91 |
| Shadows | 91.59 | 91.59 | 93.81 | 92.48 | 91.59 | 97.35 | 97.35 | 97.35 | 98.23 | 97.35 | 93.36 | 99.12 |
| OA | 78.98 | 58.11 | 91.37 | 91.81 | 89.02 | 96.41 | 95.73 | 94.16 | 98.82 | 95.51 | 93.25 | 97.29 |
| AA | 80.59 | 65.75 | 91.28 | 90.82 | 87.75 | 96.14 | 95.51 | 92.71 | 98.37 | 95.53 | 93.41 | 97.26 |
| Kappa | 72.42 | 47.10 | 88.60 | 89.23 | 85.50 | 95.25 | 94.37 | 92.22 | 98.44 | 94.07 | 91.09 | 96.42 |
| Run time | 5.83 | 2.24 | 9.12 | 5.04 | 3.12 | 7.06 | 6.57 | 3.39 | 8.16 | 7.63 | 4.97 | 9.60 |
| CNN Models | Attention Networks [45] | Multiple CNN Fusion [42] | CNNs [41] | CNN [40] | Spatial-Spectral FFPNet | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A-ResNet | Samples | SODFN | FCLFN | Samples | 1-D | 2-D | 3-D | d = 9 | d = 19 | d = 29 | Samples | d = 9 | d = 19 | d = 29 | Samples | d = 9 | d = 15 | d = 19 | d = 29 | Samples | |
| Alfalfa | 89.23 | 7 | 95.12 | 95.12 | 5 | 89.58 | 99.65 | 100.00 | 100.00 | 100.00 | 100.00 | 30 | 99.13 | 99.57 | 99.13 | 23 | 95.65 | 100.00 | 100.00 | 100.00 | 33 |
| Corn-notill | 97.69 | 214 | 98.91 | 99.38 | 143 | 85.68 | 90.64 | 96.34 | 90.57 | 94.06 | 97.17 | 150 | 80.48 | 94.47 | 98.17 | 200 | 98.78 | 99.35 | 99.59 | 100.00 | 200 |
| Corn-min | 99.29 | 125 | 99.06 | 100.00 | 83 | 87.36 | 99.11 | 99.49 | 97.69 | 96.43 | 98.17 | 150 | 96.65 | 98.22 | 98.92 | 200 | 99.84 | 98.25 | 99.05 | 100.00 | 200 |
| Corn | 92.24 | 36 | 98.12 | 100.00 | 24 | 93.33 | 100.00 | 100.00 | 99.92 | 100.00 | 100.00 | 100 | 99.66 | 100.00 | 100.00 | 118 | 100.00 | 100.00 | 100.00 | 100.00 | 181 |
| Grass/Pasture | 99.02 | 72 | 95.62 | 95.16 | 49 | 96.88 | 98.48 | 99.91 | 98.10 | 98.72 | 98.76 | 150 | 99.46 | 99.75 | 99.71 | 200 | 100.00 | 100.00 | 98.94 | 100.00 | 200 |
| Grass/Trees | 99.77 | 110 | 99.09 | 99.24 | 73 | 98.99 | 97.95 | 99.75 | 99.34 | 99.67 | 100.00 | 150 | 99.53 | 98.90 | 99.40 | 200 | 99.62 | 100.00 | 98.87 | 100.00 | 200 |
| Grass/pasture-mowed | 93.04 | 4 | 80.03 | 72.10 | 3 | 91.67 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 20 | 100.00 | 100.00 | 100.00 | 14 | 100.00 | 100.00 | 100.00 | 100.00 | 20 |
| Hay-windrowed | 100.00 | 72 | 100.00 | 99.53 | 48 | 99.49 | 100.00 | 100.00 | 99.58 | 99.92 | 100.00 | 150 | 99.67 | 99.62 | 100.00 | 200 | 100.00 | 100.00 | 100.00 | 100.00 | 200 |
| Oats | 90.59 | 3 | 100.00 | 88.89 | 2 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 15 | 100.00 | 100.00 | 100.00 | 14 | 100.00 | 100.00 | 100.00 | 100.00 | 14 |
| Soybeans-notill | 98.57 | 146 | 99.31 | 99.54 | 98 | 90.35 | 95.33 | 98.72 | 94.28 | 97.63 | 99.14 | 150 | 92.43 | 98.00 | 98.62 | 200 | 99.33 | 99.73 | 100.00 | 100.00 | 200 |
| Soybeans-min | 99.37 | 368 | 98.87 | 98.64 | 245 | 77.90 | 78.21 | 95.52 | 87.75 | 92.93 | 94.59 | 150 | 76.42 | 94.32 | 96.15 | 200 | 98.58 | 99.38 | 99.78 | 99.35 | 200 |
| Soybean-clean | 97.14 | 89 | 87.99 | 92.68 | 60 | 95.82 | 99.39 | 99.47 | 94.81 | 97.17 | 99.06 | 150 | 97.74 | 99.09 | 99.33 | 200 | 99.24 | 100.00 | 100.00 | 100.00 | 200 |
| Wheat | 100.00 | 31 | 97.83 | 100.00 | 21 | 98.59 | 100.00 | 100.00 | 100.00 | 100.00 | 100.00 | 150 | 99.71 | 100.00 | 99.90 | 102 | 100.00 | 100.00 | 100.00 | 100.00 | 143 |
| Woods | 99.57 | 190 | 99.91 | 99.91 | 126 | 98.55 | 97.71 | 99.55 | 98.09 | 97.88 | 99.76 | 150 | 97.71 | 98.85 | 98.96 | 200 | 98.78 | 99.34 | 100.00 | 100.00 | 200 |
| Bldg-Grass-Tree-Drives | 99.58 | 58 | 98.56 | 97.41 | 39 | 87.41 | 99.31 | 99.54 | 89.79 | 95.80 | 98.39 | 50 | 99.27 | 99.90 | 100.00 | 193 | 100.00 | 100.00 | 100.00 | 100.00 | 200 |
| Stone-steel | 97.72 | 14 | 96.39 | 97.59 | 10 | 98.06 | 99.22 | 99.34 | 100.00 | 99.57 | 98.92 | 50 | 100.00 | 100.00 | 100.00 | 46 | 95.74 | 100.00 | 100.00 | 100.00 | 75 |
| OA | 98.75 | 98.21 | 98.56 | 87.81 | 89.99 | 97.56 | 93.94 | 96.29 | 97.87 | 90.11 | 97.23 | 98.37 | 99.07 | 99.47 | 99.68 | 99.84 | |||||
| AA | 97.05 | 96.54 | 95.94 | 93.12 | 97.19 | 99.23 | 96.87 | 98.11 | 99.00 | 96.12 | 98.79 | 99.27 | 99.10 | 99.75 | 99.76 | 99.96 | |||||
| Kappa | 98.58 | 97.97 | 98.36 | 85.30 | 87.95 | 97.02 | 93.12 | 95.78 | 97.57 | 88.81 | 96.85 | 98.15 | 98.90 | 99.38 | 99.63 | 99.82 | |||||
| Total samples | 1537 | 1029 | 1765 | 2466 | 2306 | ||||||||||||||||
| CNN Models | Attention Networks [45] | Multiple CNN Fusion [42] | CNNs [41] | CNN [40] | Spatial-Spectral FFPNet | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| A-ResNet | Samples | SODFN | FCLFN | Samples | 1-D | 2-D | 3-D | d = 15 | d = 21 | d = 27 | Samples | d = 15 | d = 21 | d = 27 | Samples | d = 9 | d = 15 | d = 21 | d = 27 | Samples | |
| Asphalt | 99.80 | 663 | 99.62 | 97.03 | 67 | 92.06 | 97.11 | 99.36 | 97.53 | 98.80 | 98.59 | 548 | 92.81 | 95.31 | 96.31 | 200 | 96.32 | 98.19 | 97.59 | 99.82 | 200 |
| Meadows | 99.97 | 1865 | 99.98 | 100.00 | 186 | 92.80 | 87.66 | 99.36 | 98.98 | 99.46 | 99.60 | 540 | 97.20 | 98.16 | 97.54 | 200 | 97.96 | 99.98 | 99.91 | 99.85 | 200 |
| Gravel | 99.56 | 210 | 97.47 | 95.14 | 22 | 83.67 | 99.69 | 99.69 | 98.96 | 99.59 | 99.45 | 392 | 96.97 | 97.92 | 96.84 | 200 | 95.99 | 98.66 | 99.81 | 99.05 | 200 |
| Trees | 99.74 | 306 | 91.79 | 88.49 | 31 | 93.85 | 98.49 | 99.63 | 99.75 | 99.68 | 99.57 | 542 | 98.62 | 98.74 | 97.58 | 200 | 90.60 | 96.61 | 96.34 | 96.61 | 200 |
| Painted metal sheets | 99.97 | 135 | 99.77 | 99.18 | 15 | 98.91 | 100.00 | 99.95 | 99.93 | 99.78 | 99.61 | 256 | 100.00 | 100.00 | 99.65 | 200 | 100.00 | 99.11 | 100.00 | 100.00 | 200 |
| Bare Soil | 100.00 | 503 | 96.77 | 99.46 | 51 | 94.17 | 98.00 | 99.96 | 99.42 | 99.93 | 99.84 | 532 | 98.57 | 99.57 | 99.33 | 200 | 93.95 | 100.00 | 100.00 | 100.00 | 200 |
| Bitumen | 99.16 | 133 | 89.51 | 95.89 | 15 | 92.68 | 99.89 | 100.00 | 98.71 | 99.88 | 100.00 | 375 | 97.27 | 99.75 | 98.90 | 200 | 97.59 | 100.00 | 100.00 | 100.00 | 200 |
| Self-Blocking Bricks | 99.73 | 368 | 97.59 | 100.00 | 38 | 89.09 | 99.70 | 99.65 | 98.58 | 99.53 | 99.67 | 514 | 96.17 | 98.20 | 98.89 | 200 | 96.30 | 99.02 | 98.04 | 99.13 | 200 |
| Shadows | 99.88 | 95 | 92.52 | 96.20 | 11 | 97.84 | 97.11 | 99.38 | 99.87 | 99.79 | 99.83 | 231 | 99.86 | 99.82 | 99.58 | 200 | 97.35 | 98.23 | 100.00 | 99.56 | 200 |
| OA | 99.86 | 98.13 | 98.17 | 92.28 | 94.04 | 99.54 | 98.87 | 99.47 | 99.48 | 96.83 | 98.06 | 97.80 | 96.51 | 99.25 | 99.15 | 99.53 | |||||
| AA | 99.76 | 96.11 | 96.80 | 92.55 | 97.52 | 99.66 | 99.08 | 99.60 | 99.57 | 97.50 | 98.61 | 98.29 | 96.23 | 98.87 | 99.08 | 99.33 | |||||
| Kappa | 99.82 | 97.53 | 97.58 | 90.37 | 92.43 | 99.41 | 98.51 | 99.30 | 99.32 | 95.83 | 97.44 | 97.09 | 95.37 | 99.01 | 98.87 | 99.38 | |||||
| Total samples | 4278 | 436 | 3930 | 1800 | 1800 | ||||||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Q.; Yuan, X.; Ouyang, C.; Zeng, Y. Attention-Based Pyramid Network for Segmentation and Classification of High-Resolution and Hyperspectral Remote Sensing Images. Remote Sens. 2020, 12, 3501. https://doi.org/10.3390/rs12213501
Xu Q, Yuan X, Ouyang C, Zeng Y. Attention-Based Pyramid Network for Segmentation and Classification of High-Resolution and Hyperspectral Remote Sensing Images. Remote Sensing. 2020; 12(21):3501. https://doi.org/10.3390/rs12213501
Chicago/Turabian StyleXu, Qingsong, Xin Yuan, Chaojun Ouyang, and Yue Zeng. 2020. "Attention-Based Pyramid Network for Segmentation and Classification of High-Resolution and Hyperspectral Remote Sensing Images" Remote Sensing 12, no. 21: 3501. https://doi.org/10.3390/rs12213501
APA StyleXu, Q., Yuan, X., Ouyang, C., & Zeng, Y. (2020). Attention-Based Pyramid Network for Segmentation and Classification of High-Resolution and Hyperspectral Remote Sensing Images. Remote Sensing, 12(21), 3501. https://doi.org/10.3390/rs12213501