Hyperspectral Anomaly Detection via Graph Dictionary-Based Low Rank Decomposition with Texture Feature Extraction
Abstract
:1. Introduction
- (1)
- A low-rank decomposition model with a novel graph-based dictionary is proposed. We construct the background dictionary through the graph Laplacian matrix incorporating with graph Fourier transform. It takes advantages of spatial connectivity and spectral correlation, and retains the major background components without calculating the high-dimensional covariance matrix and the inverse.
- (2)
- To the best of our knowledge, the texture features of HSIs are first utilized in anomaly detection. A texture feature-based LRD operation is designed to separate the sparse feature pixels and yield a feature map. It is fused with the original detection result of HSI to enhance the contrast between the background and the anomalies, and to make the detection result more accurate.
- (3)
- Making full use of the sparse property of anomalous targets and the spectral difference between anomalies and backgrounds, we propose to distinguish the targets both spatially and spectrally.
2. Proposed Method
2.1. Low Rank Decomposition Model for Anomaly Detection
2.2. Dictionary Construction Based on Graph Laplacian Matrix
2.3. Weight Selection of the Graph Model
2.4. Texture Features Extraction for Single Subspace LRD
- (i)
- Second moment:
- (ii)
- Contrast:
- (iii)
- Entropy:
- (iv)
- Correlation:
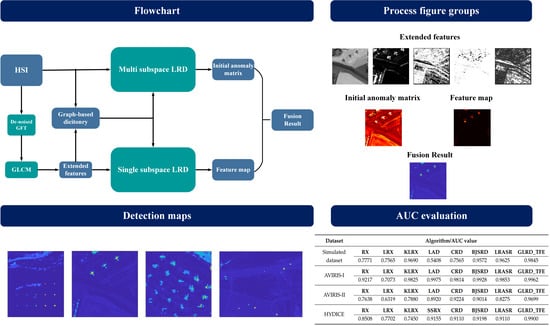
| Algorithm 1. Anomaly detection via graph dictionary-based LRD with texture feature extraction |
| 1: Input: hyperspectral image X; parameters: , , , , and . |
| 2.1: Obtain the weight matrix W by |
| where , |
| 2.2: L = D − W, D is calculated by (5). Then . |
| 2.3: Construct the graph-based background dictionary D by Equation (10). |
| 3: Solve the objective function of the multi-subspace LRD using LADMAP: |
| Obtain the sparse matrix . |
| 4: Calculate the de-noised version of GFT . Generate the GLCM of with |
| four texture features , and obtaining the extended feature . |
| 5: Solve the objective function of the single subspace LRD using soft threshold method in [34]: |
| Obtain the sparse matrix . |
| 6: Fuse two sparse matrices by weighted average-based method: |
| 7: Output: Final detection result Re. |
3. Experimental Results and Analysis
3.1. HSI Dataset Descriptions
3.2. Detection Performance
4. Parameter Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Stein, D.W.; Beaven, S.G.; Hoff, L.E.; Winter, E.M.; Schaum, A.P.; Stocker, A.D. Anomaly detection from hyperspectral imagery. IEEE Signal Proc. Mag. 2002, 19, 58–69. [Google Scholar] [CrossRef] [Green Version]
- Goetz, A.F.; Vane, G.; Solomon, J.E.; Rock, B.N. Imaging Spectrometry for Earth Remote Sensing. Science 1985, 228, 1147–1153. [Google Scholar] [CrossRef] [PubMed]
- Du, B.; Zhang, L. Random-selection-based anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2011, 49, 1578–1589. [Google Scholar] [CrossRef]
- Khazai, S.; Safari, A.; Mojaradi, B.; Homayouni, S. An approach for subpixel anomaly detection in hyperspectral images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2013, 6, 769–778. [Google Scholar] [CrossRef]
- Reed, I.S.; Yu, X. Adaptive multiple-band CFAR detection of an optical pattern with unknown spectral distribution. IEEE Trans. Acoust. Speech Signal Process. 1990, 38, 1760–1770. [Google Scholar] [CrossRef]
- Chen, J.Y.; Reed, I.S. A detection algorithm for optical targets in clutter. IEEE Trans. Aerosp. Electron. Syst. 1987, 23, 46–59. [Google Scholar] [CrossRef]
- Kwon, H.; Nasrabadi, N.M. Kernel RX-algorithm: A nonlinear anomaly detector for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2005, 43, 388–397. [Google Scholar] [CrossRef]
- Wright, J.; Yang, A.Y.; Ganesh, A.; Sastry, S.S.; Ma, Y. Robust face recognition via sparse representation. IEEE Trans. Pattern Anal. Mach. Intell. 2009, 31, 210–227. [Google Scholar] [CrossRef] [Green Version]
- Yang, J.; Wright, J.; Huang, T.; Ma, Y. Image super-resolution as sparse representation of raw image patches. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Anchorage, AK, USA, 23–28 June 2008; pp. 1–8. [Google Scholar]
- Chen, Y.; Nasrabadi, N.M.; Tran, T.D. Sparse representation for target detection in hyperspectral imagery. IEEE J. Sel. Top. Signal Process. 2011, 5, 629–640. [Google Scholar] [CrossRef]
- Li, W.; Du, Q. Collaborative representation for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2014, 53, 1463–1474. [Google Scholar] [CrossRef]
- Li, J.; Zhang, H.; Zhang, L.; Ma, L. Hyperspectral anomaly detection by the use of background joint sparse representation. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 2523–2533. [Google Scholar] [CrossRef]
- Sun, W.; Liu, C.; Li, J.; Lai, Y.M.; Li, W. Low-rank and sparse matrix decomposition-based anomaly detection for hyperspectral imagery. J. Appl. Remote. Sens. 2014, 8, 083641. [Google Scholar] [CrossRef]
- Zhang, Y.; Du, B.; Zhang, L.; Wang, S. A low-rank and sparse matrix decomposition-based mahalanobis distance method for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2015, 54, 1376–1389. [Google Scholar] [CrossRef]
- Xu, Y.; Wu, Z.; Li, J.; Plaza, A.; Wei, Z. Anomaly detection in hyperspectral images based on low-rank and sparse representation. IEEE Trans. Geosci. Remote Sens. 2016, 54, 1990–2000. [Google Scholar] [CrossRef]
- Liu, G.; Lin, Z.; Yan, S.; Sun, J.; Yu, Y.; Ma, Y. Robust recovery of subspace structures by low-rank representation. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 171–184. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Song, S.; Zhou, H.; Gu, L.; Yang, Y.; Yang, Y. Hyperspectral Anomaly Detection via Tensor-Based Endmember Extraction and Low-Rank Decomposition. IEEE Geosci. Remote. Sens. Lett. 2019, 17, 1772–1776. [Google Scholar] [CrossRef]
- Qu, Y.; Wang, W.; Guo, R.; Ayhan, B.; Kwan, C.; Vance, S.; Qi, H. Hyperspectral anomaly detection through spectral unmixing and dictionary-based low-rank decomposition. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4391–4405. [Google Scholar] [CrossRef]
- Li, F.; Zhang, X.; Zhang, L.; Jiang, D.; Zhang, Y. Exploiting structured sparsity for hyperspectral anomaly detection. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4050–4064. [Google Scholar] [CrossRef]
- Baterina, A.V.; Oppus, C. Image edge detection using ant colony optimization. WSEAS Trans. Signal Process. 2010, 6, 58–67. [Google Scholar]
- Mao, Q.; Wang, L.; Tsang, I.W.; Sun, Y. Principal graph and structure learning based on reversed graph embedding. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 395, 2227–2241. [Google Scholar] [CrossRef]
- Barnes, J.A.; Harary, F. Graph theory in network analysis. Soc. Netw. 1983, 5, 235–244. [Google Scholar] [CrossRef] [Green Version]
- Santner, J.; Pock, T.; Bischof, H. Interactive multi-label segmentation. In Asian Conference on Computer Vision, Proceedings of the ACCV 2010: Computer Vision, Queenstown, New Zealand, 8–12 November 2010; Springer: Berlin/Heidelberg, Germany, 2010; pp. 397–410. [Google Scholar]
- Akoglu, L.; Tong, H.; Koutra, D. Graph based anomaly detection and description: A survey. Data Min. Knowl. Discov. 2015, 29, 626–688. [Google Scholar] [CrossRef] [Green Version]
- Verdoja, F.; Grangetto, M. Graph Laplacian for image anomaly detection. Mach. Vis. Appl. 2020, 31, 11. [Google Scholar] [CrossRef] [Green Version]
- Zhao, R.; Zhang, L. GSEAD: Graphical scoring estimation for hyperspectral anomaly detection. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2016, 10, 725–739. [Google Scholar] [CrossRef]
- Yuan, Y.; Ma, D.; Wang, Q. Hyperspectral anomaly detection by graph pixel selection. IEEE Trans. Cybern. 2015, 46, 3123–3134. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.; Georganas, N.D.; Petriu, E.M. Fabric texture analysis using computer vision techniques. IEEE Trans. Instrum. Meas. 2010, 60, 44–56. [Google Scholar] [CrossRef]
- Malik, J.; Belongie, S.; Leung, T.; Shi, J. Contour and texture analysis for image segmentation. Int. J. Comput. Vis. 2001, 43, 7–27. [Google Scholar] [CrossRef]
- Kiechle, M.; Storath, M.; Weinmann, A.; Kleinsteuber, M. Model-based learning of local image features for unsupervised texture segmentation. IEEE Trans. Image Process. 2018, 27, 1994–2007. [Google Scholar] [CrossRef] [Green Version]
- Pla, F.; Gracia, G.; García-Sevilla, P.; Mirmehdi, M.; Xie, X. Multi-spectral texture characterisation for remote sensing image segmentation. In Iberian Conference on Pattern Recognition and Image Analysis, Proceedings of the IbPRIA 2009: Pattern Recognition and Image Analysis, Póvoa de Varzim, Portugal, 10–12 June 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 257–264. [Google Scholar]
- Liao, S.; Law, M.W.; Chung, A.C. Dominant local binary patterns for texture classification. IEEE Trans. Image Process. 2009, 18, 1107–1118. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Xi, B.; Li, Y.; Du, Q.; Wang, K. Hyperspectral classification based on texture feature enhancement and deep belief networks. Remote Sens. 2018, 10, 396. [Google Scholar] [CrossRef] [Green Version]
- Liu, G.; Lin, Z.; Yu, Y. Robust subspace segmentation by low-rank representation. In Proceedings of the 27th International Conference on Machine Learning (ICML-10), Haifa, Israel, 21–24 June 2010; pp. 663–670. [Google Scholar]
- Liu, G.; Yan, S. Latent low-rank representation for subspace segmentation and feature extraction. In Proceedings of the International Conference on Computer Vision (ICCV), Barcelona, Spain, 6–13 November 2011; pp. 1615–1622. [Google Scholar]
- Chung, F.R.; Graham, F.C. Spectral Graph Theory; American Mathematical Soc.: Providence, RI, USA, 1997; Volume 92, Available online: http://www.math.ucsd.edu/~fan/research/revised.html (accessed on 3 December 2020).
- Sandryhaila, A.; Moura, J.M. Discrete signal processing on graphs: Graph fourier transform. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, Canada, 26–31 May 2013; pp. 6167–6170. [Google Scholar]
- Chang, C.I.; Chiang, S.S. Anomaly detection and classification for hyperspectral imagery. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1314–1325. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Florêncio, D. Analyzing the optimality of predictive transform coding using graph-based models. IEEE Signal Process Lett. 2012, 20, 106–109. [Google Scholar] [CrossRef]
- Grady, L.J.; Polimeni, J.R. Applied Analysis on Graphs for Computational Science; Springer Science & Business Media: London, UK, 2010; Available online: https://www.springer.com/gp/book/9781849962896 (accessed on 3 December 2020).
- Black, M.J.; Sapiro, G.; Marimont, D.H.; Heeger, D. Robust anisotropic diffusion. IEEE Trans. Image Process. 1998, 7, 421–432. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Fracastoro, G.; Magli, E. Predictive graph construction for image compression. In Proceedings of the IEEE International Conference on Image Processing (ICIP), Quebec City, QC, Canada, 27–30 September 2015; pp. 2204–2208. [Google Scholar]
- Qian, Y.; Ye, M.; Zhou, J. Hyperspectral image classification based on structured sparse logistic regression and three-dimensional wavelet texture features. IEEE Trans. Geosci. Remote Sens. 2012, 51, 2276–2291. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Younan, N.H.; O’Hara, C.G. Wavelet domain statistical hyperspectral soil texture classification. IEEE Trans. Geosci. Remote Sens. 2005, 43, 615–618. [Google Scholar] [CrossRef]
- Faugeras, O.D.; Pratt, W.K. Decorrelation methods of texture feature extraction. IEEE Trans. Pattern Anal. Mach. Intell. 1980, 4, 323–332. [Google Scholar] [CrossRef]
- Soh, L.K.; Tsatsoulis, C. Texture analysis of SAR sea ice imagery using gray level co-occurrence matrices. IEEE Trans. Geosci. Remote Sens. 1999, 37, 780–795. [Google Scholar] [CrossRef] [Green Version]
- Sebastian, V.B.; Unnikrishnan, A.; Balakrishnan, K. Gray level co-occurrence matrices: Generalisation and some new features. arXiv 2012, arXiv:1205.4831. [Google Scholar]
- Partio, M.; Cramariuc, B.; Gabbouj, M.; Visa, A. Rock texture retrieval using gray level co-occurrence matrix. In Proceedings of the 5th Nordic Signal Processing Symposium, Bergen, Norway, 4–7 October 2002; Volume 75. [Google Scholar]
- De Siqueira, F.R.; Schwartz, W.R.; Pedrini, H. Multi-scale gray level co-occurrence matrices for texture description. Neurocomputing 2013, 120, 336–345. [Google Scholar] [CrossRef]
- Beura, S.; Majhi, B.; Dash, R. Mammogram classification using two dimensional discrete wavelet transform and gray-level co-occurrence matrix for detection of breast cancer. Neurocomputing 2015, 154, 1–14. [Google Scholar] [CrossRef]
- Haralick, R.M.; Shanmugam, K.; Dinstein, I.H. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 6, 610–621. [Google Scholar] [CrossRef] [Green Version]
- Kerekes, J. Receiver operating characteristic curve confidence intervals and regions. IEEE Geosci. Remote Sens. Lett. 2008, 5, 251–255. [Google Scholar] [CrossRef] [Green Version]
- Snyder, D.; Kerekes, J.; Fairweather, I.; Crabtree, R.; Shive, J.; Hager, S. Development of a web-based application to evaluate target finding algorithms. In Proceedings of the IGARSS 2008—2008 IEEE International Geoscience and Remote Sensing Symposium, Boston, MA, USA, 7–11 July 2008; Volume 2, pp. II-915–II-918. [Google Scholar]
- Stefanou, M.S.; Kerekes, J.P. A method for assessing spectral image utility. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1698–1706. [Google Scholar] [CrossRef]















| Dataset | Algorithm/AUC Value | |||||||
|---|---|---|---|---|---|---|---|---|
| Simulated dataset | RX | LRX | KLRX | LAD | CRD | BJSRD | LRASR | GLRD_TFE |
| 0.7771 | 0.7565 | 0.9690 | 0.5408 | 0.7565 | 0.9572 | 0.9625 | 0.9845 | |
| AVIRIS–I | RX | LRX | KLRX | LAD | CRD | BJSRD | LRASR | GLRD_TFE |
| 0.9217 | 0.7073 | 0.9825 | 0.9975 | 0.9814 | 0.9928 | 0.9853 | 0.9962 | |
| AVIRIS–II | RX | LRX | KLRX | LAD | CRD | BJSRD | LRASR | GLRD_TFE |
| 0.7638 | 0.6319 | 0.7880 | 0.8920 | 0.9224 | 0.9014 | 0.8275 | 0.9699 | |
| HYDICE | RX | LRX | KLRX | SSRX | CRD | BJSRD | LRASR | GLRD_TFE |
| 0.8508 | 0.7702 | 0.7450 | 0.9155 | 0.9110 | 0.9198 | 0.9110 | 0.9900 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, S.; Yang, Y.; Zhou, H.; Chan, J.C.-W. Hyperspectral Anomaly Detection via Graph Dictionary-Based Low Rank Decomposition with Texture Feature Extraction. Remote Sens. 2020, 12, 3966. https://doi.org/10.3390/rs12233966
Song S, Yang Y, Zhou H, Chan JC-W. Hyperspectral Anomaly Detection via Graph Dictionary-Based Low Rank Decomposition with Texture Feature Extraction. Remote Sensing. 2020; 12(23):3966. https://doi.org/10.3390/rs12233966
Chicago/Turabian StyleSong, Shangzhen, Yixin Yang, Huixin Zhou, and Jonathan Cheung-Wai Chan. 2020. "Hyperspectral Anomaly Detection via Graph Dictionary-Based Low Rank Decomposition with Texture Feature Extraction" Remote Sensing 12, no. 23: 3966. https://doi.org/10.3390/rs12233966
APA StyleSong, S., Yang, Y., Zhou, H., & Chan, J. C. -W. (2020). Hyperspectral Anomaly Detection via Graph Dictionary-Based Low Rank Decomposition with Texture Feature Extraction. Remote Sensing, 12(23), 3966. https://doi.org/10.3390/rs12233966